Simpson
の公式による数値積分1
H24
年度
BioS
継続勉強会:第7回補助資料1
土居 正明
1
はじめに
1.1
本稿の内容
本稿から、中間解析における棄却限界・検出力・例数を数値的に計算するための準備として、Simpsonの公式という数値 積分の方法をご紹介します。長くなりますので3つに分けまして、本稿では積分区間が有限、かつ、区間を均等に分割する 場合を扱います。さらに、積分する変数は1つとします。また、3稿とも通して、関数は全て常に0以上の値をとり、面積 はx軸との間で囲まれる部分について考えます。 アイデアは大変シンプルです。積分の基本である、「長方形で面積を近似する」方法に対して、「長方形の数が少ないとき に誤差が大きくなるので、2次関数を用いて近似精度を向上させる」だけです。1.2
前提とする公式
高校生の頃によく用いました、以下の公式を利用します。 Z β α (x − α)(x − β)dx = −(β − α) 3 6 (1)2
準備:長方形近似と台形近似
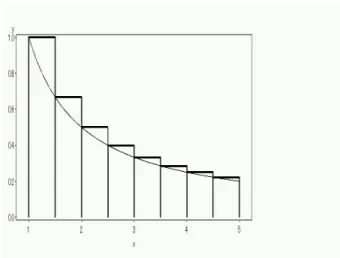
まずは簡単な例からです。高校数学の微分積分で「区分求積法」というのを考えました。これは大まかに言うと「面積を 長方形で近似して、長方形の幅を無限に小さくしていけば、正しい面積に収束する」というものでした*1。 ここで「収束する」とは、現実的には「長方形の幅を十分小さくしたら、近似精度が十分によくなる」ということです*2。 言葉で書くだけではイメージが沸かないかと思いますので、少しずつ幅を小さく(長方形の数を多く)して、近似が段々よ くなっていく様子を図で観察してみましょう。 なお、長方形などの足もとのx軸上の点 を「グリッド」と呼びます。 *1実は、厳密には話は逆で「ある種の極限がきちんとした値に収束する」ことが「(リーマン)積分可能」の定義で、高校までは概ね「『(リーマン)積 分可能』な関数だけを扱いましょう」という方針だったりするのですが、本稿や次稿・次々稿の範囲では気にされなくても結構です。厳密な話が気 になる方は、数学者の書かれた大学 1 年生レベルの微分積分の本にはほぼ間違いなく書いてありますので、読んでみてください。 *2「近似精度を先に指定してやれば、それに対応させて長方形の幅を適切に小さくしてやることで、求める精度範囲内で近似できる」(近似精度は正 の数である限り、どんな値をとってもよい)というのが、(名前だけは?)有名な「² − δ 論法(イプシロン・デルタろんぽう)」の今回の状況での解 釈です。抽象論をこねくり回しているだけではなくて、十分に実用上の問題意識がある、ということがお分かりいただければと思います。まあ、勉 強するときは抽象論をこねくり回すことになるのですが…。図1 y =x1 の長方形4個による近似 図2 y = 1xの長方形8個による近似 図3 y = 1xの長方形16個による近似 図4 y = 1 xの長方形32個による近似
2.1
長方形近似
上の4つの図は全てf (x) = 1 x としたときのy = f (x)のグラフです。図1では長方形4つで近似していますので、グ リッドはx = 1, 2, 3, 4, 5の5点となります。ここで、グリッド間の距離は常に1ですので、長方形の横幅は常に1です。一 方、縦は 左側のグリッド に対応するf (x)の値です。つまり、左端の長方形ではf (1) = 1、左から2個目ではf (2) =12、3 個目ではf (3) = 13、4個目ではf (4) = 14となります*3。これより、面積の近似値Sは S = f (1) · 1 + f (2) · 1 + f (3) · 1 + f (4) · 1 (2) と表せます*4。これを一般化させやすいように書き直しますと、 S = 3 X i=0 f (1 + 1 · i) · 1 となります。なお、1 · iの1はグリッドの間隔です。 次に、図2の場合です。今度は長方形8個で近似します。グリッドはx = 1,32, 2,52, 3,72, 4,92, 5です。グリッド幅は12 で あり、グリッドiでのf (x)の値はf (i)ですので、面積の近似値Sは以下のように書けます。 S = f (1) · 1 2+ f µ 3 2 ¶ ·1 2 + f (2) · 1 2 + f µ 5 2 ¶ ·1 2 + f (3) · 1 2 + f µ 7 2 ¶ · 1 2+ f (4) · 1 2+ f µ 9 2 ¶ ·1 2 *3このやり方で長方形近似する場合、右端のグリッドに対応する f (x) は用いませんのでご注意ください。 *4後で一般化させやすいように、f (1) ∼ f (4) は数値を代入しないままで扱います。まとめますと、長方形8個での近似は S = 7 X i=0 f µ 1 +1 2 · i ¶ ·1 2 となります。 ではこれを一般化させます。積分区間[a, b]での面積をn個の長方形に分けます(a, bは実数。∞は含みません。本稿で は以下同様です)。横幅を均等にしてグリッドの間隔をh = b − a n とおくと、面積の近似値Sは S = n−1 X i=0 f (a + h · i) · h (3) となります。本稿ではnを増やせば増やすほど近似精度がよくなり、 Z b a f (x)dx = lim n→∞h n−1X i=0 f (a + h · i) となる関数f (x)のみを考えます。数学・物理等一部の専門分野を除き、普通の人が無理せず考えつく関数は基本的にこの 関係を満たしています*5。例外として、積分区間の一部などで無限大に発散している関数、たとえばf (x) =√1 xを(0, 1)で 積分する場合などは、この方法がうまくいきません*6。また、工学でもよく出てきますDiracのdelta関数などは「超関数 (distribution)」で厳密には関数ではありませんので、それらの入った積分についてもうまくいかないことがあります。
2.2
台形近似
長方形近似(区分求積法)では、長方形の数を無限に増やせれば誤差は0になるのですが、現実的に無限個にすることは できません。また、数を増やせば増やすほど計算時間がかかるようになります。そこで、「少ないグリッド数で、もっと精 度の良い近似方法」があると嬉しそうです。以下、そのような近似方法を考えていきましょう。 さて、長方形近似では「横幅」と「左端のグリッドの大きさ」のみに影響を受ける長方形で近似しました。このとき、下 の図5 (図1と同じものです)の左端の長方形のように左右のグリッドでf (x)の値が大きく異なる場合に、誤差が大きくな るようです。そこで、右端のグリッドも利用 してやると、近似精度がよくなりそうです。このとき、最も簡単に思いつくの が「台形」で近似する方法でしょう。というわけで、以下、台形近似を考えていきます。まずは図で示します。 図5 y = 1 x の長方形近似(長方形4つ:図1と同じ) 図6 y = 1 xの台形近似(台形4つ) *5もう少し正確に言いますと、「右辺(をもう少し丁寧に考えたもの)がきちんと収束すること」が「f (x) がリーマン積分可能であること」の定義で、 そのときの極限で左辺を定義します。ですので、大体「左辺が適切に定義できる場合のみ扱います」ということです。 *6ちなみに、関数 √1 x は limx→0f (x) = ∞ となり、(0, 1) での積分の定義には一工夫必要です。このような積分を広義積分と呼びます。なお、 R1 0 dx √ x = 2 で積分は発散しません。近似精度が格段によくなっていることがお分かりいただけるかと思います。式で書くと、近似値Sは以下のようになり ます。 S =nf (1) + f (2)o· 1 ·1 2 + n f (2) + f (3)o· 1 ·1 2 + n f (3) + f (4)o· 1 · 1 2+ n f (4) + f (5)o· 1 ·1 2 = n−1X i=0 n f (1 + 1 · i) + f (1 + 1 · (i + 1))o·1 2 となります。なお、分子の「1」はグリッド幅(台形の高さ)です。グリッドを増やすと段々小さくなっていきます。これを 別の形にまとめますと、 S = n f (1) + f (2) o · 1 2+ n f (2) + f (3) o ·1 2 + n f (3) + f (4) o ·1 2 + n f (4) + f (5) o · 1 2 = f (1) ·1 2 + f (2) + f (3) + f (4) + f (5) · 1 2 = f (1) ·1 2 + 3 X i=1 f (1 + 1 · i) · 1 + f (5) ·1 2 となります。では、これを一般化させます。積分区間[a, b]をn個の台形に分け、グリッドの間隔をh = b − a n とおいたと き、グリッドは(n + 1)個で、面積の近似値Sは S = n−1X i=0 n f (a + h · i) + f (a + h · (i + 1))o·h 2 = n−1X i=0 f (a + h · i) ·h 2 + n−1 X i=0 f (a + h · (i + 1)) ·h 2 = n−1X i=0 f (a + h · i) ·h 2 + n X i=1 f (a + h · i) ·h 2 = f (a) ·h 2 + n−1 X i=1 f (a + h · i) · h + f (b) · h 2 = f (a) ·h 2 + n−1 X i=1 f (a + h · i) · h + f (b) · h 2 (4) となります。
3
Simpson
の公式
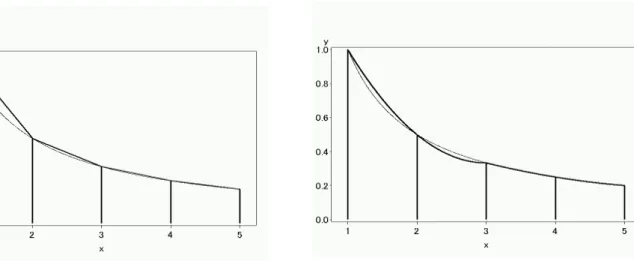
台形でもだいぶ精度が良さそうですが、さらに精度を上げる方法を考えましょう。台形で近似の悪い部分 は、大きく 曲がっている部分のようです。そこで、ここを曲線に変えるとさらに近似精度がよくなりそうな気がしてきます。で は、次に2次関数を用いて近似してみます。以下の図8では、グリッドx = 1, 2, 3の組とx = 3, 4, 5の組みに対して、 「(1, f (1)), (2, f (2)), (3, f (3))を通る2次関数」「(3, f (3)), (4, f (4)), (5, f (5))を通る2次関数」の2つで近似しています。 比較対象として、台形近似を持ってきますと、以下のようになります。図7 y = 1 x の台形近似(図6と同じ) 図8 y = 1 xの2次関数を用いた近似 台形の近似が悪くないのでそれほど顕著ではありませんが、それでもさらに近似精度が良くなったように見えます。この ように、2次関数で近似して面積を求める公式 を「Simpsonの公式」と呼びます。なお、長方形・台形の近似ではグリッド2 つで図形1つを構成していましたが、Simpsonの公式では グリッド3つで図形1つ を構成しますので、ご注意ください*7。
3.1
準備:
Lagrange
の補間公式(
2
次関数の場合)
Simpsonの公式を導出する準備として、Lagrangeの補間公式(2次関数の場合)をご紹介します。 【補題1:Lagrangeの補間公式(2次関数の場合)】 y = f (x)が3点(x1, y1), (x2, y2), (x3, y3)(ただし、x1, x2, x3は互いに異なる)を通るような2次 以下 の関数*8f (x)は 以下の式で与えられる。 f (x) = (x − x2)(x − x3) (x1− x2)(x1− x3) y1+ (x − x1)(x − x3) (x2− x1)(x2− x3) y2+ (x − x1)(x − x2) (x3− x1)(x3− x2) y3 【証明:補題1】 まず、f (x)が2次以下の関数であることは見れば明らかです*9。3点(x1, y1), (x2, y2), (x3, y3)を通ることは、代入して みれば分かります。実際代入してみますと、 f (x1) =(x1− x2)(x1− x3) (x1− x2)(x1− x3)y1+ (x1− x1)(x1− x3) (x2− x1)(x2− x3)y2+ (x1− x1)(x1− x2) (x3− x1)(x3− x2)y3= y1 f (x2) =(x2− x2)(x2− x3) (x1− x2)(x1− x3)y1+ (x2− x1)(x2− x3) (x2− x1)(x2− x3)y2+ (x2− x1)(x2− x2) (x3− x1)(x3− x2)y3= y2 f (x3) =(x3− x2)(x3− x3) (x1− x2)(x1− x3)y1+ (x3− x1)(x3− x3) (x2− x1)(x2− x3)y2+ (x3− x1)(x3− x2) (x3− x1)(x3− x2)y3= y3 より、確認できました*10。 (証明終わり) *72 次関数 f (x) = ax2+ bx + c には未知数が a, b, c の 3 つ存在しますので、データが 3 つなければ関数が 1 つに決まりません。 *8厳密には「(実数係数の)2 次以下の多項式」です。 *9明らかでない人は、通分した後、分子のカッコを展開して、x でまとめて確認してください。 *10厳密には、「上記の条件を満たす 3 点を通る 2 次以下の関数は一意的である(1 つしかない)」ことも証明する必要がありますが、本稿の議論の水準 を超えます(し、煩雑になります)ので省略します。3.1.1 Lagrangeの補間公式の具体例 簡単な具体例を2つご紹介します。 【例題1】 y = f (x)が3点(1, 2), (−2, 4), (3, 5)を通るような2次以下の関数f (x)を求めよ。 【解答:例題1】 (x1, y1) = (1, 2), (x2, y2) = (−2, 4), (x3, y3) = (3, 5)とおくと、Lagrangeの補間公式より f (x) = {x − (−2)} · (x − 3) {1 − (−2)} · (1 − 3) · 2 + (x − 1)(x − 3) {(−2) − 1} · {(−2) − 3}· 4 + (x − 1){x − (−2)} (3 − 1){3 − (−2)} ·5 = −(x + 2)(x − 3) 3 + 4(x − 1)(x − 3) 15 + (x − 1)(x + 2) 2 = −10(x 2− x − 6) + 8(x2− 4x + 3) + 15(x2+ x − 2) 30 = −10x 2+ 10x + 60 + 8x2− 32x + 24 + 15x2+ 15x − 30 30 = 13x2− 7x + 54 30 となります。念のため確認してみますと、 f (1) = 13 − 7 + 54 30 = 2, f (−2) = 52 + 14 + 54 30 = 4, f (3) = 117 − 21 + 54 30 = 5 となり、y = f (x)は確かに(1, 2), (−2, 4), (3, 5)を通っています。図で確認しておきますと、以下の通りです。 図9 3点を通る2次関数y =13x 2− 7x + 54 30 のグラフ 【例題2】 y = f (x)が3点(1, 3), (2, 5), (4, 9)を通るような2次以下の関数f (x)を求めよ。 【解答:例題2】 (x1, y1) = (1, 3), (x2, y2) = (2, 5), (x3, y3) = (4, 9)とおくと、Lagrangeの補間公式より f (x) = (x − 2)(x − 4) (1 − 2)(1 − 4) · 3 + (x − 1)(x − 4) (2 − 1)(2 − 4) · 5 + (x − 1)(x − 2) (4 − 1)(4 − 2) · 9
= 3(x − 2)(x − 4) 3 + 5(x − 1)(x − 4) −2 + 9(x − 1)(x − 2) 6 = 2(x 2− 6x + 8) + 5(x2− 5x + 4) + 3(x2− 3x + 2) 2 = 2x 2− 12x + 16 + 5x2− 25x + 20 + 3x2− 9x + 6 2 = 2x + 1 となります。念のため確認してみますと、f (1) = 3, f (2) = 5, f (4) = 9となり、確かに(1, 3), (2, 5), (4, 9)を通っています。 このように、3点が1直線上に並んでいるときには、きちんと1次関数が出てきてくれます*11。これも図で確認しておきま すと、以下の通りです。 図10 3点を通る直線y = 2x + 1のグラフ
3.2
Simpson
の公式
最初にも書きました通り、Simpsonの公式 とは、面積を2次関数で近似して求める方法です。実際に計算する際、2次関 数の導出にLagrangeの補間公式を用います。 【定理1:Simpsonの公式】 3点(x1, y1), (x2, y2), (x3, y3)に対して、x1< x2< x3かつx3− x2= x2− x1=d 2 とする*12。このとき、y = f (x)が この3点を通るような2次以下の関数f (x)をx1からx3まで積分した値をSとおくと、 S = d 6y1+ 4d 6 y2+ d 6y3 (5) となる。 【証明:定理1】 いま、x1, x2, x3が互いに異なるので、3点(x1, y1), (x2, y2), (x3, y3)を通る2次関数f (x)はLagrangeの補間公式より f (x) = (x − x2)(x − x3) (x1− x2)(x1− x3)y1+ (x − x1)(x − x3) (x2− x1)(x2− x3)y2+ (x − x1)(x − x2) (x3− x1)(x3− x2)y3 *112 次 以下 と書き続けていたのはこのためです。なお、「補題 1」で証明を省略しました「3 点を通る 2 次以下の関数は一意的である」ことを使用し ますと、「一直線上に並んだ 3 点を通る 2 次関数は存在しない」ことが分かります。 *12「3 つ組のグリッドのうち、真ん中のグリッドは左右のグリッドの中点にある」ことが重要です。で与えられます。これより、この関数をx1からx3まで積分すれば、Sが求まります。つまり、 S = Z x3 x1 f (x)dx = Z x3 x1 ½ (x − x2)(x − x3) (x1− x2)(x1− x3)y1+ (x − x1)(x − x3) (x2− x1)(x2− x3)y2+ (x − x1)(x − x2) (x3− x1)(x3− x2)y3 ¾ dx となります。少し整理すると、 S = y1 (x1− x2)(x1− x3) Z x3 x1 (x − x2)(x − x3)dx + y2 (x2− x1)(x2− x3) Z x3 x1 (x − x1)(x − x3)dx + y3 (x3− x1)(x3− x2) Z x3 x1 (x − x1)(x − x2)dx (6) となります。ここで、積分の部分のみ取り出して計算してやります*13。まず最初の積分は Z x3 x1 (x − x2)(x − x3)dx = Z x3 x1 n (x − x1) + (x1− x2) o (x − x3)dx = Z x3 x1 (x − x1)(x − x3)dx + (x1− x2) Z x3 x1 (x − x3)dx = −1 6(x3− x1) 3+ (x 1− x2) · 1 2(x − x3) 2 ¸x3 x1 = −1 6(x3− x1) 3+ (x 1− x2) ½ 0 − 1 2(x1− x3) 2 ¾ = −d 3 6 + µ −d 2 ¶ · µ −d 2 2 ¶ µ ∵ x3− x2= x2− x1= d 2, x3− x1= d ¶ = d 3 12 (7) となります。2番目の積分は(1)がそのまま使えて、 Z x3 x1 (x − x1)(x − x3)dx = − (x3− x1)3 6 = − d3 6 (8) です。最後に3番目の積分は、 Z x3 x1 (x − x1)(x − x2)dx = Z x3 x1 (x − x1){(x − x3) + (x3− x2)}dx = Z x3 x1 (x − x1)(x − x3)dx + (x3− x2) Z x3 x1 (x − x1)dx = −(x3− x1) 3 6 + (x3− x2) · (x − x1)2 2 ¸x3 x1 = −(x3− x1) 3 6 + (x3− x2) (x3− x1)2 2 = −d3 6 + d 2· d2 2 µ ∵ x3− x2= x2− x1= d 2 ¶ = d3 12 (9) *13 以下、式 (1) Z β α (x − α)(x − β)dx = − (β − α)3 6 をよく使います。一見使えなさそうな場合も、以下のように変形して使えるようにしてやります。 Zβ α (x − α)(x − γ)dx = Z β α (x − α) n (x − β) + (β − γ)odx = Zβ α (x − α)(x − β)dx + (β − γ) Zβ α (x − α)dx
となります。これより、(7)、(8)、(9)を(6)に代入すると、 S = y1 (x1− x2)(x1− x3) ·d3 12+ y2 (x2− x1)(x2− x3) · µ −d3 6 ¶ + y3 (x3− x1)(x3− x2) ·d3 12 = µ y1 −d 2 ¶ · (−d) ·d3 12+ y2 d 2 · µ −d 2 ¶ · µ −d3 6 ¶ + y3 d · d 2 · d3 12 µ ∵ x2− x1= x3− x2= d 2, x3− x1= d ¶ = d 6y1+ 4d 6 y2+ d 6y3 となります。 (証明終わり) では、具体例で確認しましょう。図8を再度載せておきますと、 図11 y =x1 の2次関数を用いた近似(図8と同じ) でした。この図の、1 ≤ x ≤ 3の部分をSimpsonの公式で近似した面積をSとおきます。(1, 1), (2,12), (3,13)の3点を通る 2次関数f (x)を考え、積分しますと、グリッドの間隔d2 = 1からd = 2で S = 2 6 · 1 + 4 · 2 6 · 1 2+ 2 6 · 1 3 = 20 18 = 10 9 ; 1.1111 となります。なお、理論値は Z 3 1 dx x = [log x] 3 1= log(3) − log(1) ; 1.0986 となり、グリッド3つにしてはだいぶよい近似精度となります。 3.2.1 まとめ Simpsonの公式の大変便利なところは、「式が簡単」なところです。Lagrangeの補間公式は、式の形も少々面倒ですし、 積分するのも少し大変だったかと思います。しかしSimpsonの公式の形にまとめてしまうと、大変シンプルな形になりま す。グリッドxiに対応するグラフのy座標yi= f (xi)の値とグリッド幅の2倍dを代入してやるだけです。これくらいで すと、計算ミス(プログラムミス)も起こりにくいでしょう。
3.3
Simpson
の公式の具体例
以下、3つの具体例に対して、長方形近似・台形近似・Simpsonの公式でそれぞれ数値積分していきます。【例1】 f (x) = 1 xを1 ≤ x ≤ 5で積分します。なお、h = 1, 0.1, 0.01, 0.001, 0.0001の5通りを考えます。 h = 1の場合のみ手計算 を行い、残りはSASで実行することにします。このとき、x1= 1, x2= 2, x3= 3, x4= 4, x5= 5 です。また、対応するyの値はy1= f (x1) = 11 = 1, y2= f (x2) = 12, y3= f (x3) = 13, y4= f (x4) = 14 です。度々繰り返 しになりますが、図を載せておきます。 図12 y = 1 xの長方形近似(長方形4つ:図1と同じ) 図13 y = 1 xの台形近似(台形4つ:図6と同じ) 図14 y = 1xの2次関数を用いた近似(2次関数2つ:図8と同じ) (i)長方形近似 Z 4 0 f (x)dx ; h · 4 X i=1 f (xi) = 1 · µ 1 + 1 2+ 1 3 + 1 4 ¶ = 25 12 = 2.0833 となります。
(ii)台形近似 Z 4 0 f (x)dx ; f (x1) · h 2 + h · 4 X i=2 f (xi) + f (x5) · h 2 = 1 ·1 2 + 1 · µ 1 2 + 1 3 + 1 4 ¶ +1 5 · 1 2 = 1.683333 (iii) Simpsonの公式 まずは左側からの3点(x1, y1), (x2, y2), (x3, y3)に対して、 S1= d 6y1+ 4d 6 y2+ d 6y3 となります。次に3点(x3, y3), (x4, y4), (x5, y5)に対して、 S2= d 6y3+ 4d 6 y4+ d 6y5 となります。これより、面積の合計は S = S1+ S2= µ d 6y1+ 4d 6 y2+ d 6y3 ¶ + µ d 6y3+ 4d 6 y4+ d 6y5 ¶ = d 6y1+ 4d 6 y2+ 2d 6 y3+ 4d 6 y4+ d 6y5 = 2 6· 1 + 8 6 · 1 2 + 4 6 · 1 3 + 8 6· 1 4 + 2 6· 1 5 ; 1.62222 となります。y3がS1, S2の両方に登場していますので、きちんと2回数えてやりましょう。
3.4
Simpson
の公式のまとめ
上でy3が2回登場した 部分を精密に述べて、Simpsonの公式を用いた面積計算についてまとめておきましょう。ポイン トは • グリッドが奇数個必要 • 1番左端・1番右端のグリッド以外の、奇数番目のグリッドの部分は、2回ずつ計算に現れる (S1: {x1, x2, x3}, S2: {x3, x4, x5}) ということです。SASプログラムでマクロを作成するときには、以下の定理を用いることとします。【定理2:Simpsonの公式を用いた面積計算】 x1< x2< · · · < x2m< x2m+1とし、対応するf (xi)の値をyiとおく。また、xi+1− xi= d2 とする。このとき、 hi= d 6 (i = 1, 2m + 1) 4d 6 (i :偶数) 2d 6 (i : 1, 2m + 1以外の奇数) とおくと、Simpsonの公式を用いた面積の近似式Sは S = 2m+1X i=1 yihi (10) と表せる。 【証明:定理2】 足し算してやるだけです。 S1= d 6y1+ 4 6y2+ d 6y3 S2= d 6y3+ 4 6y4+ d 6y5 S3= d 6y5+ 4 6y6+ d 6y7 S4= d 6y7+ 4 6y8+ d 6y9 .. . Sn= d 6y2n−1+ 4 6y2n+ d 6y2n+1 より、 • y1とy2n+1の係数:d6 • y2, y4, · · · , y2nの係数:4d6 • y3, y5, · · · , y2n−1の係数:2d6 となります。 (証明終わり)
4
プログラム
では、以下、関数f (x)をマクロで与えたとき、「長方形近似」「台形近似」「Simpsonの公式」でそれぞれ面積の近似計算 を行うマクロを作ります。その際、グリッド数(グリッド間隔)を適宜変更していくことで、どのくらいのグリッド数のと きに近似精度がよくなるかをみていきます。 計算はデータステップでの計算が主となります。作成するデータセットのイメージは、グリッド数がnのとき、グリッド番号 グリッドのx座標 そこでの関数f (x)の値 関数f (x)にかける係数 f (x)と係数の積 合計 1 x1 f (x1) h1 h1· f (x1) h1· f (x1) 2 x2 f (x2) h2 h2· f (x2) P2 i=1 hi· f (xi) 3 x3 f (x3) h3 h3· f (x3) P3 i=1 hi· f (xi) .. . ... ... ... ... ... n − 1 xn−1 f (xn−1) hn−1 hn−1· f (xn−1) n−1P i=1 hi· f (xi) n xn f (xn) hn hn· f (xn) n P i=1 hi· f (xi) です。ここで、表の右下にある n X i=1 hi· f (xi) (11) が面積の近似値です*14。もう少し詳しく解説しますと、式(3)(4)(10)を使用しまして、例えばグリッドが5つx1< x2 < x3< x4< x5、グリッド幅hとしますと、長方形近似は S = h · f (x1) + h · f (x2) + h · f (x3) + h · f (x4) です。つまり、h1= h2= h3= h4= hとおくと、 S = 4 X i=1 hi· f (xi) と書けます。次に、台形近似は S = h 2 · f (x1) + h · f (x2) + h · f (x3) + h · f (x4) + h 2 · f (x5) です。つまり、h1= h5= h 2, h2= h3= h4= hとおくと、 S = 5 X i=1 hi· f (xi) と書けます。最後に、Simpsonの公式では、グリッド間隔をd2 とおきまして、 S = d 6 · f (x1) + 4d 6 · f (x2) + 2d 6 · f (x3) + 4d 6 · f (x4) + d 6 · f (x6) です。つまり、h1= h5=d 6, h2= h4= 4d 6 , h3= 2d 6 とおくと、 S = 5 X i=1 hi· f (xi) と書けます。この、足し算の項1つを、データセットの1行にしてやるのです。 *14長方形の場合は、右端のグリッドを利用しませんので n−1X i=1 f (xi) · hi となります。
では、これを用いて以下SASプログラムを作って計算していきましょう。変数の意味は以下の通りです*15。
n:グリッド数, step:グリッド間隔, start:積分区間の下限(左端のグリッド), end:積分区間の上限(右端のグリッド) no:通し番号
*長方形近似マクロ;
%macro rect(start, end, step, no);
data d1; no = &no;
n = (&end - &start) / &step + 1; *グリッド数; step = &step; *グリッド間隔;
do i=1 to (n-1); *右端のグリッドは使用しないため、「グリッド数−1」個の和; x = &start + (i-1) * &step; *グリッド;
f = %f(x); *縦; h = &step; *横; area + f * h; *長方形の面積の和; output; end; run;
data out1 &no;
length no 8. type $12.; set d1 end=final; type = ”rectangular”; if final then output; drop i x f h; run;
%mend rect; *台形近似マクロ;
%macro trape(start, end, step, no);
data d2; no = &no;
n = (&end - &start) / &step + 1; *グリッド数; step = &step; *グリッド間隔;
do i = 1 to n; *「グリッド数」個の和; x = &start + (i-1) * &step; *グリッド; f = %f(x); *上底または下底;
if i=1 or i=n then h= &step/2; *係数は左端と右端だけグリッド幅の半分; else h = &step; *それ以外はグリッド幅; area + f * h; *面積の和; output; end; run; *15なお、グリッド数は n (右端のグリッド)−(左端のグリッド) o ÷グリッド間隔 +1 で求まります。たとえば、4 ∼ 10 の間にグリッド幅 2 のグ リッドをとりますと、(10 − 4)/2 + 1 = 4 となります。1 つずつ数えると、4, 6, 8, 10 となり、確かに一致しています。
data out2 &no;
length no 8. type $10.; set d2 end=final; type = ”trapezoid”; if final then output; drop i x f h; run;
%mend trape;
*Simpsonの公式マクロ;
%macro simp(start, end, step, no);
data d3; no = &no;
n = (&end - &start) / &step + 1; *グリッド数; d = 2*&step; *グリッド間隔の2倍;
step = &step; *グリッド幅;
do i =1 to n; *「グリッド数」個の和; x = &start + (i-1)*d / 2; *グリッド; f = %f(x);
if i=1 or i=n then area + f * d / 6; *両端のグリッドのとき;
else if mod(i, 2) = 0 then area + f * 4 * d / 6; *偶数番目のグリッドのとき; else area + f * 2 * d / 6; *両端でない奇数番目のグリッドのとき;
output; end; run;
data out3 &no;
length no 8. type $10.; set d3 end=final; type = ”Simpson”; if final then output; drop i x f;
run; %mend simp;
次に、3つの計算法をまとめて実行するマクロを作成します。
%macro exe0(start, end, step, no);
%rect(&start, &end, &step, &no)
%trape(&start, &end, &step, &no)
%simp(&start, &end, &step, &no)
%mend exe0;
%macro exe(start, end, no);
%exe0(&start, &end, 1, &no)
%exe0(&start, &end, 0.1, %eval(&no + 1)) %exe0(&start, &end, 0.01, %eval(&no + 2))
%exe0(&start, &end, 0.001, %eval(&no + 3))
%exe0(&start, &end, 0.0001, %eval(&no + 4))
*長方形近似の結果のまとめ; data out rect &no;
set out1 &no out1 %eval(&no +1 ) out1 %eval(&no + 2) out1 %eval(&no + 3) out1 %eval(&no + 4); run;
*台形近似の結果のまとめ; data out trape &no;
set out2 &no out2 %eval(&no + 1) out2 %eval(&no + 2) out2 %eval(&no + 3) out2 %eval(&no + 4); run;
*Simpsonの公式を用いた近似の結果のまとめ; data out simp &no;
set out3 &no out3 %eval(&no + 1) out3 %eval(&no + 2) out3 %eval(&no + 3) out3 %eval(&no + 4); run; %mend exe; マクロの実行の前に、理論値を求めておいてやりましょう。 Z 5 1 1 xdx = h log(x) i5 1= log(5) より、 data check 1; area = log(5) ; run; で求まります。理論値の出力は以下のようになります。 表1 f (x) = x1 の1 ≤ x ≤ 5での積分の理論値 area 1.60944 では次に、近似計算マクロを実行します。まず、関数f (x)を指定してやります。 %macro f(x); 1 / &x %mend f;
実行プログラムは以下の通りです。
%exe(1, 5, 1)
出力は以下の通りです。以下、近似精度のよい部分を太字にします。
表2 f (x) = 1
xの1 ≤ x ≤ 5での積分の長方形近似
no type n step area
1 rectangular 5 1.0000 2.08333 2 rectangular 41 0.1000 1.65024 3 rectangular 401 0.0100 1.61345 4 rectangular 4001 0.0010 1.60984 5 rectangular 40001 0.0001 1.60948 表3 f (x) = 1 xの1 ≤ x ≤ 5での積分の台形近似
no type n step area
1 trapezoid 5 1.0000 1.68333 2 trapezoid 41 0.1000 1.61024 3 trapezoid 401 0.0100 1.60945 4 trapezoid 4001 0.0010 1.60944 5 trapezoid 40001 0.0001 1.60944 表4 f (x) = 1xの1 ≤ x ≤ 5での積分のSimpsonの公式を用いた近似
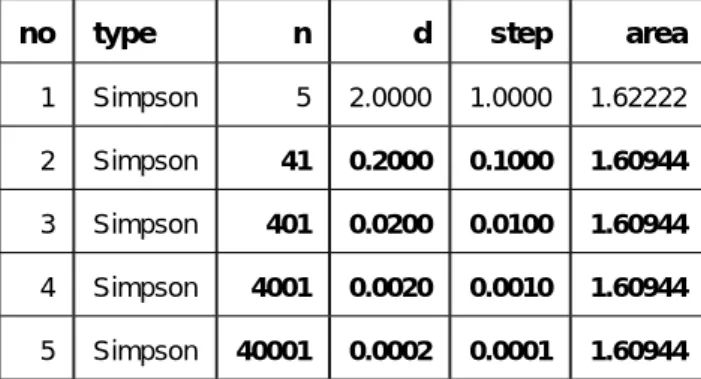
no type n d step area
1 Simpson 5 2.0000 1.0000 1.62222 2 Simpson 41 0.2000 0.1000 1.60944 3 Simpson 401 0.0200 0.0100 1.60944 4 Simpson 4001 0.0020 0.0010 1.60944 5 Simpson 40001 0.0002 0.0001 1.60944 以上より、狙い通り精度のよい順に「Simpsonの公式」「台形近似」「長方形近似」となりました。特にSimpsonの公式は、 n = 4でも理論値とそれほどずれていない、という結果になっています*16。 【例2】 f (x) = exp(x)を0 ≤ x ≤ 4で積分します。理論値は Z 4 0 f (x)dx = Z 4 0 exp(x)dx =hexp(x)i4 0= e 4− 1 から、 data check 2;
area = exp(4) - exp(0); run;
で求まります。理論値の出力は以下の通りです。
表5 f (x) = exp(x)の0 ≤ x ≤ 4での積分の理論値 area 53.5982 近似計算のプログラムは、関数f (x)の形のみ変更します。 %macro f(x); exp(&x) %mend f; 実行プログラムは以下の通りです。 %exe(0, 4, 11) 出力は以下の通りです。 表6 f (x) = exp(x)の0 ≤ x ≤ 4での積分の長方形近似
no type n step area
11 rectangular 5 1.0000 31.1929 12 rectangular 41 0.1000 50.9629 13 rectangular 401 0.0100 53.3306 14 rectangular 4001 0.0010 53.5714 15 rectangular 40001 0.0001 53.5955 表7 f (x) = 1 xの1 ≤ x ≤ 5での積分の台形近似
no type n step area
11 trapezoid 5 1.0000 57.9919 12 trapezoid 41 0.1000 53.6428 13 trapezoid 401 0.0100 53.5986 14 trapezoid 4001 0.0010 53.5982 15 trapezoid 40001 0.0001 53.5982 表8 f (x) = 1 x の1 ≤ x ≤ 5での積分のSimpsonの公式による近似
no type n d step area
11 Simpson 5 2.0000 1.0000 53.8638 12 Simpson 41 0.2000 0.1000 53.5982 13 Simpson 401 0.0200 0.0100 53.5982 14 Simpson 4001 0.0020 0.0010 53.5982 15 Simpson 40001 0.0002 0.0001 53.5982 やはりn = 4での近似が、Simpsonの公式のときに大変よくなり、n = 40で小数第4位まで理論値と一致します。
【例3】 f (x) = exp ³ −x2 2 ´ を−1 ≤ x ≤ 3で積分します。なお、h = 1, 0.1, 0.01, 0.001, 0.0001の5通りを考えます。まずは理 論値です。標準正規分布の確率密度関数に帰着させてやります。 Z 3 −1 exp µ −x 2 2 ¶ dx =√2π Z 3 −1 1 √ 2πexp µ −x 2 2 ¶ dx =√2π µZ 3 −∞ 1 √ 2πexp µ −x 2 2 ¶ dx − Z −1 −∞ 1 √ 2πexp µ −x 2 2 ¶ dx ¶ =√2π {Φ(3) − Φ(−1)} となります。これより、理論値は data check 2; pi = constant(’pi’); *変数piにπを代入します; area = sqrt(2 * pi) * (cdf(’norm’, 3) - cdf(’norm’, -1); run; で求まります。出力は以下の通りです。 表9 f (x) = exp “ −x2 2 ” の−1 ≤ x ≤ 3での積分の理論値 area 2.10555 近似計算のプログラムは、関数f (x)の形のみ変更します。 %macro f(x); exp(-1/2 * (&x**2)) %mend f; 実行プログラムは以下の通りです。 %exe(-1, 3, 21) 出力は3つを一覧で示すために、次のページで示します。
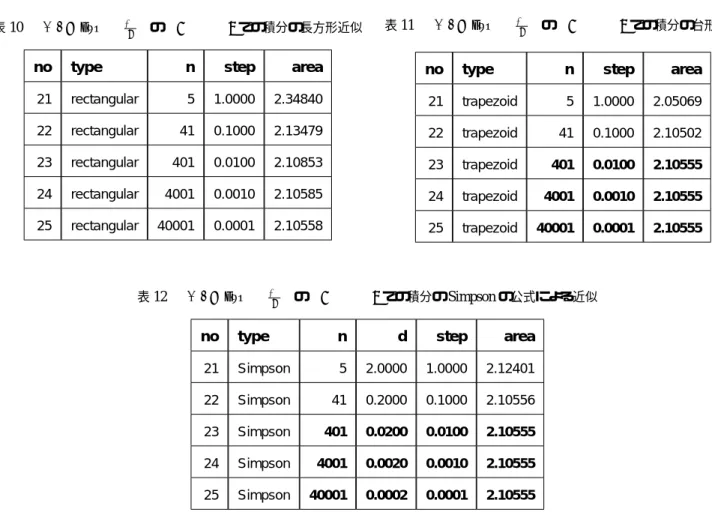
表10 f (x) = exp “ −x2 2 ” の−1 ≤ x ≤ 3での積分の長方形近似
no type n step area
21 rectangular 5 1.0000 2.34840 22 rectangular 41 0.1000 2.13479 23 rectangular 401 0.0100 2.10853 24 rectangular 4001 0.0010 2.10585 25 rectangular 40001 0.0001 2.10558 表11 f (x) = exp “ −x2 2 ” の−1 ≤ x ≤ 3での積分の台形近似
no type n step area
21 trapezoid 5 1.0000 2.05069 22 trapezoid 41 0.1000 2.10502 23 trapezoid 401 0.0100 2.10555 24 trapezoid 4001 0.0010 2.10555 25 trapezoid 40001 0.0001 2.10555 表12 f (x) = exp “ −x2 2 ” の−1 ≤ x ≤ 3での積分のSimpsonの公式による近似
no type n d step area
21 Simpson 5 2.0000 1.0000 2.12401 22 Simpson 41 0.2000 0.1000 2.10556 23 Simpson 401 0.0200 0.0100 2.10555 24 Simpson 4001 0.0020 0.0010 2.10555 25 Simpson 40001 0.0002 0.0001 2.10555 今回も、nが小さい場合でも、Simpsonの公式の近似精度が大変よいことがお分かりいただけたかと思います。
参考文献
[1] Jennison,C., and Turnbull,B,W. (1999) Group Sequential Methods with application to Clinical Trials. Chapman Hall/CRC. [2] 森川敏彦,山中竹春(2012)臨床試験における群逐次法 理論と応用,株式会社シーエーシー.([1]の和訳です)