つくばリポジトリ SR 8 1 988
全文
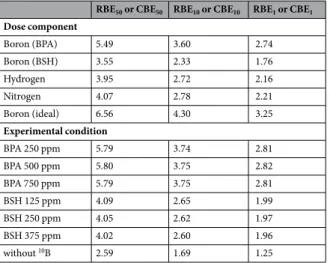
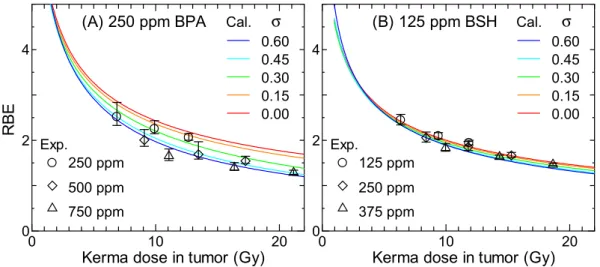
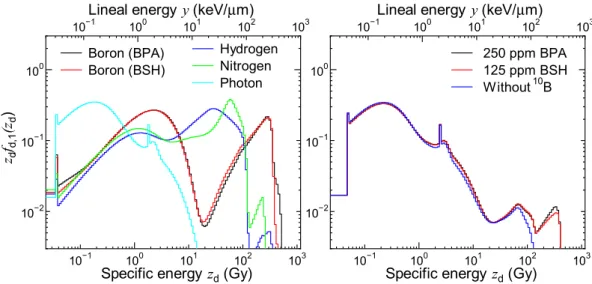
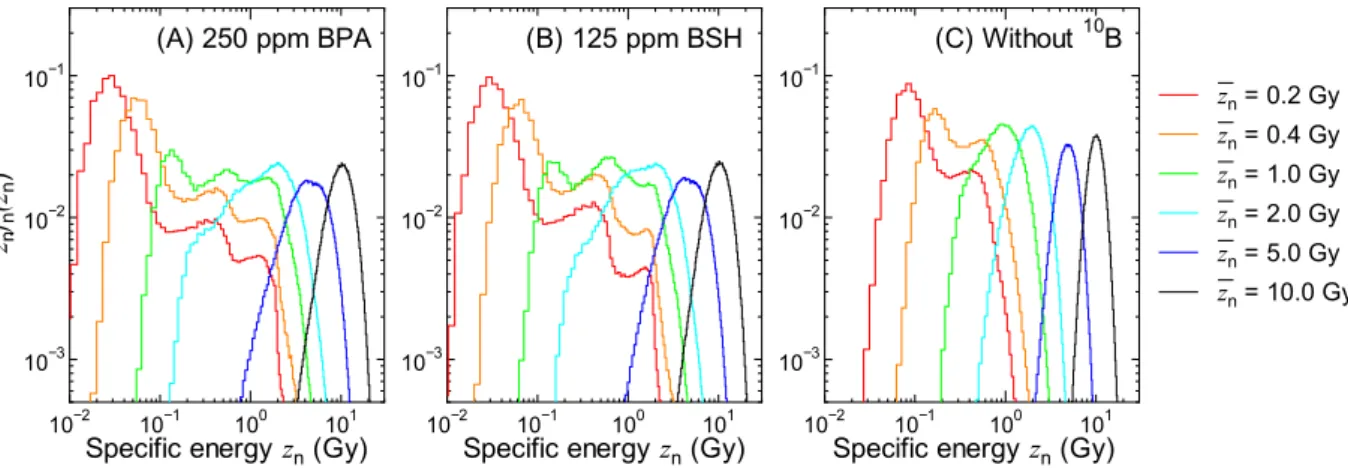
図
関連したドキュメント
In this paper, we present a new numerical scheme by QSC methods to solve the fractional bioheat equation with mixed boundary value conditions for thermal therapy.. This new
We derive rigorously a homogenized model for the displacement of one compressible miscible fluid by another in a partially fractured porous reservoir.. We denote by the
AHP involves three basic elements: (1) it describes a complex, multicriteria problem with objective or subjective elements as a hierarchy; (2) it estimates the relative weights
In this paper, for the first time an economic production quantity model for deteriorating items has been considered under inflation and time discounting over a stochastic time
Johns, “Asymptotic distribution of linear combinations of functions of order statistics with applications to estimation,” Annals of Mathematical Statistics, vol.. Hosking,
It is suggested by our method that most of the quadratic algebras for all St¨ ackel equivalence classes of 3D second order quantum superintegrable systems on conformally flat
[9] DiBenedetto, E.; Gianazza, U.; Vespri, V.; Harnack’s inequality for degenerate and singular parabolic equations, Springer Monographs in Mathematics, Springer, New York (2012),
Key words: Evolution family of bounded linear operators, evolution operator semigroup, Rolewicz’s theorem.. 2001 Southwest Texas