社会工学実習
経営工学分野 第1回
–
ビュッフォンの針で円周率を
–
担当:八森正泰・山本芳嗣・後藤順哉
1
ビュッフォンの針の問題の理論(1時間目)
図 1 のように針を等間隔に引かれた平行線上にでたらめに落として、針が平行線と交差するかどうかを 観測する。この実験はビュッフォン(Buffon) の針の実験と呼ばれている。脚注に引用したように彼は肩越 しに棒切れを投げたと伝えられている。でも、いったに何のためにビュッフォンさん1はこのようなことを したのか。針の長さを`、平行線の間隔を L(簡単のために ` < L)として説明しよう。落とした針の一端 図 1: 平行線と針達 は2 本の平行線 D1とD2にあるとして、針が平行線D1と交わる確率P1を計算してみよう。平行線と交 わる確率を知りたければそれを2 倍すればよい。そのため針と平行線とのなす角度を θ、針の指定された端 (たとえば糸通し穴の有る方)とD1との距離をy とする。まず、角度 θ と y は、それぞれ −π ≤ θ ≤ π; 0 ≤ y ≤ L (1.1)1Georges Louis Leclerc Comte de Buffon
Born: 7 Sept 1707 in Montbard, C¯ote d’Or, France Died: 16 April 1788 in Paris, France
At the age of 20 Georges Buffon discovered the binomial theorem. He corresponded with Cramer on mechanics, geometry, probability, number theory and the differential and integral calculus. His first work Sur le jeu de franc-carreau introduced differential and integral calculus into probability theory. He next wrote Th?orie de la terre and became the most important natural historian of his day having great influence across a wide scientific field. He is remembered most in mathematics for a probability experiment which he carried out calculating π by throwing sticks over his shoulder onto a tiled floor and counting the number of times the sticks fell across the lines between the tiles. This experiment caused much discussion among mathematicians which helped towards an understanding of probability.
L
y
l
θ
D
1
D
2
lsin
θ
図2: 平行線と1本の針 の範囲を動く。さらに、 針がD1と交差する ⇔ y ≤ ` sin θ (1.2) である。従って投げられた針のθ と y が上の矩形の範囲 (1.1) に一様な確率で落ちると仮定すると、それが D1と交わる確率はこの矩形と、矩形の中で(1.2) を満たす (θ, y) の作る領域の面積比 Z π 0 ` sin θdθ Z π −π Ldθ となる。ここで分子の積分範囲が[0, π] であることに注意。図 3 参照。sin の積分が − cos であることを思 い出せば、分子分母はそれぞれ Z π 0 ` sin θdθ = ` Z π 0 sin θdθ = `[− cos θ]π0 = −`[cos θ]π0 = −`((−1) − (1)) = 2` Z π −π Ldθ = L Z π −π 1dθ = 2πL となる。したがって、 P1= ` πL (1.3) さらに、針が平行線と交わる確率P は P = 2P1= 2` πL (1.4)L
lsinθ
π
−π
0
図 3: 2つの領域 となる。(1.4) より、針を N 回投げて n 回平行線上に落ちたときは、n/N はこの確率 P を近似しているは ずであるから n N ≈ 2` πL となる。ここで≈ は近似を意味する。だから、N と n から円周率 π を次式のように推定することができる。 π ≈ 2` L N n (1.5) ビュッフォンは、このようにしてπ の値を実験により求める方法(今日の言葉ではモンテカルロ法) を示唆 した。下の表はいにしえの忍耐強い人々の実験結果を示している。([1], [2]) 表 1: ビュッフォンの針の実験による π の推定値 忍耐強い人 やった年 ` N n 推定値2`N/Ln ウルフ 1850 0.8 5000 2532 3.1596 スミス・ダベルディーン 1855 0.6 3204 1218.5 3.1553 ドゥ・モルガン 1860 1 600 382.5 3.137 フォックス大尉 1864 0.75 1030 489 3.1595 ラッツァリーニ 1901 0.83 3408 1808 3.1415929 レイナ 1925 0.5419 2520 859 3.1795 注:平行線の間隔L = 1.0、交わっているか曖昧な場合に 0.5 とカウント ちょっとラッツァリーニの結果は良すぎるような気がするので、思考実験をしてみよう。今L = 10cm、 ` = 7.85398cm として、2回針を投げて1回だけ交わったら、π の推定値として 2` L N n = 2 × 0.785398 × 2 = 3.141592 が得られることになる。そんな安易でいいのかなあ∼。2
もっと簡単なやり方
針を投げないでもビュッフォンさんと同じようなことができる。今、n を適当な自然数(つまり、1, 2, 3, . . . ) とし、x 座標も y 座標も −n と n の間にある整数点(x 座標も y 座標も整数の点)を考える。−n と n の間に挟ま れる矩形領域の一辺の長さは2n だから、植木算によってこのような点は全部で (2n+1)×(2n+1) = (2n+1)2 個ある。さて、そのような点(p, q) を1つ取り出したときそれが、原点 (0, 0) を中心とした半径 n の円の内 部に入るかどうかは p2+ q2< n2 (2.1) が成り立つかどうかを調べればよい。しかも、このような点の総数と(2n + 1)2の比は、おおよそ矩形領 n n -n -n 図 4: 域の面積(2n)2と、原点(0, 0) を中心とした半径 n の円の面積 πn2 の比に近いはずである。つまり、上式 を満たす整数点の総数をsnと書くと sn (2n + 1)2 ≈ πn2 (2n)2 = π 4 であるから、π の近似として π ≈ 4sn (2n + 1)2 が得られる。直感的にはn を大きくして矩形領域を拡大すればこの近似は良くなると考えられる。これで、 痛い思いをしながら針を投げなくても、(2n + 1)2個の点一つ一つについて(2.1) を計算すればよいことに なった。 しかし、何かを投げたいひとにはそのようなやり方もある。今度は、針ではなく小さな小さなビーズを投 げることにしよう。紙の上に正方形とその内接円を描く。そこにビーズを投げて、正方形に入った総数と円 に入った総数の比を計算する。明らかにその比の4倍はπ の近似となる。でも、正方形が小さいと、たく さんのビーズがその外に飛び出してしまってくたびれ儲けとなる。正方形が大きすぎると、その上に均等に ビーズを投げるのが難しい。実際にビーズを投げてπ を求めるのは余り賢くなさそう。3
えーっ?これ、みんな
π
なの?
以上述べたビュッフォンの方法はπ を求める方法としては最悪かも。π を求めるには三角関数の無限級数 展開に基づいたものなど多くの公式が知られており、モンテカルロ法によってπ の多くの桁を計算しよう という酔狂で忍耐強い御仁は今や見あたらない。下にその公式のいくつかとπ を記憶するための符丁を挙 げておく。美しさを味わってほしい。インドの天才ラマヌジャンなんかはも∼ぉ最高。ただし、arctan を 用いた公式はこれ以外にもたくさんたくさんある。 π = lim n→∞ 4 n2 ³p n2− 12+pn2− 22+ · · · +pn2− n2´ π = 4 µ 1 − 1 3+ 1 5 − 1 7 + . . . ¶ ライプニッツ π = lim n→∞ 24n× (n!)4 n((2n)!)2 ウォリス π = 3 + 1 7 + 1 15 + 1 1 + 1 292 + 1 1 + · · · ブラウンカー π = 8 µ 1 1 × 3+ 1 5 × 7+ 1 9 × 11+ · · · ¶ ライプニッツ π = 4 ∞ X n=0 µ 4(−1)n (2n + 1) × 52n+1 − (−1)n (2n + 1) × 2392n+1 ¶ マチン π =√6 × r 1 + 1 4+ 1 9 + 1 16 + · · · オイラー π = 2 µ 1 + 1 3+ 1 × 2 3 × 5+ 1 × 2 × 3 3 × 5 × 7+ 1 × 2 × 3 × 4 3 × 5 × 7 × 9+ · · · ¶ オイラー π = 3 + 1 10 µ 1 + 1 10 µ 4 + 1 10 µ 1 + 1 10 µ 5 + · · · ¶¶¶¶ 一体誰なの? π = 2 + 1 3 µ 2 + 2 5 µ 2 +3 7 µ 2 + 4 9 µ 2 + · · · ¶¶¶¶ オイラー π = 9801√ 8 Ã∞ X n=0 (4n)!(1103 + 26390n) (n!)43964n !−1 ラマヌジャン π = à 12 ∞ X n=0 (−1)n(6n)!(13591409 + 545140134n) (3n!)(n!)36403203n+3/2 !−1 チュドゥノフスキー兄弟 π = 16 arctan1 5 − 4 arctan 1 239 マチン π = ∞ X n=0 1 16n µ 4 8n + 1− 2 8n + 4− 1 8n + 5− 1 8n + 6 ¶ ベイリー、ボールウェイン、プラウフ π ≈ Yes, I have a number.π ≈ May I have a large container of coffee?
π ≈ Wie? O! Dies π macht ernstlich so vielen M¨uh!
4
計算の原理
たとえばライプニッツの公式を使ってπ を 1000 桁まで計算したければ、 4 = +4.000000 . . . 000000 −4/3 = −1.333333 . . . 333333 4/5 = +0.800000 . . . 000000 −4/7 = −0.571428 . . . 571428 とすべての項を(桁上がりを考えて)1000 桁より少し多く書くことから始めなければならない。だから、単 に公式をそのままプログラムすればすむというものではなく、そこがプログラマの腕の見せ所。下に2400 桁を計算してくれるおそらく最も短いであろうC のプログラムを挙げておく。改行くらい入れてよという 声が聞こえそうだが。 int a=10000,b,c=8400,d,e,f[8401],g;main(){for(;b-c;) f[b++]=a/5;for(;d=0,g=c*2;c-=14,printf("%.4d",e+d/a), e=d%a)for(b=c;d+=f[b]*a,f[b]=d%--g,d/=g--,--b;d*=b);}5
π
計算の変遷
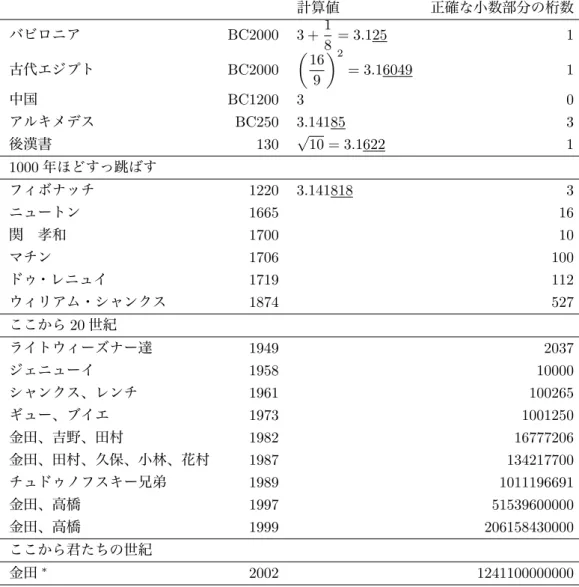
これまで計算されたπ を次の表に振り返ってみよう。日本の小学校で教える π が3になるということは2、 紀元前1200 年の中国の時代に戻るということ?そんなんでいいのかなあ。 世界記録保持者の金田(かなだ) 康正東大教授達がまたしても記録を更新した。2002 年 12 月 06 日付の日 経新聞3 は次のように報じている。 円周率1兆2000 億けた計算、東大が世界新記録「3. 14…」と数が無限に続く円周率を、小 数点以下1 兆 2411 億けたまで計算し、円周率計算の世界新記録を作ったと、金田康正東大教授 らが6 日、発表した。従来の記録は、やはり金田教授らが 1999 年 9 月に作った 2061 億けた。今 回は、新しい計算方法を使い、けた数を一気に約6倍に伸ばした。小数点以下1 兆けた目の数 字は2、1 兆 2411 億けた目の数字は 5 だった。金田教授は、東大情報基盤センターの並列スー パーコンピューター「日立SR8000/MPP」を使い、日立製作所の社員らと今年9 月か ら計算に着手。主計算と検証計算などを合わせ、約600 時間かけて新記録を作った。途中、計 算を止めたこともあり、すべての計算が終わったのは11 月 24 日だった。6
忍耐強く実験してみよう(2時間目)
用具:方眼紙、針、電卓 手順1 約 500 本 (これを N で表す) の針を用意する。針の長さ ` を測定する。平行線の間隔 L(ただし L > `)を何種類か設定する(8の課題1を考慮せよ)。以降の手順は各 L それぞれに対して行なう。 手順2 方眼紙に間隔 L の平行線を引く。 手順3 用意した N 本の針を適当な高さから方眼紙の上に落とす。 2計算が大変なときは3 を使っても良いというのが指導要領だとのこと 3http://satellite.nikkei.co.jp/news/main/表2: π 計算の変遷 計算値 正確な小数部分の桁数 バビロニア BC2000 3 + 1 8 = 3.125 1 古代エジプト BC2000 µ 16 9 ¶2 = 3.16049 1 中国 BC1200 3 0 アルキメデス BC250 3.14185 3 後漢書 130 √10 = 3.1622 1 1000 年ほどすっ跳ばす フィボナッチ 1220 3.141818 3 ニュートン 1665 16 関 孝和 1700 10 マチン 1706 100 ドゥ・レニュイ 1719 112 ウィリアム・シャンクス 1874 527 ここから20 世紀 ライトウィーズナー達 1949 2037 ジェニューイ 1958 10000 シャンクス、レンチ 1961 100265 ギュー、ブイエ 1973 1001250 金田、吉野、田村 1982 16777206 金田、田村、久保、小林、花村 1987 134217700 チュドゥノフスキー兄弟 1989 1011196691 金田、高橋 1997 51539600000 金田、高橋 1999 206158430000 ここから君たちの世紀 金田∗ 2002 1241100000000 手順4 平行線と交差している針の本数 n を数える。 手順5 π の推定値 ˆπ を求める。 手順6 手順 3 から手順 5 を 10 回繰り返す。その結果、π の 10 個推定値 ˆπ1, ˆπ2, · · · , ˆπ10が得られる。 手順7 ˆπ1, ˆπ2, · · · , ˆπ10の平均、標準偏差、95%区間推定を求める。
7
平均・標準偏差・区間推定(3時間目)
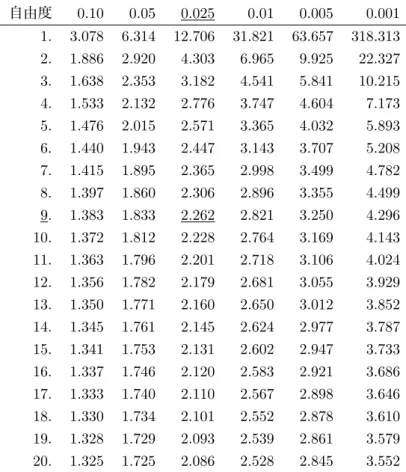
m 個のサンプルデータ x1, x2, · · · , xmが得られたとする。(本実験では、例えば、ˆπ1, ˆπ2, · · · , ˆπ10がサン プルデータとなる。) 1. 平均 ¯x ¯ x = 1 m(x1+ x2+ · · · + xm)2. 偏差平方和 m X i=1 (xi− ¯x)2= m X i=1 x2 i − (Pmi=1xi)2 m = m X i=1 x2 i − m¯x2 3. 標本(不偏)分散 s2 s2= Pm i=1(xi− ¯x)2 m − 1 4. 標準偏差 s s =√s2 5. 母平均 µ の 95%区間推定 上記のx と s と m から母平均 µ が 95% の確からしさで存在する区間を作ることができる。最後のメ¯ モに示したように、t 分布の上側確率 2.5% 点 t(m − 1, 0.025) を用いると P " ¯ x − t(m − 1, 0.025)√s m < µ < ¯x + t(m − 1, 0.025) s √ m # = 0.95 (7.1) が分かる。ここでP [ ] は [ ] 内の起こる確率を示す。つまり、未知の母平均 µ が ¯x−t(m−1, 0.025)s/√m とx + t(m − 1, 0.025)s/¯ √m との間にある確率は 0.95 であることになる。従って、t(9, 0.025) = 2.262 であるから本実験から得られる円周率π の 95% 区間推定は m = 10 の場合 · ¯ x − 2.262 ×√s 10, ¯x + 2.262 × s √ 10 ¸ (7.2) となる。 -4 -2 2 4 0.1 0.2 0.3
0.025
0.025
図5: 自由度 9 の t-分布と 2.5%点8
課題
1. 平行線の間隔 L を適当に3つ以上取り上げて、L の違いによる π の推定精度への影響について考察し なさい。2. 上記の実験で設定した針の長さ l、平行線の間隔 L について、試行回数を N = 100, 500, 1000 と変化 させた場合に、π が π の値に最も近くなる交差回数 nˆ ∗を求めよ。また、n = n∗± 1 となった場合の π の推定値をそれぞれの場合について求めよ。これらの結果に基づき、ビュッフォンの針の実験によ るπ の値の推定精度について考察しなさい。 3. その他、気がついた点について述べなさい。 ¶ ³ hh メモ ii 正規分布と Student の t 分布 平均µ、分散 σ2の正規分布(これを N (µ, σ2) を書く) とはその確率密度関数f (x) が f (x) =√1 2πσexp µ −(x − µ) 2 2σ2 ¶ で与えられる分布であるa。また、自然数n に対して確率密度関数 gn(x) = √1 nπ Γ((n + 1)/2) Γ(n/2) 1 (1 + x2/n)(n+1)/2 を持つ分布を自由度n の t 分布bという。ここで、Γ(·) は Γ(x) = Z ∞ 0 tx−1exp(−t)dt で定義されるガンマ関数である。両者の間に以下の関係が知られている。 「X1, . . . , Xmが互いに独立に正規分布N (µ, σ2) に従うとき、その平均と分散を ¯ X = Pm i=1Xi m , S = s Pm i=1(Xi− ¯X)2 m − 1 とすると √ m( ¯X − µ) S は自由度m − 1 の t 分布に従う。」
aこの分布は偶然誤差の分布法則として数学者Johann Carl Friedrich Gauss (April 30, 1777 - February 23, 1855) によっ
て提案された。ユーロ導入前のドイツの10 マルク紙幣には、彼の肖像の横に正規分布の関数形とグラフが印刷されていた。そ れを手にして喜んでいた私に向かって友人は「10 マルクもらってこんなに喜んだ人を見たことがない」とあきれていた。
bこの分布はGuinness で働いていた統計技師 William S. Gosset によって 1908 年に発見された。会社との契約で本名で発
表できなかった彼はペンネームとしてStudent を選んだため、“Student’s t distribution” とも呼ばれる。しかしなぜ “t” が えらばれたのかはよくわからない。
¶ ³ hh メモ ii 平均の区間推定 自由度m − 1 の t 分布 gm−1(x) に対して Z t −∞ gm−1(x)dx = 0.975 あるいは同じことだが Z +∞ t gm−1(x)dx = 0.025 なる値t (この値を通常 t(m − 1, 0.025) と書き、上側確率 2.5% 点と呼ぶ) を決めると、t 分布が y 軸に 対して左右対称であるaことから Z t(m−1,0.025) −t(m−1,0.025) gm−1(x)dx = 1 − (0.025 + 0.025) = 0.95 となるので、 −t(m − 1, 0.025) < √ m( ¯X − µ) S < t(m − 1, 0.025) となる確率が0.95 であることになる。この条件は簡単な式変形により ¯ X − t(m − 1, 0.025)√S m < µ < ¯X + t(m − 1, 0.025) S √ m と同値である。つまり、95%の確からしさで、未知の平均 µ は ¯X − t(m − 1, 0.025)S/√m と ¯X + t(m − 1, 0.025)S/√m の間にあることが言える。t(m − 1, 0.025) の値は統計学の本に載っているので、実際 に上式の2 つの値を計算することができる。ほんの一部を次のページに載せておいた。このように未 知のパラメータを区間で推定することを区間推定といい、統計学の基本的な考え方の一つである。 a偶関数であるという µ ´
参考文献
[1] N.T. Gridgeman, Geometric Probability and the number π. Scripta Mathematica, 25 (1960), 3, 183– 195.
[2] ジャンポール・ドゥラエ(畑政義訳)「π–魅惑の数」朝倉書店、2001 年 [3] ビュッフォンの針を投げてくれる Java Applet がある:
表 3: t 分布パーセント点 自由度 0.10 0.05 0.025 0.01 0.005 0.001 1. 3.078 6.314 12.706 31.821 63.657 318.313 2. 1.886 2.920 4.303 6.965 9.925 22.327 3. 1.638 2.353 3.182 4.541 5.841 10.215 4. 1.533 2.132 2.776 3.747 4.604 7.173 5. 1.476 2.015 2.571 3.365 4.032 5.893 6. 1.440 1.943 2.447 3.143 3.707 5.208 7. 1.415 1.895 2.365 2.998 3.499 4.782 8. 1.397 1.860 2.306 2.896 3.355 4.499 9. 1.383 1.833 2.262 2.821 3.250 4.296 10. 1.372 1.812 2.228 2.764 3.169 4.143 11. 1.363 1.796 2.201 2.718 3.106 4.024 12. 1.356 1.782 2.179 2.681 3.055 3.929 13. 1.350 1.771 2.160 2.650 3.012 3.852 14. 1.345 1.761 2.145 2.624 2.977 3.787 15. 1.341 1.753 2.131 2.602 2.947 3.733 16. 1.337 1.746 2.120 2.583 2.921 3.686 17. 1.333 1.740 2.110 2.567 2.898 3.646 18. 1.330 1.734 2.101 2.552 2.878 3.610 19. 1.328 1.729 2.093 2.539 2.861 3.579 20. 1.325 1.725 2.086 2.528 2.845 3.552