Vol.34, No.10, 1329/1337 (1998)
3点 検 出に よる近 方場定 常不規則音源 の
3次 元位 置推定†
佐 々 木 公 男 * ・ 平 田 克 己 **
3D-Localization of A Stationary Random Acoustic Source in Near-Field
by Using 3 Point-Detectors
Kimio SASAKI* and Katsumi HIRATA**
For the purpose of developing refined
devices for environmental recognition
in robotics,
a practical
method
for 3D-localization
of a stationary
random acoustical
source in near-field
is proposed by newly introducing 3
fixed-detectors.
By using two pairs
of estimated auto-and cross-spectra
of signals
detected simultaneously
at 3
fixed
detectors,
two sets
of information about difference
in propagation distances
and the amplitude attenuation
of wave propagation are derived in such a manner that the derivation
is
independent of the shape of power
spec-tra of detected random signals
so as to be applicable
to any stationary
random acoustical
source and additive
corrupting
noises
at detectors
are cancelled
out as completely as possible.
Then, by combining these information
with the geometric relation
of signal
detection,
the source position
in 3D-space is estimated. After the principle
of the proposed 3D-localization
and the required conditions
being made clear,
3D-distribution
area of the
posi-tion estimate is
theoretically
evaluated as concentration
ellipsoid,
based on the sampling variations
of estimated
spectra,
and a simple method of evaluating
the 3D-distribution
or localizable
area with prescribed
relative
errors
is derived from the maximum length of major axes of the ellipsoid.
To show the effectiveness
of the theoretical
results
and make clear
the influence
of the source range, SNR, at detection
and spatial
distance
between detectors
on the final
source distribution
or localizable
area, numerical analyses are carried
out by changing them
para-metrically,
the result
of which illustrate
the effectiveness
as well as fundamental characteristics
of the proposed
method under practical
circumstances.
Key Words: 3 point-detection,
3D-localization,
stationary
random acoustic
source, spherical
wave, expected
source distribution
area
1.
は じ め に
我 々人 間の聴覚 は,パ ーテ ィー会場 や機 械工 場 な どの よう
な騒 音 中で も対象 音源 の位 置 や音 を聴 き とる能 力 を もってい
る.こ の聴 覚系 の優 れ た聴 取 能力 を ロボ ッ トに持 たせ る こ と
が で きれ ば,有 用 な ロボ ッ トの環境 認識 シス テムが構 築で き
る もの と考 え られる.
この ような音 源 の3次 元 定位 に資 す る研 究 には,岡 田等 に
よる3マ イクロフ ォン系 に よる3次 元音 源定位 と音声分 離1),
安 藤等 に よる時 空 間勾 配 法 に基づ く3次 元音 源定位 セ ンサ シ
ス テ ム2),な どが あ る.こ れ らは主 と して発 話者 の定位 に応
用 されて いる こ ともあって,い ず れ も確 定的信号 を対 象 と し,
応 用上 不 可欠 な観測 雑音 の影 響 が考慮 され てい ない.そ の た
め,騒 音 中で の不規 則音 源定 位へ の適 用 は きわ めて困難 な も
の で ある.
著 者 等 は,検 出器 の付 加 的回転 を伴 う両耳聴 取法 に よる近
方場 定 常 不規 則 音源 の3次 元 位 置推 定 法 を提 案 したが3),4),
ロボ ッ ト系 へ 応 用 す る場 合 に は,マ イク ロ フ ォン を固定 し,
各点 で 同時 に信号 を受信 ・解析 す る方 が 簡便 であ る.
一 般 に
,近 方場 にお い て2点 検 出法 で取得 可 能 な情 報 は,
音 源 ・マ イク ロフ ォン間の2距 離 であ る5).そ れ ゆえ,平 面
上 の 定位 はで きるが,3次
元の 定位 はで きない.
そ こで本論 文で は,検 出器 を1個 加 え,計3個
の マ イ クロ
フ ォ ンを固定 して用 い る,3点 検 出法 を導 入 した近方 場定 常
不 規則 音 源の3次 元位 置推 定法 を提 案 し,そ の原 理 と種 々の
条 件 下で の位置 推 定精度 の 理論 数値解 析 の結 果 を報告 す る.
以 下,提 案 手法 の前提 条件 明確化 の後,推 定 原理 の定式 化,
推 定値 の統 計 的性 質の理 論 的評価 を行 ない,こ れ に基 づ き推
† 第36回 計 測 自動 制 御 学 会 学 術 講 演 会 で 発 表 (1997・7) 筑 波 大 学 構 造 工 学 系 つ く ば 市 天 王 台 1-1-1 筑 波 大 学 大 学 院 工 学 研 究 科 つ くば 市 天 王 台 1-1-1 Institute of Engeering Mechanics, University of Tsukuba, TsukubaDoctoral Program of Engineering, University of Tsukuba, Tsukuba
(Received September 22, 1997) (Revised April 23, 1998)
1330
T. SICE Vol.34 No.10 October
1998
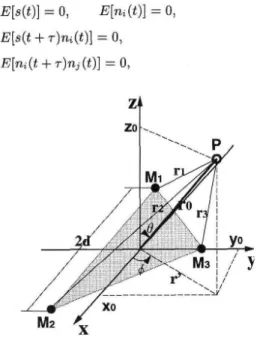
定 値 の 分 布 領 域 を数 値 的 に評 価 す る こ と に よ っ て,本 手 法 の 有 効 性 を 理 論 的 に 明 ら か にす る. 2. 3次 元 位 置 推 定 原 理 2.1 幾 何 学 的 配 置 と前 提 条 件 本 手 法 は,い わ ば3点 測 距 法 に よ り音 源 の 位 置 推 定 を 行 う も の で あ り,以 下 対 象 音 源 は 単 一 とす る.Fig.1に 点 音 源 Pと 検 出 器 の 幾 何 学 的 配 置 を示 す.直 立 水 平 面 にX-Y座 標 を と り,音 源Pか ら放 射 さ れ るGauss性 定 常 不 規 則 信 号 を X-Y平 面 上 で 原 点 を重 心 とす る,一 辺2dの 正 三 角 形 の 頂 点 M1,M2,M3に 配 置 した3検 出 器 で 受 信 す る.そ の3つ の 受 信 信 号 か ら,y軸 上M3点 で 検 出 した 信 号 を 共 有 す る,2 組 の2信 号 を 自 己 お よ び 相 互 ス ペ ク トル 解 析 し た 結 果 か ら, 音 源Pの 極 座 標(r0,φ,θ)を,推 定 す る こ とが 本 研 究 の 目 的 で あ る.こ こ で,次 の 仮 定 を 置 く. (1) 波 動 の 伝 搬 は 球 面 的 で あ る. (2) 信 号 受 信 時 に 加 法 的 ノ イ ズ が 重 畳 し,そ れ ら は相 互 に 無 相 関 な 定 常Gauss的 で 音 源 信 号 と は独 立 で平 均 値0,同 一 パ ワ ス ペ ク トル を持 つ . (3) 音 源 信 号 と ノ イ ズ の パ ワ ス ペ ク トル は い ず れ も十 分 滑 ら か で,そ の 最 狭 ピ ー ク の 半 値 幅 の 逆 数 に 比 べ て 観 測 デ ー タ 長 は 十 分 に長 い. (2)のGauss性 の 仮 定 とパ ワ ス ペ ク トル の 同 一 性 は,必 ず し も本 質 的 で は な い が 実 際 的 状 況 を 反 映 した もの で あ り,(3)は B-T法 に よ る高 精 度 パ ワ ス ペ ク トル 推 定 の 可 能性 を意 味 す る. 上 記 仮 定 の 下 に お い て は,各 検 出 器 に お け る 観 測 信 号 は, 次 式 で 表 せ る.xi(t)=s(t-Di)+ni(t),i=1,2,3.
(1)
こ こ でs(t)は 音 源 信 号,n(t)は 観 測 加 法 ノ イズ で あ り,い ず れ も平 均 値0の 定 常 正 規 信 号 で 互 い に無 相 関,つ ま り E[s(t)]=0, E[ni(t)]=0, E[s(t+T)ni(t)1=0, E[ni(t+T)nj(t)]=0,Fig. 1 Geometry of signal
detection
i,j=1,2,3,i≠j, (2) と す る.こ こ でE[・]は 集 合 平 均 演 算 を 表 す.ま た,riとDi は,そ れ ぞ れ 音 源 と 検 出 器 間 の 距 離 お よ び 伝 搬 遅 れ 時 間 を 表 す.音 速 をc0と し た 場 合,伝 搬 距 離 差rdは, rdi=r3-ri=c0(D3-Di),i=1,2, (3) と 表 さ れ る.式(2),(3)よ り,xi(t)の 自 己 パ ワ ス ペ ク ト ル お よ び 相 互 パ ワ ス ペ ク ト ル は,s(t),n(t)の 自 己 パ ワ ス ペ ク トル Φss,Φnnを 用 い て,そ れ ぞ れ 次 の よ う に 表 さ れ る.
~~.x=(f)=2~55(f)+~~~(f),
(4)
`)~ixj(f)=4~ss(f)exP(-j27rf(Di-Di)),(5)
i,j=1,2,3.
以 上 の こ と を 踏 ま え て,次 に伝 搬 距 離 差 と振 幅 減 衰 情 報 の 抽 出 法 と3次 元 位 置 推 定 法 に つ い て 述 べ る. 2.2 3次 元 位 置 推 定 原 理 上 述 の よ う に,音 源 信 号 と加 法 ノ イ ズ が い ず れ も平 均 値0 のGauss性 定 常 信 号 で あ り互 い に 無 相 関 で あ る の で,相 互 パ ワ ス ベ ク トル が ノ イズ の 影 響 を 受 け ず に精 度 良 く推 定 で き る.そ こ で,伝 搬 距 離 差rdは,相 互 パ ワ ス ペ ク トル の位 相 の,周 波 数 に対 す る傾 き を 用 い て 次 式 の よ う に推 定 で きる.U)](6)
Tdi~J)=T3-?'i=otan-1Im2
~rfRe4)xx3(f)]
仮 定(3)か らφx3xi(f)の 位 相 は,周 波 数fに 関 し て 滑 ら か に 変 化 す る が,実 際 にtan-1{・}の 計 算 を行 う と,2π モ ー ドの 値 しか 求 ま ら な い.そ こで,必 要 に応 じて 位 相 の ア ン ラ ップ に よ り こ れ を周 波 数fの 周 りで 局 所 的 に連 結 し,そ の 傾 き か ら伝 搬 距 離 差 γdiを推 定 す る. 振 幅 減 衰 情 報Bは,各 受 信 信 号 の 自 己 パ ワ ス ペ ク トル の 差 を 相 互 パ ワ ス ペ ク トル の 絶 対 値 で 規 格 化 した,T3-r2(7)
~~3yiT3Pi に よ っ て 抽 出 で き る.こ の 量 は 自 己 パ ワ ス ペ ク トル の 差 を取 り,加 法 ノ イ ズ の パ ワ ス ペ ク トル を相 殺 し,相 互 パ ワ ス ペ ク トル の 絶 対 値 で 規 格 化 し て い る の で,結 果 的 に 伝 搬 距 離r3 とriに の み 依 存 した も の に な る.そ れ ゆ え 式(6),(7)を 連 立 し て 解 け ば,2組 の 距 離r3,ri(i=1,2)が 求 ま る.そ こで 2組 のr3の 算 術 平 均 を 用 い る こ と に よ り,r3に 関 して は さ ら に 高 精 度 の 情 報 抽 出 が 期 待 で き る. ま た,Fig.1に 示 し た幾 何 学 的 関係 か ら次 式 が 成 立 す る.ri+r22=2ro2+rodsinsin+d2,(8)
rl2-r22=4rodsincos,(9)
rig+r22+r32=3ro2+4d2.(10)
式(6),(7)を 連 立 し て 求 め たr1,r2,r3を 式(8)∼(10)に 代 入しr0,φ,θ に つ い て 解 け ば,求 め る 推 定 値r0,φ,θ は, 22^21r dlIlrd2I2
o=1+-r3-4d211)
r3BB22
-1JlJ2~
=tan^^^^
rd2B1J1-rd1B2J2
xro+d2-r3,(12)
8=sin-1i13(2+-d2-r3.
4rod3rd2B1J2-+'rdB2Jl^^(13)B
1B2
と な る.但 し,Ii=B2+4+2/B2+4,
Ji=Bit+4+2,i=1,2.
(14)
以 上 が,単 一 周 波 数fに 近 い 波 動 を 利 用 し た3点 検 出 法 に よ る3次 元 位 置 推 定 の 基 本 原 理 で あ り,相 互 パ ワ ス ペ ク ト ル を 関 連2信 号 の 自 己 パ ワ ス ペ ク トル の 積 の ル ー トで 正 規 化 し た コ ヒ ー レ ン ス 関 数 の 絶 対 値 が1に 近 い,信 号 対 雑 音 比 (SNR)の 良 い 周 波 数 の 選 定 に よ り良 好 な 推 定 が 期 待 で き る. そ こ で,式(6),(7)の 代 わ り に,仮 定(3)よ り受 信 信 号 の ス ペ ク ト ル 間 の 線 形 従 属 性 の 強 い,中 心 周 波 数f0の 帯 域 BH=[fl,fh]に わ た っ て こ れ ら を 積 分 した,rdi(fo)=1rdz(f)df,(15)
Bi(fo)=B2(f)df,(16)
を用 い れ ば よ り高 精 度 な 推 定 が 期 待 で き る. 2.3 ス ペ ク トル 推 定 値 の 統 計 的 性 質 B-T (Blackman-Tukey)法 で 推 定 さ れ る 自 己 お よび 相 互 パ ワ ス ペ ク トル の1次,2次 の 統 計 的 性 質 に 関 し て,観 測 時 間 Tがxi(n),xj(n)の 相 関 時 間 に 比 べ て 十 分 に長 い 場 合 に は, 以 下 の よ う な性 質 が 知 られ て い る6).E[`~xixj(f)]=(f)+0(1/T
),.
(17)
Var[Re[~xix;(1)]]
=C[~xixi(f)~xjxj(f)+Re2[I(1)]
-Im2[4(f)]l2+0(1/T)
,
(18)
Var[Im[4xix;(f)]]
=C[4xixi(f)I(f)+Im2[4xixj(f)]
-Re2[4(f
)]/2+0(1/T),
(19)
Cov[Re[I(f)]~Im[~xixj(f)]
=C.Re[I(f)]Im[4(f)]+0(1/T),
(20)
Cov[3(f)~'xjxj(f)]
=CI4xixj(f)I2+0(1/T),
(21)
COV[~xixi(1)1Re[I(1)]]
=C(f)Re[Y(f)]+0(1/T),
(22)
Cov[&zxi(f),Im[~xixj(1)]]
=C~xixi(f)Im[4xixj(1)]+0(1/T),
(23)
但 し,E[・]は 期 待 値,Var[・]は 分 散,Coυ[・]は 共 分 散 を 示 す.
Re[・],Im[・]は,そ れ ぞ れ 複 素 数 の 実 部,虚 部 を表 し,Cは 平 滑 化 ラ グ 窓 の エ ネ ル ギ ー と観 測 デ ー タ長 の 比 で, 1/2ztM
IW(f)12dfof~w2(m)
C,_-1/2~t_m=-M
(24)TT
と表 さ れ,B-T法 に お け る推 定 値 の 変 動 を評 価 す る 際 の 基 本 的 な パ ラ メ ー タで あ る. 3. 推 定 精 度 の 理 論 的 解 析 3.1 推 定 精 度 の 理 論 的 定 式 化 こ こ で は,ま ず 伝 搬 距 離 差rd,お よび 振 幅 減 衰 情 報Bの 推 定 誤 差 を求 め,そ の 結 果 を 用 い て 距 離,方 位 の推 定 値r0,φ,θ の推 定 誤 差 を 導 く.そ の 際,2.1で 述 べ た 仮 定(2),(3)か らパ ワ ス ペ ク トル 推 定 値 の バ イ ア ス は 無 視 で き る. 伝 搬 距 離 差 の 推 定 値rdは,式(6)で 表 さ れ,こ れ を 真 値 rdの ま わ りで テ ー ラ ー 展 開 し線 形 近 似 す る と,CORe[43i]8Im[43i]-Im[~3i]bRe[~3i]
rd2:I~
3iI2
(25)
と な る.こ こ で δA=A-Aと 定 義 す る.式(25)の 集 合 平 均 を と れ ば,(2),(3)の 条 件 か ら相 互 パ ワ ス ペ ク トル 推 定 値 φ3iの バ イ ア ス は 無 視 で き,し た が っ て そ の 実 部,虚 部 の バ イ ア ス も無 視 で き る の で,そ れ らの 真 値 か らの 偏 差 δIm[Φ3i], δRe[Φ3i]の 集 合 平 均 は 無 視 で き,そ の 結 果,rdiの バ イ ア ス は無 視 で き る こ と に な る.つ ま り, E[δrdi]=0. (26) ま た,式(25)を2乗 した も の の 集 合 平 均 に,2.3で 記 し た 自 己 及 び 相 互 パ ワ ス ペ ク トル の 平 滑 化 ス ペ ク トル の 統 計 的 性 質 を 用 い れ ば, 22VarrCCO4ii~33-I~3ilX27)dil.2
~f2II3iI2
を 得 る.こ こ で,Cは 平 滑 化 窓 の エ ネ ル ギ ー と デ ー タ 長 の 比 で 決 ま る 定 数 で あ る. ま た,振 幅 減 衰 情 報 の 分 散Var[Bi(f)],さ ら に 共 分 散 Coυ[rdi,rdj], Coυ[Bi,Bj], Coυ[Bi,rdi], Coυ[rdi,Bj]に つ い て も 同 様 な 操 作 を 行 な う こ と に よ り,次 の 式 を 得 る.^(~+133-2I~3iI23(-33)2
I~3iI223iI2
+(4ii-433)2ii433(28)2I
3iI4
cOC
COv[rdi,rd3]=2
7tf2~3iI2I~3jI2.
1332 T. SICE Vol.34 No.10 October 1998
{Re[3i]Re[43j](433Re[Iij]-Re[43j~3i])
-Re[3i]II11[3j](33Im[~ji]+Im['3jI3i])
-Im[3i]Re[3j](33Im[ij]+Im[I3jI3i])
+Im[~3i]Im[43j](I33Re[Iij]+Re[43j13i])},
(29)
Cov[Bj,Bj]
=Ci1()ij
I3i3jI2-I~3iI2-I~3jI2+332)
{Re[3j]Re[ij~3iJ1
3i11~3j
-33I~3jI2}
ii-X33{Re[~
3i]Re[~ji~3j]1
3j11~3iI3
+Im[~3i]Im[4jiI3j]-~33I~3iI2}
+-33)jj-41'33)2I'I
3iI3I'3iI3
ReRe+Re[3j3i])
+Re[3iJIm[3j](33Im[ij]+Im[I3i43j])
+Im[3i]Re[3j](I33Im[ji]+Im[13j43i])
+Im[I3i]Im[j](Re[4ij]-Re[3jI3i])
(30)
(31)COV[Bifrdi]=0,
^~0Cov[rd~,Bj]-c2
~rf
x(Re[~3i]Im[~ji~3j]I~
3i121~3j
-Im[~gi]Re[~ji~3j])
-~JJ-X33{~33Im[~ij]ReL~3i~3j]
~33Re[~ij](Re[~3i]II11[~3j]
-Im[ 13i]Re[43j])
+Im[~3j~3i]Re[~3i~3j]
-Re[~3j~3i]Im[~3i~3j]}
(32)
以 上 の よ う に 導 出 した 式(27)∼(32)の 分 散 ・共 分 散 に式 (4),(5)の 自 己 お よび 相 互 パ ワ ス ペ ク トル,な ら び に 幾 何 学 的 関 係 式(8)∼(10)を 代 入 す れ ば,以 下 の 評 価 式 を得 る.VarC2(rig+r32)SNR+ri2r32[rd]=C,
(33)
Var[B,.]_(i(rig-f-r32)
2ri2r32SNR2X{(rig+r32)SNR+ri2r32},(34)
Cov[rdi,rdj]=C~0r3
(35)2
rf2SNR
Co=Cri(r32-2)+rj(r-r)
rjr32rir32rirjr31ri(r3-ri)
+
r32rirj+SNRrj+
rj(r3-rj)
+2rirj
+rirjr3+(r3-r)(r32-rj2)SNR2
x2+1
(36)
rirjr32SNRrirjJ
Cov[I'dz,Bj]=0.(37)
但 し,i,j=1,2 こ れ ら の 式 を用 い て 距 離r0,お よ び 方 位 φ,θ の 推 定 値 の 分 散,共 分 散 を評 価 す る.ま ず,式(11)で 得 ら れ た 距 離 の 推 定 値rbを 線 形 近 似 す る と,真 値 か ら の 偏 差 は,br=2r(oEi+arbrd(38)
aBiard2 但 し, aro1rd B23roBi2Bi2+4Bi2+4+2)(ri+2r3(39)
arorl(40)(2
ri+r3)a
rdi3ro2rdi
と な る.よ っ てr0の 分 散 は,次 の よ う に 評 価 さ れ る.Var[r0]=Var[B1]+Var[B2]aB
1aB2
+(Var[rdl]+Var[rd2]
arpar
+2aBaBCov[B1,B2]
aror0
andandCov[rdl,rd2].(41)
方 位 φ,θに つ い て も同 様 に計 算 す れ ば,次 の よ う に な る.Var[]=Var[EiJaB+(Var[2]
Ba2
a~
__Var[d
i}~
+a ndr+and-)Var[rd2]
a~a~bC
ov[Bl,B2]aB
laB2
Cov[rd1,rd2],(42)a
rdlard2
aea8V
ar[]=2a
iVar+2Var[E2}aB2
ae2ae2+
arVar[rdi]+andVar{d2]
dl r aeaeaBicov[B1,BaB2
aet90
+2Cov[rdi,rd2],(43)a
rd1ard2
Cov[ro,cb]=Var[Bi]
aroaq5+
22Var[B2]+aroq5Var[rd1]aBaBand1and1
+aroaVarrd+Cov[Bi,B2]a
ndand[2]aBiaB2
aroa
aB2aBicov[Bi,B2]
aroa+C
ov[rdi,rd2]a
rdlard2
aroa(44)+C
ov[rdi,rd2]a
nd2and1
aroaeC
ov[ro,8]=aB
iaBiVar[Bi]
aroaearoae+
aB2aB2Var[B2]+andandVar[rd1]
aro59aro
rdVar[rd2]+Cov[Bi,B2]ard2ad2aBiaB2
aro59+C
ov[Bi,B2]aB
2aBi
aroae+C
oy[rdi,rd2la
rdlard2
aroae
ard2ardl
Cov[q,8]=a~b59Var[Bi]
aBiaBi
a;aeV
arB2]+a~ae+Var[rd1]aB
2aB2[ardlardl
+a98Var[rd2l+aaeCov[Bi,B2]a
rd2ard2aBiaB2
+abaecov[Bi,B2]aB
2aBi
+acae[rd1,rd2la
rdlard2
+aaecov[rd1,rd2](46)a
rd2ard1
但 し,(
3 a93rdiIix{risin+3cos
aBi2rdcos9
-2rsin+23dsin92rir3
36ro,
(47)
rdi2rdirodcos9ri+cos 2ri+r32rsin+2sin9q536
r
(48)
a
-3rdiIZx
aBi2rdsin9
(2ri+r3)cos5
Ti(cosq5-3sin-3,
(49)
ard
cos
ricos3sin
(50)
こ こ で,Bi2+4+2I
i=
(51)
Bi2Bi2+4
3.2 推 定 精 度 の 理 論 的 評 価 式(39)∼(51)がr0,φ,θ の 推 定 誤 差 を理 論 的 に 評 価 す る 上 で の 基 本 式 で あ る.こ れ ら は,い ず れ も式(33)∼(37)で 与 え ら れ るrdi,Bjの 分 散,共 分 散 の 線 形 結 合 で あ り,後 者 の 各 パ ラ メー タ に 関 す る 依 存 性 か ら,全 般 的 にSNRが 良 く周 波 数 が 高 い ほ ど,ま た,平 滑 化 窓 パ ラ メ ー タCが 小 さ い ほ ど高 精 度 の推 定 が 可 能 で あ り,こ れ らが こ の 手 法 に お い て 重 要 な 意 味 を 持 つ パ ラ メ ー タ で あ る こ とが 推 測 で きる. ま た,こ れ らの 式 は,r0が 遠 距 離 に な る に っ れ てri(i= 1,2,3)が 大 き くな る と共 に,そ れ らの 比 が1に 近 くな る の でBiが0に 近 づ く.そ れ 故r0→ ∞ の 極 限 で はrdi,Biの 分 散 ・共 分 散 が 無 限 大 に発 散 す る こ と に起 因 しr0,φ,θ の 分 散 ・共 分 散 も発 散 して し ま う.結 局,遠 方 場 で は振 幅 減 衰 の 情 報 が 失 わ れ て し ま い,距 離 推 定 の 意 味 が 消 失 す る こ と を示 し て い る.遠 方 場 を対 象 とす る場 合 は,信 号 の 伝 搬 時 間 差 の み を 推 定 す れ ば,第1章 で 述 べ た 従 来 の 方 法 と 同 様,方 位 推 定 は 可 能 で あ る.検 出 器 の 間 隔dに つ い て は,分 母 に 多 く現 れ て い る の で,d→0で そ れ ぞ れ の分 散 ・共 分 散 が 無 限 大 に 発 散 す る.そ れ ゆ え,実 際 的 配 置 で は,検 出 器 間 隔 の 制 限 の 範 囲 内 で,極 力 大 き く離 し て 配 置 させ る必 要 が あ る. 以 上 の よ う に音 源 位 置 の 推 定 値 と各 パ ラ メ ー タ と の 関 連 性 の 詳 細 な 検 討 は,式 の 構 造 が 複 雑 な た め,き わ め て 困 難 で あ る.そ こで 次 章 で は,こ こ ま で に 導 出 した 理 論 式 を も と に し て 行 な った,計 算 機 に よる 数 値 解 析 結 果 に つ い て 述 べ る. 4. 数 値 解 析 結 果 こ の 章 で は,ま ず 極 座 標 下 で の 推 定 値(r0,φ,θ)の 分 布 領 域 を,直 交 座 標(x,y,z)の3次 元 領 域 で 表 現 す る.そ の た め, 2.1節 の 仮 定(2)で 述 べ た 推 定 値 の 正 規 性 と,3.1節 の 線 形 評1334 T. SICE Vol.34 No.10 October 1998 価 に着 目 し て,与 え ら れ た 確 率 の も とで 真 値 が 存 在 す る確 率 集 中楕 円 体 に よ る 評 価 をす る. 4.1 解 析 方 法 計 算 の 便 宜 上,位 置 推 定 値r=(r0,φ,θ)Tを 極 座 標 か ら直 交 座 標x=(x,y,z)Tに 変 換 す る.変 換 行 列 をHと す る と, 位 置 推 定 誤 差 は xε=Hrε, (52) と な る.こ こ で,Xε=(x-x0,y-y0,z-z0)T,rε= (r0-r0,φ-φ0,θ-θ0)Tで あ り,Hは 次 式 で 与 え ら れ る.
sin9cosqrocos9cos-rosin9sin~b
H=sin9sin~brocos9sin~b-rosin9cosc
cos9-rosin90
(53)
仮 定 よ り(x,y,z)は,(x0,y0,z0)の 不 偏 推 定 量 で,正 規 分 布 に従 う もの と考 え ら れ る の で,そ の 確 率 密 度 関 数 は, Pε(x,y,z))exp2XeAXe,(54)=(I2I312IAI1/2i
で 与 え ら れ る.但 し,Λ ε は 直 交 座 標 系 にお け る 位 置 推 定 誤 差 ベ ク トルxε の 共 分 散 行 列 で あ り,Var[y]Cov[x,y]Cov[x,z]
Ae=Cov[x,y]Var[y]Cov[y,z],
(55)
Cov[x,z]Cov[y,z]Var[z]
と定 義 さ れ,極 座 標 系 の も とで の 位 置 推 定 誤 差rε の 共 分 散 行 列Rε と は 次 の 関 係 に あ る. Λε=HRεHT (56) こ の と き,式(54)の 指 数 部 の2次 形 式 が 一 定 値Q以 下 に な る 領 域 は 楕 円 体 と な る.そ の 軸 の 向 き は,式(55)で 定 義 し た 共 分 散 行 列 Λεの 固 有 ベ ク トル υκ(κ=1,2,3)と 一 致 し, 固 有 値 をλκと す れ ば 軸 の 長 さ は,λ κQと な る. ま た,(x,y,z)が 楕 円 体 の 内 部 に あ る 確 率Pは,次 式 で 与 え られ る7).1-x2/2d2~-Q/2(57)P
-2
0ex--=e.2~r2~r
推 定 値 の正 規性 と線 形 近 似 が成 立 す る限 り,確 率Pで
推
定 値 が 真値 の まわ りに分 布 す る3次 元 領域 が 式(55)で 定 義
した共分 散行 列 Λεの 固有値 分析 に よ り簡潔 に求 まる.
以 上が3次 元 空間 内で の厳 密 な議論 で あるが,よ り簡単 な
指 標 で推 定値 の分 布領 域 を評価 した い場 合 には,例 えば最 大
固有値 に よって求 まる集 中楕 円体 の長 軸の長 さ,と い うス カ
ラ ー指 標 のみ に着 目す るこ とに よって さらに簡便 にこれ を行
な う ことが可 能で あ る.具 体的 には,得 られた集 中楕 円体 の
長 軸 の1/2を,音
源 まで の距離 で規 格化 した ものが 一定 の相
対 誤差,例 えば30%以
下 となる領域,つ ま り
1AmaxQ~0
.3,
(58)2
rn
な る 領 域 な ど を 採 用 す る.こ れ に つ い て も数 値 解 析 に よ っ て 調 べ て み る. 4.2 解 析 結 果 本 解 析 で は,ま ず,広 い 範 囲 の 集 中 楕 円 体 の お お ま か な 分 布 性 状 を 把 握 す る た め,Table 1(a)の よ う に,SNR,検 出 器 間 隔2dを パ ラ メ ー タ と し て,方 位 φを0∼90゜,ま た,θ を15∼75゜ の 範 囲 に 渡 っ て そ れ ぞ れ15゜ 単 位 で 変 化 さ せ た.Table 1 Parameters in numerical analyses (a) Concentration ellipsoid
Fig.
2 Example of
concentration
ellipsoids
where parameters
are fixed
as SNR: 40dB, r0:1m,
2d:1m
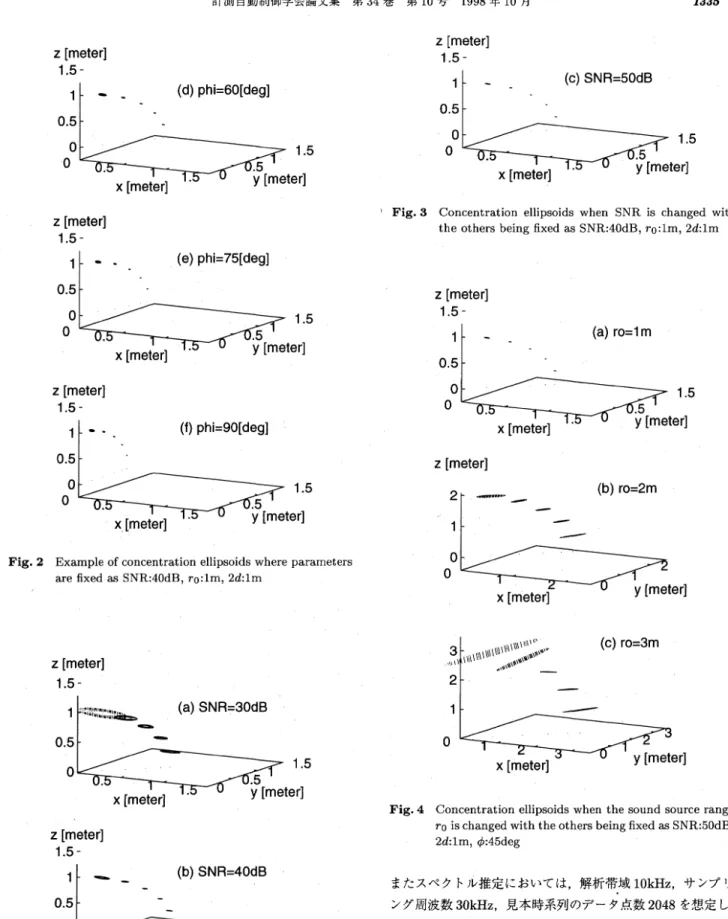
Fig. 2 Example of concentration ellipsoids
where parameters
are fixed as SNR:40dB, r0:1m, 2d:1m
Fig. 3 Concentration ellipsoids when SNR is changed with the others being fixed as r0:1m, 24:1m, φ:45deg (continued)
Fig. 3 Concentration ellipsoids
when SNR is changed with
the others being fixed as SNR:40dB, r0:1m, 2d:1m
Fig. 4 Concentration ellipsoids when the sound source range r0 is changed with the others being fixed as SNR:50dB, 2d:1m, φ:45deg ま た ス ペ ク ト ル 推 定 に お い て は,解 析 帯 域10kHz,サ ン プ リ ン グ 周 波 数30kHz,見 本 時 系 列 の デ ー タ点 数2048を 想 定 し, Bohmanの 窓(C=0.0264)を 使 用 した.こ れ らの 条 件 で,ま ず 単 一 周 波 数1kHzの 音 源 に対 す る 推 定 値 の ば ら つ き を 示 す 確 率 集 中 楕 円 体 を示 し,推 定 誤 差 の 評 価 を行 な う.こ こ で 確 率 パ ラ メ ー タQは4と し,式(57)よ り確 率 は,約74%と な る.次 に,式(58)で 提 案 した 簡 便 な1次 元 の 評 価 指 標 に 基 づ き,指 定 した 最 大 相 対 誤 差 以 下 で 音 源 の 定 位 可 能 領 域 を導 出 す る た め,Table 1(b)に 示 す よ う に θを,1゜ 単 位 で1゜ ∼
1336 T. SICE Vol.34 No.10 October 1998
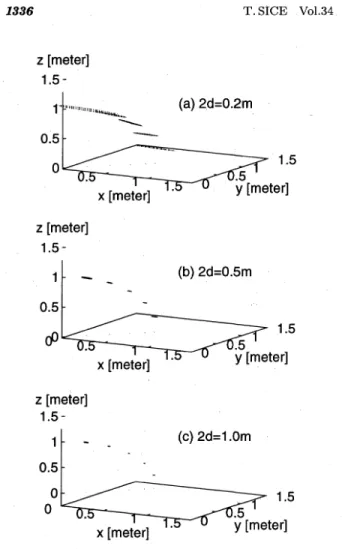
Fig. 5 Concentration ellipsoids when distance 2d between detectors is changed with the others being fixed as SNR:50dB, r0:1m, φ:45deg 90゜ ま で 細 か く変 化 させ て 数 値 的 に 検 討 した. Fig.2は,r0が1.0m,SNRが40dB,2dが1.0mの 場 合 の 確 率 集 中楕 円 体 で 音 源 の 方 位 φ,θに よ っ て 比 較 した も の で あ る.全 体 的 に θ が 小 さ い 時,つ ま り音 源 がz軸 に 近 い と き,推 定 精 度 が 悪 くな っ て い る.こ れ は,本 手 法 で は,全 て の 検 出 器 を,z軸 上 の 点 か ら等 距 離 に あ るX-Y平 面 上 に 配 置 し て お り,θ →0の 時,2組 の 伝 搬 距 離 差rdi(f)と 振 幅 減 衰 の 情 報Bi(f)が い ず れ も0に 近 付 き,式(6),(7)の 独 立 性 が 失 わ れ て し ま う.こ れ ら の独 立 性 を前 提 と して 求 め た 音 源 の 極 座 標 パ ラ メー タ の推 定 式(11)∼(13)は,い ず れ も0に 近 い 値 で の 割 算 を含 む の で,標 本 変 動 の 影 響 を 大 き く受 け 易 く な り,そ の 結 果,推 定 精 度 が 劣 化 す る もの と 考 え ら れ る.こ の こ と は,r0,φ,θ のrdiお よ びBiに 関 す る 偏 微 係 数 の 算 出 式(39),(40),(47)∼(51)と,こ れ ら を用 い た 分 散,共 分 散 の 算 出 式(41)∼(46)か ら も理 論 的 に 予 測 さ れ る こ と で あ る. ま た,φ が30゜ の 時,そ の 精 度 は 明 らか に 期 待 で きる も の で な い の で こ の 図 か ら は 省 い た.こ の 場 合,Fig.1か ら分 か る よ う に,音 源 は検 出 器2,3の2等 分 面 上 に あ る の で,こ れ ら の 間 の 距 離r2とr3が 等 し く,rd2(f),B2(f)が と も に0に な り,上 記 と 同様 の 理 由 に よ り推 定 値 の 分 散,共 分 散 が発 散
Fig. 6 Examples of localizable areas where SNR and the dis-tance 2d between detectors are changed parametrically in (a) and (b), respectively
して し ま う た め で あ る. Fig.3は,検 出 器 の 間 隔 ・音 源 まで の 距 離 を共 に 一 定 に し, SNRが(a)30dB,(b)40dB,(c)50dBの そ れ ぞ れ の 場 合 を 示 した も の で あ る.SNRが 良 い ほ ど楕 円 体 は 極 度 に小 さ く な り,精 度 が 良 くな る の が わ か る.つ ま りSNRは,本 手 法 に お い て 重 要 なパ ラ メ ー タで あ る とい う こ と に な る.Fig.4 は,音 源 まで の 距 離r0の み を(a)1m,(b)2m,(c)3m,と 変 化 させ た もの で,音 源 が 遠 い ほ ど楕 円 体 は,距 離 方 向 に長 く な っ て い る の が わ か る.近 い ほ ど距 離 分 解 能 は,良 くな っ て い る.ま た,Fig.5で は,検 出 器 の 間 隔2dの み を(a)0.2m, (b)0.5m,(c)1m,と 変 え て 比 較 した もの で,前 章 の 理 論 的 解 析 で も 述 べ た よ う に,間 隔 の 広 い ほ うが 推 定 精 度 は 確 実 に 良 くな っ て い る こ とが 知 れ る. 次 に,式(58)で 提 案 した 簡 便 な1次 元 の 評 価 指 標 に 基 づ き,導 出 した 音 源 定 位 可 能 領 域 に つ い て の 検 討 結 果 を 示 す. Fig.6は,SNRと 検 出 器 の 間 隔(2d)を 変 え た 場 合 の 結 果 の 比 較 で あ る.こ こで,横 軸 は 音 源 のX-Y平 面 へ の 射 影 距 離 で あ る.こ の 図 よ り,SNR向 上 に よ り推 定 精 度 が 良 くな っ て い る の が 明 らか で あ る.例 え ばSNRが30dBか ら40dBに な る と,定 位 可 能 領 域 は 約1.5倍 に,50dBに な る と約2∼3 倍 に拡 大 して い る.ま た,検 出 器 の 間 隔 を 広 く と る と,定 位 で き る 領 域 は そ れ に比 例 して,広 が っ て い る. こ こ で,こ れ らの 結 果 の 意 味 を 考 え て み る.式(58)の 指
標 は,言 わ ば,集 中 楕 円 体 に外 接 す る 最 小 の 球 面 の 半 径 とい う,1次 元 の 指 標 で 集 中 楕 円 体 の 広 が り を簡 便 に 評 価 し,最 悪 の 場 合 で も位 置 推 定 値 が 相 対 誤 差30%以 下 に収 ま る こ と を 要 求 す る も の で あ る.Fig.2∼Fig.5の 結 果 を 見 る と,集 中 楕 円 体 の 広 が りが 相 対 的 に大 きい 場 合 に は,い ず れ の 楕 円 も 相 当 偏 平 に な っ て い る.そ れ ゆ え,最 大 相 対 誤 差 を30%に 設 定 し て は い る が,実 際 の相 対 誤 差 は,そ れ よ りず っ と 少 な い もの と考 え ら れ る. 以 上 の 評 価 結 果 よ り,提 案 手 法 で は 高SNRで の ス ペ ク ト ル 情 報 の 抽 出 が,基 本 的 に 重 要 な役 割 を 果 た す こ とが 知 れ た. 2.2節 で もふ れ た よ う に,高SNRな 周 波 数 成 分 の 利 用,あ る い は そ の よ うな 帯 域 で の 平 均 的 な情 報 抽 出,更 に は 高 次 ス ペ ク トル 解 析 の 利 用 な ど に よ っ て,高SNRな 情 報 抽 出 が で き る も の と考 え ら れ る. 5. 結 論 3点 検 出 法 に よ る 近 方 場 音 源 の3次 元 位 置 推 定 に 関 して, 従 来 よ り利 用 さ れ て き た 伝 搬 距 離 差 の 情 報 に 加 え て,振 幅 減 衰 の 情 報 を 利 用 し た3次 元 位 置 の 推 定 法 を提 案 し,そ の 有 効 性 と特 徴 を 明 ら か に す る た め に理 論 ・数 値 解 析 を行 い,次 の よ う な 結 果 を得 た. (1) 観 測 雑 音 の 存 在 す る一 般 的 条 件 下 で 観 測 時 系 列 の 自 己 お よ び相 互 パ ワス ペ ク トル の 情 報 か ら観 測 ノ イ ズ の 影 響 を 相 殺 した 形 で 抽 出 し た伝 搬 距 離 差 と波 動 の 振 幅 減 衰 の 情 報 よ り音 源 の3次 元 位 置 を推 定 す る方 法 を提 案 し た. (2) 利 用 パ ワ ス ペ ク トル の統 計 的 変 動 の 評 価 結 果 に基 づ き, 位 置 推 定 ベ ク トル の バ イ ア ス と共 分 散 行 列 を 評 価 す る と と も に,位 置 推 定 値 が 指 定 した 確 率 の 下 で 分 布 す る領 域 を 確 率 集 中楕 円 体 と して,理 論 的 に 評 価 した. (3) 最 終 的 な 推 定 値 が 検 出SNR,検 出 器 間 隔,音 源 の 距 離 と方 位 の 各 パ ラ メ ー タ に よ って ど の よ う に 変 動 す る か を, 理 論 的 に 考 察 す る と と も に,確 率 集 中楕 円 体 の 視 覚 化 を 通 じて 数 値 解 析 的 に 明 確 化 した. (4) 音 源 の 位 置 推 定 ベ ク トル の 共 分 散 行 列 の 固 有 値 か ら定 ま る 確 率 集 中 楕 円 体 の 長 軸 を指 標 と して,簡 便 に音 源 位 置 推 定 値 の 相 対 誤 差 を評 価 す る 方 法 を考 案 した. (5) 与 え ら れ た 確 率 の 下 で音 源 の位 置 推 定 値 が 分 布 す る 領 域 を,指 定 し た 検 出SNR,検 出 器 間 隔,相 対 誤 差 の 範 囲 内 で,定 位 可 能 な 音 源 分 布 領 域 と して 導 出 した. 以 上 の よ う な 結 果 を得 た が,こ の 手 法 は,バ イ ス ペ ク ト ル に 始 ま る高 次 ス ペ ク トル解 析 に よ って も,即 実 践 可 能 で あ る. こ の よ う な 統 計 量 の 利 用 に よれ ば,Gauss性 の 雑 音 の 影 響 を うけ な い た め,SNRが 高 い 状 態(50dBな ど)と 同 様 の 精 度 が 期 待 で き る.ま た,検 出 器 を配 置 させ た平 面 と,垂 直 な 方 向 で の 推 定 精 度 が 悪 く な る こ とが わ か っ た が,こ れ は,3点 検 出 法 で は,検 出 器 を平 面 的 に 配 置 させ る た め,伝 搬 距 離 差 お よ び 振 幅 減 衰 差 が,極 め て 小 さ くな る た め で あ る.検 出 器 を 設 置 す る実 質 上 の ス ペ ー ス に制 約 が 無 い な ら,z軸 上 に 検 出 器 を も う1つ 加 え,4点 検 出 とす る こ と に よ り,信 号 を 空 間 的 に と ら え る こ と が 可 能 と な る.こ の こ と に よ り,結 果 的 に 上 記 の 難 点 は 解 消 さ れ る も の と 考 え る.今 後,こ の よ う な 改 良 を 加 え れ ば,本 手 法 は 十 分 に 実 用 可 能 な も の と 考 え ら れ る. 参 考 文 献 1) 岡 田,佐 藤,森 田:3マ イ ク ロ フ ォ ン 系 に よ る3次 元 音 源 定 位 と 音 声 分 離,シ ス テ ム 制 御 情 報 学 会 論 文 誌, 6-3, 149/155 (1993) 2) 安 藤,篠 田,小 川,光 山:時 空 間 勾 配 法 に 基 づ く3次 元 音 源 定 位 セ ン サ シ ス テ ム,計 測 自 動 制 御 学 会 論 文 集, 29-5, 520/528 (1993) 3) 佐 々 木 公 男:検 出 器 の 付 加 的 回 転 を 伴 う 両 耳 聴 取 法 に よ る 近 音 場 定 常 不 規 則 音 源 の3次 元 位 置 推 定,SICE93, 304 M-2, 665/666 (1993)
4) K. Sasaki & K. Uchino: 3D-Biaural Localization of A sta-tionary Random Acoustical Source in Near-Field by Using Amplitude Attenuation of Wave Propagation and An Ad-ditional Rotation of Detectors, Proc. of the 26th ISCIE Int.
Symp. on Stocastic Systems Theory and It's Applications, 161/166 (Institute of Systems, Control and Information Engineers, 1995)
5) K. Sasaki & K. Hirasawa: Biaural Localization of A Sta-tionary Planer Random Acoustical of Wave Propagation, Proc. of the 25th ISCIE Int. Symp. on Stocastic Systems and It's Applications, 75/80 (Institute of Systems, Control and Information Engineers, 1994)
6) G.M. Jenkins & D.G. Watts: Modern Spectral Estima-tion Theory and It's Applications, 412/428, Holden-Day
(1968)
7) H.L. Van Trees: Detection, Estimation and Modulation Theory Part I, 79, John-Wiley (1968)