外れ値検出（知識） script of

取

多変量外れ値

検出取

～

MSD

法

改良手法

い

～

和

美

†

Detection of Multivariate Outliers

取

– Modified Stahel-Donoho Estimators –

WADA Kazumi

外れ値 タヴシ 大部分 傾向 異 る 必 誤り 限ら い タヴシ集計や分析

際 存在 結果を歪

ゆ

う可能性 ある 外れ値 存在 標曓 均や標曓標準偏差 算出 影響

を える れら 値を用い 外れ値検出 検出漏れを起 危険性 高い 取

外れ値 影響を くいュトケダ 単変量 外れ値検出法 代表 序統計量 ある四分 数を用い

る箱 単変量 手法 対象 る変数 変数 関 ある場 外れ値検出 適 い

多変量タヴシ MSD Modified Stahel-Donoho 法 よう 多変量 ュトケダ 外れ値検出法 必要

る

曓稿 統計調査 表業務 る多変量外れ値検出法 適用を目的 干緑緑年 らィヂジ

卸売ン 売業調査 AWRTS 実務 適用 れ MSD法 平00干～平00年 Eurostat 中心

タヴシ゠タ゛ゾ゛ンエ及 補定 新手法 開発ン評価を行 EUREDITプュグゟェダ い 案

れ MSD法 改良版 い 比較評価 実用化 向 考察を行う ある

キヴワヴチ 多変量外れ値検出 射影追跡法 MSD Stahel-Donoho法 SDE

An outlier is a data point which has a different trend from the majority. Though it does not always mean error, its existence may distort the statistics such as the sample mean and the sample standard deviation. Those statistics should not be used as the estimators for the outlier detection since they are not robust.

The most commonly used robust method for the univariate data is the box plot which uses order statistics, however, it does not suitable for the correlated multivariate data. As for the multivariate data, the robust and multivariate method, such as Modified Stahel-Donoho (MSD) estimators, is necessary.

Statistics Canada has adopted the MSD method for the Annual Wholesale and Retail Trade Survey (AWRTS) since 1993. The EUREDIT project, funded by EUROSTAT, proposed a refinement of the method on its report in 2003.

This paper evaluates the MSD method of Statistics Canada and the refined version by EUREDIT aiming for implementation of the multivariate outlier detection for statistical survey data processing at National Statistics Center in Japan. Several topics for practical use are also considered.

Key words: Multivariate Outlier Detection, Projection Pursuit, MSD, SDE (Stahel-Donoho Estimator)

独立行政法人統計コンシヴ る統計調査 表業務 量的変数 関 過去 調

査結果 ら想定 れる正常値 範 を設定 範 ら外れる極端 値を外れ値

検出 いる れ 単変量 外れ値検出法 あり 量的変数 変数 密接 関 あ

る場 単変量 見 場 極端 値 い 変量 関 性 関 大多数 タヴ

シ 傾向 異 る外れ値を検出 る い 属性 よりタヴシを細分化

エャヴプ 正常値 範 を調整 る より 擬似的 よう 多変量外れ値 対応

を行 いる

一方 多変量外れ値検出法 複数 量的変数を同時 り扱い数学的 処理を行う よ

り 極端 値を る単変量 外れ値 加え 関 性 い 外れ値を検出 る ある

取 統計調査 表業務 い よう 多変量外れ値検出法 れ あ り普及 い

カンヌポヴシ 処理能力 飛躍的 向 よう 手法 実用 耐えるよう

ら 曓稿 業務 適用可能性を る を目的 ィヂジ統計局 実用化

れ いるMSD法 改良手法 い 統計サネダR よりプュエメヘ開発を行い 比較評価

を行う ある

第 章 様々 外れ値検出法を り 単変量 手法 多変量 手法 違いや ュトケ

ダ い手法を使 い い を解説 る 第 章 多変量 ュトケダ 外れ値検出

法 ある MSD 法 改良手法 い 概説 第 章 クプポヤヴクミン及 タヴシゾケダ よる比較評価 枠組 を示 第 章 比較評価 結果 い 述 第 章 よう

外れ値検出法を統計調査タヴシ 表業務 利用 る 課題 い 考察 いる

取 多変量外れ値検出 必要性

外れ値検出法 大 く分 単変量 ュトケダ い手法 単変量 ュトケダ 手法

多変量 ュトケダ い手法及 多変量 ュトケダ 手法 種類 分類 る る

れ れ 特徴 以 り

表 取様々 外れ値検出法取

種類 手法 例

単変量 外れ値検出法 取

取 ュトケダ い手法 標曓 均 標曓標準偏差 よる方法

取 ュトケダ 手法 箱 四分 数 よる方法

多変量 外れ値検出法 取

取 ュトケダ い手法

標曓 均 標曓分散ン共分散行列 ら算出 ブデメテニケ 方

距 よる方法

取 ュトケダ 手法

単変量 ュトケダ い手法 標曓 均 標曓標準偏差 よる方法取

取

種類 外れ値検出法 最 一般的 標曓 均をタヴシ 中心 ら

標曓標準偏差 倍以 れ 値を外れ値 る経験的 定方法 ある 取

干.干.干 外れ値検出法 ゾケダ用 よく使用 れるRousseeuw and Leroy 干緑ェウ 星 表面温 対数 密 対数 タヴシコッダ ある Hertzsprung-Russell タヴシを 標準化

変数 プュッダ いる

タヴシを標準化 れ 均 0 標準偏差 干 る タヴシ 正規分布 従う 仮定 る

赤線 示 値 -年 ら 年 範 入る確率 緑緑.緑緑ウ年％ ある 基準 外れ値

存在 い る 取

標曓 均 タヴシ 値を用い 算出 る 少数 極端 値 混入 れ

大 影響を る 標曓標準偏差 標曓 均より 更 大 く外れ値 影響を る

外れ値 検出漏れを起 や い 知られ いる 取

EU域 国 統計部局 中心 り 平00①～平00ウ 実施 れ EDIMBUSプュグゟェダ い 部門横断的 企業調査タヴシ ゠タ゛ゾ゛ンエ及 補定 関 る推奨実践ブッポ゚ャ

Recommended Practices Manual :RPM 作成 れ ブッポ゚ャ 外れ値検出 標曓 均や標曓標準偏差 使用 い 明記 れ いる取ナIstat et al. 平00ウ ん取 林 平00緑 ]取 取 取

取

取

単変量 ュトケダ 手法 箱 取

取

箱 序統計量 ある四分 数 四分 値 を用い 検出法 ある 例え 干00 個

タヴシ ある タヴシを昇 サヴダ る 標曓中央値 イ0 番目 イ干 番目 タヴシ

均 標曓第一四分 数 平イ 番目 平① 番目 タヴシ 均 り 標曓 均や標曓標準偏差 異

り タヴシ 値を用いるわ い 外れ値 影響を くい いう性質 あ

る 干.平.干 箱 概要 堀 中 最 外側 あるタヴシ 置を示 い

る 取

干.平.平 干.干.干 示 よう 標曓 均 ら標曓標準偏差 倍 いう基準 明ら

外れ値 検出 れ Hertzsprung-Russell タヴシを 箱 プュッダ 箱

ィウ 個 タヴシ う 第 変数 個 タヴシ番号 ウん取干干ん取平0ん取年0ん取年ィ 外れ値 検出

れ 取

取

取

干.平.干取外れ値 箱 ［出典 澤 干緑緑平 ］取

取

取

取

取

取

取

取 取

V1

V2

Hertzsprung-Russellタヴシ タヴシフ゜ンダ 固 り ェメケシヴ ら少 れ 幾 タヴシフ゜ンダ 構成 れ いる よう 正常値 ら れ ろ ある外れ値 幾

ある場 標曓 均値 標曓中央値 タヴシ中心を推計 る指標 ある 標曓 均値 標曓中

央値より 外れ値 影響を 外れ値を除い タヴシ 中心より外れ値 多い方向 れる傾

向 あり タヴシフ゜ンダ 散ら りを示 指標 ある標曓標準偏差 標曓四分 差 比較

る 外れ値を除い タヴシより 大 値 りや い 影響 より外れ値 検出漏れ

起 や く 現象 ブケキンエ効果 呼 れる 取

干.平.年 Hertzsprung-Russellタヴシ 標曓 均を橙点 標曓中央値を赤点 標曓 均 標曓 標準偏差 ら計算 れる正常値 範 をベヴグポ 領域 標曓中央値 標曓四分 数 より計算

れる正常値 範 を 領域 示

取

取

取

取

多変量 ュトケダ い手法 標曓 均 標曓分散ン共分散行列 ら算出 ブデメテニ

ケ 方距 よる方法取

取

多変量タヴシ タヴシ 幾 変数を持 タヴシ 外れ いる 比

較 定 る 単一 指標を作る 必要 る マヴェモッチ距 あるい ブデメテニ

ケ距 を算出 る より 多変量タヴシ ら単変量 指標を作り出 る 取

マヴェモッチ距 分 りや く計算 簡単 広く利用 れ いる ブデメテニケ距 変

数間 相関 影響 考慮 れる点 マヴェモッチ距 より 優れ いる 変数相関 0 あれ

ブデメテニケ距 標準化マヴェモッチ距 同 値 ある ブデメテニケ距 値 ある

ブデメテニケ 方距 よる外れ値 定方法 以 り 取

タヴシ数ｎ 変数 数ｐ 多変量タヴシ い ｉ番目 タヴシを

(

,

,...,

)

T

i

x

x

x

x



る

n

i

x

x

,...,

ジヘ 標曓 ある 仮定 各観測値 い (干)式 よりブデメテニケ 方距

(

)

2

i

x

D

算出 る

取 取 取 取 取 取 取 ( ) ( ) ( )

1 2 u x V u x x D i T i

i   



(干)

)

(

2

i

x

D

(

)

)

1

(

)

(

i

D

x

p

n

n

p

n

F







多変量タヴシ 例 Campbell 干緑ェ緑 使用 山火 痕跡を分析 る

を目的 衛星 ら測定 れ 変数 Bushfire 山火 タヴシを使用 る 取

比較 個々 変数 箱 よる外れ値検出を行う 干.年.干 示 よう

第 ン第 変数 個 タヴシ番号 ェん取緑ん取年平ん取年年ん取年ィん取年イん取年①ん取年ウん取年ェ 単変量外れ値

検出 れる れら 単変量外れ値を示 散布 行列 干.年.平 行 標プュッダ 干.年.年

ある い れ 箱 検出 れ 単変量外れ値を赤 表示 いる 取

V1

80 120 160 150 250 350

80 1 10 140 80 12 0 16 0

V2

V3

V4

80 100 120 140 0 200 400 200 250 300 350

2

00

300

V5

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

取

Bushfireタヴシ い 算出 ブデメテニケ 方距 をプュッダ 干.年.ィ あ

る 検定統計量F 緑イ％値を点線 緑緑％値を実線 表示 いる 緑イ％値を基準 ブ

ケキンエ効果 外れ値 検出 れ い 取

干.年.平取散布 行列 Bushfireタヴシ取ナ年ェ×イ 変数]取

0 10 20 30

0

5

1

0

15

20

距離プ ロッ

［

Bushfire

ー タ］

ータ番号

ラ

ビ

ス

平

方距離

％点

99

％点

95

箱ひげ図 よ 正常値

箱ひげ図 よ 外 値

取

多変量 ュトケダ 手法 MSD法

取

多変量 検出手法を用い れ ュトケダ れ ブケキンエ効果 よる外れ

値 検出漏れ 起 りや い 多変量 ュトケダ 外れ値検出法 必要 あり 近

様々 手法 案 れ いる 第 章 述 るModified Stahel-Donoho MSD 法を り る 取

干.ィ.干 Bushfireタヴシ い MSD法 より外れ値検出を行 結果を 行 標プュ

ッダ 示 赤線 示 箱 よる外れ値 個々 変数 極端 値を るタヴシ

ある 一方 MSD法 検出 れる 箱 検出 れる単変量外れ値 加え 変数

見 必 極端 値 ら い 変数間 関 性 タヴシ 大部分 違う傾向を持

よう 線 示 外れ値 ある 特徴 ある 取

干.ィ.平 MSD法 よりュトケダ 推計 れ ブデメテニケ 方距 プュッダ 箱 外れ値 箱 検出 れ い外れ値を同 よう 色分 表示 いる 取

取

取

取

取

取

取

取

0 10 20 30

0

50

1

00

1

50

2

00

2

5

0

距離プ ロッ

［

Bushfire

ー タ］

ータ番号

法

よ

ロ

ス

ラ

ビ

ス

平

方距離

MS

D

％点

99.9

％点

99

正常値

箱ひげ図でもMSD法でも検出さ 外 値 法でしか検出さ い外 値

MSD

干.ィ.干取 行 標プュッダ Bushfireタヴシ取ナ年ェ×イ 変数]取

3.5 4.0 4.5 5.0 3

4 5 6

点 95%

点 99%

点 99.9%

法の ータ中心 MSD

点 95%

点 99%

点 99.9%

中央値

平均 中央値

平均

点 95%

点 99%

点 99.9%

法の ータ中心 MSD

点 95%

点 99%

点 99.9%

単変量 手法 い り 第 節及 節 使用 変数 Hertzsprung-Russell タヴシ い 多変量 手法を適用 結果を 干.ィ.年 示 干.平.年 同様 標曓 均

標曓標準偏差 ら計算 れる正常値 範 をベヴグポ 領域 標曓中央値 標曓四分 数 より

計算 れる正常値 範 を 領域 示 ら ュトケダ い通常 方法 推計 ブデ

メテニケ 方距 よる正常値 範 をアヤング線 MSD法 よりュトケダ 推計 ブデメテ ニケ 方距 よる正常値 範 を赤線 示 いる 取

変数 場 単変量 手法 よる正常値 範 矩 く

形 る 対 多変量 手法 よる

正常値 範 楕 形 る 単変量ン多変量い れ 場 ュトケダ い手法 外れ

値 存在 る 影響 正常値 定 れる領域 広 う 取

取

取

取 Modified Stahel-Donoho MSD 法 改良手法 い

取

取

基礎 る手法

取

Stahel 干緑ェ干 及 Donoho 干緑ェ平 案 SD法 タヴシを様々 方向 直線 射影

直線 る中心 ら

い

よ 各タヴシフ゜ンダ ゞ゠゜ダを付 る

より 均値ベェダャ 分散ン共分散行列をュトケダ推定 る 破壊点 高い り多く 外

れ値 混入 耐える手法 ある 取

Patak 干緑緑0 SD 法 よりュトケダ推定 れ 分散ン共分散行列を用い 主成分分析を 案 ィヂジ統計局 れを用い 破壊点 約 0.イ 理論的 イ0％近い外れ値 混入 耐える

高く 直交変換 変 多変量外れ値検出法を実現 ［Franklin and Brodeur 干緑緑ウ ］ ら

EUREDITプュグゟェダ ィヂジ統計局 手法 改良法 案 れ いる取ナBéguin and Hulliger 平00年 ] 取

EUREDITプュグゟェダ［http://www.cs.york.ac.uk/euredit/］ Eurostat 資金 供 タヴシ゠ タ゛ゾ゛ンエ及 補定 新手法 開発ン評価を行う を目的 EU 域 国 統 計部局や大学 研究者 参加 平00干～平00年 実施 れ 取

取

取

MSD法 概要

取

タヴシを様々 方向 直線 射影 る より 分布 端 方 ある外れ値 候補

を見付 各タヴシ 一 ゞ゠゜ダ 付 を行う 分布 中心部 近い ろ あるタヴシフ゜

ンダ ゞ゠゜ダを 干 れ ろ あるタヴシフ゜ンダ 干 より いゞ゠゜ダを付

る より タヴシ 影響を弱 り あるい ゞ゠゜ダを 0 影響を排除

り る る 取

一 ゞ゠゜ダを用い タヴシ 中心を示 均値ベェダャ 散ら りや相関を示 分散ン

共分散行列を計算 る より 外れ値 影響を くい一 推計値を求 る 取

う 得られ 分散ン共分散行列を固暼値分解 る より 主成分分析を行う

主成分分析自体 ュトケダ 手法 く外れ値 影響を や い タヴシ ゞ゠゜ダ付

求 分散ン共分散行列を用いる よ ュトケダ 分析 可能 る 取

第一主成分 分散 最 大 く るタヴシ 射影方向を示 ベェダャ る れ 言わ

タヴシ 最大 類似成分を示 方向 ある 第 主成分 タヴシ ら第一主成分 表 れる成

分を り除い 後 同様 分散を最大化 る方向を示 ベェダャ り 第 主成分 タヴシ

ら第一ン第 主成分 要素を り除い 後 同様 分散を最大化 る方向を示 ベェダャ る

り 第一主成分 タヴシ 類似性を代表 る 第 主成分以降 類似性より 非類似性

集約 れ いく 外れ値検出 関 暼用性 高い 固暼値 値 わら 算

出 れる 固暼ベェダャを使用 再 射影を行い ゞ゠゜ダを精緻化 る より

更 精 高い 均値ベェダャ 分散ン共分散行列 最終推計値を求 る 取

外れ値 定 均値ベェダャ 分散ン共分散行列 最終推計値を用い ブデメテニ

ケ 方距 を算出 る 検定統計量Fを目安 ブデメテニケ 方距 大

りタヴシ中心 ら一定基準以 れ ろ ある 定 れ タヴシフ゜ンダを外れ値

検出 る

基 く改良版 EUREDIT版 違いを検証 る 統計サネダR 開発 MSD法プュ エメヘ 処理概要 ある 取

サヴケ及 実行カヴチ 紙 示 同 プュエメヘ 制御ドメベヴシ よりィヂジ版

EUREDIT版 処理を行う る 様 いる

取

(干)取タヴシ 中心化取

最終的 分散ン共分散行列 均値ベェダャ 原点 り方 結果 変わら いよう 取

1

L

取

取 取 置Ｔ

1

L

取

通常 中心 ら各タヴシフ゜ンダ マヴェモッチ距 和 最 るよう 推計

量を用いる 場 中心 ら遠いタヴシフ゜ンダ 中心 推定値 える影響 大

く る れを避 る 距 絶対値 和 最 るよう 推計値を使用 いる

Béguin and Hulliger 平00年 後 処理 原点 変 中心化 必要 い 指摘 り 実際 検証を行 結果 変わら い を確認 後 ィヂジ版 い プュエメヘ

ら 当ケゾップを削除 取

取

(平)取一 ゞ゠゜ダ 算出取

一定 数 メンジヘ 直交基底を作成 基底を構成 る各基底ベェダャ 張る直線 タ

ヴシフ゜ンダを射影 線 中心 ら 距 残差 を求 残差 大 より

一 ゞ゠゜ダを設定 る 取

取

ン取 直交基底 作成取

変数 数をp る p個 要素を持 直交ベェダャp個 一組 直交基底を構成 る 基底数をb る b×p×p個 一様乱数を作り p個 要素を持 ベェダャをb×p個 発生 る ベェダャp個 エメヘンクポプッダ 直交化を行い b組 直交基底 を作成 る

Franklin and Brodeur 干緑緑ウ い 変数当 り 直交基底数 最 干0 いる ィヂジ版 基底数 変数当 り 干0 取

EUREDIT 版 基底数 Maronna and Yohai 干緑緑イ 従い 変数当 り

exp(2.1328+0.8023p)/p 基底数 元数 増加 従い指数関数的 大 く る

表 平.平.干取基底数 射影数 違い取

変数の数p 2 3 4 5 6 7 8 9 10

1変数当たり

の基底数

カナ 版 10 10 10 10 10 10 10 10 10

EUREDIT版 41 93 208 466 1039 2319 5172 11539 25739

総射影数 基

底ベク ル数

カナ 版 20 30 40 50 60 70 80 90 100

EUREDIT版 82 279 832 2330 6234 16233 41376 103851 257390



n

i i

T ₁||x T||

平.平.干取変数 数 総射影数取

取

取

取

取

取

取

取

取

取

取

取

取

取

ン取 直交基底 射影

j番目 基底ベェダャ

j

v 1≤j≤p 張る直線 各タヴシフ゜ンダ

i

z

ダャ 垂線を ろ 射影ベェダャ 長

i T

j

z

v

取 取 平.平.平取射影 ゜ベヴグ 取

ン取 残差 算出

射影ベェダャ 長

i T

j

z

v

残差

ij

r

値 る 中央絶対偏差 各タヴシフ゜ンダ ら標曓中 数を引い 値 中央値 ある 取

med 中 数 median 取

ン取 残差 刈り込

ィヂジ版 以 基準 刈り込 残差

ij

r

~

を算出 る 元 分布 正規分布 ある

仮定 場 刈り込 前残差

ij

r

従う 干.ウイ 緑干.緑緑％点 年.イ 緑緑.緑イ％点 当 る 取

取

取

取

取

取

EUREDIT版 式 より変数 数p よ 刈り込 開始 置を変え 刈り込 残差

ij

r

~

を算出 る 取

取

取

取

取

取

取 取 取 取 平.平.年取 残差 ゞ゠゜ダ 関 取 取 平.平.ィ取 変数 よる刈り込 基準 変化取

取 取

ン取 一 ゞ゠゜ダ算出

ィヂジ版 EUREDIT 版 式 よう 刈り込 残差

ij

r

~

を刈り込 前残差

ij

r

元 ゞ゠゜ダ

ij

w

あるタヴシフ゜ンダ ゞ゠゜ダ 干 る 刈り込 大 いタヴシ 中心部 ら遠いタ

ヴシフ゜ンダ ゞ゠゜ダ く る 取

ij ij

ij

r

r

w



~

/

          ij ij ij ij ij r if r if r if r r 5 . 3 0 5 . 3 75 . 1 75 . 1 75 . 1 ~





95 . 0 , 2 / 0 ~ p ij ij ij ij ij c r c if r c c r if r

r 



式 よう b組 直交基底 元 ゞ゠゜ダ 積和

i

w

シフ゜ンダ 全基底を通 最 ゞ゠゜ダを選 れを一 ゞ゠゜ダ る

平.平.イ取メンジヘ 直交基底 射影 よる一 ゞ゠゜ダ算出取

取

取

(年)取ゞ゠゜ダ付 主成分分析取

一 ゞ゠゜ダを用い 均値ベェダャ

u

ˆ

V



を推計 得られ 分散ン共

分散行列

V



ら固暼値 固暼ベェダャを求 る より ュトケダ 主成分分析を行う 取

取

取 均値ベェダャ

分散ン共分散行列

取

(ィ)取最終ゞ゠゜ダ 決定取

主成分分析 よりp変数タヴシ あれ p個 要素を持 固暼ベェダャ p個算出 れる

れ 作成 b組 直交基底 同様 一組 直交基底 る れら

ij ij p j

i

r

r

w





~

/

固暼ベェダャ タヴシを射影 残差 算出ン標準化ン刈り込 及 元 ゞ゠゜ダ 積和算

出 より ゞ゠゜ダを作成 る

ィヂジ版 場 ゞ゠゜ダを 最終ゞ゠゜ダ 用 EUREDIT 版

一 ゞ゠゜ダ ゞ゠゜ダをタヴシフ゜ンダ 比較 い方を最終ゞ゠゜ダ

る 取

取

(イ)取ブデメテニケ 方距 算出取

最終ゞ゠゜ダを用い 再 分散ン共分散行列 均値ベェダャをュトケダ推計 れら

値 ら 式 よりブデメテニケ 方距 取

(

)

2

i

x

D

取

取

取

(①)取外れ値 特定取

ブデメテニケ 方距 取

(

)

2

i

x

D

i

F

い 式 より求 る る

外れ値 定 る検定統計量

i

F

値 取

取

)

(

)

(

)

(

u

x

V

u

x

x

D







)

(

)

1

(

)

(

i

D

x

取 クプポヤヴクミン タヴシゾケダ

比較方法

ィヂジ 卸売ン 売業調査 AWRTS タヴシン゠タ゛ゾ゛ンエ業務 適用 れ MSD

法 ィヂジ版 EUREDITプュグゟェダ 案 れ MSD法 改良版 EUREDIT版 い 比較評価を行う 取

れら 版 細 い 第 章 述 相違点 射影 変数当 り

基底数及 射影 残差 よるゞ゠゜ダ 付 方 ある れ れ 効果を確認 る

点 列組 る以 通り 比較条件を設定 クプポヤヴクミン及 タヴシゾケダ

を行 取

取

表 年.干.干取比較条件取

クプポヤヴクミン

Maronna and Yohai 干緑緑イ 及 Peña and Prieto 平00干 外れ値検出 いクプポヤヴクミ ンタヴシ ュトケダ 多変量外れ値検出法 評価 式 形 タヴシを使用 いる α

外れ値割 p 変数 数 λ 外れ値 分散 δ 正常値 ら 外れ値 距 あり 正常値 タヴシ総数×(1 α)個 原点中心 分散ン共分散行列I p 元正規分布乱数 外れ値 タヴ シ総数×α個 均 0 分散λ 正規分布 従う乱数を第一軸 原点 ら距 δ 加え

る

)

,

(

)

,

0

(

)

1

(





N

I





N



e



I

タヴシ 正常値 外れ値 れ れ正規分布 従う 実際 統計調査タヴシ 場

分布 れい 形 る 限ら い 歪 ゆ

ん 分布あるい 厚い分布 程 対応 る

を確認 る 曓研究 正常値 正規分布 加え Skew-T分布 複 フワサン分布及

対数正規分布 従う擬似乱数タヴシを使用 年.平.干 及 年.平.平 れら 分布 密

関数をプュッダ 各ドメベヴシ 値 タヴシ設計 細 紙 示 取

取

取

タヴシゾケダ取

取

タヴシゾケダ クプポヤヴクミンタヴシより 実タヴシ 近く 多変量外れ値検出法 性

能評価 よく使用 れるタヴシコッダを中心 選択 細 紙 り 取

取

基底数 ゞ゠゜ダ付

ィヂジ版 ィヂジ版 ィヂジ版

ィヂジ基底増加版 EUREDIT版 ィヂジ版

EUREDIT版 EUREDIT版 EUREDIT版

年.平.干取正規分布及 Skew-T分布 密 関数

年.平.平取正規分布 複 フワサン分布及 対数正規分布 密 関数

0 2 4 6 8 10

0

.0

0

.2

0

.4

0

.6

0

.8

1

.0

0 2 4 6 8 10

0

.0

0

.2

0

.4

0

.6

0

.8

1

.0

0 2 4 6 8 10

0

.0

0

.2

0

.4

0

.6

0

.8

1

.0

正規分布

複合 ワソン分布

取 結果

クプポヤヴクミン 結果

MSD法 組 射影数 増える 検出率 高く る 回行 クプポヤヴク ミン 射影数 違い よる検出率 差 明確 見られ い れ 回作成 擬似乱

数 よるクプポヤヴクミンタヴシ 射影数 よる検出力 差 明ら 出る 十分 易

高い 考えられる 取

ゞ゠゜ダ付 い 検出率 明確 差異 現れ い い ィヂジ版及 ィヂジ基底増加

版 い 途中 計算 能 り外れ値検出 い場 ある 計算 能 るタヴ

シ条件 表 ィ.干.干 り 干0 変数 変数間相関 高く く 標準偏差 い外れ値 ィ0％

多く 正常値 外れ値 間 タヴシフ゜ンダ 全く い空間 る ィ.干.干 よう 状況

起 や い タヴシフ゜ンダ 最終ゞ゠゜ダ 0 0 近い値 り

最終分散ン共分散行列 正定値 く る ブデメテニケ 方距 算出 分散ン共分散行列

逆行列 必要 外れ値検出 い 計算 破綻

ん

い いう点 EUREDIT 版 ゞ゠゜ダ関数 ィヂジ版より優れ いる いえる

取

取

表 ィ.干.干取外れ値 検出 能 る 取

条件 正常値の分布

自由 度

相 関

歪 み

外れ値 標準偏

差

距 離

変 数

外れ 値割 合

カナ 基底増加版 正規分布 - 0 - 0.1 100 10 40

カナ 基底増加版 正規分布 - 0.4 - 0.1 100 10 40

カナ 基底増加版 対数正規分布 - 0 - 0.1 100 10 40

カナ 版 カナ 基底増加版 Skew-T分布 10 0 5 0.1 10 10 40

カナ 版 カナ 基底増加版 Skew-T分布 10 0 10 0.1 10 10 40

カナ 版 カナ 基底増加版 Skew-T分布 Inf 0 1 0.1 10 10 40

カナ 版 カナ 基底増加版 Skew-T分布 Inf 0.4 5 0.1 10 10 40

カナ 基底増加版 Skew-T分布 10 0 1 0.1 100 10 40

カナ 基底増加版 Skew-T分布 10 0 5 0.1 100 10 40

カナ 基底増加版 Skew-T分布 10 0 10 0.1 100 10 40

カナ 基底増加版 Skew-T分布 Inf 0 0 0.1 100 10 40

カナ 基底増加版 Skew-T分布 Inf 0 1 0.1 100 10 40

カナ 基底増加版 Skew-T分布 Inf 0 10 0.1 10 10 40

カナ 基底増加版 Skew-T分布 Inf 0 5 0.1 100 10 40

カナ 基底増加版 Skew-T分布 Inf 0 10 0.1 100 10 40

カナ 基底増加版 Skew-T分布 Inf 0.4 0 0.1 100 10 40

カナ 基底増加版 Skew-T分布 Inf 0.4 1 0.1 100 10 40

カナ 基底増加版 Skew-T分布 Inf 0.4 5 0.1 100 10 40

カナ 版 Skew-T分布 10 0.4 5 0.1 10 10 40

カナ 版 Skew-T分布 Inf 0 5 0.1 10 10 40

クプポヤヴクミン 結果 細 正規分布タヴシ い 表 Skew-T分布タヴシ い 表 複 フワサン分布タヴシ い 表 対数正規分布タヴシ い 表 示

れら 表 い 計算 能 起 箇所 誤検出率ン漏れ率ン検出率

表記 いる 取

取

取

ィ.干.干取外れ値 検出 能 るクプポヤヴクミンタヴシ例取

タヴシゾケダ 結果

(干)取Hawkins-Bradu-Kaasタヴシ取

変数タヴシ 元プュッダを ィ.平.干 示 ィ.平.平 変数 う 特徴

分 りや い第 変数 第 変数をプュッダ いる れ 外れ値 目視 明ら

ュトケダ いブデメテニケ 方距 外れ値検出を試 る 検定統計量F 緑イ％値を基

準 確率楕 ィ.平.平 点線 一番 側 赤 示 外れ値 検出

い 示 タヴシ中心 実際より いぶ外れ値側 寄り 外れ値 影響 分散 大

く る 正常値範 を示 楕 広 う 原因 ある 取

一方MSD法 い ィ.平.平 ィヂジ版 赤 EUREDIT 版 青 違い ん く 両者 正常値 均値ベェダャ 分散ン共分散行列を推計 いる 分

る 取

取

(平)取ケ゜ケ ヤケダメン業タヴシ取

変数タヴシ 散布 ュトケダ いブデメテニケ 方距 ィヂジ版及

EUREDIT 版 よる確率楕 を い を ィ.平.年 示 検出 れる外れ値 若 違

い 出る 実質的 ん 手法 よる差 い る 取

外れ値 正常値 近接 り 正常値 比較 外れ値 数 少 い場 ュトケダ

ィ.平.干取 Hawkins-Bradu-Kaasタヴシ取 取取 ィ.平.平取 Hawkins-Bradu-Kaasタヴシ

Ｄプュッダ 取 ブデメテニケ距 楕

取 取

取

取

取

取

(年)取Hertzsprung-Russellタヴシ取

第 章 り 変数 タヴシコッダ ある 散布 各手法 よる確率楕 をプュ

ッダ を ィ.平.ィ 示 射影数 多寡 よる差異 ん い ゞ゠゜ダ付

違い より確率楕 形 大 く変化 り ュトケダ い通常 ブデメテニケ距 や

ィヂジ版より EUREDIT版 確率楕 方 正常値 分布 形 沿う 分 る

(ィ)取Bushfire 山火 タヴシ取

第 章 り 変数タヴシ 複数回検出を行 結果 安定 いる EUREDIT

版 あ 取

外れ値を色分 散布 行列を ィ.平.イ 示 EUREDIT版 検出 る 干平 個 外れ値

う 箱 検出 れる単変量 外れ値を赤 箱 検出 い MSD 法 検

出 る 個 外れ値を 表示 いる ィ.平.① 同 を 行 標プュッダ 示

いる 干.ィ.干 同 ある 取

取

取

取

取

取

ィ.平.イ取 Bushfireタヴシ散布 行列

(イ)取Stacklossタヴシ

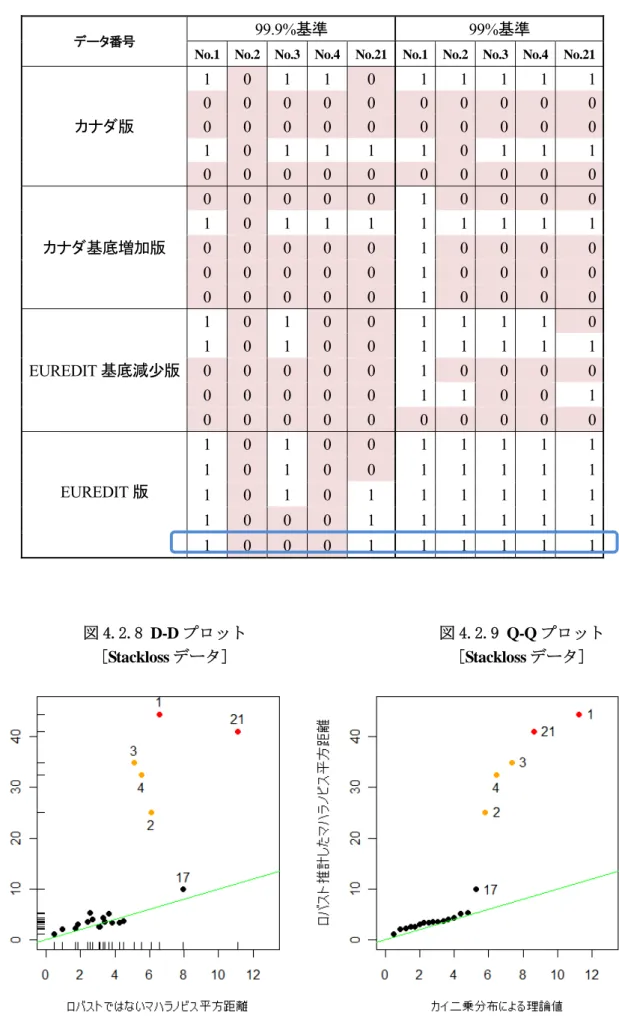
タヴシコッダ 外れ値 タヴシ番号No.干ん取平ん取年ん取ィん取平干 ある 分 いる

乱数を変え 回 検出を行 外れ値 定基準を検定統計量F 緑緑.緑％値 る 条件 結果 安定 い 取

基準を緑緑％値 ろ EUREDIT版 回 正 い外れ値を検

出 表 ィ.平.干 外れ値 い 検出結果を示 り 0 正常値 干 外れ

値 いう 定 ある タヴシフ゜ンダ以外 正常値 定 れる 取

ィ.平.ウ タヴシ 散布 行列 表 ィ.平.干 青い四角 ん 部分 試行 際

緑緑.緑％基準 検出 れ 外れ値 あるNo.干 平干 を赤 緑緑％基準 検出 れ 外れ値 ある

No.平ん取年ん取ィを橙 表示 いる ィ.平.ェ ィ.平.緑 同 試行 際 D-Dプュッダ Q-Q プュッダ ある D-Dプュッダ Q-Qプュッダ タヴシ 同 分布 従 いれ 示

原点を通る傾 干 直線 タヴシフ゜ンダ る

取

取

Air.Flow

18 20 22 24 26 10 20 30 40

50

60

70

80

18

20

22

24

26

_Water.Temp

Acid.Conc.

75

80

85

90

50 60 70 80

10

20

30

40

75 80 85 90

表 ィ.平.干取Stacklossタヴシ検出結果

番号

99.9%基準 99%基準

No.1 No.2 No.3 No.4 No.21 No.1 No.2 No.3 No.4 No.21

カナ 版

1 0 1 1 0 1 1 1 1 1

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

1 0 1 1 1 1 0 1 1 1

0 0 0 0 0 0 0 0 0 0

カナ 基底増加版

0 0 0 0 0 1 0 0 0 0

1 0 1 1 1 1 1 1 1 1

0 0 0 0 0 1 0 0 0 0

0 0 0 0 0 1 0 0 0 0

0 0 0 0 0 1 0 0 0 0

EUREDIT基底減少版

1 0 1 0 0 1 1 1 1 0

1 0 1 0 0 1 1 1 1 1

0 0 0 0 0 1 0 0 0 0

0 0 0 0 0 1 1 0 0 1

0 0 0 0 0 0 0 0 0 0

EUREDIT版

1 0 1 0 0 1 1 1 1 1

1 0 1 0 0 1 1 1 1 1

1 0 1 0 1 1 1 1 1 1

1 0 0 0 1 1 1 1 1 1

1 0 0 0 1 1 1 1 1 1

ィ.平.ェ取D-Dプュッダ

ナStacklossタヴシ]取

ィ.平.緑取Q-Qプュッダ

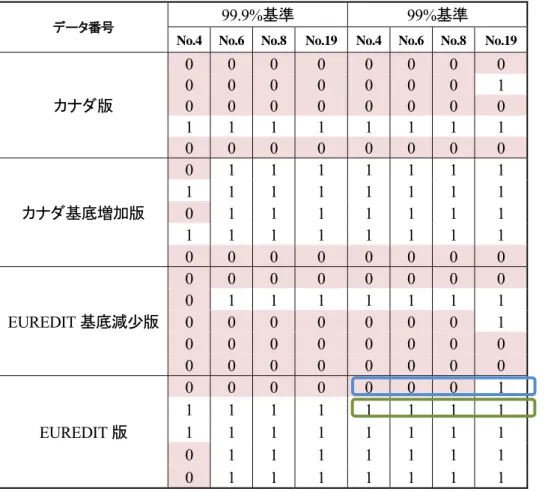
(①)取Modified Wood Specific Gravityタヴシ

タヴシコッダ 外れ値 タヴシ番号No.ィん取①ん取ェん取干緑 ある 分 いる 取 外れ値 定基準を検定統計量F 緑緑.緑％値及 緑緑％値 乱数を変え 回 検出 を行 結果 表 ィ.平.平 り 取

射影数 多いィヂジ基底増加版 EUREDIT 版 結果 明ら 良い ら 条件

回 う 回 検出漏れを起 タヴシフ゜ンダ以外 条件

正常値 定 れる 取

表 ィ.平.平 青 四角 ん 部分を れ れ試行A 試行B る 試行A 検 出漏れ 起 いる 試行B 外れ値を正 く検出 いる ィ.平.干0

試行 D-Dプュッダ及 Q-Qプュッダを対比 れ れ 試行 検出 れる外 れ値を赤 示 ィ.平.干干 散布 行列 試行A B 検出 れるNo.干緑 を 赤 試行A 検出 れ い 試行B 検出 れるNo.ィん取①ん取ェ を橙 示 いる 取

取

取

表 ィ.平.平取Modified Wood Specific Gravityタヴシ検出結果

番号

99.9%基準 99%基準

No.4 No.6 No.8 No.19 No.4 No.6 No.8 No.19

カナ 版

0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 1

0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0

カナ 基底増加版

0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0

EUREDIT基底減少版

0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1

0 0 0 0 0 0 0 1

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

EUREDIT版

0 0 0 0 0 0 0 1

1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1

A

ィ.平.干0取D-Dプュッダ Q-Qプュッダ取ナModified Wood Specific Gravityタヴシ]

試行A D-Dプュッダ

試行B D-Dプュッダ

試行A Q-Qプュッダ

結果 取

取

クプポヤヴクミン及 タヴシゾケダ結果 ら 回ゾケダを行 表 年.干.干 示 条

件 う EUREDIT版 最 優れる いえる

MSD法 残差 刈り込 正規分布 仮定を置くドメベダモッェ 手法 あり タヴ シ 正規分布 ら遠く れ 検出力 落 る 射影時 乱数を使用 いる 易

高いタヴシ 場 外れ値検出 結果 安定 い あり 複数回 検出実行や 手法

取 考察

ィヂジ統計局 実用化

Béguin and Hulliger 平00年 よれ Franklin and Brodeur 干緑緑ウ 紹 れ いるィヂジ統

計局 卸売ン 売業調査 AWRTS MSD法 適用 各国統計部局 る多変量

外れ値検出法実用化 唯一 例 ある

AWRTS 卸売ン 売業 基礎統計収集を目的 層 単純メンジヘ抽出 標曓抽出

行われ 干緑緑イ 調査時点 標曓規模 約平ウん000社 大 い プェュ゠タ゛ゾ゛ンエ 負担を

軽減 る スゟッェ前 タヴシ 干緑緑年 らMSD法 適用 れ いる 検出 れ 外れ値 ホッダタッェ法 補定を行う チヂヴや 均値補定を行う 均値算出 補定 関

る処理 ら 除外 れる 外れ値検出 省力化 加え タヴシ品質向 貢献

いる 考えられる 取

卸売ン 売 スゟヴン 否 会社規模 大ン中ン 商業エャヴプ より区分 れ 補

定 チベ゜ン 層 よりタヴシを細分化 数百あるチベ゜ン 数量 目 関

MSD 法 よる多変量外れ値検出を行 いる 対象 る数量 目 期首棚卸高 期曒 棚卸高 総支出 商品原価及 賃金ン福利厚生費 ある タヴシ分布 対称性を確保 る

数量 目 い 営業収入 比を り 期首棚卸高及 期曒棚卸高 い 対数変

換 行われる

外れ値検出プュエメヘ C言語 開発 れ 人手 よる審査 作業量をカンダュヴャ る 検出 る外れ値数を制限 る機能を持 検出 れ 外れ値 ブデメテニケ 方距 最 寄

変数を手掛 り 審査 れる

Franklin and Brodeur 干緑緑ウ 干緑緑イ 実績 検出 れ 外れ値 全体 ィ％ う タヴシ修正を行う誤タヴシ 全体 割 タヴシ修正を行わ い特異値 残り 割 あ

述 いる 取

統計調査タヴシ 適用 向

ュトケダ 多変量外れ値検出法 手法を選 検出率 よう 程 い

う 加え 調査 目を対象 よう 適用 る いう 重要 る 曓

節 ィヂジ統計局 例を踏 え 実用化 向 考慮 幾 い 考察を

行う

(干)取変数 選択取

必要 変数を見落 外れ値 検出 い 一方 調査 目を 検

出を行う カンヌポヴシ処理 観点 ら 検出精 観点 ら 現実的 い 取

一般 ュトケダ 多変量外れ値検出法 タヴシ処理 負荷 高い MSD法 場 特 射影数 多く る 処理時間 増え 使用ベペモ 増大 る い 対象 る変数

を削る 実用 重要 ある 加え 対象 る変数 多い場 検出 れ 外

れ値 審査 負担 増える 変数間 何ら 関 性 ある を選 対

れ値 検出 る ある 変数 極端 値を る 変数 全体 傾向 ら外れ

い いよう 単変量外れ値 対象変数 多い 検出 れ くく る傾向を持

紙 調査票を見る限り AWRTS 調査 れ いる数量 目 対象 変数より 多く 何ら 基準 対象 る変数を 絞 いる 思われる 取

取

(平)取ィゾガモ 目 処理取

MSD法 多変量外れ値検出法 数量 目を対象 いる 通常統計調査タヴシ ィゾガモ 目 数量 目 混在 る 外れ値検出 対象 る数量 目 影響

あるィゾガモ変数を 選ん ェュケ集計を行い エャヴプ タヴシ る 単一

分布 るようタヴシを細分化 エャヴプ 外れ値検出を行わ れ ら い

AWRTS 場 補定 チベ゜ン 層 を使用 いる

取

(年)取 測値 対応取

Franklin and Brodeur 干緑緑ウ 及 Béguin and Hulliger 平00年 よるMSD法自体 測値

対応 い い AWRTS 対象変数 数を変え 繰り返 外れ値検出を行う

より 測 あるタヴシ値 適用を行 いる

AWRTS 対象 る 変数 う 測 ある 期首棚卸高 期曒棚卸高 ある

対象変数 測 いタヴシ い 変数 期首棚卸高を除い 変数 期首棚

卸高ン期曒棚卸高を除い 変数 いう形 回外れ値検出を繰り返 いる 取

取

(ィ)取タヴシ変換 い

MSD法 ュトケダ 手法 タヴシを対称 正規分布 仮定 り AWRTS

タヴシ分布 対称性を確保 る 変数 を営業収入 比率 期首棚卸

高及 期曒棚卸高 対数変換 行 いる 取

対称分布 仮定を置く手法 い タヴシ 対称性 問題 ある場 対数変換を

含 Box-Cox変換 タヴシを正規分布化 る前処理 行われる 多い う

変換 より 特 正常値 近接 り分散 正常値より 大 外れ値 検出 くく

る 注意 必要 ある 取

イ.平.干 クプポヤヴクミンゾケダ 使用 対数正規分布タヴシ よる 対数変換

例 ある 正常値 変数 相関 あり標準偏差 干 原点を中心 る多変量正規分布タヴ

シを指数化 外れ値 A 標準偏差イ B 標準偏差0.干 正規分布タヴシ を 第一軸 原点 ら距 干0 れ ろ 加え いる 外れ値 標準偏差 大 い A

場 外れ値 標準偏差 いB 比較 る 変換前 り正常値 外れ値 混 いる 変換 より更 正 い外れ値 検出 困 る 分 る 取

一般 ゴュや負 数 ある場 タヴシ 正 数 るよう 行移動

らBox-Cox変換を行う Box-Cox変換 行移動 変 い り 程 動

より外れ値検出 結果 変化 う

(イ)取人 よる審査 必要性

検定統計量F 緑緑.緑％点 いうMSD法 外れ値検出基準 飽く 目安 あり 第 章 り StacklossタヴシやModified Wood Specific Gravityタヴシ 検出例 よう

回 検出 実行や 多変量外れ値検出法 併用を行う 幾 異 る結果 得られ

る場 あり 最終的 結果 正 い 調査タヴシ 関 る知見を持 人間 総

的 断 る必要 ある

AWRTS 検出 外れ値 人 審査 いる 検出プュエメヘ チベ゜ン 検出

れる外れ値 数を制御可能 外れ値検出基準 調整 る 様 ある 検出法 ィヂジ

版 MSD法 を使用 検出 回 外れ値 少 く分布 比較的正規分布 近い れ 検出 易 高く い 問題 起 くい 思われる 取

わり

曓稿 り MSD法 よう ュトケダ 多変量外れ値検出法 特定 変数 必 極端 値を ら い 変数 関 性 ら見る 大部分 タヴシ 傾向 異 るよう 外れ値

を検出 る る 特徴 ある 取

統計調査 表業務 い 集計表 最終成果物 ある場 個々 タヴシ 変数 調査

目 間 関 性 情報 ん 残ら い よう 外れ値検出 必要性 高く い

統計タヴシ 利用 進を る新 統計法 成 平干 暻 ら全面施行 れ 個 タヴシ 供

可能性 拡大 取

集計表 異 り 個 タヴシ 変数間 関 性 保持 れ り 利用者 よう

関 性 分析を目的 個 タヴシを利用 る 多い MSD法 よう 多変量外れ 値検出法 暼効 る可能性 ある

後 回評価用 作成 MSD 法プュエメヘを大規模タヴシ 対応 るよう改良を 行う MSD法以外 外れ値検出法 含 ベンスブヴキンエを行い 実用化

イ.平.干取外れ値を含 対数正規分布タヴシ 対数変換 影響取

A.外れ値 分散 大 い場

紙 取 外れ値検出プュエメヘ取

################################################################### # 取 取 取 取 取取 取 MSD法多変量外れ値検出関数 Ver. 1.6 09/07/14取

###################################################################

####### ィヂジ版 EUREDIT版 比較評価用

####### 対応 るタヴシ 大 ン 元数 ベペモ 依存 る

####### 外れ値検出タヴシを゜ンプッダ える ュトケダ推計 均値ベェダャ 共分散行列を計算 る

###################################################################

####### 関数msd ドメベヴシ一覧

#######

####### inp 必須 外れ値検出を行い いn×p タヴシ行列

####### 取 以 ドメベヴシ 省略可能 タネァャダ EUREDIT版 設定

####### sd 乱数 クヴチ 再現性 必要 場 指定(0 回違う再現 能 乱数)

####### nb 基底数カンダュヴャ用 1 元当 り 基底数を設定 る

####### tm "CAN" ィヂジ版 "EUR" EUREDIT版 よるゞ゠゜ダ 刈り込 を行う

###################################################################

####### 関数msd取 戻り値一覧

#######

####### u1 一 ゞ゠゜ダ より推計 れ 均値ベェダャ

####### V1 一 ゞ゠゜ダ より推計 れ 共分散行列

####### bwt 一 ゞ゠゜ダ

####### u2 最終 均値ベェダャ

####### V2 最終共分散行列

####### wts2 最終ゞ゠゜ダ

####### eg 一 ゞ゠゜ダ より推計 れ 共分散行列 固暼値

####### ctb 一 ゞ゠゜ダ より推計 れ 共分散行列 固暼ベェダャ

###################################################################

msd <- function(inp, nb=0, sd=0, tm="EUR") {

inp_d <- ncol(inp) # 元数

inp_n <- nrow(inp) # タヴシ数

###################

# 基底作成

###################

if (sd != 0) set.seed(sd)

## 必要基底数コッダ: 取

if (nb == 0) bb_n <- trunc(exp(2.1328+0.8023*inp_d) / inp_d)

else bb_n <- nb

rn <- bb_n * inp_d ^2 # 必要 一様乱数 数

basis <- array(runif(rn), c(inp_d, inp_d, bb_n))

# 直交化

basis <- apply(basis, 3, gso)

basis <- array(basis, c(inp_d, inp_d, bb_n))

###################

# 取 射影 残差計算

###################

prj <- array(0, c(inp_n, inp_d, bb_n)) # 射影用

res <- array(0, c(inp_n, inp_d, bb_n)) # 残差 取

wt <- array(0, c(inp_n, inp_d, bb_n)) # ゞ゠゜ダ

bwt <- rep(0, inp_n) # タヴシ 最良基底 よるゞ゠゜ダ

kijun <- qchisq(0.95, inp_d)

Fprj <- function(pj) t(pj %*% t(inp)) # 射影ベェダャ 大 計算

prj <- apply(basis, 3, Fprj)

prj <- array(prj, c(inp_n, inp_d, bb_n)) # 整形

medi <- apply(prj, c(2, 3), median) # 中 数

madx <- apply(prj, c(2, 3), mad) # 中央絶対偏差 / 0.674 (標準偏差化)

for (i in 1:bb_n) { # 基底数 ャヴプ

res[,,i] <- t(abs(t(prj[,,i]) - medi[,i]) / madx[,i]) }

### ゞ゠゜ダ刈り込

if (tm == "CAN") {

k0 取 <- which(res <= 1.75)

k1 取 <- which(res > 1.75 & res <= 3.5) k2 <- which(res > 3.5)

wt[k0] <- 1

wt[k1] <- 1.75 / res[k1]

wt[k2] <- 0

}

else { 取 取 取 取取 取 取 取 # Huber-like 刈り込

k0 <- which(res <= sqrt(kijun))

k1 <- which(res > sqrt(kijun))

wt[k0] <- 1

wt[k1] <- kijun / (res[k1]^2) }

wts <- apply(wt, c(1,3), prod) # ゞ゠゜ダ 積和

bwt <- apply(wts, 1, min) # 最良基底を選択

### 取 最初 ュトケダ 共分散行列

u1 <- apply(inp * bwt, 2, sum) / sum(bwt)

V1 <- t(t(t(inp) - u1) * bwt) %*% (t(t(inp) - u1) * bwt) / sum(bwt^2)

### V1 ゠メヴ処理

### sum(bwt) ゴュ u1 V1 NaN る ゴュ 置換 異常終了を回避 る

u1 <- ifelse(is.nan(u1), 0, u1) V1 <- ifelse(is.nan(V1), 0, V1)

### 取 ュトケダ 主成分算出取取 取

eg <- eigen(V1, symmetric=TRUE) 取 取 取 取 # LAPACK使用取

ctb <- eg$value / sum(eg$value) # 寄 率

###################

# 回目 射影 最終ゞ゠゜ダ決定 ###################

res2 <- array(0, c(inp_n, inp_d)) # 残差

wt2 <- array(0, c(inp_n, inp_d)) # ゞ゠゜ダ 元

wts2 <- array(0, inp_n) # 最終ゞ゠゜ダ取 積和

prj2 <- t(eg$vector %*% (t(inp) - u1)) # 射影ベェダャ 大

medi2 <- apply(prj2, 2, median) # 中 数

res2 <- t(abs(t(prj2) - medi2) / madx2) # 残差計算 ### 残差刈り込

if (tm == "CAN") {

k0 <- which(res2 <= 1.75)

k1 <- which(res2 > 1.75 & res2 <= 3.5) k2 <- which(res2 > 3.5)

wt2[k0] <- 1

wt2[k1] <- 1.75 / res2[k1] wt2[k2] <- 0

}

else { 取 取取 取 取 取 取 # Huber-like 刈り込

k0 <- which(res2 <= sqrt(kijun))

k1 <- which(res2 > sqrt(kijun))

wt2[k0] <- 1

wt2[k1] <- kijun / (res2[k1]^2) }

wts2 <- apply(wt2, 1, prod) # 元 積和

if (tm == "EUR") wts2 <- pmin(wts2, bwt)

# EUREDIT版 一 ゞ゠゜ダ 比較 い方を 用

# ィヂジ版 ゞ゠゜ダを 使用 ###################

# 取 最終 置ベェダャ 共分散行列 ###################

# 置ベェダャ

u2 <- apply(inp * wts2, 2, sum) / sum(wts2)

V2 <- t(t(t(inp) - u2) * wts2) %*% (t(t(inp) - u2) * wts2) / sum(wts2^2)

return(list(u1=u1, V1=V1, bwt=bwt, u2=u2, V2=V2, wts2=wts2, eg=eg, ctb=ctb)) }

###################################################################

# gso: 基底を直交化 る関数 取 取

###################################################################

# Gram-Schmidt Orthonormalization取 関数msd 使用

# 正方行列を り 横ベェダャ同士を直交化 戻

###################################################################

gso <- function(basis) {

bd <- ncol(basis) # 横

bn <- nrow(basis)取 # 縦

basis[1,] <- basis[1,] / sqrt(t(basis[1,]) %*% basis[1,])

for (i in 2 : bd ) {

wk1 <- basis[i,]

for (j in 1:(i-1)) {

wk2 <- basis[j,]

basis[i,] <- basis[i,] - (t(wk1) %*% wk2) * wk2

}

basis[i,] <- basis[i,] / sqrt(t(basis[i,]) %*% basis[i,])

}

return(basis)

################################################################### # 取取 取 取 取 取 取MSD法多変量外れ値検出関数 使用例

###################################################################

#source("MSD.r") # 関数類を ネ゙゜ャMSD.r 収 場 使用

# 山火 タヴシ呼 出

data(bushfire, package="robustbase")

dat <- as.matrix(bushfire) # タヴシを行列化

n <- nrow(dat) # タヴシ数

d <- ncol(dat) # 変数 数

# MSD法

msdout <- msd(dat) # EUREDIT版 設定 る

# 算出 れ 最終 均値ベェダャ 共分散行列 ら 各タヴシ 中心 ら ブデメテニケ 方距 を算出

mah取 <- mahalanobis(dat, msdout$u2,取 msdout$V2)

# 検定統計量を計算

FF <- mah * ( n - d )* n /(( n^2 - 1 )* d)

# 外れ値 基準 Ｆ分布

cf99 <- qf(0.99, d, n - d)

cf999 <- qf(0.999, d, n - d) # 目安 る基準値

# 外れ値ネメエ取 取 正常値 1 ot <- rep(1, n)

# 基準より大 い ネメエを2 コッダ

ot[which(FF > cf999)] <- 2 # 外れ値

# 外れ値 数 タヴシ番号を表示 length(which(ot==2)) which(ot==2)

# 外れ値を色分 散布 行列 プュッダ

取 pairs(dat, pch=19, col=ot)

# Q-Qプュッダ

qqplot(qchisq(ppoints(n), df=d), mah, pch=19, col=sort(ot), main = "Q-Qプュッダ",

xlab="ィ゜ 分布 よる理論値", ylab="ュトケダ推計 ブデメテニケ 方距 ")

紙 取 クプポヤヴクミンタヴシ 設計取 取

○取 正規分布

取 正常値 分布 均0 標準偏差1 正規分布

取 タヴシ数 100

取 変数 数 5, 10, 20

取 変数間 相関 0, 0.4, 0.8

取 外れ値 分布 正規分布

取 外れ値割 0%, 10%, 20%, 30%, 40%, 50% 取 外れ値 原点 ら 距 5, 10, 100 取 第1軸方向

取 外れ値 標準偏差 0.1, 1, 5 ○取Skew-T分布

取 分布 種類 均0 標準偏差1 正規分布

取 タヴシ数 100

取 変数 数 5, 10, 20

取 変数間 相関 0, 0.4, 0.8

取 歪 わい , skewness 0, 1, 5, 10 取 第1軸方向

取 自 1, 10, Inf 無限大

取 外れ値 分布 正規分布

取 外れ値割 0%, 10%, 20%, 30%, 40%, 50% 取 外れ値 原点 ら 距 10, 100 取 第1軸方向

取 外れ値 標準偏差 0.1, 1, 5 ○取 複 フワサン分布

取 分布 種類 複 フワサン分布 ドメベヴシ p, mu, ph

p: power, 2: Gamma, 3: Inverse-Gaussian 2.5

mu: mean 1

ph: dispersion 1

取 取取 ※取 各変数 単変量複 フワサン分布 従う乱数を発生 いる カヤケキヴ分解 よ 相関 入 いる 最終的 作成 る多変量タヴシ 厳密 複 フワサン分布 いえ い

取 タヴシ数 100

取 変数 数 5, 10, 20

取 変数間 相関 0, 0.4, 0.8

取 外れ値 分布 正規分布

取 外れ値割 0%, 10%, 20%, 30%, 40%, 50% 取 外れ値 原点 ら 距 10, 100 取 第1軸方向

取 外れ値 標準偏差 0.1, 1, 5 ○取 対数正規分布

取 正常値 分布 均0 標準偏差1 相関付 正規分布を指数化

取 タヴシ数 100

取 変数 数 5, 10, 20

取 変数間 相関 0, 0.4, 0.8

取 外れ値 分布 正規分布 正 数 るよう絶対値化

取 外れ値割 0%, 10%, 20%, 30%, 40%, 50% 取 外れ値 原点 ら 距 10, 100 取 第1軸方向

紙 取 使用 ゾケダタヴシ一覧取

取

取

Hawkins-Bradu-Kassタヴシ取

変数 応答変数 ウイ タヴシ 外れ値 干ィ No.干～干ィ 取 干緑ェィ Hawkinsら 作成 人工タヴシコッダ

出典緒取Hawkins, D. M., D. Bradu, and G. V. Kass 干緑ェィ , Location of several outliers in multiple

regression data using elemental sets, Technometrics, Vol.26, pp.197-208

取

ケ゜ケ ヤケダメン業タヴシ取

変数 従業者数［対数］ 売 高［対数］ 干平ウ年 タヴシ 取

干緑緑イ ケ゜ケ企業コンキケ ヤケダメン業 擬似タヴシ タヴシ自体 公開 れ い い

プュッダ 点 置情報 ら擬似タヴシを作成 取

出典緒取Béguin, C. and B. Hulliger 平00年 , Robust multivariate outlier detection and imputation with

incomplete survey data, EUREDIT Deliverable D4/5.2.1/2 Part C

Hertzsprung-Russellタヴシ取

変数 星 表面温 対数 密 対数 ィウ タヴシ 取

出典緒取Rousseeuw, P. J. and A. M. Leroy 干緑ェウ , Robust Regression and Outlier Detection, John Wiley

& Sons

取

Bushfire 山火 タヴシ取

変数 年ェ タヴシ 取

山火 痕跡を分析 る 衛星 ら測定 タヴシ取

出典緒取Campbell, N. A. 干緑ェ緑 , Bushfire mapping using noaa avhrr data, Technical report, CSIRO

Stacklossタヴシ取

変数 平干 タヴシ 外れ値 No.干ん取平ん取年ん取ィん取平干

゚ンペッ゚を酸化 硝酸を作る工場 平平 日分 吸収塔損失タヴシ 生産 れ 硝酸 向流

吸収塔 吸収 れる 変数 れ れ操業率 冷却水 温 酸 集中 ゚ンペッ゚損失量 取

出典緒取Rousseeuw, P. J. and A. M. Leroy 干緑ェウ , Robust Regression and Outlier Detection, John Wiley

& Sons

取

Modified Wood Specific Gravityタヴシ

変数 応答変数 20タヴシ 人工タヴシ 外れ値 No.ィん取①ん取ェん取干緑

出典緒取Rousseeuw, P. J. and A. M. Leroy 干緑ェウ , Robust Regression and Outlier Detection, John Wiley

& Sons, P243

参考文献

[1] Béguin, C. and B. Hulliger 平00年 , Robust Multivariate Outlier Detection and Imputation with Incomplete

Survey Data, EUREDIT Deliverable D4/5.2.1/2 Part C

[2] Campbell, N. A. 干緑ェ緑 , Bushfire mapping using noaa avhrr data, Technical report, CSIRO

[3] Donoho, D. L. 干緑ェ平 , Breakdown properties of multivariate location estimators, Ph.D. Qualifying paper,

Harvard University

[4] Franklin, S. and M. Brodeur 干緑緑ウ , A practical application of a robust multivariate outlier detection method,

Proceedings of the Survey Research Methods Section, American Statistical Association, pp.186-191

[5] Hawkins, D. M., D. Bradu, and G. V. Kass 干緑ェィ , Location of several outliers in multiple regression data using

elemental sets, Technometrics, Vol.26, pp.197-208

[6] Istat, CBS, SFSO, Eurostat 平00ウ , Recommended Practices for Editing and Imputation in Cross-Sectional

Business Surveys, EDIMBUS Project

[7] Maronna, R. A., and V. J. Yohai 干緑緑イ , The behavior of the Stahel-Donoho robust multivariate estimator, Journal

of the American Statistical Association, Vol.90, No.429, pp.330-341

[8] Patak, Z. 干緑緑0 , Robust principal component analysis via projection pursuit, M. Sc. Thesis, University of British

Columbia, Canada

[9] Peña, D. and F. J. Prieto 平00干 , Multivariate outlier detection and robust covariance matrix estimation,

Technometrics, Vol.43, pp.286-300

[10] Rousseeuw, P. J. and A. M. Leroy 干緑ェウ , Robust Regression and Outlier Detection, John Wiley & Sons

[11] Stahel, W. A. 干緑ェ干 , Breakdown of covariance estimators, Research Report 31, Fachgruppe für Statistik, E.T.H.

Zürich

[12] 岡曓政人 平00ィ 多変量外れ値検出法 研究動向 表技術研究ヤフヴダ干 独 統計コンシヴ研

究コンシヴ pp.干-年ィ取

[13] 林良行 平00緑 ムヴュッド るタヴシ゠タ゛ゾ゛ンエ及 補定 関 る調査報告～EDIMBUS

プュグゟェダを中心 ～ 統計研究彙報第 ①① 号 総務省統計研修所 pp.干0干-干平緑取

[14] 澤取 正 干緑緑平 統計処理 岩波書店 pp.干干取