地盤・建屋相互作用系の時刻歴解析と周波数解析の等価性に関する基礎的研究

【論　 文】

UDG ：624

．

042

．

7 ；550

．

34

．

09

　 　 日本建築学会構造系論文報告集 第418 号

・

1990尓12 月

Juurnul　of　Struat

、

　Constr

、

　Engng

，

　AIJ

，

　No

．

418

，

　Deu

．

、

19YO

地 盤

・

建

屋

相 互 作 用 系

の

時 刻歴 解析

と

周 波 数 解 析

の

　　　　　　　　　等価性

に

_関

す る

基 礎 的研 究

STUDY

　

ON

　

THE

　

TIME

−

DOMAIN

　

RESPONSE

　

ANALYS

工

S

　

METHODS

CONSIDERING

　

SOIL

−

STRUCTURE

　

INTERACTION

　

EFFECTS

　

IN

　　

COMPARISON

　

WITH

　

FRE

_Ω

UENCY

・

DOMAIN

　

METHODS

　　　　 林

康 裕

＊

_{，勝 倉}

_裕

＊ ＊

Yasuhiro

　

HA

　

YASUI

　_and 　

Uiroshi

　

KA

　

TUKURA

　

We

　present　various 　types　of　evaluation 　methods 　_of　causal 　

discre

_七eimpulseresp 〔mse 　of　unbound

．

ed　soil

_，

　which 　are　necessary 　

for

　the　substructure 　approaches 　working 　in　the　time

−domain

　nonlinear response 　analysis 　considerlng 　the　soil

−

structure 　

interaction

　effects

、

　

The

　

discrete

　

impulse

　re

．

sponses 　are　obtained 　either 　

by

　the　Hiibert　transform 　usillg　the　FFT 　algorithm _（Causal　FFT

treatment ＞of　the　

flexibility

　of　soil　calculated 　

in

　the　

bandlimited

　

frequency

　range 　or　

by

　the　

discre

．

tisation　of　the　continuous 　impulse　response 　

formulated

　in　the　lime　

domain．

　The　

dynamic

　_prQperty

of　the　

impulse

　responses 　and 　their　effects 　to　the　response 　analyses 　are　examined 　

by

　comparing 　the

asympt 〔｝tic　property　of　the　

flexibility

　soil　in　the　

frequency

　with 　the　asymptotic 　properヒy ‘）f　the　

im．

pulse　response 　in　the　time　

domain，

　and　through 　earthquake 　response 　analyses

，

　

KegwerdS

：soil

−

structure 　

interaction

，

厂esPonse 　analcrsis　method

，

　time

・

domain，

　

freeuencydOmain

，

　

llil

・

　 　 　 be厂ごtransform

，

　FFT

1．

序 　近 年 まで

，

建 屋

・

地 盤 系の応 答 解 析 を行う場 合

，

周 波 数 領 域で_解析 を行うこ と が

一

般 的で あっ た

。

こ れ は

，

地 盤の特 性が周 波数 依 存 性 を有してい る の で， 解 析 結果の 考 察が周 波 数 領 域の方が容 易であり

，

数 値 解 析 上の定 式 化 も周 波 数 領 域の方が容 易である た め と考え ら れ る

。

し か し

，

建 屋 や建 屋 近 傍の地 盤の非 線 形 性 を 考慮 し た応 答 解 析につ い ては時 間 領 域で行 う方が容 易であり

，

時 刻 歴 応 答 解 析の重 要 性を無 視する ことは で き な い

。

　 本 来

，

周 波 数 領 域の_{情 報 と時 間 領 域}の情 報は フ

ー

リエ 変換を介して理 論 的に等 価で あり

，

時 間 領 域で得ら れ た 過 渡 応答 解 析 結 果1］

，

また は

，

過渡応答 実 験 結 果21か ら 周波数領域の_情報を導き だ すこ と が可 能で あ る と同 時 に

_，

無 限 振 動 数ま で考慮す れば周波 数解析で_得ら れ た地 盤の周波数応 答関 数 を も とに_， それ を 用い た 地 盤

・

建 屋 連 成 系の周 波 数 解 析と等 価な解 析を， 時間 領域で行うこ と がで き る3 ）

−

r

，

） 。 し か し

，

周 波 数 領 域で応 答 解 析 を行う 場合

，

建屋

・

地 盤 連 成系の_卓越振 動 数が 地震 波と同程 度 に低 振 勤 数領域に 帯域 制 限 さ れてい ること か ら

，

地 震 波 の時 間 刻み に対 応す るナ イキス ト振 動 数 以下の振 動数 範 囲で解 析が行わ れ ること が多い

。

こ れ に対して

，

地 盤の 周波 数 応 答関数のよ うに周波 数 広 帯 域な関 数を

，

周 波 数 領 域で応 答 解 析 を行う際に用い ら れ る よ う なナ イ キス ト 振 動数で帯 域 制 限す る と

，

そ の フ

ー

リエ _{逆 変 換と して得} られる イン パ ル ス応答は時 間に関す る因果律を満足 し な い。 非 因 果なイン パ ル ス応 答は

，

外 乱が加わ る以前に応 答が生 じて いることを意 味し

，

時 刻 歴 応 答 解 析に用い る こ と がで き ない

。

さ ら に

，一

一

般 の時 刻 歴 応 答 解析 手法で は

，

運 動 方 程 式の時 間 積 分の精 度 を確 保す る た め に

，

線 形 解 析で も地 震 波 を より細かい時 問 刻み に_{補 間}し て解 析 を行う

、

　

一

方

，

地 震 波や建 屋

・

地 盤 系の応 答 波の よ う な周 波 数 帯 域 制 限 関 数の場 合に は

，

適 当な時 間 間 隔でサ ンプリン グし て もそ の スペ ク トル特 性は ほと ん ど変わ ら ないが

，

地 盤の_{周 波 数 応 答 関 数}は非 常に広 帯 域で， これ を 逆 フ

ー

リエ _{変 換} して得ら れ るインパ ル ス応 答の_{継 続 時 間}は 短 い

。

周 波 数 応 答関数の ス ペ ク ト ル特 性を ゆ がめな いた め に は_， 地震波に比べ _て は るかに_小さ な時 間 間 隔でサ ンプ リング する必 要 が ある

。

特に_， 加 振 点近傍の インパ ルス 応 答は

，

衝 撃 力が加わっ た瞬 間に応 答 を生じ る

。

し た がっ 本 論 文 中の Fig

．

4は

，

文 献1］1_{の Fig}

．

_7の 再掲載で あ る

．

＊ _{満 水建 設 （株}1_{大崎 研究室}

・

_工修 ＊ ＊ _{清 水 建 設 （株}

1

_{大 崎 研究室}

・

_二L_博

Ohsaki　Research　InstLtu［e

。

　Shimizu　Corporation

，

　M

．

Eng

．

Ohsaki　Rじsea 【ch　Institute

，

　Shimizu　Corporadon

，

　Dr

．

　Eng

．

て その _{変 化}は急 峻で あり

，

通常の 地 震 波に対し て行わ れ る よ う な時 間 刻み でサ ンプリングを す ることには疑 問が 残る。 　以上か ら

，

地盤

・

建屋相互 作 用系の時刻 歴解 析と 周 波 数 解 析の_関係を考え るうえで _， （

i

） 時 間領域の解 析と 周波 数 領 域の解 析に 必要な周 波 数 範 囲 （対 応す る時 間 刻み）の_{関 係}を明ら かにする こと と

，

（ii） 解 析 的に得られ る連 続 的なイン パ ル ス応 答の特 性 と時 刻 歴 応 答 解 析で用い る離 散 的なイン パ ル ス_{応 答}の特 性の差を把 握す ること

，

が重要と な る が

，

こ のよ う な観点か ら考察を行っ て い る 研 究は ない。 　本 論 文では

，

周 波 数 領 域で_帯域 制 限さ れ た シス テム_関 数より得ら れ るイン パ ル ス応 答の物理的 意 味と

，

そ れを 用いたサ ブス トラ ク チャ

ー

法による建屋

・

地 盤相互 作 用 系の時 刻歴地 震 応 答 解 析手法につ いて考察し て_， 時 間 領 域の _{定式 化}と 周波 数 領 域の定 式 化の 関 係 を 明らか にす る

。

そ して

，

時 刻 歴 応 答計算に必要と な る離 散 的なイン パル ス応 答の評 価 法につ い てtFig

．

2

に示す よ う に， 帯 域 制 限され た シ ス テ ム関 数か ら FFT を用い て定め る方 法 （

hc

［n］は除く） と

，

解 析 的に求め たイン パ ルス_{応 答} か ら評 価する方 法を提 案し

，

そ れ ら が時 間領 域と 周 波 数 領 域で持つ特 性 を考 察すると と もに

，

既往の 方 法 との _相 違につ いて言 及する

。

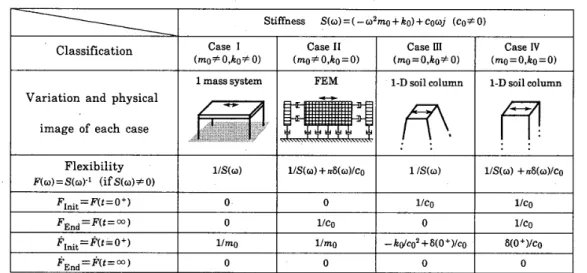
なお_， 本 論 文での_{考 察}は

，

特 性の 明 快さ と考 察の容 易さ か ら

，

Table　lの よ うに地 盤系を ユ自由 度 系に モ デ ル化 し て行っ て い る

。

また

，

本論 文で の議論は

，

建 屋

・

地 盤 連 成 系 を対 象に して行っ て い る が

，

一

_般の動 的サ ブス トラクチャ

ー

法に も適 用して 考え るこ と ができ る と考え てい る

。

r

「

叮

¶

一

r

ー

昏

｝

｝ 1

ー

幽

ー

ー

幽

1 − II

−

5

〜OII

−

StrUCtUre 　lntera 匸tlOn　SyStem

Strucしure 　 　 　 1

　　　　　

x ＿ ＿

潛

s 　 　 厂 　 　 ！

ノ

B：Artificial　Bound戲ry

「

1

ー

ー

ー

ー

II − IIII

ー

ー

1

ー

一

一

し

＿

一

一

一

＿

＿

一

＿

＿

＿

一

一

一

一

一

一

＿

＿

一

一

一

一

，

一

，

一

一

一

一

一

一

一

一

＿

鬩

P−一

一

一

一

一

一

一

一

一

一

一

一

凾

J

　

　

v

＋

▽

＼

丿

7

　　　

　　　　

　　　　

　　　

・

／

−

　 　 　 Input　mott 。n 　 　 　Flexibility　matrix 　 　 　 　［F（ω 】。 ・匚Fω】　 　 　 ｛嚇ω｝。r｛UG（t）｝ Fig

．

1　Schematic　view 　of　analysls 　and 　concept 　ofsubstructure 　 　 　rnethod

2．

解 析 対 象と解 析 手 法 2

．

1

　 動 的サ ブス トラ ク チャ

ー

法に よる時 刻 歴 応 答 解 析 　 　 と インパル ス応 答の評 価 　 解 析 対 象を

，

Fig

．

1に示す よ うな建屋

・

地 盤連 成 系と し

，

建屋およびその _{周 辺 地 盤}の _{非 線 形 性}ま た は不 均 質性 を考 慮し た時 刻 歴 応 答 解 析を行う問題 を考え る

。

解析に おい て は

，

建屋

・

地 盤 連 成系に仮想境 界を 設 けて

，

遠 方 地 盤と建 屋および周 辺 地 盤に分 離す る。 な お

，

遠方地盤 は線 形と仮 定す る

。

　建屋 とそ の周 辺 地 盤 を有限 要 素 等 に よっ て離散化 し た 場 合

，

その_第 n ス テップ （時刻

t＝

n△T ；△T は応答 計 算の時 問 刻み）に お け る絶対 変 位 系の釣 合い方程 式は 次 式で表 さ れ る

。

　

　

　

隠

：

ll

瀏

雛

1

・

［

ll

：

：

1

　

ll

：

：

1

］

繍

　

　

　

　

・

騾

1

鐸

：

1

鵬

ll

・ 、

晶ト

棚：

　 　　 　 　 　　 　 　

…・

…・

…………・

………

（1 ｝ こ こ で

，

_［M ］

，

_［C ］

，

_［K ］は

，

そ れ ぞ れ質量

，

減衰

，

剛性 行 列，

lu

（t）｝は応 答 変 位ベ ク トル で

，

添 字

B

は境 界上の 自 由 度

，

添 字

S

は その他の 自由 度を表す。

1P

（t）

1

は

，

建 屋お よ びそ の周辺 地 盤の非線形性を表す た めの外 力 項 で

，

線 形の _時には

io

｝で

，

非線形 化 し た 時に は 不 釣 合 力 （

；

（線形時の復 元 力 ）

一

（非 線 形 時の復 元 力 ｝）と な る。 また

，

IR

（t）

1

は仮 想 境 界に働く遠 方地 盤 との相

．

彑作 用力 で あ る

。

IR

（胡 をフ

ー

リエ _{変 換}した｝R（ω）

1

は

，

遠方地 盤 の境界に お け る柔 性 行 列 ［F（ω）］と

，

建 屋お よ び周 辺 地 盤 が ない時の応 答 変 位

IUc

（副 を用い て次の よ うに_表さ れ る

。

　 　　

lu

（tU）｝； ［

F

（ω）］

・

IR

（tO＞

1

・

・

………・

………・

……・

〔2） ただし

，

IU

_（tO）｝

・

＝

IUB

（ω｝｝

−

1U

　，，（ω）｝である。 　ま た

，

フ

ー

リエ _{変 換場} に お け る時 間 項を exp _けω の と す れ ば

，

（

2

）式の両辺の時 間 微 分に相 当する周 波 数 領 域の関係 式と して次式が得ら れ る。 た だ し

，

」

＝

（

−

1） v2 であ る

。

　 　　

j

・・

lu

（ω）

1

−

j

ω ［F（t・）］

’

IR

（ω〉レ

ー …一 …・

…

（3） （2）

，

（3 ）式よ明R（甜 が評 価で き れ ば

，

（

1

） 式 を解 くことによ り時 刻 歴の応 答 解 析を行うこ と ができ る

。

こ こ で

，

［F（ω）］お よ び ノω ［

F

＠ ）］の フ

ー

リエ 逆 変 換 は ［F（t）］お よ び ［

F

（

t

）］で

，

遠 方 地 盤の境 界を周 波 数 領 域 で単位 加振し た時の変 位ベ ク トル ま た は速 度ベ ク トル を

，

逆フ

ー

リエ _{変 換}し て得られるイン パ ル ス応答で構成 さ れ てい る

。

（2 ）式の逆フ

ー

リエ _{変 換}は次式で表 さ れ る

。

　　　

1

・（・）

1

−

f

：

［・（・）］

IR

（t

− ’

・）

ld

・

一 一 …・

…

〔4）

．

ヒ式は

_，

_［F（t）］と ｛R（酬の時 間囚果 性

，

す な わ ち

，

　　　

［F（t｝］

＝

［0］

，　IR

（t）｝＝ ｝0｝

　

（tく0｝

・

・

・

・

…

　

一…

　

（5 ） が 成 り立っ てい る の で

，

次の よ うに書き換え ら れ る。

　

　

　

・・ω・

イ

… r_・］・

1

・・

t−

r_）

1

…

’

・

・

…・

一 …・

・

・

・

…

　

書

碧

瓢

鱗

驚 認

灘謙

留 二

扇

こ こ で

，

_時刻歴 応 答解析を行う場合

，

解析結 果と し て求　　い

t

時間 刻み を △

t

（

＝

π／ω κ）とすれ ば

，

時 刻

t＝

め ら れ る

IR

（t）

i

の 時間 因 果性は常に満足 さ れ る

。

［

F

（t）ユ　 n△

t

で の値を意 味してい る。 離 散 イン パ ル ス応 答の時 の _{時 間 因 果 性}は_{， 時間 領域}で _［

F

_（t_）］を直接 定 式 化し た　 　問 刻み △ tは_， 応答計算の_{時 間 刻}み △

T

よりも大き く

，

場合に は自動 的に満足 さ れ る

。

し か し

，

周波 数 領域の定 　　 1以 上の整 数 m と， 式 化に よ り算 定され る _［

F

（ω）

1

は非 常に広 帯 域の関数で　 　 　 　 △ t

＝

m

・

△

T ………・

…・

・

…・

…・

…………・

・

《8） あ りt フ

ー

リエ 逆変換に よっ て ［F （

t

）］を求める場 合は

，

　 の 関係が ある と す る

。

上 式は_， 時刻歴応 答 計 算で必 要と 無 限振 動 数ま で［

F

（ω）］を 考 慮し た場 合に の み［

F

（t｝］の　 　な る振 動 数 範 囲が

，

地 盤 柔 性の周 波 数 依 存性を考慮す る 時 間 因 果性が満足 される

。

し か し

，

有限 要素 法や 境 界要

　　

振動数 範 囲の m 倍である こと を意 味す る

。

素法を用い て _［F（ω）］を 計算する場合に は_， 無限振 動数　 　 　

he

［n］

，

　

h

。［n］，　ht。．［n］は， シ ス テム 関数

H

（ω｝の 実 まで計 算する ことは不 可 能である し

，

さ らに_， メ ッシュ 　 　部だ け

，

虚 部だけ

，

および両 方 を

FFT

で逆 変 換し た も 分割 等の モ デ ル化上 の 制 約に よ り

，

高 振 動 数領 域の の であ る

。

し たがっ て

，

時 間に関し て he［n］は偶関 数

，

［F（ω）］の 精 度を保 証する こと がで き な い

。

有限の振 動　 　

he

［n］は奇 関 数であ る

。

数 範 囲で計 算 を打ち切っ た［F（ω｝］をフ

ー

リェ逆 変 換 し　 　 ま す， 周 波 数 領 域で定 式 化し た システム関

tw

　

H

（ω）か て近 似 的に求め ら れ る _［F（t）］は

，

非因 果 と なっ て し ま　 　ら求ま る 因果的な離散イン パ ル ス応 答につ い て説 明 す う

。

［F（t）］が因 果 的で な い場 合 （例え ば_， 後 述の

Fig．

4 　　る

。

（

b

）参 照 ）

，

ある時 刻

t＝t

。の応 答

iu

（酬 を 求め る た め　 　（の 　飯［n］と

h

，［n］ に は

t

＞

t

。の

IR

（朗 が必 要と な り， 逐 次 時 刻歴応答計算

　　　h

，［n］と

h

，［n］は

，

各々 he［n］

，

　 h

。

［n］の 因 果的な部 を行うこ と が で き な いe もし， ［F （t）］の非因果な部 分を　 　分 を2倍 して取り出 した もの であり

，

次 式で表さ れ る

。

無 視す る と

，

後 述の例 題で 示す よ うに_{低 振 動 領域}の

　　 　　 h

，［n］

＝

2U ［n］

・

he

［n］

…・

…’

…’

………

（9 ） ［F（ω）］が ひずん で し ま う

。

し た が っ て_， 有限の振 動_数

　　　　 ht

〔n］

＝

2　U ［n_］

・

h

。

_［n_］十h窄_δ＊ ［n］

……・

……

（10 ） 範 囲で定 義された地 盤柔 性を

，

そ の低 周 波 数領域の ひず

　　

ここ で

，

δ＊ ［

h

］

，U

［

h

］は次 式で定 義される

。

み を出 来る だ け小さ く抑え て

，

かつ

，

_インパル ス応答が

　　　　

δ＊ ［

k

］＝＝

1

_（

k＝0

_｝

，

0

　

_（

k

_≠0_）

………・

・

’

…’

”

_（U _） 時 間閃 果となる よ うに変換 す る

，

次節で示 すような方 法

　　　　　U

［

h

］

＝

0



（

k

＜0）

，

0

．

5



（

h＝

0）

，

1

　

（k＞O）

．

が不 可 欠とな る

。

　 　 　

・

……・

…・

…・

…・

…＿＿．

＿．

（12） 2

．

2



離 散 インパル ス応 答の_{評価 方}法



飯 ［n］は

H

（ω）の実 部 だけ か ら定 まり

，h，

［n］は

H

（ω｝の

　

シ ス テ ム関数

H

（ω）の入 力 を

x

（ω〉

，

出 力 を

y

（ω）と す

　　

虚 部だ けか ら定まる

。

_毎［n_］は_，

H

_（ω）の実部お よ び実 れ ば

，

（2｝， （3 ）式と 同形の次の関係が成り立つ ．　 　 　 部とヒ ル ベ ル ト変 換 対 61

・

η を 構 成す る虚 部か ら定ま るイ 　 　　

Y

（ω）

＝H

（ω）

・

X

（ω〉

……・

………・

…・

……・

…・

・

（

7

）　 　 ンパ ル ス応 答に相 当し

，hl

［n］は

，

　

H

_（ω）の虚 部お よび Fig

．

2 に

，

帯 域 制 限され た シス テム関 数　

H

_（ω）か ら因 果　 　虚 部とヒ ルベ ル ト変 換 対 を構 成する実 部か ら定まるイン 的で離 散 的なイン パ ル ス応 答を定める_幾つ か の_方法 を示

　　

パ ルス_{応 答}に相 当 する。 そ して

，

△

t→

0の場 合に は， す

。

図 中の FFT は

，

ナ イ キス ト振 動 数 をtON， フ

ー

リ　 　

h

（t）との間に

，

次の関 係か成 り立つ

。

　 　　 　 　 　　 　 　 　　 　 　　 　 　 　　 　 　　 　 　 　　 　 　　 　 　 　　 　 　

h

（n△

t

）

＝h

，［n］

；2

　

he

［n］（n≧

O

｝

．

＿

…駕

　 　

1”ve「seFF 「

　 　 　

跚

　 　 　 　

………・

・

…・

…

_{（13 ）}

1

一

盤

撥

一

鑠

钁

∵鬻 驚

1

；

；

臨

轟

騨

靆 肺 醸 醵

…

農 齢 島 野 灘 難 覊 Fig

．

2

韈

_{韓 難}

_聾

_灘

_羅

_∴

_；

1

　 　 　　 　 　　 　 　 　　 　 　　 　 　 　　 　 　　 　 　 　　 　 　　 　 　 　， 周波数領 域の実 部の平 均 　 　 　　 　 　　 　 　 　　

i

　 　 　 　

i

：

i

　 　 　

i

値に対 応 する n

・

＝

O で

h

，［

0

］

＝h

。［

O

］…

O

h

_．

，。］

igl

。m、。、　

i

と な り

・

… ［・・（・）］の低 振 轍 領 域の誤

　

　

　

　

　

　

躍

継

’

鋼

・

・

… ：

_…

聯

石ヂ

…

蕉

力

矯

畿

轟瓣 膿

岩

早

Evaluati。n 。f　causal 　discrete　impulse 　respQnse  る関 数 h＊_δ＊

［n］が周波 数 領 域で

一

定の_実

数 値に対 応する性 質を利用 して

，

平 均 値 0と して求まっ た実 部の値に対 し て

一

定 値 を 加え_， ω

＝

ω。近傍で誤 差 を小 さ く して いるこ とに相 当 する （後 述の

Fig．

6（

b

）t（c） 参 照 〉

。

（ii）　

hc

［n_］と

hCN

_［n_］ 　

hc

［n］は

，

次式の よ う に

，

実部

・

虚 部 両 方を用い て計 算 し た

hc

。

．

，

［n］の 因果的 な部 分を取り出 し た もの で あ る

。

　 　 　

hc

［n_］

＝

σ＊ ［n_］

・

hω．

_［n_］

一

凾

幽

・

・

…一 …………

（16） こ こ で

，U

＊［

ic

］は

，

次式で定義 さ れ る

。

　 　 　

U

＊ ［

k

］

＝

0 　（

h

＜0＞

，

　 1　（

h

≧

0

）

・

・

・

…

　

一・

・

・

・

…

　（17）

hc

［n］は

，

　Q）N を十 分大き く し て 逆変換し た場 合に （△

t

→ 0 ）_{時 間 因 果 的 と な り}

，

_{デ ジ タ}ル _{信 号}処 理の分 野で し ば し ば 用い ら れ る もの であ る。 　

hCM

［n_］は

hc

［n_］の

0

_秒の値を が に修 正 したもの で あ り

，

　　　hCN

［n_］

＝

（1

− U

＊ ［

−

n_］）

・

hc

［η］十

h

＊δ＊［n］

…

（18 ） で与え ら れ る

。0

秒の値

h

＊ _は

_，h

，［n］の場 合と同 様に

，

　　　Re ．

［

HCM

〔ω o）］

＝Re ．

［H（ω o）］

…・

……・

・

・

……’

（15）

’

を満足 す る よ うに_決め る。 ω。

＝

0の場 合

，

こ の 修 正は 妬

．

［n_］の_非因果な部 分の_特性を失わ ないように

，hc

_［n］ に対して

，h

、、．［n］の非 因 果な部 分の総 和を hc ［0 ］に加 え たこ と に相当 する。 そ して

，

後の例 題でも示す よ う に （

Fig．

4（

b

＞参 照）

，

イン パ ル ス応 答の非 因 果な部 分VS　

O

秒 近傍に集 中す ること か ら

，

直感的に も諾け る近似と なっ て い る。 な お

，hCN

［n］は

h

，［n］とh，［n］の平均値 と なっ て いる

。

（iii）　　　ん皿 ［n］ 　

一

方

，

△ t間 隔の離 散 イン パ ル ス応 答は

，

時 間領 域で 定式 化し たイン パ ル ス応 答

h

（t）か ら作ることもで きる

。

Fig

．

2の _{妬 ［}n_］は

，

△ t間 隔で

h

（

i

）の平 均 値を言

1

．

算 し た もの で

，

次 式で表され る。

　　　

h

・［n］

一

郡

：

野

・（曲

・

……・

…一 ・

……

_（19） 　 Fig

．

2に示し た5つ の離 散 イン パ ル ス応 答を総 称し て ん臥［n］と 呼 び

，

そ れ らを

FFT

で周波 数 領 域へ _{変 換し} て

一

tUN≦ω 〈 ω N の範囲 で 求ま る帯 域 制 限 シス テム

Hc

（ω），　

HCM

（ω），　

HR

（a）），　

H

，〔ω）お よ び

Hm

（ω〉を総 称 し て H：．

，

（ω）と呼ぶ

。

こ こ で 注 意を要すべ きこ とは

，

H（ω〉と

h

（t）を_{H 臥}（ω）や ん_鋲［n］に置 換 し た の で は な く

，

次 式 の よ う な

H

 （ω）の 周 期 化 関 数 H 翫（ω）と デル タ関 数 列 硯呈ω に 置換し たことで あ る

。

H 讖（ω）

＝

Σ 瑞 ．

：

（ω＋2iω．）

………・

・

…

（20） 　 　 　 　 ‘

＝

−

an

h

：：（t）

＝

Σ △ t

・

h：

，

，圃 δ（t

−

_{k△ 診）}

…・

・

…

_（21） 　 　 　 配

己

一

qt 2

．

3

　 相互作用 力の_{評 価} 　シ ステム に対する入力が帯 域 制限 関 数 （

X

（w）

＝

O（

1

ω

1

＞ WN ）） と み なせ

_，

　

I

　bl　

1

〈 a）N の範囲で

H

（ω）定

H

  _（ω〉な ら ば

，

次 式が成り立つ _。 　 　 　

y

（ω）

− H

（ω｝

・

X

（ω）＝

H

 _（ω）

・

X

（ω）

　　　　　

＝

HX ζ

_（・・）

・

x

（ω）

…・

・

…・

：

t……・

…一 …・

（22） （22 ）式をフ

ー

リエ 逆変換して _（21_）式を代入 し

，

嬬

，

N ［n］の因果性の条件を考慮し

，IAt

を イン パ ル ス応答の 継続時間 （ん  ［

k

］＝

OU

_〈

h

≦

N

／

2

））と す れ ば

，

　 　 　 l

　　　

y ［n_］

；

_Σ△ t

・

x _［n

−

hm ］h：

．

，

［

h

］

・

……・

・

…

〔23） 　 　 　 尾

一

〇 の 関 係が得ら れ る

。

ただし

，

イン パ ル ス応 答 硝．［n］の 時 間 刻み は前 述の _{よ う}に

．

△ tで あ る が

，

その_他の_{時 系} 列 関 数の時 間 刻み は △

T

（△

t＝

m △

T

）で あ る

。

例え ば， X ［n］は t

＝

n△ T での値を 表 してい る

。

（23 ）式 を （2）式に適 用 し

，

iR

［n］｝につ い_て整理 す る と次 式が 得ら れ る

。

　　

　

IR

［n］

μ

盤 亨

1

　　

　　　　

（

lu

［n］｝

一

船 丁

自

［

F 剛

IR

［n

−

mi ユ

1

）

　　　　　　　　　

・

…

　

∵

・

・

・

・

・

・

・

・

…

　

7r・

r…

　

r・

・

・

・

・

・

・

・

…

　

（Z4） 通 常の時 間 領 域の定 式 化S）

・

9）_{で は}

_，

_{まず変位 イン パ ル ス} 応 答 ［F（

t

）］を 直接 計 算 し

，

’

（61 式を時 刻 歴 応 答 解 析の 時 間 刻み △

T

間 隔で離 散 化す ること に よ り

，

（

24

）式で m

＝

1とお い た場 合と同 型の 式を得る。 ま た

，Wolf

の 定 式 化勘 ま

，

周 波 数 領 域で定 式 化し た［

F

（ω）

1

を用い て ［F（t）］を計 算す る以 外は

，

基 本 的に時 問 領 域の_定式 化と 同じ である

。

す な わ ち

，

既往の定 式化は

，

（24 ）

．

式で m

＝

_{1と お}い た場 合に相 当し

，

時 刻 歴応答 解析の_{時 間刻}み △

T

を小さ く す る と， 非 常に

．

_{高い振 動 数の ［}

_F

_（ ω）］を 用 い て時 刻 歴 応 答 計 算 をして い る こ とに なる

。

これ に対し て_， （24 ）式の定 式 化は_， 離 散 イン パ ル ス応 答の 時 間 刻 み △

t

を 時 刻 歴 応 答 解 析の 時 間 刻み △T に比べ て m 倍にする ことがで きる の で

，

時 刻 歴 応 答 解 析で必 要と な る _［F（ω）］の振 動 数 範 囲を

，

m 分の 1に抑える こ と がで きる

。

　

一

方

，

（24｝式の誘 導と同 様に

，

（23 ＞式を （3 ）式に 適 用す れば次 式を得る。

lk

［n_］ト［

罧 亨

1

　　　　　　（

la

［n］｝

−

m △ 丁

盞

［lf

・

［

i

］］

IR

［n

−

mi ］｝

）

　 　 　

・

・

・

・

・

・

…

　

7・

…

　

r・

・

・

…

　

一・

・

・

・

・

・

・

・

…

　

一

（25） な お_，

．

林ら の 定 式 化4 ）は

，

（25）式で m

＝

1と おい た場 合に相 当す る。 ま た

，

以 下で は

，

（24｝式を相互作 用 力 の変 位 定式 化

．

（25＞式を速 度 定 式 化と呼ぶ

。

　（24）

，

（25）式の ［F ［O　_］］　K

’

_［F _［0 ］］は

，

衝 撃力 が加わっ た 瞬 間の 応 答 に相 当 し

，

時 間 刻み △ tが十 分小さ け れ ば対 角マ ト リク ス とな るが

，

応答 解 析の_{時 間 刻}み △T

に対 し て十 分に大き く △ tを取る こ とに よ り対 角マ ト リク スとみ なせ な く な る。 この時

，

逆マ トリク スを 計 算 するた めに三角 分 解の必 要が生 ずる

。

ま た

，

（24＞式の ［

F

［o ］］

−

1／m △

T

は_， （1 ）式の右辺の _［κ副に足 しこ ま れ る付 加 剛 性 行 列 で あ る が， （25 ＞式 の ［

F

［

0

］］

一

’ ／m △T は

，

（1＞式の 左 辺の ［

CBB

］に足しこま れ る 付 加 減 衰 行 列と な る

。

そ し て_， 離 散 イン パ ル ス 応答 ［

F

［n_］］， ［

F

［n］］は， 小さ な n に対し て急 激な変化をす る ことが予 想され る か ら

，

［F ［0］」や［F ［0 ］］の精 度確 保 が_， 応 答 解 析の精 度の確 保上_， ひ い て は応 答計算の _{安 定} 性 を 保 証する上で重 要な意 味 を 持っ てい る とい え る

。

　

一

方

，

（24）

，

（25＞式 中の （　） 内 第Z項は

_，

過 去に 生 じ た相互作 用力に起因す る t

＝

n △ T に おける_仮想境 界の変 位 （速 度 ）を意 味して い る

。

こ の項は

，

イン パ ル ス応 答の継 続 時 間の間

，

m △

T

間 隔で

IR

［nl｝と ［

F

［n］］ の合 成 積の計 算を行っ て評 価する必 要が ある

。

し た がっ て_， 本 手 法は

，

応 答 計 算の時 間 刻み △

T

に比べ _て離散 インパル ス 応 答の 時 間 刻み △

t

が大きい 程 効率 的で

，

イン パ ル ス応 答の継 続 時 間が短く な るほど効 率 的で あ る

。

以 上か ら， イン パ ル ス応 答の

t＝o

近傍の特 性と継 続 時 間 特 性は

，

応 答計算 手 法の精 度 と 効率 性を議 論す る

．

ヒで重 要な意 味 を持つ こと が指摘でき るc

、

3，

イン パ ル ス応 答の構 造 と応 答 解 析 手 法 3

．

₁地 盤 柔 性の構 造と インパ ル ス応 答の_漸近特性 　本 節では_， 周 波 数 領 域での地 盤 柔性の_{特 性}と

，

Fig

．

2 の フ ロ

ー

に従っ て得ら れ る離 散 インパ ルス応答の特性を 対応づ けて_{， 体系的}な考 察を行う、 考察は

，

簡 単 さのた め に， 地 盤系を

Table

　

1

に示す よ う な

1

自 由度 系に モデ ル化して行う

。

　周波 数 領域の動的剛性

S

（ω）は次 式の_{運 動 方}程_式 　 　 　moU _〔

t

_）十Co血（

t

）十

h

。u（

t

＞

；

δ（

t

）

・

・

・

・

・

・

・

・

・

・

・

・

・

…

　〔26） を解い て

，S

（ω）＝ （

−

_{toemo 十}

j

ωCo十

k

。）と なる

。

ただし

，

δ（t）は

Dirac

の デル タ関 数で

，

対 象と して い る地 盤 系は_， 逸散 減 衰 特 性を有してい る と仮定 して c。≠0と する

。

動 的 柔 性

F

（ω）は

S

（ω）の_{逆 数}で あ る。

F

（ω）の ω

→

。。 に おける漸 近特性は

，Table

　

1

_{に示し たよ う}に

，

遠 方 地 盤 の解 析 手 法やモ デル化に よっ て次の よ うな差異が あ る

。

す なわ ち， 質 点 系や FEM 等の離 散 系の方 法に よっ て 求ま る動 的 柔 性F （ω）は

，

m 、≠0の場 合に相 当し， ω の 増 加に伴っ て

Case

　

I

，

　

fi

の よ うに ω

’

2の オ

ー

ダ

ー

で減 衰して い く

。

また， 境 界 要 素 法 等の よ うに連続 体系の手 法で得られる F（ω ｝は m 。

＝

Oの場 合に相 当し

，

ω → ・ ・ に お け る漸 近 特 性は

Case一

皿，　

IV

の よ うに な り，　

F

（ω） は ω

一

’のオ

ー

ダ

ー

で減 衰して い くと言わ れ ている10｝

。一

方

，

臨

＝

0と な る例と して は

，

遠 方 地 盤 を有 限要素等で モ デル化し

，

そ の 逸 散 減 衰を表 現する_{境 界 処}理 と して ダッ シュ ポッ トを用い る場 合な どに生ずる。 こ の よ う な 地 盤 柔 性 F（ω）の漸 近 特 性の差 異は

，

理論的なイン パ ル ス応 答の初 期 値 と最 終 値に以 下の よ うな影 響を及ぼ す。

　

ま ず，

F

（

t

）の初 期 値

Fi

。itは

，

ラプラス変換の初期値 定理か ら次式で表され る

。

　　　F

，

．

、，

＝1im

　

F

（

t

）

・

・

1im

　

lf

ωF（ω）ト

1

 

IF

（ω）

i

　 　 　 t

−・

o＋　　　　　　　　　

4co

　　　　　　　ゆ

り

on 　 　 　 　　 　 　　 　

・

・

・

・

・

・

・

・

・

・

…

　

一・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

…

　

’

（

27

） す な わ ち

，Finit

は

F

（ω｝の ω → OQ に お け る挙 動に よっ て支 配さ れ てい る。 そ して， m 。

＝0

の場 合に は

F1

．itは 1／Coに な る が

，

　 Mo ≠0の 場 合に は

Finit

＝

Oと な る

。

　

F

（

t

）の初 期 値

Finit

につ い て も 同様に

_，

　m

，

≠

0

の 場合は

1

／m 。で有限値で あ る が， 肌。

＝0

の場合に は

F

（ω）が ω → ・・ _で

一

定値 1／c 。に収 束す る か ら

，

時間領 域で δ（

t

） の 構 造の特異性 を 持つ

。

以 上の こと は

，

m

、

が 十 分 小 さ い場合の解析対 象振動 数 領域の システム関 数の特性は

，

m 。

；

Oの 場 合と ほ と ん ど同 じで あ る が

，

解 析結果に ほ と ん どの 影 響 を及ぼ さ ない 高 振 動 数領域で は両者の_{特 性} に 差 が生じ

，

イン パ ルス_応答の _初期値も異なっ て し ま う ことを意味して い る

。

　次に_，

F

（

t

）の最 終 値 FE

。

tiは

，

次 式の よ うに プωF（ω〉 の ω

＝0

に お ける値 と

一

致 する。

Table　lSnffness　and 　flexibility　coefficients 　of　one　degree　of　f［eedom 　system S雌ness 　S〔ω）

＝

（

−

02mo 輔 ol＋eo町

’

〔CO≠D） Classification 　　Case　I （mo ≠0

，

愚_o≠O_） 　　Case　i【 （mo ≠0

．

_陀0

＝

_ω 　　Case

　

Hl （尻0

＝

0

，

々0≠0_） 　　Case［V （肌0

＝

0

，

矗0

＝

D）

Variation　and 　_physical

　　image　of　each 　ease

1m躅 sysbem 　 　 　 　 ⇔ 　　偲轗鰯職懸

，

　

・

　 　

疲

醗 醐 羅蠱顧鞭

、

脚

．

滞

濁

．

簾 蟹 思 糖 笥 野

F

FEM

⇔

1

−

Dsoilcol  n

昂

，

　

　

　

　

　・

1

−

Dsoilcolumn

印

　■ 「

　昌 ・

　　　　Flexibility F（ω

＝

S仙）

．

L （if8〔ω）≠0_｝ 1虐 （ω） 1！S（ω）＋認 （ω）1Co 1〆S（ω 1／s（ω）＋πδ（ω）〆Co F 【

。

iL

二

列ε

＝

o

＋

｝ 0 0 1／CO 1／CO FE

_。

_d

＝

F〔ε

＝ワ

゜

） 0 11Co 0 1／CO 戸 正

。

iL

＝

恥

三

〇

＋

） 11  0 11瓰 

一

堀eo2 ＋ δ〔D＋_{yσo δ} 〔0＋_ycO 戸 躙

＝

即

二

。。1 0 0 0 0

一 101一

　 　　

FE

。α

＝hm

　

F

ω

＝lim

｛ゴω

F

（ω）ト

F

（ω

＝0

） 　 　 　 t

オ

co 　 　 　 w

イ

o 　 　　 　 　　 　 　 　

・

・

・

・

・

・

・

・

・

・

・

・

・

…

　

P・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

…

　（28＞ 解 析モ デル が静 的 剛 性 を持つ場合， すな わ ち，

h

。≠0の 場 合には

，FE

．d は

0

とな る が，　

k

。

＝0

の場合に は永久 変 位 1／c。 （≠O） を 生 ずる

。

また，

．

_FO

_{）の最 終 値}

_FE

。d に つ い て は_， c。≠0を仮 定し て い る の で， 必ず 減衰して 0 に収 束する

。

つ まり， 対 象と している系が減 衰を有す れ ば

，

インパ ル ス応 答は

t

→ ・D _で

一

_{定 値}に収 束す る

。

　以上 を ま と める と_， イン パ ル ス応 答の_{初 期値 （}

t

→

0

の 漸 近 特 性 ）は動 的 柔 性 F（ω）の ω

→

。 。 の漸 近 特 性に ， イン パ ル ス応 答の最 終 値 （t→ 。。の漸 近 特 性 ）は動 的 柔 性の ω→

0

の _{漸 近}特_性か ら定まる

。

この よ うに して_得られ たイン パ ル ス_応答の漸近特性を

Table

ユ に

．

整理 し て示す

。

3

．

2　離散イン パ ル ス応答の 特性

　

Table　lの地 盤 柔 性 を もとに

，

　Fig

．

2の フ_ワ

ー

に従っ て計 算し た

he

［nユと

h

。［n］の 時 間 因 果な部 分 （n≧O） の例 を， 解 析 解 h（t｝と比 較し て Fig

．

3に示す

。

　

FFT

で 用い た時間 刻み は

，

図中に示 し た無 次元化 時間 t’ に対 して 0

．

2

，

フ

ー

リエ 項 数 は128で あ る

。

ま た

，k

。

＝

0の 場 合に は

，F

（ω）は δ（ω〉の構造 を有し てい るの で

F

〔ω

；

_O）≡ 0 _{と お}い て_算定 して い る

。一

方

，h

（t）が δ（t）の 構 造 を 持っ Fig

．

3（

b

）の

Case一

砠

，

　

IV

の

h

（

O

＞は

，

便 宜 的に

h

（t）の

．

t

；0

近傍の平均 的な値と し て，　

h

（

0

）

＝

妬 ［ 0 ］と して図示し た

。

　〔9）

，

（10） 式 と Fig

、

3 か ら

，

離散インパ ル ス応 答の 形 状につ い て以 ドのこと が指 摘で き る

。

　 　 　

・

（ilh 。

；

0 の 場 合に は

，

イン パル ス 応 答

F

（

t

）は Fig

．

3

（a）の Case

−ll，

　

W

の よ うに永久変 位を生 ずる

。

he

［n_］は

，

　

F

〔ω

＝

q

）は

0

と おいて

．

求め たの で，　

he

［nl の平 均値 LS　Oとな る よ うに零軸が シフ ト して い る

。

一

方

，

he

［nj につ い ては零 軸は シフ ト しないが

，

直 線の トレ ン ドを持 ち 永 久 変 位が隼じ ない1％ （ii｝ Fig

．

3（

b

）の Case

−

M

，

　

W

の よ う に

，

　 h_〈t_）が δ（t） の構 造 を 持つ 場 合で も he［n］は t

＝

・

Oで 発 散せ ず

，

　

h

_， 0

，

3 　 D

．

20 ζ 囗

・

取

§

。

．

。

一

_〇

_．

1 L5 　 1

．

Os 』 0

，

58 　 0

．

口

一

〇

．

5 1

．

0 　 D

．

5s80

．

o

一

〇

．

5 1

．

5 　 1

．

0 ε 覧 o

・

5 り O

．

D

h

（n△t） he［n_］ o 2Case 　

I4

6

・

0 2Case 　

II4

6 0

一

_〇

_．

₅ 　 　 日 2Case 　

nI4

6 2Case 　

IV4

（a）　

lnpulse

　

displacement

　response 　 Fig

．

3 6 1

．

0 00

．

5

・

_ζ o 建0

．

0

一

_〇

_．

5 LO

So

・

5

’

％

建0

．

0

h

。［n］ 0

一

〇

．

5 　 　 0 　 5

．

0 　 4

．

D

（

3

．

D ご

’

_{k2 ．}

_Doe 　l

．

0 　 0

．

0 2Case 艮 4 6

一

t

．

0 　 　 0 　 5

．

0 　 4

．

OS3

・

o

’

_k2

_．

₀₈ 　 t

．

0 　 0

．

0 2Case 　

IIA

6

一

Lo 　 　 D 2Case 　llI4 6 2Case 　

IV4

（

b

〕　

Impulse

　velocity 　response Impulse　responses 　obtained 　from　the　 corresponding 　frequeRcy　functio皿s

［0］窟 _{編 ［}0_］とな っ て い る

。

つ まり

，

（9）_， （19）式より

，

h

，［0］は

t＝

O近 傍の平 均 的な値 を評 価して い るとい え

る

。

（iii） t＞

o

に おいて

h

。［nコと

h

。［n］に差が ある の は

，

t

＝0

近傍で不連続と な る

Fig．

3（a）の

Case一

皿 と

Fig．

3

（b）の

Case− 1 ，

　

H

の場合で あ り

，

そ の差は主と して t

＝

・

O近傍に集 中し てい る

。

t

＝

・

O近 傍の差は

，

（27）式か らも容 易に想 像で きるよ うに

，

ナ イ キス ト振 動 数 近 傍の 高周波 数 領 域の特 性の差に起 因し （後 述の Fig

．

6で は （a_）と （c｝の差に相 当す る ）

，

t

≡

O近 傍で急 激に変 化 す る加 振 点 近 傍の インパル ス応 答に特 徴 的に現れ る

。

　ま た

，

時 刻 歴 応 答 解 析 手 法の観 点か ら

，

（24） 式の変 位 定 式 化と （25＞式の速 度 定 式 化 を 比 較し て_{以 下}の点が 指摘で き る

。

（11 　

k。

＝

0

の場合

，

変 位 イン パ ル ス 応 答は永 久 変 位を 持つ か ら， t△ tが応 答 計 算の継 続 時 間と同じだ け必要 と な る

。

これに対して

，

速 度 イン パ ル ス応 答の継 続 時 間 は

_，k。

； 0の場合で も有 限で あ る

。

特に

，

地 盤の インパ ル ス 応 答の継 続 時 間は

，

地 震 波に比べ て は る か に短く_， ’△

t

を 必 要 以 上に大 きくする必 要 が ない ので

，

変 位 定 式 化に比べ て効 率 的で あ る

。

〔

ii

）

F

（ω）か ら

FFT

を 用い て算 定され る離 散 イン パ ル ス応 答に は

，F

（ω）を 算 定す る際の誤 差や

FFT

に ょ る変換時の誤差が含まれ る

。

m 。≠0の 場合に は

，

理 論 的な変位 イン パ ル ス応 答 F（t）は_， t

＝

0 で 0で_，　

t＝

O“ で急 激な増 加 を始める

。

し たがっ て

，

変 位 定 式 化 （（

24

｝ 式） 中の _［

F

［0］］は ［F ［

h

＞0］］に対 して小さ く

，

［

F

［

0

］］の_{相 対}的な誤 差を小さ く する こと が難し い

。

そ して_， ［

F

［0 ］］は_， その逆マ トリク スを計 算 し な ければ な ら な いの で

，

応 答 計 算を行う と発 散し て し ま うこ と も少な く ない

。一

方

，

速 度 インパル ス F（

t

）の場 合は

，

常に

t＝

0 近 傍で最 大値を と り

，

徐々 に減少して い くの で_， 速 度 定 式 化 （（

25

） 式）中の ［

F

［

0

］】は 比較 的精 度よ く求め る こ と が で き る

。

し たがっ て

，

速度 定式 化のほ う が応答 解 析の精 度と安 定 性に優れて いる といえ る。 3

．

3 　地 盤 剛性が

Case−

1

の場合 　Table　1の

Case− 1

の よ うに

，

地 盤の 動的_{剛 性}が静 的 0

．

5 0

．

4 　 o

．

ヨ 扈

腎

。

．

2 0

，

1 　 　 ん_尺圄 or 九〇岡

一一一

一

_hl ［司

一…齢

｝

_heM［n］ 　 　 　hm圄 0

．

0 　0

．

001　　　0

．

002　　　　　0

．

OO5　　　　0

，

0ユ　　　　0

．

02 　 　 　 △t（sec ） 　 　 　 （a ＞ cono ］

’

，

　

’

”

　

ノ

，

　

　

’

・

／ ／

　

7

！

！

　

・

’

！

　

　

！

ノ

　

　

、

〆

〆

　

　 　

r

！

／

　

　 　 ／ ン

　

　 　

　

彡

　

　 　

　

．

二

　

　 　

　

・

_・

_〆

ケ

　

　 　

　

　

彡

　

　 　

　

　

彡

　

　 　

　

　

　 多 51111

鹽

口

0

．

5 0

．

4

一

口

．

ヨ 9

’

覧

fiO，

2 0

．

1

丶、

、

_、

　

　

　

　 　

　

　

　

_、

°

w

蝿 　

　

　

　 　

　

　

　

・

、

丶

、

　

　

　

　 　

　

　

、

僕 　

　

　

　 　

　

丶

、

　

　

　

　 　 ＼ べ

、

　

　

　

　 　

丶

丶

　

　

　

　 ＼

、

＼ ＼

、

丶

＼

丶

　

　

、

　

、

丶

．

丶

、

　

、

丶

、

＼ ＼ 丶

丶

、

　 　 0

．

0 　 　 　 0

．

001　 　0

．

OO2　 　 　 　0

，

005　 　 0

．

Ol　 　 　O

．

02 　 　 　 △t（sec ） 　　 　　　 　　　 　（b）　moi 「［0ユ

Fig

．

5　1nitia且values 　of　causal　discrete　impulse　responses

1

．

000

．

？5

ハ

ロ

　

ss

髯

量

o

・

25 　 0

．

00 　 　 　

ロ

DCゆ　 　 　　　

ロ

　　　　 　　 　ロ

　

o　o　 　 　 　ロ

　

o6ロ　 　　 　o

　

　　ロ　　 　 　　

　

1oo 　

−

o

，

25L

＿＿＿＿

」

＿＿＿＿

一

＿

＿

J 2（sec ｝

冖

三 馬 o 建 1 　

…．

…・

一

　 △ £

；

0

，

010seo 　 　 　L口D 　 　 　O

．

751 　 　 　0

．

50 　 　 　0

．

〜5 　 　 　 　

7■

r

△ε＝0

．

001sec i

7「

「

噛

「

」

_ε（sec ） 』40 　 　

−

0

．

020　 　 　0

．

　

　

　「

■

．

0　 　　

，

n 囗 0

．

040　　　　　　0

．

660　　　　　　0

．

0臼囗0

．

L 1

．

OO0

，

75 （a） h〔t） 1

．

00D

．

75 h（t） 一

．

a

．

25」

＿＿

＿＿

L

＿＿＿＿

」

＿一

一

」

一一一一

」

一

一

一一

」 　hR［n ］ 1

．

00 （b）_htON［n］ 0

．

75

・

一

一

一一

ん_f圄 （h

＊

＝ 0_）

，

一

一

一

一

一

・

 九

肌

［π］ 　 　 　 1

．

00a

．

75 　 D

，

5D　 　　　 O

．

50　 　　囗

．

_{50　 　　　 D}

．

50

E

’

覧 0

、

25 　 　 0

．

25 　 　 D

．

25  0

．

25 建 　 0

，

00　 　 　 　0

．

DO　 　 　O

．

00　 　 　 　0

．

DO 　

−

。

，

25L

＿＿＿

」

＿＿ ＿

＿

」

一

。

．

25L

＿ ＿＿

⊥

＿

一

．

D

．

asL

− 一 一

⊥

一一一

」

．

囗

．

25L

−

一 L

− 一一

」

　 　 　 （c）　Causal　discrete　impulse　responses

　 　 　 　Fig

．

4　Discrete　impulse　responses

丿ωF（“）CO1

．

20

．

8D

．

40

．

O 　 o ：D

．

4

一

〇

．

8 Real

一

■

　

、

ミ

1

…　畠

二

25Hz53

，

驢

3

、

＆

＝

50Hz _な

＝

100H

・

r

o　 　 　 　

・

．

．

・

‘

6b

．

o

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

「

．

」

．

　

　

　

　

　

　

　

　

　

　

　

　

−馳

．

−．

！

寸 　　

，

．

／ _且00

．

_{D　 ら}

＝

250H露

．

．

「

「

」

　 　 　 　

．

・

−r「

．

’

幽

＝ 　 　 　 　

L．

≡ 　　　 　150

　

　

　

　

「

．

■

．

．

．

「

_・

_1．

．

．

・

．

．

．

　L國

L．

．

．．

．

．

r・

−「

．

L

・「

一

　　　　　　　　  ag

，

畠

＝

500Hz

．

ノωF（ω）CD12o

，

B FRE口UENCY　〔HZ】 （a）　HR（ω） 　

ロ

　 。

．

。 　 0

．

−

0

．

4　

一

〇

、

8 jmF（tU）Co 且

．

20

．

B0

，

40

．

0

一

〇

．

4

一

_〇

_．

₈ FREOUENCY 　［HZ〕 （b｝　Hr〔co）〔h

＊

＝O）

．

0 忌

、

　 丶 　Real

、

_＼





_丶

　丶　 　

丶

、

　丶

　

　

丶

　 　 　 丶

丶

　

、

　

　

、

　

　

　

、

樋 H

・

_刄

　

　

　

　

　

　

　

　

　

L 　　　　　

、

丶

る

＝

50H乙

、

、

一

　

一

　

一

一

 

＝

250Hz る

＝

500H

己

　

_一

　



　

_噌

　

_、

　



　



　

．

　

　

　

　

　

　

一

』 ・

ギ

・

・

　

辰 　　　＼且OlOOH2 ＼ 0 L50

　

一

Lnag

．

_ミ 　 FRE口UEN匚Y　［目Z］ 　 〔c）　 H，〔ω） 蜘

尸

び 2

．

Jl0

．

8o

．

40

．

D

一

〇

．

4

一

〇

．

8

、

Rea1 ＆

＝

25H

・

丶

_丶

　、

．

．

．

．

一

．

一

プ

1

な

＝

50H

【

冷

、

．

》＼

＝

10Q虚丶 　 　 　 丶 「

『

．

oL 

」

，

馳

_互

_．

　　　　

 

二

−’

．

0

．

1

_．

_．

　

　

　

　

　

　

　

　

　

　

　

　

一

「

．

0 畠

ヨ

250H・ 且50

　

　

　

　

　

　

　

　

　

　

　

．

．

「

．

　 　 　　 　

”

．

．

一

： Lnag

，

．

．

：

「

．

．

．

：

．

．

．

幽

．

「

．

． 一

．

．

｝

，

．

．

一

．

．

　　　　　　砧 500Hz jωKan）co120

．

60

，

4D

．

o

一

〇

．

4

一

〇

．

8 FRE囗凵ENCY　〔HZ］ 〔の　Hc〔ω）

　

_、



_丶

_Real

丶

一

畠

＝

25H乙

丶

_丶

　＼ 丶

　

_、



、

_、

　

　

　、

，

ノ

、 な

＝

50H

男

　

　

、

へ

≡

lo °H恥

・

丶

丶

丶

_丶

　

　

　

　

　一

一

一

．

．

一馳

．

旧

．

．

　

　

　

　　

　

　

　

　

　

　，

．

0

森

_．

　 　

L驢

1馳

．

0









L

_蝉・

　

　

　

．

r．

，

齟

・

「

．

　　　　　凶0　 舮 250H

．

．

．

匹

．

．

　 1

．

．

．

・

．

・

圜

一

．

一

hnag

．

　

　

　一

な

＝

500Hz jωF〔ω）eo1

，

2D

，

80

．

4O

．

0 　 0

．

−

0

，

4

一

〇

．

8 FREO凵ENCY　〔HZ， 〔e〕　Hc践「〔ω）

　

　

　

一

　！

_∠ ろ Rea【

・

。

，

な

＝

25H

・

　 　

枦

，

『

『

，

_．

　 

，

　

・

こ

・

．

布

＝

50Hz

　

　

　

　一一

4二

100H

・

．

一

罰

1．

r

0

．

．

−「

．

．

．

　　　 　50

．

O

　

　

　

　

　

　

　

　

　

　

　

r」

「

齟

　

　

　

　

　

　

　

　．

齟

」

」

　

　

　

　

L．

．．

」

齟

」

　

　

　

　

　

F．

「

　

　

齟

pr

齟

．

」

r齟

「

L°°

・

°

全

禦

聖

．

・

三呈D

　

　

　

．

．

．

囓

尸

．

，

．

．

．

「

．

　　

乙

琴

．

−

Imag

．

．

．

　　　　　　 

罩

ODHz

一

FREOUENCY　〔HZ｝ 　〔f）

．

Hm（ω）

Fig

．

_{6　Frequency}

．

dependent　characteristics 　H塁

．

〔ω）of ん翫［n］

地 盤剛 性 κo

＝

2

．

5× IO7　t／m

，

減 衰係 数 c。

＝

6

．

0× IOs t

・

sec _／m

_，

_{付 加 質 量 m 。}

；

₁

．

₆× 103　t

・

sec2 _／m で モ デル化 で き た場 合 を想 定し

，

時 刻 歴 応 答 解 析 手 法に関す る基 本 的 考 察を

，

速 度 定 式 化 を 中心 に行う

。

離 散 イン パ ル ス応 答の時 間 刻み △

t

をパ _ラメ

ー

タ と し て， Fig

．

2

のフロ

ー

か ら求 められる速 度 インパル ス応 答 を

Fig．

4 に 示す

。

また

，

離 散 イン パ ル ス応 答の初 期 値につ いて は変位イン パ ル ス応 答の初 期 値 と 比

・

tt

し て Fig

，

5

に示 し， 離散イ ン パ ル ス応 答 を周 波 数 領 域に変 換して得ら れ る

H

撫ω） を

Fig．

6に示す

。

な お

，

フ

ー

リエ _{項 数}N は

，

　 N△ tが

0

．

512sec ま た は

O．

64　sec と な る よう

．

に設 定し た。

．

（a_{）　 t}

＝

_{0近 傍}の挙 動 　本 例題の イン パ ル ス速 度 応 答は

，

前 述の よ うに因 果 的 で かつ

h

（t＝

O

＋_）≠0_であ る か ら

，h

_（t_｝は t

＝

O_{近 傍で不} 連 続 となっ てい る （

Fig．

4

（a））。 △ tを小

．

さ く して FFT を行う際のナイキス ト振 動 数

．

ん尋 ω

42

π を大き く す る こ と によ り

，

ん

ω

n

’

［n］は解 析 値

h

（t）に近づ い て い き

，

非 因 果 な 部 分 は t

＝

O近傍に近づ い て い くが_，

Gibbs

現 象とみ られ る細か な変 動が 顕著に見 ら れ る よ うに な る （

Fig．

4 （

b

））。 閃 果なインパル ス応 答 （Fig

．

4（c ）） を相 彑 に 比較す る と

，

△ tを小さ く す ることに より

，

離 散 イ ンパ ル ス応 答の差は不 連 続 点で あ る t

＝

0近傍に徐々 に 限 定され てい き

，t

の_増加にと も なっ て減 少 してい く傾 向が見ら れる。 また

，hr

［n］は

，

が

；O

の時

h

，［0］

＝h。

［0 ］

＝

0で あり

，

hr［ユ］は h（△

t

）（≠O）に近づ くか ら

，

．

t

≡

o近傍で Gibbs 現 象 を生じて お り，　 tの増 加に伴っ て振動

_レ

な が ら

h

〈t）に収 斂 して い

_，

〈

。

特に

，

△

t

’

が 大 き く な るにつ れて

，h

，［n］の波 形は

Gibbs

現象に埋 も れ て いき

，

h

（t）か ら 大 き くか け離れ て し ま う の で_，　 h ，［n］ の_{波 形}に対す る物 理 的な考 察を す ること が難し くな る

。

これに対 し て

，

妬 ［n］と 妬 ［n_］は

，

図で は なか な か 判 別で き ない ほど対

応

し た結果と な っ て お り

，

△ t間 隔の 各 離散点で

h

（t）と比 較して も

，

h｛

t

）が急 激に_変化 す る

t＝

0を除いて

h

（

t

）の_良い近 似 値と なっ ている

。

そ して

，

h

ω

。

［n］で見

．

ら れ た Gibbs 現象も 見ら れ な い

。

以 上の こ と か ら

，

動 的柔性が周 波 数帯域制 限さ れて い る場 合で も

，

実部だ け を用い て評 価さ れ る イン パ ル ス応 答 妬［n］を 用い る ことに よ り

，

過渡応 答に関 す る考 察が十 分 可 能で