A family of the Seiberg-Witten equations and configurations of embedded surfaces in 4-manifolds (Intelligence of Low-dimensional Topology)

A

_family

of the

_{Seiberg‐Witten equations}

and

_{configurations}

of

embedded surfaces in 4‐manifolds

Hokuto Konno

Graduate School of Mathematical

_Sciences,

the

_University

of

_Tokyo

Abstract

Inthispaperweconsider constraints on_{configurations consisting}offinitelymany surfacesem‐

bedded inan_{oriented closed 4‐manifold and its genera. Astudy}ofa_familyof theSeiberg‐Witten

equations,namely,the _{(high‐dimensional”}wallcrossingphenomenonplaysa_prominentrole inour

method. The results in§ 2arebasedon _[3].

1

The

_{adjunction inequalities}

and

_{configurations}

of embedded

surfaces with

_positive

intersection numbers

It is a fundamental

problem

in 4‐dimensional

topology

tofind a lower bound for the

genus of an embedded surface which _represents a

given

second

homology

class of a 4‐

dimensional manifold. This

_problem

is often called the minimal _genus

_problem.

For

example,

the minimal_genus

_problem

for

\mathbb{C}\mathbb{P}^{2}

is called the Thom

_conjecture

and this is

one of themostclassical

_problem

in4‐dimensional

_topology.

Gauge theory provides

strongtoolstoanswerthe minimal _genus

problem

andacertain

type of

_inequality

for _genus obtained

_by

_gauge

_theory

is often called the

_adjunction

in‐

equality.

Herewe

explain

this

terminology.

Let X be a

complex

surface and C asmooth

algebraic

curveinX. Then it is easy toseethat the Euler characteristic

$\chi$(C)=2-2g(C)

satisfies the

_equality

- $\chi$(C)=c_{1}(X)\cdot C+C^{2},

where means the intersection number and

C^{2}=C\cdot C

. This

equality

is called the

adJunction

formula.

When X is a C^{\infty}4‐manifold and a surface $\Sigma$ is embeddedto Xin

C^{\infty}_sense,

_then,

in

_general,

wecannotdetermine

_{g( $\Sigma$)}

_by

the

homology

class

_{[ $\Sigma$]}

.

However,

a

_surprising

observation in Kronheimer‐Mrowka

[4]

is

that,

for a suitable characteristic

c\in H^{2}(X;\mathbb{Z})

, one canexpectthe

inequality

- $\chi$( $\Sigma$)\geq|c\cdot[ $\Sigma$]|+[ $\Sigma$]^{2}.

After

_{Seiberg‐Witten}

_{theory appeared,}

it is

_successfully

usedto

_study

the minimal_genus

problem.

Kronheimer‐Mrowka

_[5]

_proved

the Thom

_conjecture

_{by using}

the

_Seiberg‐

Witten

_equations.

_They

gavethe wall

crossing

formula for the

_{Seiberg‐Witten}

invariants

for 4‐manifolds with b^{+}=1 and usethis formula for the

_proof

of the Thom

_conjecture.

Here

_b^{+}(X)

is the maximal dimension of

_positive

definite

_subspaces

of

_{H^{2}(X;\mathbb{R})}

with

respect totheintersection form ofX.

The direct consequence ofarguments in Kronheimer‐Mrowka

_[5]

is that the _strongre‐

lation between the

_{Seiberg‐Witten}

invariants and the

_{adjunction inequalities.}

For an

oriented,

closed smooth 4‐manifoldX with

_{b^{+}(X)\geq 2}

and a

spin

\mathrm{c} structure\mathfrak{s} onX, let

\mathrm{S}\mathrm{W}_{X}(\mathfrak{s})\in \mathbb{Z}

denote the

_{Seiberg‐Witten}

invariantofXwith_respect to\mathfrak{s}.

(More

precisely,

we have to fix a

homology

orientation of X to determine the

_sign

of

\mathrm{S}\mathrm{W}_{X}(\mathfrak{s})

. Here a

homology

orientation ofX means an orientationof

H^{0}(X;\mathbb{R})\oplus H^{1}(X;\mathbb{R})\oplus H^{+}(X;\mathbb{R})

,

where

_{H^{+}(X;\mathbb{R})}

is a b^{+}‐dimensional

_positive

definite

subspace

of

H^{2}(X;\mathbb{R}

In this

paper, we consider

_only

surfaces which are

oriented,

closed and connected. Put

$\chi$^{-}( $\Sigma$):=\displaystyle \max\{- $\chi$( $\Sigma$), 0\}

for asurface $\Sigma$.

Theorem 1.1.

_{(Kronheimer‐Mrowka [5])}

LetX be an

oriented,

closed smooth

4‐manifold

with

_{b^{+}(X)\geq 2}

and $\Sigma$ bea

surface

embeddedin X with

_{[ $\Sigma$]^{2}\geq 0}

. Lets be a

spin

cstructure

with

_{\mathrm{S}\mathrm{W}_{X}(\mathfrak{s})\neq 0}

.

Then,

the

inequality

$\chi$^{-}( $\Sigma$)\geq|c_{1}(\mathfrak{s})\cdot[ $\Sigma$]|+[ $\Sigma$]^{2}

holds.

However,

there are _many 4‐manifolds whose

Seiberg‐Witten

invariants vanish. Forex‐

ample,

the

_{Seiberg‐Witten}

invariants for 4‐manifolds obtained

by

connected sum vanish

under mild

_assumptions

on b^{+}: let

X_{i}(i=1,2)

be

oriented,

closed 4‐manifolds with

b^{+}(X_{i})\geq 1

, then

\mathrm{S}\mathrm{W}_{X_{1}\# X_{2}}(\mathfrak{s})=0

for any

spin

\mathrm{c} structure \mathfrak{s} on

X_{1}\# X_{2}

. Therefore

we cannot usethe

Seiberg‐Witten

invariant to show the

adjunction inequalities

for such

4‐manifolds. In

_fact,

Nouh

_[7]

_proved

that the

_{adjunction inequality}

for a surface in

\mathbb{C}\mathbb{P}^{2}\#\mathbb{C}\mathbb{P}^{2}

does not holdin

_general.

Nouh’s result shows

_that,

for such

_{4‐manifolds,}

not

only

does one cannotuse the

Seiberg‐Witten

invariants,

but also one _mayfind

examples

of surfaces which violate the

_adjunction

_{inequalities.}

Thus anatural

question

iswhenone canshowthe

adjunction inequality

for 4‐manifolds

whose

_{Seiberg‐Witten}

invariants vanish. In Strle’s paper

[12],

he showed the

following

adjunction inequalities

for

_disjoint

embeddedsurfaces with

_positive

self‐intersectionnum‐

Theorem 1.2.

_{(Strle [12])}

LetX beanoriented closed smooth

_4‐manifold

with

_{b_{1}(X)=0}

and

_{c\in H^{2}(X;\mathbb{Z})}

be a characteristic with

c^{2}>\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}(X)

.

(A)

In the case

of

b^{+}(X)=1

, let

$\alpha$\in H_{2}(X;\mathbb{Z})

be a

homology

class with

$\alpha$^{2}>0

and $\Sigma$\subset X be an embedded

surface

with

[ $\Sigma$]= $\alpha$

. Then the

inequality

- $\chi$( $\Sigma$)\geq-|c\cdot $\alpha$|+$\alpha$^{2}

(1)

holds.

(B)

In the case

of

b^{+}(X)>1

, let $\alpha$_{1},. ..

,

$\alpha$_{b+}\in H_{2}(X;\mathbb{Z})

be

homology

classes with

$\alpha$_{i}^{2}>0(1\leq i\leq b^{+})

and

$\Sigma$_{1}

,... _,

$\Sigma$_{b+}\subset X

be embedded

surfaces

with

[$\Sigma$_{i}]=$\alpha$_{i}.

Assume that

$\Sigma$_{1}

,.. ._,

$\Sigma$_{b+}

are

disjoint.

Then the

inequality

- $\chi$($\Sigma$_{i})\geq-|c\cdot$\alpha$_{i}|+$\alpha$_{i}^{2}

(2)

holds atleast one

i\in\{1, . . . , b^{+}\}.

Note that Strle’s theoremcanbe

applied

to4‐manifolds whose

Seiberg‐Witten

invariants

vanish. His result _suggests that one can _expect some constraints on

configurations

of

embedded surfacesina 4‐manifold evenwhen its

Seiberg‐Witten

invariant vanishes. In therestof this_paper, wewill

explain

twoconstraintson

configurations

of embedded

surfaces with self‐intersection number zero. Our constraints can be also

applied

to 4‐

manifolds whose

_{Seiberg‐Witten}

invariantsvanish. While Strle’s

proof

standson a

study

of the moduli _space of the

_{Seiberg‐Witten equations}

on a 4‐manifold with

cylindrical

ends,

ourmethod is to

_{study only}

_compact 4‐manifolds and use the

“high‐dimensional”

wall

_crossing

_phenomena.

In

_{Seiberg‐Witten}

_theory,

the wall

_{crossing phenomena}

are

usually

studied in the case when b^{+}=1. Li‐Liu

[6]

gave its

generalizations

for any

b^{+}. While in the usual wall

crossing

phenomena

a

1‐parameter

family

of the

Seiberg‐

Witten

_equations

is the main

_object,

in Li‐Liu

_[6]

’s situation a b^{+}_‐parameter

family

is

it. We call Li‐Liu

_[6]

’s

_{generalizations}

the

_{high‐dimensional}

wall

_{crossing phenomena.}

To

use the

high‐dimensional

wall

crossing

phenomena

for constraints on

configurations,

in

[3]

the author gave a sufficient condition on a certain b^{+}‐parameter

family

to catch the

high‐dimensional

wall

_crossing

_phenomenon

in terms of embedded surfaces. This is the foundation of the

_proof

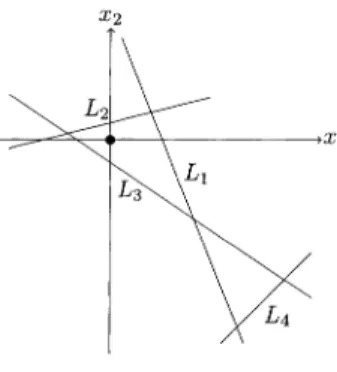
ofthe results inthis_paper.

Figure1: An_exampleofa_{quadrilateral including}theoriginof\mathbb{R}^{2}

2

Constraints

on

configurations

obtained

by

the

high‐dimensional

wall

_{crossing phenomena}

Inthis

_section,

we

explain

a

special

caseof the result obtained

by

the

high‐dimensional

wall

_{crossing phenomena,}

_namely,

the

_{adjunction inequalities}

for

_{configurations}

ofsurfaces

in

2\mathbb{C}\mathbb{P}^{2}\# n(-\mathbb{C}\mathbb{P}^{2})

. For a

generalization

of this

result,

see

[3]. (From

the

general

form of our

results,

we can

_give

a

simple

alternative

proof

of Strle’s results: Thoerem

1.2.)

We

will oftenuse theidentification H^{2}

\simeq H_{2}

obtained

_by

Poincaré

_duality.

Let consider the 4‐manifold

X=2\mathbb{C}\mathbb{P}^{2}\# n(-\mathbb{C}\mathbb{P}^{2})=(\#_{p=1}^{2}\mathbb{C}\mathbb{P}_{p}^{2})\#(\#_{q=1}^{n}(-\mathbb{C}\mathbb{P}_{q}^{2})) (n>0)

.

Let

_{H_{p}}

denote a _generator of

H_{2}(\mathbb{C}\mathbb{P}_{p}^{2};\mathbb{Z})

and

E_{q}

a _generator of

H_{2}(-\mathbb{C}\mathbb{P}_{q}^{2};\mathbb{Z})

. For a

cohomology

class

_{c\in H^{2}(X;\mathbb{Z})}

and

_homology

classes$\alpha$_{1},..._,

$\alpha$_{4}\in H_{2}(X;\mathbb{Z})

_, we definea

line

_{L_{i}(i=1, \ldots, 4)}

in\mathbb{R}^{2}

by

L_{i} :=\{(x_{1}, x_{2})\in \mathbb{R}^{2}|(x_{1}H_{1}+x_{2}H_{2})\cdot$\alpha$_{i}=c\cdot$\alpha$_{i}\}

.

(3)

For these

_lines,

we will consider the condition that

(parts of)

lines

L_{1}

,.. ._,

L_{4}

form sides

ofa

“quadrilateral by

this order. Herewe usethe word

(‘quadrilateral

inthe

following

sense. Let

Lí,

. .. _,

L_{4}'

be four line segments in \mathbb{R}^{2}. Ifan orientation of

Lí

is

given,

we candefine the initial

_point

I(L_{i}')

and the terminal

_point

T(Lí)

of

Lí.

We call the ordered

set

_(Lí,

.. .

,

L_{4}')

a

quadrilateral

when there exists an orientation for each

Lí

such that

T(Lí)

=I(L_{i+1}')

holds for each

_{i\in \mathbb{Z}/4}

.

(We

admit a

point

as a line

segment.

Thus a

“triangle”

alsoa

quadrilateral

inour

definition.)

Theorem 2.1. For the

_4‐manifold

let

_{c\in H^{2}(X;\mathbb{Z})}

be a characteristic with

c^{2}>\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}(X)

and _{$\alpha$_{1}},. .._,

$\alpha$_{4}\in H_{2}(X;\mathbb{Z})

be

homology

classes with

_{$\alpha$_{i}^{2}=0(i=1, \ldots, 4)}

. Let

$\Sigma$_{1}

_,.. .

,

$\Sigma$_{4}\subset X

be embedded

surfaces

with

_{[$\Sigma$_{i}]=$\alpha$_{i}}

. Assume that$\alpha$_{i} andc

satisfy

the

following

(A)

and

$\Sigma$_{i}

satisfy

(B)

:

(A)

The lines

L_{1}

,... _,

L_{4}

form

sides

of

a

quadrilateral including

the

origin

of

\mathbb{R}^{2}

by

this

order.

(B) $\Sigma$_{i}\cap$\Sigma$_{i+1}=\emptyset(i\in \mathbb{Z}/4)

.

Then,

the

_inequality

- $\chi$($\Sigma$_{i})\geq|c\cdot$\alpha$_{i}|

holds

_for

at least one

i\in\{1

,..._,4

\}.

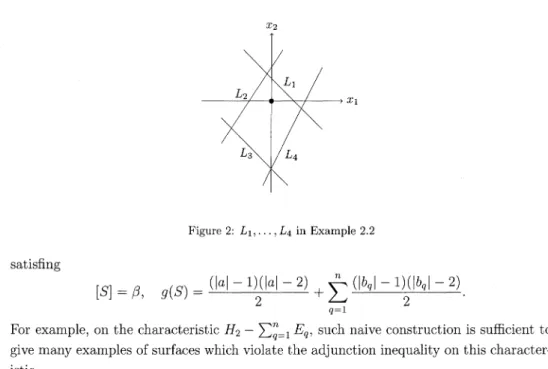
Example

2.2. Let

_{X=2\mathbb{C}\mathbb{P}^{2}\# 19(-\mathbb{C}\mathbb{P}^{2})}

,

c=H_{1}-3H_{2}-\displaystyle \sum_{q=1}^{19}E_{q}

. The

homology

classes

$\alpha$_{1} :=3H_{1}+3H_{2}-\displaystyle \sum_{q=1}^{3}E_{q}+\sum_{q=4}^{10}E_{q}+2(E_{11}+E_{12})

,

$\alpha$_{2} :=-3H_{1}+2H_{2}+\displaystyle \sum_{q=1}^{3}E_{q}+\sum_{q=13}^{18}E_{q}+2E_{19}

$\alpha$_{3}:=H_{1}+H_{2}+E_{12}-E_{13},

$\alpha$_{4} :=2H_{1}-H_{2}-\displaystyle \sum_{q=1}^{3}E_{q}-E_{13}+E_{14}

satisfy

that

_{$\alpha$_{i}^{2}=0}

and

_{$\alpha$_{i}\cdot$\alpha$_{i+1}=0(i\in \mathbb{Z}/4)}

. It is easy to check that these $\alpha$_{i} and c

satisfy

(A)

inTheorem 2.1.

_(See

_Figure

_2.)

Thus,

by

Theorem

_2.1,

for embedded surfaces

_{$\Sigma$_{i}}

_satisfying

_{[$\Sigma$_{i}]=$\alpha$_{i}}

, if

they

also

satisfy

that

_{$\Sigma$_{i}\cap$\Sigma$_{i+1}=\emptyset(i\in \mathbb{Z}/4)}

,

- $\chi$($\Sigma$_{i})\geq|c\cdot$\alpha$_{i}|

holds for at leastone

i\in\{1

,. .._,4

\}

. Thismeans that thegenus bound

g($\Sigma$_{i})\geq 2

holds for at leastone

i\in\{1

,... _,4

\}.

Undercertain

_assumptions

on

geometric

intersectionswith embedded surfaces

violating

the

_{adjunction inequalities,}

we can derive the

adjunction inequality

for a

single

surface.

Before

_giving

an

example,

wementionan_easymethodtomakesurfaces with smallgenera.

Fora

homology

class

$\beta$=aH_{2}+\displaystyle \sum_{q=1}^{n}b_{q}E_{q}\in H_{2}(\mathbb{C}\mathbb{P}_{2}^{2}\# n(-\mathbb{C}\mathbb{P}^{2});\mathbb{Z})

,

considering algebraic

curves

C\subset \mathbb{C}\mathbb{P}_{2}^{2}

and

C_{q}\subset \mathbb{C}\mathbb{P}_{q}^{2}

and

reversing

orientations of them ifwe

need,

we can

easily

construct the surface

_{S\subset \mathbb{C}\mathbb{P}_{2}^{2}\# n(-\mathbb{C}\mathbb{P}^{2})}

_by

Figure2: L_{1},..._,L_{4}inExample2.2

satisfing

[S]= $\beta$, g(S)=\displaystyle \frac{(|a|-1)(|a|-2)}{2}+\sum_{q=1}^{n}\frac{(|b_{q}|-1)(|b_{q}|-2)}{2}.

For

_example,

on the characteristic

H_{2}-\displaystyle \sum_{q=1}^{n}E_{q}

, suchnaive construction is sufficient to

give

many

examples

of surfaces which violate the

adjunction inequality

onthischaracter‐

istic.

Example

2.3. Let

_give

natural numbers

_{d_{1}\geq 4, d_{2}\geq 1, d_{3}\geq 2}

and

_{n\displaystyle \geq d_{1}^{2}+\max\{d_{2}^{2}, d_{3}^{2}\}.}

For

_{X=2\mathbb{C}\mathbb{P}^{2}\# n(-\mathbb{C}\mathbb{P}^{2})}

,let consider the

homology

classes

$\alpha$:=d_{1}H_{1}-\displaystyle \sum_{q=1}^{d_{1}^{2}}E_{q},

$\beta$_{1}:=d_{2}H_{2}+\displaystyle \sum_{q=d_{1}^{2}+1}^{d_{1}^{2}+d_{2}^{2}}E_{q},

$\beta$_{2}:=d_{3}H_{2}-\displaystyle \sum_{q=d_{1}^{2}+1}^{d_{1}^{2}+d_{3}^{2}}E_{q}.

Let

_{S_{i}\subset \mathbb{C}\mathbb{P}_{2}^{2}\# n(-\mathbb{C}\mathbb{P}^{2})\backslash (}

_disk)

\subset X be surfaces with

_{[S_{i}]=$\beta$_{i}}

obtained as

(4).

Foran

embedded surface $\Sigma$\subset X

satisfying

[ $\Sigma$]= $\alpha$

and

_{$\Sigma$\cap S_{i}=\emptyset(i=1,2)}

, we can show that

g( $\Sigma$)\displaystyle \geq\frac{(d_{1}-1)(d_{1}-2)}{2}

(5)

from Theorem 2.1.

By

the

_adjunction

formula for

_{\mathbb{C}\mathbb{P}_{1}^{2}\# n(-\mathbb{C}\mathbb{P}^{2})}

,the

homology

class $\alpha$ canbe

represented

by

asurface $\Sigma$ ofgenus

(d_{1}-1)(d_{1}-2)/2

satisfying $\Sigma$\cap S_{i}=\emptyset

. Thus the

inequality

(5)

3

Constraints

on

configurations

obtained

by

the

high‐dimensional

wall

_{crossing phenomena}

and the

_{gluing technique}

To obtain the results in

_{§ 2,}

the author used the

_{high‐dimensional}

wall

_{crossing phe‐}

nomena in

[3].

On the other

hand,

Ruberman

([8], [9]

and

[10])

studied the combination

of the usual

_{(\mathrm{i}.\mathrm{e}. b^{+}=1)}

wall

_crossing

_phenomena

and the

_{gluing technique.}

The

_gluing

technique

is a

deep analytical

tool in gauge

theory.

A

typical application

of the

gluing

technique

isthe

_proof

the

_blowup

_formula,

which describes the behavior of the

Seiberg‐

Witten invariants

_(or

Donaldson

_invariants)

under

_blowups

of 4‐manifolds. Ruberman’s

argumentscanbe

regarded

as a

1‐parameter

version of the

proof

of the

blowup

formula.

Namely,

Ruberman considered the

_gluing

_argument asthe

proof

of the

blowup

formula for

the

_{1‐parameter}

_family

touse the wall

crossing

_argument. This _argument can be _gener‐

alizedto

_{higher‐dimensional}

familiestousethe

high‐dimensional

wall

crossing

_argument.

This

_{generalization gives}

new constraints on

configurations.

In this

_section,

we

_give

the

formulation of these results.

To describe the

_results,

for a

spin

c4‐manifold,

we introduce an abstract

simplicial

complex

which consists of surfaces

_violating

the

_adjunction

_{inequalities.}

Before the defi‐

nitionof this

_{simplicial complex,}

weneedan ‘(ambient”

simplicial complex.

This ambient

simplicial complex

wasintroduced tothe author

_by

Mikio Furuta.

Definition 3.1.

_(Furuta)

For an

oriented,

closed 4‐manifold X, we define the abstract

simplicial complex

_{\mathcal{K}=\mathcal{K}(X)}

asfollows:

The set ofvertices

_{V(\mathcal{K})}

is

_given

as the set of smooth

_embeddings

ofsurfaces with

self‐intersection number zero:

V(\mathcal{K}):=\{ $\Sigma$\mapsto X|[ $\Sigma$]^{2}=0\}.

Here we consider

only oriented, closed,

connected surfaces. We denote each vertex

( $\Sigma$\leftarrow+X)\in V(\mathcal{K})

briefly by

$\Sigma$.

For

k\geq 1

, a collection of

(k+1)

vertices

$\Sigma$_{0}

,. .._,

$\Sigma$_{k}\in V(\mathcal{K})

spans a k

‐simplex

if

and

_only

if

$\Sigma$_{0}

,... _,

$\Sigma$_{k}

are

disjoint.

Wecall \mathcal{K} the

_{complex of surfaces}

of X.

Of_{course, any}abstract

_{simplicial complex}

is a CW

complex,

thus \mathcal{K}is a CW

complex

although

\mathcal{K}isa

huge

_space.

Wetopologize

\mathcal{K}as aCW

complex, i.e.,

by

the weak

topology.

Remark3.2. The

_complex

of surfacesis a4‐dimensional

analog

of the

complex

of curves

due to

_Harvey

_[2]

in 2‐dimensional

_topology.

In the above definition of the

complex

of

hand,

in the same _way of the definition of the

complex

of_curves, one can define an ab‐

stract

_{simplicial complex}

whoseverticesarethe

isotopy

classesof

embeddings

of surfaces

and whose

_simplices

are

spanned by

collections of such

isotopy

classes whichcan bereal‐

ized

_{disjointly. However,}

to

_give

certain

_applications

to the

_{adjunction inequalities using}

Seiberg‐Witten theory,

the first definition of the

_complex

of surfaces

_might

be

_appropriate.

Hereweconsider the

special phenomena

in4‐dimensional

topology, namely,

the

adjunc‐

tion

_{inequalities.}

Definition 3.3. Let\mathfrak{s}bea

spin

\mathrm{c}structureonX.

Then,

the

complex

of surfaces violating

the

_{adjunction inequality}

_{\mathcal{K}_{V}=\mathcal{K}_{V}(X, \mathfrak{s})}

is the

_subcomplex

of

_{\mathcal{K}(X)}

definedas theset of

vertices is

_given

_by

V(\mathcal{K}_{V}):=\{ $\Sigma$\in V(\mathcal{K})|$\chi$^{-}( $\Sigma$)<|c_{1}(\mathfrak{s})\cdot[ $\Sigma$]|\}

and

_having

the induced structure of an abstract

simplicial complex

from \mathcal{K}.

Namely,

$\Sigma$_{0}

,... _,

$\Sigma$_{k}\in V(\mathcal{K}_{V})

spans a k

‐simplex

if and

only

if

$\Sigma$_{0}

_,. .._,

$\Sigma$_{k}

spana k

‐simplex

in \mathcal{K}.

Let \mathrm{s}^{+} be a

spin

\mathrm{c}structure on

\mathbb{C}\mathbb{P}^{2}

such that

c_{1}(\mathfrak{s}^{+})

isa _generator in

H_{2}(\mathbb{C}\mathbb{P}^{2};\mathbb{Z})

and

\mathfrak{s}^{-} be a

spin

\mathrm{c} structureon

-\mathbb{C}\mathbb{P}^{2}

such that

c_{1}(\mathfrak{s}^{-})

is a _generatorin

H_{2}(-\mathbb{C}\mathbb{P}^{2};\mathbb{Z})

.

(We

havetwochoices of each\mathfrak{s}^{+} and\mathfrak{s}

The mainresult inthis section isthe

_following

statement.

Theorem 3.4. Let

_{(X, \mathrm{s}_{X})}

be an

oriented,

closed

_spin

c4

‐manifold

with

b^{+}(X)\geq 2.

Suppose

that

_{\mathrm{S}\mathrm{W}_{X}(\mathfrak{s})\neq 0}

and

_{d(\mathfrak{s}_{X})=0}

, where

d(\mathrm{s})

:=(c_{1}(\mathfrak{s})^{2}-2 $\chi$(X)-3\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}(X))/4.

Put

Z:=X\# m\mathbb{C}\mathbb{P}^{2}\# n(-\mathbb{C}\mathbb{P}^{2}) (m\geq 1, n\geq 4m)

,

\mathfrak{s}_{Z}:=\mathfrak{s}_{X}\#(\#_{p=1}^{m}\mathfrak{s}_{p}^{+})\#(\#_{q=1}^{n}\mathfrak{s}_{q}^{-})

.

Then

\tilde{H}_{m-1}(\mathcal{K}_{V}(Z, \mathfrak{s}_{Z});\mathbb{Z})\neq 0

holds.

Remark 3.5. More

_precisely,

wecan

_give

aconcretenon‐trivial element of

\tilde{H}_{m-1}(\mathcal{K}_{V}(Z, \mathfrak{s}_{Z});\mathbb{Z})

.

To_prove Theorem

_3.4,

wedefine a_group

homomorphism

SW

_{=\mathrm{S}\mathrm{W}_{Z,\mathfrak{s}_{Z}}:\mathcal{H}_{*}(Z,\mathfrak{s}_{Z})\rightarrow \mathbb{Z}}

and show that thismap isnon‐tivial. Here

\mathcal{H}_{*}(Z,\mathfrak{s}_{Z})

isacertain

subgroup

of

\tilde{H}_{*}(\mathcal{K}_{V}(Z, \mathfrak{s}_{Z});\mathbb{Z})

.

The _mapSWis

_{defined, roughly speaking, by “counting”}

the

_parametrized

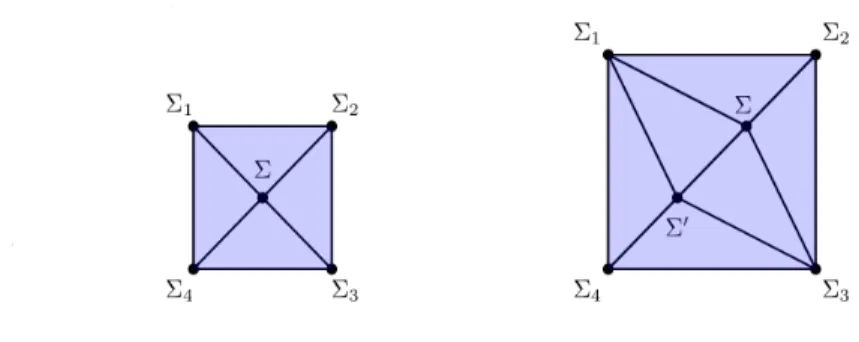
modulispace

Figure3: Some_boundingsfor _$\gamma$

counting

argument, we useRuan’s virtual

neighborhood

technique

andits

family

version.)

This_{parameterspace}isobtained

_{by stretching}

_{neighborhoods}

of embedded surfaces which forms the element of\mathcal{H}_{*}. Thisconstructionof the

parameter

spaceis a

slight

generaliza‐

tion ofonedueto\mathrm{F}\mathrm{r}\emptyset

yshov

[

1]

. The

proof

of the

non‐triviality

of this mapis

given

by

the

combination of the

_{high‐dimensional}

wall

_crossing

_phenomena

and the

_gluing

technique.

Here we

explain why

a non‐trivial element of

\tilde{H}_{*}(\mathcal{K}_{V}(Z, \mathfrak{s}_{Z});\mathbb{Z})

is useful to

_give

con‐

straintson

configurations

of embedded surfaces andits genera. For

example,

let

$\Sigma$_{1}

,... _,

$\Sigma$_{4}\in

V(\mathcal{K}_{V})

be embedded surfaces with

_{$\Sigma$_{i}\cap$\Sigma$_{i+1}=\emptyset(i\in \mathbb{Z}/4)}

. Then the collection

\{($\Sigma$_{i}, $\Sigma$_{i+1}\}\}_{i\in \mathrm{Z}/4}

formsa

1‐cycle

$\gamma$=\{$\Sigma$_{1}, $\Sigma$_{2}\}+\cdots+\langle$\Sigma$_{4}, $\Sigma$_{1}\rangle

in

\mathcal{K}_{V}

. Assume that

[ $\gamma$]\neq 0

in

_{H_{1}(\mathcal{K}_{V};\mathbb{Z})}

. For

$\Sigma$\in V(\mathcal{K})

with

$\Sigma$\cap$\Sigma$_{i}=\emptyset(i\in \mathbb{Z}/4)

_,the collection

\{\langle $\Sigma,\ \Sigma$_{i}, $\Sigma$_{i+1})\}_{i\in \mathbb{Z}/4}

can be

regarded

as the “cone” of this

1‐cycle.

(See

Figure

3.)

If

$\Sigma$\in V(\mathcal{K}_{V})

holds,

this

“cone” iscontainedin

_{\mathcal{K}_{V}}

, thus

[ $\gamma$]=0

in

H_{1}(\mathcal{K}_{V};\mathbb{Z})

. This contradictsour

assumption,

thereforewe have

$\Sigma$\not\in V(\mathcal{K}_{V})

. In

conclusion,

we have the

adjunction inequality

for an

embedded surface $\Sigma$ with

_{$\Sigma$\cap$\Sigma$_{i}=\emptyset(i\in \mathbb{Z}/4)}

.

Inthesame _way,for embedded surface

$\Sigma$,

$\Sigma$'\in V(\mathcal{K})

,if $\Sigma$ and $\Sigma$' satisfies

$\Sigma$\cap$\Sigma$_{i}=\emptyset(i=1,2,3) , $\Sigma$'\cap$\Sigma$_{i}=\emptyset(i=1,3,4) , $\Sigma$\cap$\Sigma$'=\emptyset,

then

_{$\Sigma$\not\in V(\mathcal{K}_{V})}

or

$\Sigma$'\not\in V(\mathcal{K}_{V})

holds.

Namely,

the

adjuction

inequality

holds for $\Sigma$ or

$\Sigma$'.

(See

Figure

3.)

Asinthese

_example,

ifwefindanon‐trivial elementin

H_{*}(\mathcal{K}_{V};\mathbb{Z})

,weobtain constraints

on_generafor

infinitly

_many

configurations

of surfaces.

Acknowledgement.

The author wouldliketo express his

deep

gratitude

to Mikio Furuta

for thenumerouscommentsonthis work. The authorwas

supported by

JSPS KAKENHI

References

[1] Kim A.\mathrm{F}\mathrm{r}\emptyset_yshov, An_{inequality for}the h ‐invariant in instanton Floer_{theory,Topology}43(2004),no. _2,407‐432,

DOI 10.1016/\mathrm{S}0040-9383(03)00049-1 MR2052970(2005c:57043)

[2] W. J._{Harvey, Boundary}structureofthemodulargroup, Riemannsurfacesand relatedtopics:Proceedingsof the 1978

StonyBrookConference_(StateUniv.NewYork, Stony Brook,NY., 1978),Ann. of Math Stud.,vol.97,Princeton

Univ.Press, Princeton, N.J., 1981,pp. 245‐251. MR624817

[3] H.Konno,Boundson_genusand_{configurations of}embedded_surfacesin4‐manifolds,available at arXiv: 1507. 00139.

[4] P. B. Kronheimer and T. S.Mrowka,Embedded_surfacesand the structure_ofDonaldson’s_{polynomial invariants,}\mathrm{J} Differential Geom. 41_(1995),no._3,573‐734. MR1338483_(96e:570l9)

[5] —, The genus ofembeddedsurfaces in theprojective plane,Math. Res. Lett. 1 (1994), no. 6, 797‐808, DOI

10.4310/\mathrm{M}\mathrm{R}\mathrm{L}.1994.\mathrm{v}1n6a14. MR1306022(96a:57073)

[6] Tian‐JunLiand Ai‐Ko_{Liu, Family Seiberg‐Witten} invariants andwallcrossingformulas, Comm.Anal. Geom. 9

(2001),no.4,777‐823. MR1868921_{(2002k:57074)}

[7] MohamedAitNouh,The minimal genusproblemin_{\mathbb{C}\mathrm{P}^{2}\#\mathbb{C}\mathrm{P}^{2}},Algebr.Geom.Topol.14(2014),no.2, 671‐686,DOI

10._{2140/\mathrm{a}\mathrm{g}\mathrm{t}.2014.14.671}. MR3159966

[8] Daniel_Ruberman,Anobstruction tosmooth_isotopyin dimension_4,Math.Res. Lett. 5_(1998), no._{6, 743‐758,}DOI 10._{4310/\mathrm{M}\mathrm{R}\mathrm{L}.1998}v5 n6 a5. MR1671187(2000c:5706l)

[9]—, A polynomial invar\cdot $\iota$ ant of diffeomorphisms of 4‐manifolds, Proceedings of the Kirbyfest (Berkeley,

CA, 1998), Geom. Topol. Monogr., vol. 2, Geom Topol. Publ., Coventry, 1999, pp. 473‐488 (electronic), DOI

10._{2140/\mathrm{g}\mathrm{t}\mathrm{m}.1999.2.473}. MR1734421(2001b:57073)

[10]—,Positivescalar curvature, diffeomorphismsandtheSeiberg‐Witten invariants,Geom.Topol.5(2001),895−924

(electronic),DOI 10._{2140/\mathrm{g}\mathrm{t}.2001}5.895.MRIS74146(2002k:57076)

[11] Yongbin Ruan,Virtualneighborhoodsand themonopole equations, Topicsinsymplectic4‐manifolds(Irvine,CA,1996),

First Int. Press Lect.Ser., I,Int.Press,Cambridge, MA, 1998,pp. 101‐116. MR1635698(2000e:57054)

[12] SašoStrle,Boundson_genusand_geometricìntersectionsfrom cylindricalend moduli spaces, J.DifferentialGeom. 65

(2003),no.3,469‐511. MR2064429(2005c:57042)

Graduate School of Mathematical Sciences The

_University

of

_Tokyo

3‐8‐1

_{Komaba, Meguro, Tokyo}

153‐8914

JAPAN

\mathrm{E}‐mail address:

_{hkonno@ms.u‐tokyo.ac.jp}