AN EVOLUTIONARY THEORY OF CONFLICT RESOLUTION BETWEEN RELATIVES : ALTRUISM, MANIPULATION, COMPROMISE(Mathematical Topics in Biology)

AN

EVOLUTIONARY THEORY OF CONFLICT

RESOLUTION

BETWEEN RELATIVES:

ALTRUISM, MANIPULATION,

COMPROMISE

Norio Yamamura (山村則男)

DepartmentofNatural Sciences, Saga Medical School, Nabeshima, Saga 849,Japan

and

Masahiko Higashi (東正彦)

Faculty ofScienceandTechnology, Ryukoku University, Seta, Otsu520-21, Japan

Many

cases

of conflict between relatives

over

the evolution of social behavior

are

known ($e$

.

_$g.$,Dawkins, 1976; Trivers, 1985), but

no

generaltheory incorporates the

consequences

ofconflict. Here

we

show how compromise solutions

may

evolve. We derive the compromise solutionbyincoIporating conflictcosts into the fitness

evaluation. Specifically, for donor-recipientconflict concemingaltruism,

we

find thataltruismevolves

more

easily thanHamilton’sRule(Hamilton, 1964)_would

predict forthe

case

with

no

effective manipulation bytherecipient, whereas in the

opposite case, where the donor camotresist therecipient’s manipulation, the behavior evolves less easily than the Inverse Hamilton’s Rule would predict. The theory also indicates conditions under which

no

compromise is reached, and physical conflictis manifested.

For the Hymenoptera, ithas been debated whetherthe evolution of sterile workercastes is duetokin selection fordaughters’ $al\alpha uistic\sim$behavior towardtheir mother(Hamilton, 1964),

or

to the development ofthe mother’s manipulation which forces “unwiUing” daughters to

serve

her(Alexander, 1974; Chamov, 1978).

Trivers (1974) considered the problem of parent-offspring conflict

over

parental

invesmlent. In

many

cases

besides these the

existence

of conflicthas been stressed,

butthere hasbeen remarkably little work

on

theimportant problem of where the

conflict should lead. As in the

case

of mother-daughterconflict inthe evolution of sterile workers, settlement ofthe conflict has been consideredto be simply

a

matter

ofconquest by the stronger (e.g.,mother’s

manipulation).

But both sides engaged in

any

conflict

are

expected to

pay

some

cost, and if the costs

are

taken into

account, it

seems

that the outcome shouldbe affected bynot only the relative

strengths oftheplayers, but also by theirrelative benefits (or losses) _whentheywin

(or lose)the conflict.

Here

we

present

a

general scheme by which rules

may

be derived for the

conflict. Akey idea inthis scheme is the incorporation ofconflictcosts into the inclusive fitness evaluation. We illustrate the general scheme,using

as a

model

case

the donor-recipient conflict

over

the evolutionofaltruisticbehavior.

Consider the evolution of

an

altruistic behavior by the donor(hereafterreferred

to

as

D) _{that decreases its}

own

_{fitness by}$C$and increases by$B$the fitness of the

recipient (hereafter R). A symmetricgenetic relation between$D$ and $R$is assumed

with degree of relatedness $r$

.

The condition for the altruistic behavior of$D$ (without

$R’s$ control) tobe favoured by selectionis thatthe inclusive fimess of$D$ is greater

whenit perfonns this altruistic behavior than whenit does not: $W_{D^{-}}C+rB>W_{D}$,

where $W_{D}$ is $D’ s$ fitness without

any

social interaction (Hamilton, 1964). Fromthis,

Hamilton‘sRule immediately follows:

$\frac{B}{C}>\frac{1}{r}$

.

(1)

On the otherhand, the condition for this altruisticbehavior to increase$R’s$

inclusive fimess is $W_{R}+B+r(- C)>W_{R}$, _where $W_{R}$ is $R’s$ fitness without

any

social

interaction.

From this follows

a

differentrelationship,

旦$>$ _’

(2)

which

may

be called the Inverse Hamilton‘s Rule. Even if the recipientcould force the donortoperfonn the altruistic behavior, the recipient shouldnot do

so

when

condition (2)_does nothold.

The

gap

between conditions (1) _and (2) implies

a

conflict. If$B/C$lies between$r$

and $1/r$ , i.e.,

$r< \frac{B}{C}<\frac{1}{r}$

then$D$ shouldnotperfonn the altruistic behavior [because condition(1) does not

hold], whereas $R$ should attempt to make$D$ perfonn;he altruistic behavior

[because condition (2) doeshold] (seeFig. 1). _{Notice that the conflict regionis}

reducedwith$r$,banishing when $r=1$; thereexists

no

conflictbetween genetically

identicalindividuals. Onthe contrary, when $r=0$, the $con^{b}flict$regionexpands to

the whole regionofpositive values of$B$ and$C$

.

However, ifcosts involved in theconflict

are

takeninto accountin the inclusive

fitness evaluation, then this potential conflict

may

have

an

evolutionaryresolution.

Here, by costs involvedinthe conflict,

we mean

reduction inthe fimess ofthe recipient inmanipulating the donor and that of the donorin resisting againstthe recipient’s control. Thereexists in the $(C, B)$

-space

a

critical line that divides the

conflictregiondefined by condition (3) _intotwo sub-regions. Inthe sub-region

above the line the donorisselected to avoid conflictby perforning thealtruistic

behavior, whereas in the sub-region belowthe line the recipient shouldavoid

conflictbynotattempting tomanipulate the donor. Tluis compromiseline forthe

donor-recipient conflictis

$\frac{B}{C}=\frac{2kr+r^{2}+1}{k(r^{2}+1)+2r}$ (4)

Aderivation follows.

Suppose thatparameters $(C, B)$ take values thatfallinthe conflictregion defined

by condition (3). Let$d_{D}$ and$d_{R}$,respectively, denote the costspaid by $D$ and$R$ in

pursuing theconflict, and

assume

that $R$win dominate $D$inthe conflict when_{$u_{R}>$}

$d_{D}$,whereas $D$ will dominate $R$when$kd_{R}<d_{D}$

.

Thatis, inorder for$D$to

resist

$R$,

it

has to

pay

$k$times

as

much cost

as

$R$ does; thus,$k$represents the degree of

Then, $D$ and$R$ willevolveto increase theirconflict costs inorderto rival each

other. When they build theircosts

up

to $d_{D}(=u_{R)}$ and$d_{R}$, respectively, the

inclusive fitness that $D$ would

eam

in the

case

ofwinning the conflict should be

reduced to $W_{D}- kd_{R}+r(- d_{R})$, and that of$R$ to _{$W_{R}- d_{R}+B+r(- C- kd_{R})$}

.

(Note

that the costofconflictpaid by

one

side contributes

a ne

ative effecttonot onlv its

own

fitness. but also to the other’s inclusivefimess through theirrelatedness $r.$) As the conflictcosts $(d_{R})$ increase,the inclusive fitness of$D$ (or R) will decline toward

the value thatit would take ifit yieldedto the otherinthefirst place. Eventually, the better choice for $D$ (or R) is to yield to $R$(or D), and the altruistic behavior will (orwillnot)evolve.

Theconditionthat$D’s$ inclusive fitness value in the

case

ofwinning is greater

than itwould be in the

case

ofavoiding theconflict inthe firstplace is given

as

$W_{D}-$

$kd_{R}+r(- d_{R})>W_{D}- C+rB$,

or

equivalently

$Ckd_{R}^{R}B_{-}+d< \frac{1}{r}$

(5)

The

same

condition for$R$ is given

as

$W_{R}- d_{R}+$$B+r$(-C- $kd_{R}$) $>W_{R}$,

or

equivalently

$\frac{B- d_{R}}{C+kd_{R}}<r$

.

(6)

[For

a

geometric interpretation in$(C, B)$

-space

of conditions (5) and (6),

see

Fig. 1

and its legend.]

Therefore, the conditionthat$D$ should yield to $R$ andperforn the altruistic

behavior is that for

some

$d_{R}$, both sides of condition (5) becomeequal toeach

other, while inequality (6) stillholds. Eliminating $d_{R}$ from thesetwo conditions,

we

$\frac{B}{C}>\frac{2kr+r^{2}+1}{k(r^{2}+1)+2r}\equiv g(r, k)$

.

(7)

Likewise, the condition for$R$to yieldto$D$ andnot attempt to inducethe altruistic

behavioris givenby inequality (7)_{withthe opposite inequalitysign}$(<)$

.

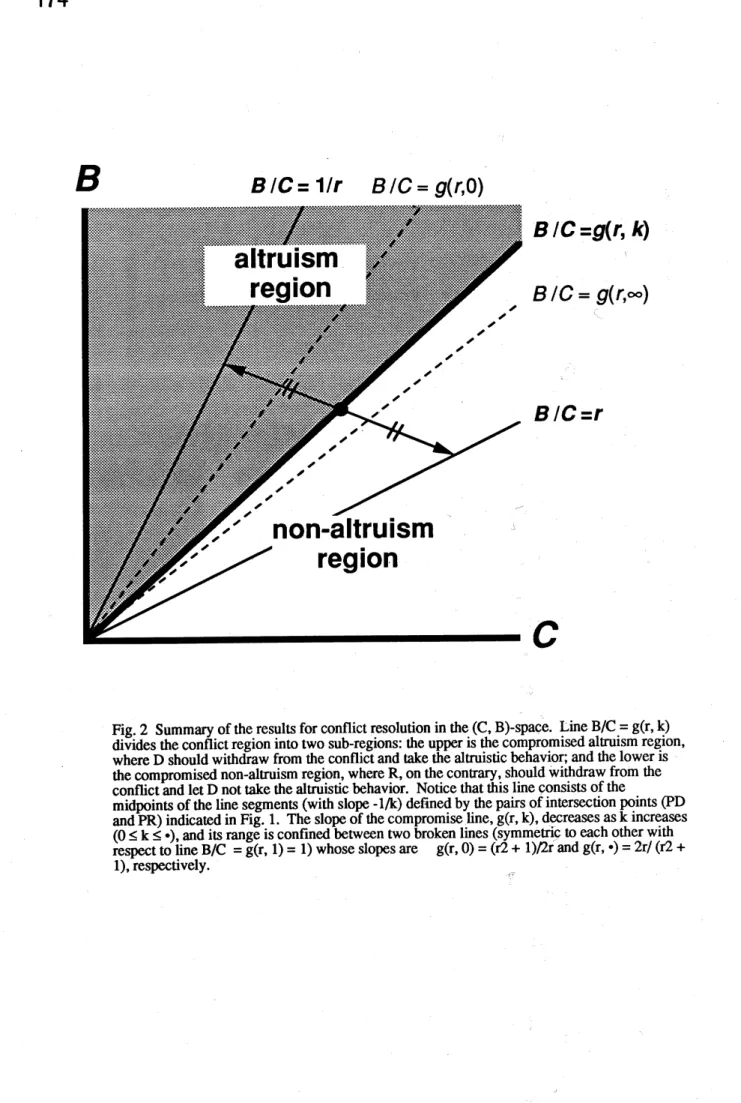
Therefore,

the compromise line, whichrepresents the criticalcondition for the evolution of the altruisticbehavior, is givenbyequation(4) (Fig.2).

$J$

$7he$ slope of the compromiseline, $g(r, k)$, _{decreases with}increasing $k(0<k<\infty)$

and is confined between$g(r, 0)=$ $(r^{2}+1)/2r$ and$g(r, \infty)=2r/(r^{2}+1)$

:

$r \leq\frac{2r}{r^{2}+1}\leq g(r,k)\leq\frac{r^{2}+1}{2r}\leq\frac{1}{r}$ (8)

where $0\leq r\leq 1$ and the equalities of both ends hold only when$r=1$

.

The highest

and lowestvalues of$g(r, k)$

are

the arithmetic

mean

and the hannonic mean,

respectively, of$r$ and $1/r$

.

Thus,

even

for theextreme

case

($karrow 0$

or

$\infty$)the

compromiseline does notreach theboundary lines of the conflict regionunless $r$

$=1$,

as

virtually

no

cost(

$d_{R}=\Delta_{D}\underline{/karrow 0)}$

duetoitsabsolutedominanceincontrol$(karrow\infty)$

.

$\underline{fi}tnessW_{-}+B+\mapsto\gamma(- C- d_{D}).throu\underline{g}h$their relatedness $(r)$

.

Similarlv.

even

if$D$has

($karrow OI$

.

the cost

$d_{L}\underline{oaid}$

by$R$ (inthe efforts ofretaining$D$ for the altruistic service

relatedness $(r)$

.

This fact has

an

implication that demands

a

revision

ofHamilton’s

Rule and the InverseHamilton‘sRule,unless conflictcosts

are

allnegligible,

as we

see

inthefollowing.

First, for the

case

of

no

effective manipulation by $R(karrow 0)$, _{the threshold value}

of$B/C$ forthe altruistic behaviorto evolve for each value of$r$,

$\frac{B}{C}=g(r, 0)=\frac{r^{2}+1}{2r}$ (9)

is much lower than the

one

thatHamilton’s Rule predicts (Fig. 3). Forexample, when$r=1/2$ _and 1/4, _{respectively, Hamilton’sRule predicts that}$B/C$mustbe

2.0

and

4.0

forthe altruistic behaviorto evolve, whereas the

new

theory predicts that it

mustbe

more

than only

1.25

and 2.125. Orwhen$B/C$ is 2.0, Hamilton’s Rule

predicts that$r$mustbe

more

than 1/2 for the altruistic behaviorto evolve,whereas

the

new

theory predicts that it must be

more

than only

0.268.

For the

case

of

no

effectiveresistance by$R(karrow\infty)$, the threshold value of$B/C$

forthe altruistic behaviorto evolve is

$\frac{B}{C}=g(r, \infty)=\frac{2r}{r^{2}+1}$ (10)

This is muchhigherthan the$B/C$ ratiopredicted by the Inverse Hamilton‘s Rule

predicts (Fig. 3). _{Forexample,when} $r=1/4$ and 1/2,respectively, the Inverse Hamilton’sRule predicts that$B/C$must be only

0.25

and

0.5

for the altruistic

behaviorto evolve, whereas the

new

theoIy predicts that itmustbe

more

than

0.471

and

0.8.

Or when$B/C$is 0.5, theInverse Hamilton’s Rulepredicts that$r$

mustbe less than 1/2_{for the altruisticbehaviorto evolve, whereas the}

new

_theory predicts that itmust be less than

0.268.

Finally, the theory developed here indicates under what conditions

no

compromise is reached, and physical conflict

may

ensue.

Ingeneral, the

parameters $B,$ $C$,and$k$

are

not constant in specific conflict

scenes.

In such

a

case,

bothplayers $D$ and$R$ will evolveto adoptconditional strategies,depending

on

the

is

exactly correct,

a

compromise willbe reached,

as

derived above. If

one

of the

two incorrectlyestimates theparameters and ifboththink they

can

winthe conflict,

then the conflict will$actua\mathbb{I}y$ start. Specifically, when theparametervalues

are

close

to thecompromise line, then the judgment, whether tofight

or

not, _{will be difficult.}

Therefore,

we

can

say

thatthe closer the parametervalues

are

to the compromise

line (i.e., _{satisfyingthe critical condition} (4) _{for the evolution of}altmism), _the

more

likely it is that

no

compromisewillbe reached,and physical conflict will be actually

B

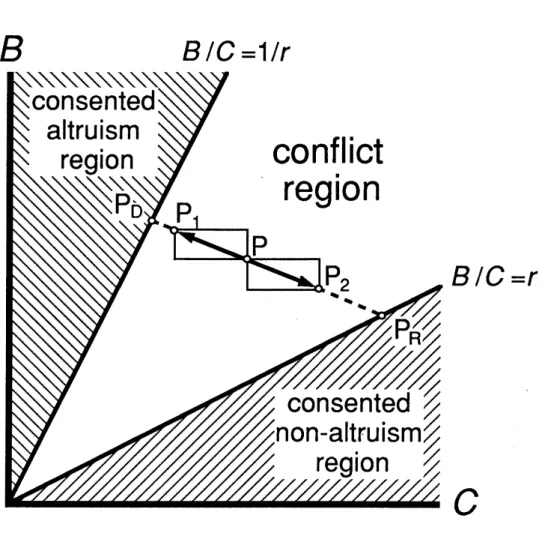
$B/C=1/r$

Fig. 1Threeregions in$(C, B)$-spacewith differentimplicationsfor theevolution ofanaltruistic behaviorof

donor(D)towardrecipient(R). Themiddle region definedbycondition(3)is the regionof conflict between$D$

andR. The outerregionsdefinedbyinequalities $B/C>1/r$_and$B/C<r$ are_{the regionsof}consensus_between$D$

and$R$:the$fo$–eris the$alm_{1}ism$region,wherein thesenseofevolutionarychoice,R”wants$D”$_,and$D$“is

willing”,totakethe$a$]$m_{1}istic$behavior,while thelatter isthenon-altmism region,where$D$”wants”,and$R” is$

willingto $pe itD’$,nottotakethe altruisticbehavior. Whenpoint$P(C, B)$fallsintheconflictregion,$D$and$R$

both wouldhave topaycosts if they pursuedthe conflict. Theconditionthat$D’s$inclusive fitnessvaluein the

caseof winningisgreaterthan it wouldbe in thecaseofavoidingthe conflict in the firstplace,givenas

inequality(4),can

oe

interpretedasbeingthat$Pl(C- kdR, B+dR)$,the pointobtainedbyshifting$P(C, B)$with

$P2$$obtainedbyshiftingP(C,B)withvector(kdR,- dR),isstilllocatedabovelineB/C=vector$($C+kdR,B$-dR),thepoint

($- kdR,$_dR),isstilll$\propto$$atedbelowlineB/C=l/r.ThesameconditionforR,givenasinequality(5),isthat$

$r$. As$dR$(theconflictcost)increases,the varying pointsPl andP2approachesthecritical lines$B/C=1/r$and

$B/C=r,$$respec\dot{0}vely$. IxtPDand$PR$,respectively, denote the$inters\infty tion\mu ints$thatPland P2meetwhen they

reachthose lines. Then,theconditionfor$D$tolose theconflictgamecan&statedthatPlreaches$PD$_,while P2

Fig.2 Summary of the results for conflict resolution in

the.

$(C, B)$-space. Line$B/C=g(r, k)$

divides theconflictregion intotwo sub-regions:theupperis the compromised altruism region, where$D$should withdraw ffom the conflict and take the$al\alpha uistic$behavior;and the lower is

the compromised non-altruism region, where$R$,onthecontrary,should withdrawffomthe

conflict and let$D$nottake the$altruis\dot{u}c$behavior. Notice that thislineconsistsof the

midpoints oftheline segments(withslope-l$/k$)definedbythe pairs ofintersectionpoints(PD andPR)indicated in Fig. 1. Theslopeofthe compromiseline,$g(r, k)$,decreasesas$k$increases

$(0\leq k\leq\cdot)$,andits rangeis confined betweentwobrokenlines(symmetrictoeach other with

respecttoline$B/C=g(r, 1)=1)$whoseslopesare $g(r, 0)=(r2+1)Qr$and$g(r, \cdot)=2r/(r2+$

$r$

Fig.3 The linesrepresentingthecritical conditions for the altruism evolution

representedasthe relations of$B/C$to$r$that Hamilton’s Rule predicts (thefirst

lme fromthetop),thenewtheory predicts for thecaseofnoeffective

manipulation by$R(kE0)$ (thesecond line fromthetop),itpredicts forthecase

ofnoeffectiveresistanceby$R(kE\cdot)$ (the second line from thebottom),and