Mathematical Analysis and Motion Control for Horizontal Bar Gymnastic Robot Hidekazu Kajiwara*1, Yukio Hashimoto*2, Toshihiko Matsuda*2 and Takeshi Ts

学 術 ・技 術 論 文

鉄 棒 ロボ ッ トの 数理 解 析 と運 動 制 御

梶

原

秀

一*1橋

本

幸

男*2松

田

敏

彦*2土

谷

武

士*3

Mathematical

Analysis

and

Motion

Control

for

Horizontal

Bar

Gymnastic

Robot

Hidekazu Kajiwara*1, Yukio Hashimoto*2, Toshihiko Matsuda*2 and Takeshi Tsuchiya*3

This paper discusses a motion control of horizontal bar gymnast robot with two links and one passive joint on the bar. First, we show that the amplitude of the swing of the first link increases with resonance and parametric exci-tation by swinging the second link periodically. Next, we propose the control method using entrainment to produce each excitation by swinging the second link •ein phase•f with the motion of the first link. In our method, the control input is consisted of periodic solution of van der Pol's equation inputted the angular velocity of the first link. Finally, we present experimental results that swing up control and continuous giant swings can be realized in the real robot.

Key Words: Gymnast Robot, Resonance, Parametric Excitation, Entrainment, Van der Pol's Equation

1.は じ め に メ カ ニ カ ル シ ス テ ム に 周 期 的 な 入 力 を 加 え る こ と に よ り,制 御 目 的 を達 成 で き る 場 合 が あ る.こ れ まで に 筆 者 ら は こ の よ う な シ ス テ ム と し て,皿 ま わ し や ブ ラ ン コ の 制 御 を 取 り上 げ て き た[1][2].文 献 国 で は 竿 の た わ み も考 慮 し た 数 理 モ デ ル に よ り,安 定 に 皿 を 回 す こ とが で き る タ イ ミ ン グが 存 在 す る こ と を 示 し,竿 の 固 有 周 期 以 上 で 竿 を 振 る だ け で,竿 を 振 る 周 期 と皿 の 回 転 周 期 が 同期 し,皿 まわ し が 実 現 で き る こ と を 明 らか に し た.文 献[2]で は ブ ラ ン コ を 大 域 的 に 制 御 で き る タ イ ミ ン グ と し て,ブ ラ ン コ の 振 れ と重 心 移 動 を1:2の 割 合 で 同 期 させ る と よ い こ と を 示 し,vander Pol方 程 式 に ブ ラ ン コ の 角 速 度 を 入 力 し,そ の 周 期 解 で 構 成 され る制 御 入 力 に よ りブ ラ ン コ の 振 れ を 制 御 す る 方 法 を提 案 し た.こ の よ うに,制 御 対 象 に タ イ ミ ン グ よ く周 期 的 な 入 力 を 加 え た と き,シ ス テ ム を う ま く制 御 で き る 場 合が あ る.本 研 究 で は,第1関 節 を 非 駆 動 と す る2リ ン ク の 鉄 棒 ロボ ッ トに お い て,非 駆 動 関 節 の 運 動 に 合 わ せ て タ イ ミン グ よ く駆 動 関 節 を 動 か す こ と に よ りそ の 運 動 を 制 御 で き る と考 え,鉄 棒 ロボ ッ トの 数 理 解 析 と 制 御 方 法 の 検 討 を行 っ た. 制 御 の デ モ ン ス トレ ー シ ョ ン や 器 械 体 操 に お け る 運 動 の 解 明 を 目 的 と し て,鉄 棒 ロ ボ ッ トが 研 究 され て き た.こ れ ま で に, 静 止 状 態 か ら の 振 り上 げ 倒 立 や1回 転 に い た る まで の 運 動 を 実 現 す る た め に 数 多 くの 制 御 方 法 が 提 案 され て い る[3]∼[6].従 来 の 研 究 で は こ の よ う な 運 動 を 実 現 す る た め に,全 体 の 運 動 を シ ミュ レ ー シ ョ ンで 確 認 し なが ら試 行 錯 誤 的 に 制 御 入 力 を 決 定 し て い た.そ の た め,実 際 に ロ ボ ッ トを 制 御 す る と き,パ ラ メー タ 同 定 誤 差 や 外 乱 な ど 影 響 に よ り制 御 誤 差 が 生 じ る と,そ の 運 動 が 制 御 で き な くな る場 合 が あ る.駆 動 関 節 を 制 御 す る タ イ ミ ン グ を 各 関 節 の 状 態 量 を も とに リア ル タ イム で 変 更 す る こ と で 上 記 の 問 題 は 解 決 で き る と考 え ら れ るが,こ の よ うな 制 御 方 法 は これ ま で 検 討 され て い な い.ま た,鉄 棒 ロボ ッ トを 動 作 させ る と き,ま ず 最 初 に 非 駆 動 関 節 で あ る 第1関 節 の 運 動 を励 起 す る 必 要 が あ るが,こ の 運 動 が 実 現 で き る 数 理 的 な メ カ ニ ズ ム に つ い て も あ ま り議 論 され て い な い よ うに 思 わ れ る . 本 論 文 で は まず,鉄 棒 ロ ボ ッ トに お い て 第2関 節 を 周 期 的 に 駆 動 し た と き,第1関 節 の 運 動 を 励 起 で き る タ イ ミン グ を シ ス テ ム の エ ネ ル ギ ー 変 化 率 か ら 解 析 す る.結 果 と し て,静 止 し た 状 態 か らの 振 り始 め で は 共 振 現 象,振 れ が 大 き くな っ た 場 合 は パ ラ メー タ 共 振 現 象 を 起 こ す タ イ ミ ン グ で 第2関 節 を 動 作 させ る こ と に よ り,効 率 よ く第1関 節 の 運 動 を励 起 で き る こ と を 示 す.そ の 後,上 記 の タ イ ミン グ で 第1関 節 と 第2関 節 を 同期 さ せ 続 け る た め に,vander Pol方 程 式 の 入 力 と し て 第1関 節 の 角 速 度 を 加 え,そ の 周 期 解 で 構 成 さ れ る 制 御 入 力 に よ り第2関 節 を 制 御 す る 方 法 を提 案 す る.実 際 に 鉄 棒 ロ ボ ッ トを 製 作 し 提 案 した 制 御 方 法 の 検 証 を行 っ た結 果,第1関 節 の 振 れ を 励 起 さ せ て 連 続 的 に ロボ ッ ト を 回 転 させ る 制 御 が 可 能 で あ っ た. 2.鉄 棒 ロ ボ ッ ト の モ デ ル と ダ イ ナ ミ ク ス 本 研 究 で は 鉄 棒 ロ ボ ッ ト を力 学 的 に 扱 うモ デ ル と し てFig.1 に 示 す よ うな2重 振 り子 を考 え る.こ の モ デ ル に お い てTable 1 原 稿 受付1998年4月3日 *1釧 路 工 業 高 等 専 門 学 校 *2室 蘭 工 業 大 学 *3北 海 道 大 学 大 学 院 工 学 研 究 科 *1Kushiro National C ollege of Technology *2Muroran Institute of Technology *3Graduate School of Engineering

, Hokkaido University

516 梶 原 秀 一 橋 本 幸 男 松 田 敏 彦 土 谷 武 士

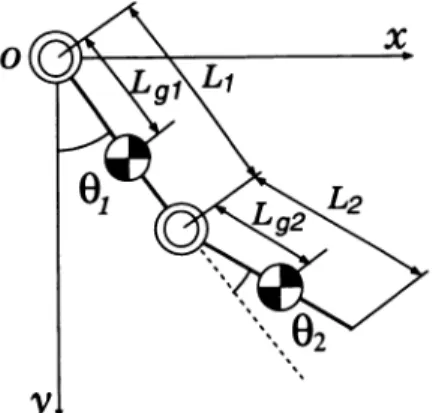
Fig. 1 Two-Link model of horizontal bar gymnastic robot

Table 1 Parameters of gymnastic robot

に 示 す 記 号 を 定 義 す る. 以 上 の 条 件 の も と に シ ス テ ム の 運 動 エ ネ ル ギ ーT,ポ テ ン シ ャル エ ネ ル ギ ー σ を 求 め る と 次 式 の よ う に 表 され る. 〓 +m2L1Lg2θ1(θ1+θ2)cosθ2(1) U=-(m1Lg1+m2L1)gCoSθ1 - m2Lg2gcos(θl+θ2)(2) J1=Jg1+m1L2g1+m2L21 J2=Jg2+m2L2g2 式(1)(2)を ラ グ ラ ン ジ ュ の 運 動 方 程 式 に 代 入 し て 鉄 棒 ロ ボ ッ トの 運 動 方 程 式 を 求 め る と次 式 と な る. Jθ+Dθ+P+G=τ(3) た だ し,

J=〓,D=〓,P=[P1P

2]

G=[G1G2],τ=[0 τ2],θ=[θ1θ2] J11=J1+J2+2m2L1Lg2cosθ2 J12=J2+m2L1Lg2cosθ2 J22=J2 P1=-m2L1Lg2θ2(θ2+2θ1)sinθ2 P2=m2L1Lg2θ21sinθ2 G1=(m1Lg1+m2L1)gsinθ1+m2Lg2gsin(θ1+θ2) G2=m2Lg2gsin(θl+θ2) 3.鉄 棒 ロ ボ ッ ト の 運 動 解 析 本 章 で は 鉄 棒 ロ ボ ッ トの 運 動 を 制 御 で き る タ イ ミン グ を 解 析 す る た め,鉄 棒 ロ ボ ッ トの 全 エ ネ ル ギ ー を 時 間 に つ い て 微 分 し た エ ネ ルギ ー 変 化 率 か ら解 析 す る. 鉄 棒 ロ ボ ッ トの 全 エ ネ ル ギ ー は 式(1)(2)よ り E=T+U(4) と な る.式(4)を 時 間 に つ い て 微 分 し,式(3)を 考 慮 し て 整 理 す る と 次 式 の エ ネル ギ ー 変 化 率 が 得 られ る. dE/dt= m2L1Lg2θ21θ2sinθ2+J2(θ1θ2+θ2θ2) +m2L1Lg2θ1θ2coSθ2-D1θ21 + m2Lg2gθ2sin(θ1+θ2)(5) 第2リ ン ク の 運 動 θ2を 時 間 的 に 変 化 させ た と きの エ ネ ル ギ ー 変 化 率 を 式(5)か ら求 め る た め に は,第1リ ン ク の 運 動 θ1の 運 動 を 式(3)か ら 求 め る 必 要が あ る.し か し,式(3)は 非 線 形 な 微 分 方 程 式 の た め 厳 密 に 解 を 求 め る こ とは 難 しい.そ こで, 以 下 で は 鉄 棒 ロ ボ ッ トの 運 動 状 態 に 適 応 し た 近 似 を導 入 す る こ とに よ り解 析 を 進 め る. (i)第1,第2リ ン ク の 運 動 が 微 小￨θ￨,￨θ2￨≪1な 場 合. 上 記 の 条 件 の も とで,あ る1周 期 中 の 第1リ ン クの 運 動 が θ1=αsin(ωt)(6) で 表 され る と き,第2リ ン ク を 第1リ ン ク と 同 期 さ せ て 次 式 の よ うに 動 か す 場 合 を 考 え る. θ2=βsin(ωt+φ)(7) こ の と き, sin(θ1+θ2)〓θ1+θ2(8) と 近 似 し て,式(6)(7)(8),お よび 式(6)(7)を 時 間 に つ い て 微 分 し た もの を 式(5)に 代 入 し,1周 期〓 に つ い て 平 均 を と る と,エ ネ ル ギ ー 変 化 率 の 平 均 は 次 式 と な る. <dE/dt>=〓[A1α βsin(2φ)+A2sinφ]-D1ω2/2α2

(9)

A1=m2L1Lg2ω2/4

A2=(J2+m2L1Lg2)ω2-m2Lg2g 上 式 よ り,鉄 棒 ロ ボ ッ トが 静 止 し た 状 態 か ら リ ン ク を 振 り出 す 場 合 は,第1リ ン ク の振 れ が 非 常 に小 さ い と し て A2≫A1α β(10) た だ し,A2>0と す る が 成 り立 つ と き,φ=〓 の と き,エ ネ ル ギ ー 変 化 率 が 最 大 に な る こ とが 分 か る. また,第2リ ン ク を動 か す 周 期 ω は 次 の よ う に し て 求 め ら れ る.

鉄 棒 ロボ ッ トの 運 動 方 程 式(3)を リ ン ク の 振 れ 角 θ1,θ2が 微 小 で あ る と し て 線 形 近 似 す る と次 式 と な る. θ1+2γ θ1+ω2kθ1=B1θ2-B2θ2(11) た だ し, JJ=J1+J2+2m2L1Lg2 ω κ=〓 B1=〓,B2=〓 式(6)(7),な ら び に そ れ ら を 時 間 に つ い て 微 分 し た も の を 鉄 棒 ロ ボ ッ トの 運 動 方 程 式(11)に 代 入 し て 整 理 す る と,位 相 φ に つ い て 次 の 関 係 を 得 る. tanφ=2γω/ω2k-ω2(12) 上 式 よ り,φ=2/〓 で 第1リ ン ク と第2リ ン ク を 同 期 させ る と き,そ の 周 期 ω は ω〓 ωκ(13) と な る.し た が っ て,静 止 し た 状 態 か ら 鉄 棒 ロ ボ ッ トを 動 作 さ せ る 場 合,そ の 固 有 周 期 で 第2リ ン ク を 動 か す こ と に よ り,共 振 現 象 を 利 用 し て 第1リ ン ク の 振 れ を励 振 さ せ る と よ い こ とが 分 か る. (ii)振 れ が 増 加 し て￨θ1￨≫￨θ2￨と な っ た 場 合. た だ し,￨θ2￨≪1と す る. こ こで は,振 れ が 増 加 し て 第1リ ン ク の 振 れ が 第2リ ン ク に 比 べ て 非 常 に 大 き くな っ た 場 合 を 考 え る. こ の と き2リ ン ク の 鉄 棒 ロ ボ ッ トの 運 動 をFig.2に 示 す よ う に,鉄 棒 ロボ ッ トの す べ て の 質 量 が 重 心Gに 集 中 し た1リ ン クの 振 り子 の 運 動 と して 近 似 す る. よ っ て,1周 期 中 の 振 り子 の 運 動 が 次 式 で 表 さ れ る とす る と θ1=-g/〓sinθ1(14)

硲 は 重心 の平均 位置

こ の と き,振 り子 の 運 動 は 周 期Tが 〓〓(15) k=sinθmax/ 2 θ=0の と き θ=θmax で 表 され る 周 期 関 数 と な るか ら,振 り子 の 運 動 は θ1=Σ∝n=1αnsin(nωt)(16) ω=2〓/T と で き る. 以 上 の 条 件 の も と で,さ ら に sin(θ1+θ2)〓sinθ1(17) と 近 似 で き る と す る と,式(3)よ り 次 式 の 関 係 が 得 ら れ る. gsinθ1=-N1/M1θ1-N2/M1θ2 +N3/M1θ1θ2θ2+N4/M1θ2θ22(18) M1=m1Lg1+m2L1+m2Lg2 Nl=J1+J2+2m2L1Lg2 N2=J2-m2L1Lg2 N3=2m2L1Lg2θ1θ2θ2 N4=m2L1Lg2 式(7)(16)(18)を 式(17)を 利 用 し て 近 似 し た エ ネ ル ギ ー 変 化 率 の 式 に 代 入 し,1周 期Tに わ た っ て 平 均 を と る と 次 式 と な る. < dE/ dt>=〓 一D1α21ω2/2(19)〓 〓第1リ ン クの 振 幅 が 大 き く α1β≫B2/B1(20) が 成 り立 つ と き,φ=〓 の と きエ ネ ル ギ ー 変 化 率 が 最 大 に な る こ とが 分 か る. い ま,支 点 か ら重 心Gま で の 距 離LGは LG=〓

•¬ Fig. 2 One-link model of gymnastic robot

518 梶 原 秀 一 橋 本 幸 男 松 田 敏 彦 土 谷 武士 と な る か ら(付 録A参 照),￨θ2￨≪1の 場 合, LG=〓-〓( 22 )と 展 開 で き る,し た が っ て,第1リ ン ク と 第2リ ン クが 位 相 差 φ=〓/4の 関 係 を 保 ち な が ら 同 期 し て い る と き, B2=βsin(ωt+〓/4)(23) 上 式 を 式(22)に 代 入 し て 整 理 す る と LG=lg-σsin(2ωt)(24 )た だ し,lg=〓-〓 δ=〓と な る.以 上 の こ と か ら,鉄 棒 ロボ ッ トの 第1リ ン ク と 第2リ ン クが4の 位 相 関 係 で 運 動 し て い る と き,そ の 等 価 的 な 単 振 り子 の 運 動 を 考 え る と,振 り子 の 振 れ と重 心 の 上 下 運 動 が1:2 の 割 合 で 同 期 して い る こ と に 相 当 し,ブ ラ ン コ の 振 れ を 励 起 さ せ る場 合 と 等 価 で あ る こ とが 分 か る[3].し た が っ て,第1リ ン ク の振 れ が 第2リ ン クの 振 れ よ り も 大 き く な っ た 場 合 は,パ ラ メー タ共 振 現 象 を利 用 し て 第1リ ン クの 振 れ を 励 起 す る と よ い こ とが 分 か る. 4.引 き 込 み を 利 用 し た 鉄 棒 ロ ボ ッ ト の 運 動 制 御 前 章 で は,鉄 棒 ロボ ッ トの 第1リ ン クの 振 れ が 微 小 な 場 合 と 大 き くな っ た 場 合 に 分 け て,第1リ ン クの 振 れ を 励 起 で き る タ イ ミン グ を解 析 し た,そ の 結 果,そ れ ぞ れ の 場 合 で は 第1リ ン ク と第2リ ン ク を 同期 さ せ る 位 相 差 が 異 な る こ と を 明 らか に し た.本 章 で は,非 線 形 振 動 子 の 引 き込 み 現 象 を利 用 し て,各 リ ン ク を を 同 期 させ る 方 法 に つ い て 述 べ る.

非 線 形 振 動 子 と し てvan der Pol方 程 式,そ の 入 力 と し て 鉄 棒 ロボ ッ トの 第1リ ン クの 角 速 度 を加 え た も の を 考 え る.

x-ε(1-x2)x+ω2xx=kθ1(25)

鉄 棒 ロ ボ ッ トの 第1リ ン クが 式(16)で 運 動 し て い る と き, ωx〓ω,ま た はKが 十 分 大 き い と き,van der Pol方 程 式 の

周 期 解 と θ1が 同 期 す る[3]. こ の と き,方 程 式 に 与 え る 初 期 値 を 適 当 に 調 整 す る と,そ の 周 期 解 は 次 式 と な る. x=〓sin(ωt)(〓>0)(26) し たが っ て,鉄 棒 ロボ ッ トの 振 り始 め は 第2リ ン ク を 方 程 式 の 解 を 利 用 し て θ2=Ex(E>0)(27) と す る こ と に よ り,第1リ ン ク と第2リ ン ク の 位 相 差 を〓 と で き る.

また,第1リ

ン クの振 れが 大 き くな った場 合は

θ2=E{cos(〓)AG1x+sin(〓)AG2x}(28)

AG1,AG2はx,xの 振 幅 を1に す る 変 数 とす る こ と に よ り,第1リ ン ク と 第2リ ン クの 位 相 差 をnaと で き る. 5.実 験 本 章 で は 前 章 で 示 し た 鉄 棒 ロボ ッ トの 制 御 方 法 の 有 効 性 を 確 認 す る た め に,実 際 に ロボ ッ トを 製 作 し実 験 を 行 っ た 結 果 に つ い て 述 べ る. 5.1鉄 棒 ロ ボ ッ トの 構 成 Fig.3に 製 作 し た 鉄 棒 ロ ボ ッ ト,Table2に ロボ ッ トの 各 パ ラ メ ー タ を 示 す. ロ ボ ッ トの 第2関 節 部 に ラ ジ コ ン 用 の サ ー ボ モ ー タが 取 り 付 け て あ り,こ の モ ー タ が 回 転 す る こ と に よ り第2リ ン ク を 動 か す こ とが で き る.制 御 器 に は 富 士 通 社 製FM/V-BIBLO-NP13(OS-Linux)を 使 用 し,制 御 プ ロセ ス はC言 語 で 記 述,制 御 周 期 は20[msec]で 行 っ た.制 御 器 の 出 力 は 制 御 器 の パ ラ レ ル ポ ー トか ら出 力 され モ ー タ を 駆 動 す る.第1関 節 の 角 速 度 は 第2関 節 の モ ー タ部 に 取 り付 け ら れ た 圧 電 ジ ャ イ ロ セ ンサ(村 田 製 作 所 製ENC-05S)の 出 力 をA/D変 換 しパ ラ レ ル ポ ー トか ら 制 御 器 に 取 り込 ん で い る.ま た,vander Pol方 程 式 の 解 は 制 御 周 期 ご と に4次 のRunge-Kutta-Gill法 に よ り計 算 し た. こ の と き,方 程 式 に 与 え た 初 期 値 は(x,x)=(0.01,0)で あ り, 使 用 した 方 程 式 の 各 パ ラ メ ー タ は(K,ε,ωk)=(8,1.3,8.1)で あ る. 5.2実 験 結 果 鉄 棒 ロ ボ ッ トの 運 動 の 様 子 を8ミ リ ビ デ オ カ メ ラ で 撮 影 し, 1/30[sec]ご との 振 れ の 角 度 を計 算 し て,グ ラ フ に プ ロ ッ トし た 結 果 をFig.4(a)∼(c)に 示 す.

Fig. 3 Horizontal bar gymnastic robot

Fig.4(a)は 第1リ ン ク と 第2リ ン ク の 位 相 差 を φ=〓/2 , Fig.4(b)は 位 相 差 を φ=〓 で 同 期 さ せ た 場 合 で あ る.第3 章 の 解 析 で 示 し た よ う に,第1リ ン クの 振 れ が 小 さ い 場 合 は φ=〓 振 れ が 大 き くな っ た と きは,φ=〓 の 方 が 振 幅 の 増 加 率 が 大 きい こ とが 分 か る.ま た,Fig.4(a)よ り第1リ ン クの 運 動 は 定 常 に 達 し,振 幅 が ほ とん ど増 加 し な くな る こ とが 分 か る. こ れ は エ ネ ル ギ ー 変 化 率 式(19)よ り,第1リ ン ク の 振 れ が 増 加 し た 場 合,左 辺 第2項 の 損 失 エ ネ ル ギ ー の 項 が 大 き くな り <dE/ dt>=0(29) と な る た め で あ る と考 え ら れ る.第2リ ン クの 振 幅 を 増 加 させ る と,ロ ボ ッ トを 回転 させ る こ と は 可 能 で あ る が,振 れ が 大 き くな っ た と きの エ ネ ル ギ ー 増 加 率 が 小 さ い た め,回 転 を 始 め る と き に 勢 い を つ け る こ とが で きず,連 続 的 に 回 転 で き な い.し か し,φ=〓 の 場 合 は,180ﾟ付 近 で エ ネ ル ギ ー 増 加 率 が 非 常 に 大 き い た め,加 速 し て 回 転 運 動 に 入 る こ とが で き,連 続 で6 ∼8回 の 大 車 輪 を 実 現 す る こ とが で き た . Fig.4(c)は 位 相 差〓 で 振 れ を増 加 させ て い る と き,第1リ ン ク と 第2リ ン クの 同 期 を くず す た め に 外 乱 を 加 え た 場 合 で あ る.外 乱 を加 え ら れ て も再 び 同 期 し,振 れ が 増 加 して い くこ と が 分 か る. 6.お わ り に 本 論 文 で は 鉄 棒 ロボ ッ トの 振 れ を 励 起 で き る タ イ ミン グ と し て,振 り始 め は 共 振 現 象,振 れ が 大 き くな っ た 場 合 に は,パ ラ メー タ 共 振 現 象 を 利 用 して 振 れ を 励 振 させ る と よ い こ と を 明 ら か に し た.さ ら に,非 線 形 振 動 子 の 引 き込 み 現 象 を 利 用 し て, 第1リ ン ク と 第2リ ン ク を 同 期 させ て 制 御 す る 方 法 を提 案 し た. 本 手 法 で は 第1リ ン クの お お よ そ の 周 期 と角 速 度 だ け が 分 か れ ば よ く,非 常 に 簡 単 な 制 御 則 で 鉄 棒 ロ ボ ッ トで 大 車 輪 を 実 現 す る こ とが で き る.今 後 は,3リ ン ク以 上 の 鉄 棒 ロ ボ ッ トに も本 研 究 の 手 法 を 適 用 し た い と 考 え て い る. 付 録A.式(21)の 導 出 Fig.1に お い て,原 点Oか ら各 リ ン ク の 重 心 へ の 位 置 ベ ク ト ル をr1=[x1,y1]T,r2=[x2,y2]Tと し,Fig.2に お い て,す べ て の 質 量 が 重 心Gに _{集 中 し て い る とす る と,そ の 位 置ベ ク} トルTG=[xG,yG]Tは rG=m1r1+m2r2/m1+m2(30) と定 義 で き る[7]. 上 式 よ り,重 心Gへ の 位 置 ベ ク トルTGの 各 成 分 は xG=m1x1+m2x2/ m1+m2

(31)

y G=m1y1+m2y2/m1+m2 と な り,Fig.2に お け る 重 心 ま で の 距 離LGは LC=〓(32) と な る. Fig.1に お い て 各 リ ン ク の 重 心 へ の 位 置 ベ ク ト ル の 成 分 は Fig. 4 Swingup control of gymnastic robot

520 梶 原 秀 一 僑 本 幸 男 松 田 敏 彦 土 谷 武 士 x1=Lg1sinθ1(33) y1=Lg1cosθ1 x2=L1sinθ1+Lg2sin(θ1+θ2)(34) y2=L1COSθ1+Lg2cOS(θ1+θ2) と な る か ら,式(31)(33)(34)を 式(32)に 代 入 し て 整 理 す る と 式(21)が 導 出 で き る, 参 考 文 献 [1] 梶 原 他:“ 皿 まわ しの 数 理 とロ ボ ッ トに よ る実 現 ”,日 本 ロボ ッ ト学 会 誌,vol.16, no.4, pp.483-490, 1998. [2] 梶 原 他:“ 引 き 込 み を 利 用 し た ブ ラ ン コ の 振 れ 制 御 ”,日 本 ロ ボ ッ ト 学 会 誌,vol.17, no.4, pp.520-525, 1999. [3] 林 他:“ 二 重 物 理 振 り 子 の 制 御 ”,日 本 機 械 学 会 論 文 集(C),vol.56, no.522, pp.175-178, 1990. [4] 高 嶋 俊:“ 鉄 棒 運 動 ロ ボ ッ ト の 制 御 ”,第8回 日 本 ロ ボ ッ ト 学 会 学 術 講 演 会 予 稿 集,pp.619-620, 1990. [5] 小 島 他:“ 非 駆 動 関 節 を 有 す る2関 節 形 鉄 棒 ロ ボ ッ ト に 関 す る 研 究 ”, 日 本 機 械 学 会 論 文 集(C), vol.57, no.539, pp.125-130, 1991. [6] 橋 本 他:“ 鉄 棒 ロ ボ ッ トの 運 動 制 御 ”,日 本 機 械 学 会 ロ ボ テ ィ ク ス ・ メ カ ト ロ ニ ク ス 講 演 会'92講演 論 文 集(Vol.A), pp.45-50, 1992. [7] 原 島 鮮:力 学.p.157,裳 華 房,1958. 梶 原 秀 一(Hidekazu Kajiwara) 1971年1月25日 生.1995年 室 蘭 工 業大 学 博 士 前 期 課 程 電 気 電 子 工 学 専 攻 修 了.現 在 釧 路 工 業 高 等 専 門学 校 電 子工 学 科助 手.制 御 工 学,ロ ボ ッ ト工 学 の研 究 に 従事,計 測 自動 制 御学 会 の 会 員. (日 本 ロボ ッ ト学 会正 会員) 松 田 敏 彦(Toshihiko Matsuda) 1934年1月20日 生,1956年 室 蘭工 業 大 学 電 気工 学科 卒 業.北 海 道 大学 工学 部 助 手,室 蘭 工 業大 学講 師,助 教 授 を経 て1978年 同大 学電 気 工 学 科 教 授. 現 在 同 大 学 電 気 電 子 工 学 科 教 授.工 学博 士,電 気 機 器,電 動 機 制 御 に 関 す る 研 究 に 従 事.電 気学 会 の 会 員. 橋 本 幸 男(Yukio Hashimoto) 1953年3月8日 生.1979年 室 蘭工 業 大学 大 学 院修 士 課程 電子 工学 専 攻修 了.高 校 の 非常 勤 講 師等 を経 て1983年 室 蘭工 業 大学 電子 工 学科 助手.1990年 よ り同大 学電 気 電 子工 学 科助 手,現 在 助教 授.制 御工 学,メ カ トロニ ク スの研 究 に従 事.工 学博 士,計 測 自動制 御 学 会の 会 員.(日 本 ロボ ッ ト学 会正 会 員) 土 谷 武 士(Takeshi Tsuchiya) 1941年2月2日 生.1965年 北 海 道 大 学 大 学 院 修 士 課 程 電 気 工 学 専 攻 修 了.1966年 同 大 学 工 学 部 電 気 工 学 科 講 師,1983年 同 教 授,1997年 よ り 同 大 学 大 学 院 工 学 研 究 科 教 授.制 御 工 学,ロ ボ ッ ト工 学, パ ワ ー エ レ ク ト ロ ニ ク ス な ど の 研 究 に 従 事.工 学 博 士.計 測 自 動 制 御 学 会,シ ス テ ム 制 御 情 報 学 会, 日本 機 械 学 会,電 気 学 会,日 本 フ ァ ジ ィ学 会,IEEEの 会 員. (日 本 ロ ボ ッ ト学 会 正 会 員)