論文
ガ ウ ス 関 数 に 基 づ くFree-Form
Deformation*
-対話的なモ デル
変形のための基礎理論-吉
田
典
正**.加
納
顕
也***北
嶋
克
寛**
Free-Form Deformations Based on Gaussian Functions
- Fundamental Theory for Interactive
Modeling-Norimasa YOSHIDA, Ken'ya KANOU and Katsuhiro KITAJIMA
Interactive and intuitive modeling is one of the most important issues in geometric modeling. However, modeling a
complex object interactively and intuitively is still a difficult problem. In this paper, new Free-Form Deformations (FFDs)
based on Gaussian functions are introduced. Different from previous FFDs that are based on Bernstein or B-spline
functions, FFDs based on Gaussian functions allow an arbitrary number of control points to be placed in arbitrary positions.
Moreover, the standard deviations of Gaussian functions can control the localness of the effects of control points. These
facts provide designers with more interactivity and more intuitiveness. The designer can place a manipulation point in the
region to be modified, and by changing the standard deviations, the designers can choose the effect of localness of the
movement of the manipulation point. The definition of FFDs based on Gaussian functions, as well as several examples of
the FFDs, is presented.
Key words: geometric modeling, free-form deformation, direct manipulation, Gaussian functions
1.緒 言 対 話 的 か つ 直 感 的 に モ デ リ ン グ を す る こ と の で き る 手 法 は, 長 く望 ま れ て い る.し か し な が ら,複 雑 な 形 状 を 対 話 的 か つ 直 感 的 に 作 成 す る こ と は,依 然 と して 困 難 な 問 題 で あ る.ス プ ラ イ ン曲 面 の 制 御 点 の 位 置 を 変 更 す る 方 法 は 一 般 に 用 い ら れ て い る が,曲 面 が 非 常 に 多 く の 制 御 点 で 構 成 さ れ 曲 面 全 体 を 変 形 す る場 合 に は,多 数 の 制 御 点 を 操 作 し な く て は な ら な い. Free-FormDeformation(FFD)は,物 体 の 埋 め 込 ま れ て い る 空 間 を 変 形 す る こ と に よ っ て 物 体 を 変 形 す る ツ ー ル で あ る. FFDは,形 状 モ デ ル に 独 立 な 変 形 手 法 で あ る の で,ス プ ラ イ ン曲 面1ポ リ ゴ ン 曲 面,陰 関 数 曲 面 な ど 任 意 の 曲 面 を 変 形 す る こ とが で き る.ま た,空 間 の 変 形 を 定 義 す る 格 子 点 の 数 は, 変 形 さ れ る 物 体 に 独 立 で あ る の で,ス プ ラ イ ン 曲 面 の よ う に 多 く の 制 御 点 を 変 更 す る 必 要 は な い.し か しな が ら,FFDは, 空 間 の 変 形 を 定 義 す る 格 子 の 形 状 に 制 限 が 設 け られ て い る 等 の 問 題 点 を もつ. 本 研 究 で は,任 意 個 の 格 子 点 を任 意 の 位 置 に 配 置 す る こ と が で き,移 動 す る 格 子 点 の 変 形 へ の 影 響 度 を 変 え る こ と が で き るFFDを 提 案 す る.本 研 究 で は,任 意 の 位 置 の 点 を 移 動 さ せ る た め に 操 作 点 を 設 け,操 作 点 か ら格 子 点 を 自動 的 に 算 出 し,操 作 点 の 移 動 か ら格 子 点 の 移 動 を 計 算 し空 間 を 変 形 す る こ と に よ っ て 物 体 の 変 形 を行 う.操 作 点 を 任 意 の 位 置 に 配 置 す る こ と が で き る の で,操 作 点 を モ デ ル 上 に 置 い て 直 接 変 形 さ せ る こ と も 可 能 で あ る.ま た,ガ ウ ス 関 数 の 標 準 偏 差 を 変 え る こ と に よ っ て,移 動 さ せ る 操 作 点 の 変 形 へ の 影 響 度 を 変 え る こ と が で き,同 じ移 動 で モ デ ル の 局 所 的 な 変 形 も グ ロ ー バ ル な 変 形 も 可 能 で あ る.本 論 文 で は,こ の よ う な 自 由 な 変 形 を 行 う こ と の で き る 新 し いFFDの 手 法 を 述 べ る. 2.Free-FormDeformation Free-FormDeformation(FFD)1)2)5)∼8)は,変 形 す る 形 状 モ デ ル ま た は モ デ ル の 一 部 を 空 間 に埋 め 込 み,空 間 を 変 形 す る こ と に よ っ て モ デ ル を 変 形 す る 手 法 で あ る.空 間 の 変 形 は,図 1に 宗 す よ う に 平 行 六 面 体 形 式 に配 置 され た 格 子 点(制 御 点) を移 動 す る こ と に よ っ て 実 現 さ れ る.一 般 に,変 形 さ れ る モ デ ル は,格 子 内 に 置 か れ る. FFDは,R3か らR3へ の 非 線 形 写 像 と して 定 義 され る.グ ロ ー バ ル 座 標 系 に お け る 点 の 座 標 をs ,t,u局 所 座 標 系 に 変 換 し,局 所 座 標 系 に お い て 座 標(s,t,u)で あ る 点 は,次 式 に よ っ てP(s,t,u)へ と 変 換 され る. 〓(1) た だ しBi(x)はBernstein関 数 ま た はB-spline関 数 で あ り,
Fig. 1 A parallelpipedical lattice
*原 稿 受 付 平 成11年1月8日
**正 会 員 東 京 農 工 大 学(東 京 都 小 金 井 市 中 町2-24-16) ***エ ム ズ フ ァ ク ト リー(東 京 都 品 川 区 西 五 反 田1-7-6 ,トミエビル5F)
吉 田 ・加 納 ・北 嶋:が ウ ス 関 数 に 基 づ くFree-FOrmDeformation Vijkはs,t,u方 向 にi,j,k番 目 の 制 御 点 で あ る.な お,理 論 的 にFFDは,Rnか らRnへ の 写 像 に容 易 に 拡 張 す る こ と が で き る. FFDは,最 初Bernstein関 数 に 基 づ く も の がSederbergら に よ っ て 提 案 さ れ た8).そ の 後,Griessmairら は3変 数 の B-sphne関 数 に 基 づ くFFD5)を,Davisら は 有 理Bernstein 関 数 に 基 づ くFFD2)を,Lamousinら はNURBS関 数 に 基 づ くFFD7)を 提 案 して い る.こ れ ら は,そ れ ぞ れ 特 徴 を も っ が, いず れ も 格 子 が 平 行 六 面 体 形 状 に 制 約 さ れ る.
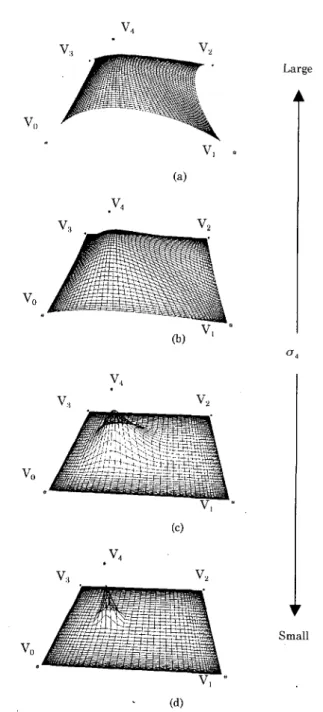
Coquillartら は,任 意 に 配 置 さ れ た 格 子 でFFDを 行 う 手 法 (EFFD,Extended Free-Form Deformation)を 提 案 して い る1). 任 意 の 格 子 は チ ャ ン ク(chunk)の 組 み 合 わ せ と して 表 現 さ れ,各 チ ャ ン ク ご と にFFDが 適 用 さ れ る.EFFDで は,チ ャ ン ク 間 の 連 続 性 が 保 た れ,チ ャ ン ク の 端 点 と チ ャ ン ク の コ ー ナ の 接 線 を 変 更 す る こ と に よ っ て 変 形 が 実 現 され る. Hsuら は,埋 め 込 ま れ て い る 物 体 上 の 点 を 直 接 操 作 す る こ と に よ っ て,FFDを 制 御 す る手 法 を 提 案 して い る6). Coquillartら はFFDを 任 意 の 格 子 に拡 張 し,Hsuら は 直 接 変 形 が 可 能 な よ う にFFDを 拡 張 し た.し か し な が ら,い ず れ もFFDを 拡 張 す る た め に 数 値 計 算 あ る い は 疑 似 逆 行 列 と い う特 別 な 処 理 を 必 要 と し て い る.特 別 な 処 理 を 行 う こ と な く, 任 意 の 格 子 に 対 応 で き,直 接 変 形 が 可 能 なFFDが 望 まれ る. 3.有 理 ガ ウ ス 曲 線 ・曲 面 ガ ウ ス 関 数 に 基 づ くFFDは,有 理 ガ ウ ス 曲 線 ・曲 面4)を 基 礎 と し て い る.こ こ で は,有 理 ガ ウ ス 曲 線 ・曲 面 に つ い て 述 べ る.有 理 ガウ ス 曲 線 ・曲 面 は ,Ghostasbyに よ っ て 提 案 さ れ,密 で 雑 音 の あ る 点 集 合 か ら構 造 を 復 元 す る た め に 構 築 さ れ た3).有 理 ガ ウ ス 曲 線 ・曲 面 式 は.B-spline関 数 を ガ ウス 関 数 に 置 き 換 え たNURBSの 式 と 似 て い るが,次 の 点 で 異 な っ て い る.、 (1)生 成 さ れ る 形 状 の 曲 率 値 を 制 御 す る 自 由 変 数 と し て ガ ウ ス 関 数 の 標 準 偏 差 を用 い る. (2)任 意 個 の 制 御 点 を任 意 に 配 置 す る こ とが で き る. こ こで は,例 と し て 有 理 ガ ウ ス 曲 面 に つ い て 述 べ る.有 理 ガ ウ ス 曲 線 も 同 様 に 定 義 さ れ る.制 御 点 ベ ク トルV,(i=l ,…n) で 構 成 され る 有 理 ガ ウ ス 曲 面 は, 〓 (2) で 定 義 さ れ る.こ こ に, 〓(3) は,曲 線 の1番 目 の 基 底 関 数 で,wiはi番 目 の 制 御 点 の ウ ェ イ トで あ る. 〓(4) は,(si,ti)を 中 心 とす る 標 準 偏 差 σi,高 さ1の ガ ウ ス 関 数 で あ る.ガ ウ ス 曲 面 は,NURBS曲 面 な ど と 同 様 に 凸 閉包 性 が 成 り立 つ が,標 準 偏 差 の 値 を 変 え る こ と に よ っ て 基 底 蘭 数 の 値 を 変 え る こ と が で き る.す な わ ち,ガ ウ ス 関 数 の 標 準 偏 差 に よ っ て,曲 面 形 状 に 対 す る 制 御 点 の 局 所 性 の 度 合 い を 制 御 ず る こ と が 可 能 と な る.σiの 値 が 小 さ く な る とi番 目 の 基 底 関 数 が よ り局 所 的 に 中 心 的 に な り,曲 面 に 対 す るViの 影 響 が 大 き くな る.従 っ て,Viを 移 動 させ る と,そ の 近 傍 の 曲 面 形 状 に も っ と も 大 き く 影 響 す る.σiの 値 が 大 き くな る と ,Viの 影 響 は 広 い 範 囲 に わ た り,Viを 動 か した と き に そ の 影 響 範 囲 は 広 い 範 囲 に わ た る も の と な る.ガ ウ ス 関 数 の 標 準 偏 差 が 小 さ い場 合,有 理 ガ ウ ス 曲 面 は 制 御 点 の 近 傍 を 通 る よ う に な り, 局 所 的 な 詳 細 さ を 保 持 す る.一 方,ガ ウ ス 関 数 の 標 準 偏 差 が 大 き い 場 合 に は,曲 面 は よ り小 さな 曲 率 を もつ よ う に な り, 形 状 の 全 体 的 な 特 徴 を と らえ る よ う に な る.ウ ェ イ トwiは, NURBSに お け るそ れ と 同 じ意 味 を も つ.す な わ ち,wiを 大 き くす る と 曲 面 は 制 御 点 の 近 く に 引 っ 張 ら れ,小 さ く な る と 離 れ て い く. 図2に 標 準 偏 差 を 変 え た ガ ウ ス 曲 面 を 示 す.V0,V1,V2 , V3,V4は,曲 面 を 定 義 す る 制 御 点 で あ り,各 点 の ウ ェイ トは 1と し て い る 。 図2(a)に お い て す べ て の 標 準 偏 差 は 同 じ 値 で あ る が,(b),(c),(d)で はV4の 標 準 偏 差 だ け を こ の 順 で 小 さ く し た.
Fig. 2 Gaussian surfaces with different standard deviations
吉田 ・加 納 ・北 嶋:が ウ ス 関 数 に 基 づ くFree-FormOeformation 有 理 ガ ウ ス 曲 線 ・曲 面 で は,理 論 的 に,制 御 点 は 曲 線 ・曲 面 全 体 に影 響 す る.す な わ ち,曲 線 ・曲 面 全 体 を 描 く た め に, す べ て の 制 御 点 を 用 い る 必 要 が あ る.し か しな が ら,ガ ウ ス 関 数 は 中 心 か ら離 れ る と指 数 関 数 的 に0に 近 づ く の で,実 際 の 計 算 で は 一 部 の 制 御 点 だ け を 用 い れ ば よ い.計 算 に 要 求 さ れ る 正 確 さ を εと し,ガ ウ ス 関 数 の 標 準 偏 差 を0と す る と き, パ ラ メ ー タs0で の 点 の 座 標 を 計 算 す る た め に は,式(5)の 範 囲 に あ る ノ ー ドの 制 御 点 だ け を 利 用 す れ ば よ い4)5). 〓(5) 以 上 に 述 べ た よ う に,有 理 ガ ウ ス 曲 線 ・曲 面 は,標 準 偏 差 の 値 を 変 え る こ と に よ っ て 同 じ 制 御 点 で 曲 面 の 形 を 変 更 す る こ と が で き,NURBSやB ・zier曲 面 な ど と異 な り任 意 個 の 制 御 点 を 任 意 に 配 置 で き る. 4.ガ ウ ス 関 数 に 基 づ くFFD 物 体 の 定 義 さ れ て い る 座 標 系 を 鋤 と し,ガ ウ ス 関 数 に 基 づ くFFDを, 〓(6) と 定 義 す る.こ こで, 〓(7) は,i番 目の 基 底 関 数 で あ り, 〓(8) は,(si,ti,ui)を 中 心 と す る 高 さ1の ガ ウ ス 関 数 で あ る, σi,s,σ,i,t,σ,i,uは,各 軸 方 向 のi番 目 の ガ ウ ス 関 数 の 標 準 偏 差 で あ る.こ の よ う に,各 軸 方 向 に 標 準 偏 差 を 設 け る こ と に よ っ て, 各 制 御 点 の 影 響 の 範 囲 を 軸 方 向 ご と に 変 え る こ とが 可 能 と な る 。 標 準 偏 差 は,パ ラ メ ー タs,t,uと 同 じ ス ケ ー ル で あ る 必 要 が あ る.ガ ウス 関 数 に 基 づ くFFDで は,任 意 個 の 制 御 点 を 任 意 に配 置 す る こ と が で き る が,一 般 の 位 置 に あ る4点 を 含 ま な く て は な ら な い.式(6)に み る よ う に,ガ ウ ス 関 数 に よ る FFDは,制 御 点 ベ ク トル の 線 形 結 合 と して 表 現 さ れ る の で, 制 御 点 ベ ク トル が 空 間 を 張 らな い 場 合 に は,FFDを 行 っ た 形 状 が 平 面 や 線 に含 ま れ る 形 状 に 縮 退 し て しま う. 式(6)は,ガ ウ ス 関 数 に 基 づ くFFDを 定 義 す る が,NURBS やB ・zierと 同 様 に 制 御 点 と 曲 面 上 の 点 が 離 れ て お り、 対 応 関 係 が 理 解 しに く い.そ こ で,逆 変 換11)に よ っ て,指 定 した 点 (操 作 点)を 通 過 す る よ うな 制 御 点 を 求 め る.鷺 個 の 操 作 点 .ベ ク トル をP,(i=1,…n)と し,Piの 座 標 を(si,ti,ui)とす る と,
〓(9) と い う 式 を 立 て る こ と が で き る.式(9)を 解 く こ と に よ っ て 制 御 点 ベ ク トルViが 求 ま り,任 意 の 座 標(s,t,u)を 式(6)に よ っ て 変 換 す る こ とが で き る.式(9)及 び 式(6)を 用 い る こ と に よ っ て, 変 形 した い 任 意 の 点 に 操 作 点 を お き,操 作 点 を 移 動 さ せ る か 標 準 偏 差 を 変 更 す る こ と に よ っ て,モ デ ル を 変 形 す る こ と が で き る.' 図3に,ガ ウ ス 関 数 に 基 づ くFFDの 流 れ を 示 す.ま ず,操 作 点 を 配 置 し,操 作 点 の 移 動 また は 標 準 偏 差 の 変 更 を 行 う.
Fig. 3 Flow of FFDs based on Gaussian functions
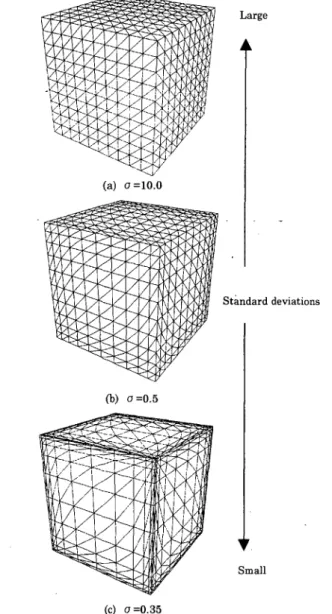
Fig. 4 FFDs of a cube with different standard deviations 次 に,式(9)に よ って 制 御 点 を 算 出 し,式(6)に よ っ てFFDを 実 行 す る.一 度FFDを 実 行 した 後 に,さ らに 操 作 点 の 移 動 や
吉 田 ・加 納 ・北 鳴:が ウ ス 関 数 に 基 づ くFree-FOrmDeformation
(a)σs=σt=σu=10.0
(b)
σs=10.0σt=0.05σn=0.01
(c)shade image of(a)(d)shadedimageof(b) Fig.5FFDsofacowmodel(1) 標 準 偏 差 の 変 更 も 可 能 で あ り,図3に 破 線 で 示 す よ う に 全 く 異 な る 操 作 点 を 配 置 し な お し て 変 形 す る こ と も 可 能 で あ る. 5.ガ ウ ス 関 数 に 基 づ くFFDを 用 い た 変 形 図4は,立 方 体 の コ ー ナ の8か 所 に 操 作 点 を 置 き,す べ て の 操 作 点 の 標 準 偏 差 を 変 え てFFDを 行 っ た と き の 立 方 体 の 変 形 す る 様 子 を 示 し て い る.立 方 体 は,各 軸 方 向 に 関 し て 等 間 隔 に パ ラ メ ー タ 化 さ れ て い る.図4(a)に 示 さ れ る よ う に, 標 準 偏 差 が 大 き い 場 合 に は パ ラ メー タ の 等 間 隔 性 が 保 た れ, 標 準 偏 差 が 小 さ く な る と,各 パ ラ メー タ 点 は 操 作 点 に 近 づ い て い く(図4(b),(c)).図4(a),(b),(c)に お け る す べ て の 操 作 点 の 標 準 偏 差 は,そ れ ぞ れ,10.0,0.5,035で あ る(標 準 偏 差 は モ デ ル の 大 き さ に 依 存 す る の で,各 モ デ ル の 座 標 は 0≦x,y,Z≦1と な る よ う に ス ケ ー リ ン グ さ れ て い る). 図5(a)は,cowモ デ ル を 囲 む 立 方 体 の 頂 点 上 に8個 の 操 作 点 を 配 置 した 図 で あ る.図5(b)は,こ の 状 態 か ら操 作 点 の 位 置 を変 え ず に,す べ て の 操 作 点 のtお よ びu方 向 の 標 準 偏 差 だ け を 小 さ く してFFDを 行 っ た も の で あ る.図5(c),(d)は,
(a)original cow model
(b)ƒÐ9 = 0.03
(c)ƒÐ9 = 0.1
(d)ƒÐ9 = 0.2
(e)shaded image of (d) Fig. 6 FFDs of a cow model (2)
吉 田 ・加 納 ・北嗚:が ウ ス 関 数 に 基 づ くFree-FormDeformation (a),(b)のモ デ ル に シ ェ ー デ ィ ン グ を施 した もの で あ る.こ の よ う に,ガ ウ ス 関 数 に 基 づ くFFDで は,操 作 点 を ま っ た く移 動 さ せ ず に 標 準 偏 差 を 変 え る こ と に よ る 変 形(こ の 場 合 は 太 ら せ る 変 形)が 可 能 で あ る.各 点 の 各 軸 方 向 の 標 準 偏 差 は 独 立 に 変 更 す る こ と が で き る の で,さ ら に 細 か な 調 整 も可 能 で あ る. 図6は,図5と 同 様 に8個 の 操 作 点,及 び 図6(a)に 矢 印 で 示 す 位 置 に 第9の 操 作 点 を 加 え た 図 で あ る.図6(b)は,第9 の 操 作 点 を 矢 印 に示 す 位 置 ま で 移 動 さ せ た 図 で あ る.図6(b) にお いて,第9の 操 作 点 の 標 準 偏 差(σ9)は 小 さ い の で,変 形 は局 所 的 で あ る.図6(c)は,第9の 操 作 点 の 標 準 偏 差 を 大 き く した も の で,操 作 点 の 移 動 の 影 響 範 囲 が 大 き く な っ て い る. 図6(d)は,標 準 偏 差 を さ ら に 大 き く し てFFDを 行 っ た も の で,変 形 が モ デ ル 全 体 に 影 響 し て い る こ と が 分 か る.図6 (b),(c),(d)にお け る 第9の 操 作 点 の 標 準 偏 差 は,そ れ ぞ れ,0.03, 0.1,0.2で あ り,そ の 他 の 操 作 点 の 標 準 偏 差 は す べ て10.0で あ る,図6(d)の モ デ ル に シ ェ ー デ ィ ン グ を施 し た も の を 図6 (e)に示 す. 6.他 のFFDと の 比 較 本 手 法 で 提 案 した ガ ウ ス 関 数 に 基 づ くFFD(以 下,本 手 法) は,Bernstein関 数 ま た はB-spline関 数 に 基 づ く 他 のFFDと 同様 に,変 形 さ れ る 形 状 モ デ ル に 独 立 で あ り,任 意 の ス プ ラ イ ン 曲 面.,ポ リ ゴ ン 曲 面,陰 関 数 曲 面 に応 用 す る こ と が で き る. 他 のFFDと は 異 な り,本 手 法 は,格 子 が 平 行 六 面 体 形 状 で あ る 必 要 が な く,任 意 に 制 御 点 を 配 置 す る こ と が で き る. Coquillartら は,任 意 の 格 子 でFFDを 行 う手 法 を 提 案 し て い るが,パ ラ メ ー タ 座 標(s,t,u)を 計 算 す る こ と が 容 易 で は な く, Newton法 を 用 い な け れ ば な ら な い.本 手 法 は,任 意 の 格 子 を 扱 う こ と が で き,か つ パ ラ メ ー タ 座 標 を 数 値 計 算 に よ っ て 算 出 す る こ と は 不 要 で あ る1本 手 法 で は,操 作 点 間 の 位 相 を ま った く必 要 と しな い 点 も特 徴 の 一 つ で あ る. 本 手 法 で は,操 作 点 を 任 意 に 配 置 す る こ と が で き る の で, 形 状 モ デ ル 上 の 点 を 直 接 操 作 す る こ と が で き る.Hsuら は, 直 接 変 形 が 可 能 なFFDの 手 法 を 提 案 して い る が,逆 行 列 が 一 意 に定 ま ら な い 場 合 が あ り,擬 似 逆 行 列 と い う概 念 を 利 用 し て い る.従 っ て,Hsuら の 手 法 で は,ユ ー ザ が 意 図 し な い形 状 に 変 形 す る 場 合 が あ る6).本 手 法 で は,直 接 操 作 が 可 能 で あ る が,逆 変 換 に よ っ て 逆 行 列 が 一 意 に 定 ま ら な い と い う こ と は 生 じな い. 対 話 的 な 操 作 を 実 現 す る た め に,ガ ウ ス 関 数 に 基 づ くFFD で は,任 意 の 場 所 に 操 作 点 を 追 加 し,影 響 範 囲 を 定 め る た め に 各 軸 方 向 の 標 準 偏 差 を 決 定 し,変 形 さ せ る こ と が 可 能 で あ る.さ ら に,変 形 後 に そ の 操 作 点 を 除 去 し,別 の 操 作 点 を追 加 す る こ と も可 能 で あ る.こ の よ う な 変 形 は,本 研 究 で 提 案 した ガ ウ ス 関 数 に 基 づ くFFDを 用 いて 可 能 と な る. 以 上 に 述 べ た よ う に,本 手 法 は,従 来 のFFDに は な い 特 徴 を 持 つ 新 し いFFDで あ る.本 手 法 のFFDは,特 別 な 拡 張 を 行 う こ と な く任 意 の 格 子 を 対 象 と す る こ と が で き る.従 っ て, モ デ ル の 直 接 操 作 が 可 能 で あ る.ま た,標 準 偏 差 を 変 更 す る こ と に よ っ て 操 作 点 の 移 動 の 影 響 範 囲 を 調 節 す る と い う 他 の FFDに は な い 特 徴 も も つ.本 手 法 を 応 用 す る こ と に よ っ て, 真 に 対 話 的 か つ 直 感 的 な モ デ リ ン グ が 可 能 とな る. 7.結 言 本 論 文 で は,ガ ウ ス 関 数 に基 づ くFree-FormDeformation を提 案 した.Bernstein関 数 やB-spline関 数 に 基 づ く 他 の FFDと 比 較 し て,本 手 法 は,以 下 の よ う な 特 長 を もつ. (1)任 意 個 の 制 御 点 を 任 意 の 位 置 に 設 定 す る こ と が で き る. 従 っ て,モ デ ル を 直 接 操 作 す る 変 形 が 可 能 とな る. (2)標 準 偏 差 を 変 え る こ と に よ っ て 操 作 点 の モ デ ル へ の 影 響 範 囲 を 変 え る こ と が で き る. こ れ に よ り,設 計 者 は 形 状 モ デ ル の 変 形 を 対 話 的 か つ 直 感 的 に行 う こ と が 可 能 と な る. 今 後 の 研 究 と して は,ガ ウ ス 関 数 に 基 づ くFFDの 特 長 を 生 か した 上 位 イ ン タ フ ェ ー ス の 作 成,及 び 多 重 解 像 表 現 尼)を利 用 す る こ と に よ る 複 雑 な モ デ ル へ の 対 応 な ど が あ げ ら れ る.現 在,本 手 法 を応 用 し た ア プ リケ ー シ ョ ン と し て,人 体 モ デ ル の 体 型 変 形 の 研 究 を行 っ て い る脚}.