有効ハミルトニアン法と密度汎関数法による原子の多重項状態エネルギー計算

─ ─285 （ ） は，明らかではない。特に，一つのスレータ行列では書 くことができない励起状態ネルギーが密度汎関数法によ り計算可能なのか，幾つかの試みはあるが，必ずしも明 らかではない。 従来の電子状態計算において，原子の各多重項エネル ギー計算にハートリー・フォック近似を行うと，nl軌道 電子間のクーロン相互作用エネルギーは動径方向波動関 数R（nl）の行列要素であるスレーター・コンドンパラ メータ： ・・・・・・・・・・・・・・・・（1） の線形結合により与えられ，実験スペクトルの多重項エ ネルギー値と比較検討された7 - 10）_{。しかし，定量的な一} 致は十分ではなかった。実験値と定量的な一致を得るた 1．序 非常に広い分野で密度汎関数法（DFT）による第一原 理計算が行われている。密度汎関数法における「物質の 基底状態の全エネルギーが電子密度の汎関数で記述でき る」という基本原理に基づき，多くの物質の基底状態， 安定構造，反応の遷移エネルギーなどに非常に多くの成 果が得られてきた1，2）_{。しかし，一方において，多くの} 問題のあることも知られている。特に，磁性・光物性な ど興味ある性質をもつ遷移金属・希土類金属化合物のよ うな電子相関の強い物質では局所密度近似（LSDA）だ けでは十分でなく，電子間相互作用を取り入れた，LDA ＋U，LDA-SIC，LDA＋GW などが行われている3 - 6）_。電 子相関効果は，特に原子内領域で大きいため，原子につ いての電子相関について明らかにすることが重要であ る。 密度汎関数法は基底状態エネルギーの値について信頼 性が保証されているが，励起状態エネルギーについて

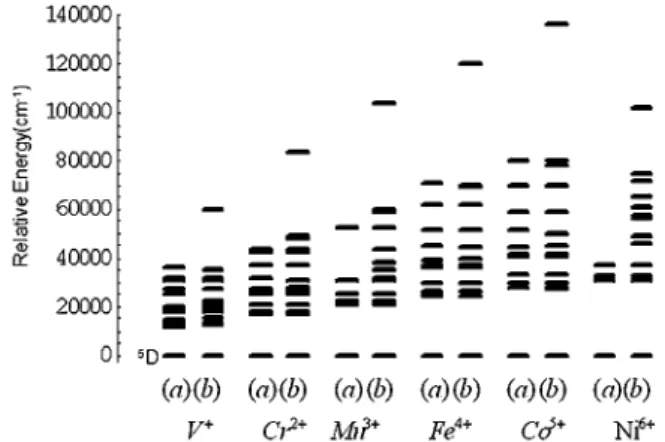
Multiplet terms for p3_{, d}4 _{and d}5 _{configurations are analyzed by the Effective Hamitonian in which the interaction}

between the electrons is composed of the sum of the screened Coulomb and the spin-denpendent screened Coulomb potential. All of the observed multiplet term energies of transition metal atoms can be fitted to ones calculated in the four modified Slater-Condon parameters within the limit of accuracy of few hundred cm-1_{. This means our proposed effective}

Hamitonian is meaningful to the calculation of the multiplet term energies in the strong correlated system . Then, we discuss whether these parameters can be produced by the calculation in the density functional method such as VWN potential and GGA potential. The result in the VWN potential is better than that in the GGA potential. It is pointed out that the spin-dependent screened Coulomb potential is important in the GGA potential.

Keywords: effective Hamiltonian, modified Slater-Condon parameter, multiplet terms energies, density functional method, VWN potential, GGA potential

有効ハミルトニアン法と密度汎関数法による

原子の多重項状態エネルギー計算

Chikatoshi SATOKO＊ （Accepted November 17, 2014） ＊ _{日本大学文理学部物理生命システム科学科：} 〒156-8550 東京都世田谷区桜上水3-25-40

＊ _{Department of Integrated Sciences in Physics and Biology, College of}

Humanities & Sciences, Nihon University 3-25-40 Sakurajousui, Setagaya-ku, Tokyo 156-8550, Japan

日本大学文理学部自然科学研究所研究紀要 No.50 （2015） pp.285−294

11

里 子 允 敏＊

Multiplet Term Energy Calculation of Transition Metal Atoms in the Effective Hamiltonian and Local Density Functional Methods

2 1 2 2 2 1 0 0 1 ( ) ( ) ) , ( R n l R nl drdr r r l n l n F k a a bb k b b a a k

∫∫

∞ ∞ + > < =

(

)

∑

− − − = i config i config i DF H H 2 δ

∑

= • = 4 0 2 ) ( 2 ) ( ) ( ) ( ) ( n n n eff a n U d U d H Ψ = Ψ E H n m n n P

∑

ψ ψ ≤ = ˆ 　 n m n n Q

∑

ψ ψ ≤ − = 1 ˆ Ψ + Ψ = Ψ Pˆ Qˆ Ψ Pˆ ) ( 2 ) ( d U n ) ˆ ( ) ˆ )( ˆ ˆ ˆ ˆ 1 ˆ ˆ ˆ ˆ ( Ψ = Ψ − + QHP P E P Q H Q E Q H P P H P n AV E E E⇒ ≈ P H Q Q H Q E Q H P P H P H av eff _{ˆ ˆ} ˆ ˆ 1 ˆ ˆ ˆ ˆ − + = 　 ) 2 ( ) 1 ( j i χ　 χ ) 2 ( ) 1 ( ), 2 ( ) 1 ( j i j i χ χ χ χ 　 　　　　　 )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 j i m m av m j i j i eff j i r E E r ij ij v χ χ ψ ψ χ χ χ χ χ χ − + > =< 　　　 m i m m E χ χ ψ ⇒ 3 : 　　　　　 　　　　　　 3 2 | 2 1 | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av j i eff j i E E im ij ij ij v − > < + > =< χ χ χ χ 　　　　　 　

∑

− + > =< m j i m m av m j i j i eff j i r E E r ij ij v )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 χ χ ψ ψ χ χ χ χ χ χ 　 　 ) ( 2 1 m i m i m χ χ χ χ ψ ⇒ + 　　　 ) ( 2 1 m i m i m χ χ χ χ ψ ⇒ − 1 2 3 2 | 4 1 | 4 1 | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av m av j i eff j i E E im ij E E im ij ij ij v − > < + − > < + > =< 　　　 χ χ χ χ 　　　　　 　　

∑

− + = m j i m m av m j i j i eff j i r E E r v )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( 0 )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 χ χ ψ ψ χ χ χ χ χ χ 1 2 3 2 | 4 1 | 4 1 )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av m av j i eff j i E E im ij E E im ij v − > < − − > < + = 　　　　 χ χ χ χ ) ( ) ( ) (12 12 1 2 ) 2 ( s s r w r v v ij ij ij eff = + ・ 　　　　　　 　　　

∑

− > < + − > < + > =< m av m av m ij E E im ij E E im ij ij ij r v ) | 8 1 | 8 3 ( | ) ( 1 2 3 2 12

∑

− < ₋ > − > < = m av m av m ij E E im ij E E im ij r w | ) 2 1 | 2 1 ( ) ( 1 2 3 2 12 　 　

∑

∑

∑

< < • + + = j i j i ij j i ij i i eff h v r w r s s H ( ) ( )

里　子　允　敏 ─ ─286 （ ）12 系で4 つのパラメータ係数a（1），a（2），a（3）， a（4）を 適当にとることにより，全ての多重項エネルギー観測値 が非常に近似よく再現できることが分かった。しかし， （3）式が対称性を基本にした理論から作られており，電 子間相互作用の物理的な描像を描きにくい面があった。 そこで，この論文では，電子相関を陽に取り入れた具 体的な有効2 体相互作用を導入し，原子スペクトルの観 測値並びに密度汎関数法による計算を組み合わせ，電子 間相関効果を明らかにすることを提案する。 2．有効ハミルトニアン法 多体シレディンガー方程式 ・・・・・・・・・・・・・・・・（4） は複雑すぎて厳密に解くことは困難である。 そこで， 簡単で解くべき固有エネルギーE と同じあるいは近い固 有エネルギーを与える有効ハミルトニアンをつくり，そ れを解くことが多い。ある波動関数｛ψn，n＝1，2,,,m｝ の内部状態空間に制限する射影演算子 ・・・・・・・・・・・・・・・・（5） と，それ以外の波動関数に制限する射影演算子 ・・・・・・・・・・・・・・・・（6） を定義すると波動関数Ψは ・・・・・・・・・・・・・・・・（7） と書くことができる。簡単な計算により，内部状態空間 に射影した波動関数　　に関する方程式（フェッシュ バッハ方程式） ・・・・・・・・・・・・・・・・（8） めにはハートリー・フォック近似計算より得られたス レーター・コンドンパラメータの値より，小さい値にす る必要があった11）_{。この不一致の原因はハートリフォッ} ク近似のためで，その近似を超えるためには多くの電子 配置間相互作用計算を行う必要があった。しかし，数 百万程度以上の電子配置間相互作用計算を行っても，必 ずしも定量的な遷移金属原子の多重項エネルギーを得る ことは困難であった12，13）_。 近年，電子相関効果を取り入れた密度汎関数法により， スレーター・コンドンパラメータ値を求める計算が行わ れた。密度汎関数法において，一つのスレーター行列 （i-config）で表される状態の全エネルギー＜ HDF＞が計 算できる。一方で，それらの状態の全エネルギー＜H ＞ はスレーター・コンドンパラメータの線形結合でも表さ れる。そこで，密度汎関数法で求めた種々の電子配置の エネルギー値を再現できるように，下記の式： ・・・・・・・・・・・・・・・・（2） を最小化して，最適一致するスレーター・コンドンパラ メータの値を得た（i-configはi = 1, 2, 3, 4, , , , , , ,と種々の 電子配置の状態）。その結果，ハートリー・フォック近 似の計算値より縮小したスレーター・コンドンパラメー タ値が得られたが，実験との一致は必ずしも改善されて いない14）_{。その原因はスレーター・コンドンパラメータ} の線形結合で書かれた全エネルギー＜H ＞が，ハート リ・フォック近似から出発した相関効果の入っていない 理論計算から得られた全エネルギーであり，一方，密度 汎関数法による＜HDF＞は電子相関を取り入れた全エネ ルギーで，その両者において電子相関効果の理論的バラ ンスがとれていないためである。 強い電子相関効果を考えるために，電子相関効果を明 確に取り入れた理論が必要となる。そこで，遷移金属原 子の多重項エネルギーを単位テンソル演算子U （n）_（d 2 _） のスカラー積和の有効ハミルトニアン ・・・・・・・・・・・・・・・・（3） が提案され，電子相関効果が調べられた（この有効ハミ ルトニアンは，ハートリ・フォック近似のとき，a（1） = 0，a（3） = 0となることが示される）15，16）_{。そして，d電子} 2 1 2 2 2 1 0 0 1 ( ) ( ) ) , ( R n l R nl drdr r r l n l n F _{k a a bb} k b b a a k

∫∫

∞ ∞ + > < =

(

)

∑

− − − = i config i config i DF H H 2 δ

∑

= • = 4 0 2 ) ( 2 ) ( ) ( ) ( ) ( n n n eff a nU d U d H Ψ = Ψ E H n m n n P

∑

ψ ψ ≤ = ˆ 　 n m n n Q

∑

ψ ψ ≤ − = 1 ˆ Ψ + Ψ = Ψ Pˆ Qˆ Ψ Pˆ ) ( 2 ) ( d U n ) ˆ ( ) ˆ )( ˆ ˆ ˆ ˆ 1 ˆ ˆ ˆ ˆ ( Ψ = Ψ − + QHP P E P Q H Q E Q H P P H P n AV E E E⇒ ≈ P H Q Q H Q E Q H P P H P H av eff ˆ ˆ ˆ ˆ 1 ˆ ˆ ˆ ˆ − + = 　 ) 2 ( ) 1 ( _j i χ　 χ ) 2 ( ) 1 ( ), 2 ( ) 1 ( _{j i j} i χ χ χ χ 　 　　　　　 )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 j i m m av m j i j i eff j i r E E r ij ij v χ χ ψ ψ χ χ χ χ χ χ − + > =< 　　　 m i m m E χ χ ψ ⇒ ₃ : 　　　　　 　　　　　　 3 2 | 2 1 | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av j i eff j i E E im ij ij ij v − > < + > =< χ χ χ χ 　　　　　 　

∑

− + > =< m j i m m av m j i j i eff j i r E E r ij ij v )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 χ χ ψ ψ χ χ χ χ χ χ 　 　 ) ( 2 1 m i m i m χ χ χ χ ψ ⇒ + 　　　 ) ( 2 1 m i m i m χ χ χ χ ψ ⇒ − 1 2 3 2 | 4 1 | 4 1 | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av m av j i eff j i E E im ij E E im ij ij ij v − > < + − > < + > =< 　　　 χ χ χ χ 　　　　　 　　

∑

− + = m j i m m av m j i j i eff j i r E E r v )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( 0 )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 χ χ ψ ψ χ χ χ χ χ χ 1 2 3 2 | 4 1 | 4 1 )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av m av j i eff j i E E im ij E E im ij v − > < − − > < + = 　　　　 χ χ χ χ ) ( ) ( ) (_{12 12 1 2} ) 2 ( s s r w r v v _{ij ij} ij eff = + ・ 　　　　　　 　　　

∑

− > < + − > < + > =< m av m av m ij E E im ij E E im ij ij ij r v ) | 8 1 | 8 3 ( | ) ( 1 2 3 2 12

∑

− < ₋ > − > < = m av m av m ij E E im ij E E im ij r w | ) 2 1 | 2 1 ( ) ( 1 2 3 2 12 　 　

∑

∑

∑

< < • + + = j i j i ij j i ij i i eff h v r w r s s H ( ) ( ) 2 1 2 2 2 1 0 0 1 ( ) ( ) ) , ( R n l R nl drdr r r l n l n F _{k a a b b} k b b a a k

∫∫

∞ ∞ + > < =

(

)

∑

− − − = i config i config i DF H H 2 δ

∑

= • = 4 0 2 ) ( 2 ) ( ) ( ) ( ) ( n n n eff a nU d U d H Ψ = Ψ E H n m n n P

∑

ψ ψ ≤ = ˆ 　 n m n n Q

∑

ψ ψ ≤ − = 1 ˆ Ψ + Ψ = Ψ Pˆ Qˆ Ψ Pˆ ) ( 2 ) ( d U n ) ˆ ( ) ˆ )( ˆ ˆ ˆ ˆ 1 ˆ ˆ ˆ ˆ ( Ψ = Ψ − + QHP P E P Q H Q E Q H P P H P n AV E E E⇒ ≈ P H Q Q H Q E Q H P P H P H av eff _{ˆ ˆ} ˆ ˆ 1 ˆ ˆ ˆ ˆ − + = 　 ) 2 ( ) 1 ( _j i χ　 χ ) 2 ( ) 1 ( ), 2 ( ) 1 ( _{j i j} i χ χ χ χ 　 　　　　　 )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 j i m m av m j i j i eff j i r E E r ij ij v χ χ ψ ψ χ χ χ χ χ χ − + > =< 　　　 m i m m E χ χ ψ ⇒ ₃ : 　　　　　 　　　　　　 3 2 | 2 1 | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av j i eff j i E E im ij ij ij v − > < + > =< χ χ χ χ 　　　　　 　

∑

− + > =< m j i m m av m j i j i eff j i r E E r ij ij v )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 χ χ ψ ψ χ χ χ χ χ χ 　 　 ) ( 2 1 m i m i m χ χ χ χ ψ ⇒ + 　　　 ) ( 2 1 m i m i m χ χ χ χ ψ ⇒ − 1 2 3 2 | 4 1 | 4 1 | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av m av j i eff j i E E im ij E E im ij ij ij v − > < + − > < + > =< 　　　 χ χ χ χ 　　　　　 　　

∑

− + = m j i m m av m j i j i eff j i r E E r v )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( 0 )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 χ χ ψ ψ χ χ χ χ χ χ 1 2 3 2 | 4 1 | 4 1 )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av m av j i eff j i E E im ij E E im ij v − > < − − > < + = 　　　　 χ χ χ χ ) ( ) ( ) (12 12 1 2 ) 2 ( s s r w r v v_{eff ij} = ij + ij ・ 　　　　　　 　　　

∑

− > < + − > < + > =< m av m av m ij E E im ij E E im ij ij ij r v ) | 8 1 | 8 3 ( | ) ( 1 2 3 2 12

∑

− < ₋ > − > < = m av m av m ij E E im ij E E im ij r w | ) 2 1 | 2 1 ( ) ( 1 2 3 2 12 　 　

∑

∑

∑

< < • + + = j i j i ij j i ij i i eff h v r w r s s H ( ) ( ) 2 1 2 2 2 1 0 0 1 ( ) ( ) ) , ( R n l R nl drdr r r l n l n F _{k a a bb} k b b a a k

∫∫

∞ ∞ + > < =

(

)

∑

− − − = i config i config i DF H H 2 δ

∑

= • = 4 0 2 ) ( 2 ) ( ) ( ) ( ) ( n n n eff a nU d U d H Ψ = Ψ E H n m n n P

∑

ψ ψ ≤ = ˆ 　 n m n n Q

∑

ψ ψ ≤ − = 1 ˆ Ψ + Ψ = Ψ Pˆ Qˆ Ψ Pˆ ) ( 2 ) ( d U n ) ˆ ( ) ˆ )( ˆ ˆ ˆ ˆ 1 ˆ ˆ ˆ ˆ ( Ψ = Ψ − + QHP P E P Q H Q E Q H P P H P n AV E E E⇒ ≈ P H Q Q H Q E Q H P P H P H av eff _{ˆ ˆ} ˆ ˆ 1 ˆ ˆ ˆ ˆ − + = 　 ) 2 ( ) 1 ( _j i χ　 χ ) 2 ( ) 1 ( ), 2 ( ) 1 ( _{j i j} i χ χ χ χ 　 　　　　　 )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 j i m m av m j i j i eff j i r E E r ij ij v χ χ ψ ψ χ χ χ χ χ χ − + > =< 　　　 m i m m E χ χ ψ ⇒ ₃ : 　　　　　 　　　　　　 3 2 | 2 1 | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av j i eff j i E E im ij ij ij v − > < + > =< χ χ χ χ 　　　　　 　

∑

− + > =< m j i m m av m j i j i eff j i r E E r ij ij v )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 χ χ ψ ψ χ χ χ χ χ χ 　 　 ) ( 2 1 m i m i m χ χ χ χ ψ ⇒ + 　　　 ) ( 2 1 m i m i m χ χ χ χ ψ ⇒ − 1 2 3 2 | 4 1 | 4 1 | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av m av j i eff j i E E im ij E E im ij ij ij v − > < + − > < + > =< 　　　 χ χ χ χ 　　　　　 　　

∑

− + = m j i m m av m j i j i eff j i r E E r v )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( 0 )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 χ χ ψ ψ χ χ χ χ χ χ 1 2 3 2 | 4 1 | 4 1 )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av m av j i eff j i E E im ij E E im ij v − > < − − > < + = 　　　　 χ χ χ χ ) ( ) ( ) (_{12 12 1 2} ) 2 ( s s r w r v v _{ij ij} ij eff = + ・ 　　　　　　 　　　

∑

− > < + − > < + > =< m av m av m ij E E im ij E E im ij ij ij r v ) | 8 1 | 8 3 ( | ) ( 1 2 3 2 12

∑

− < ₋ > − > < = m av m av m ij E E im ij E E im ij r w | ) 2 1 | 2 1 ( ) ( 1 2 3 2 12 　 　

∑

∑

∑

< < • + + = j i j i ij j i ij i i eff h v r w r s s H ( ) ( ) 2 1 2 2 2 1 0 0 1 ( ) ( ) ) , ( R nl R n l drdr r r l n l n F k a a b b k b b a a k

∫∫

∞ ∞ + > < =

(

)

∑

− − − = i config i config i DF H H 2 δ

∑

= • = 4 0 2 ) ( 2 ) ( ) ( ) ( ) ( n n n eff a nU d U d H Ψ = Ψ E H n m n n P

∑

ψ ψ ≤ = ˆ 　 n m n n Q

∑

ψ ψ ≤ − = 1 ˆ Ψ + Ψ = Ψ Pˆ Qˆ Ψ Pˆ ) ( 2 ) ( d U n ) ˆ ( ) ˆ )( ˆ ˆ ˆ ˆ 1 ˆ ˆ ˆ ˆ ( Ψ = Ψ − + QHP P E P Q H Q E Q H P P H P n AV E E E⇒ ≈ P H Q Q H Q E Q H P P H P H av eff _{ˆ ˆ} ˆ ˆ 1 ˆ ˆ ˆ ˆ − + = 　 ) 2 ( ) 1 ( j i χ　 χ ) 2 ( ) 1 ( ), 2 ( ) 1 ( j i j i χ χ χ χ 　 　　　　　 )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 j i m m av m j i j i eff j i r E E r ij ij v χ χ ψ ψ χ χ χ χ χ χ − + > =< 　　　 m i m m E χ χ ψ ⇒ 3 : 　　　　　 　　　　　　 3 2 | 2 1 | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av j i eff j i E E im ij ij ij v − > < + > =< χ χ χ χ 　　　　　 　

∑

− + > =< m j i m m av m j i j i eff j i r E E r ij ij v )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 χ χ ψ ψ χ χ χ χ χ χ 　 　 ) ( 2 1 m i m i m χ χ χ χ ψ ⇒ + 　　　 ) ( 2 1 m i m i m χ χ χ χ ψ ⇒ − 1 2 3 2 | 4 1 | 4 1 | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av m av j i eff j i E E im ij E E im ij ij ij v − > < + − > < + > =< 　　　 χ χ χ χ 　　　　　 　　

∑

− + = m j i m m av m j i j i eff j i r E E r v )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( 0 )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 χ χ ψ ψ χ χ χ χ χ χ 1 2 3 2 | 4 1 | 4 1 )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av m av j i eff j i E E im ij E E im ij v − > < − − > < + = 　　　　 χ χ χ χ ) ( ) ( ) ( _{12 12 1 2} ) 2 ( s s r w r v v _{ij ij} ij eff = + ・ 　　　　　　 　　　

∑

− > < + − > < + > =< m av m av m ij E E im ij E E im ij ij ij r v ) | 8 1 | 8 3 ( | ) ( 1 2 3 2 12

∑

− < ₋ > − > < = m av m av m ij E E im ij E E im ij r w | ) 2 1 | 2 1 ( ) ( 1 2 3 2 12 　 　

∑

∑

∑

< < • + + = j i j i ij j i ij i i eff h v r w r s s H ( ) ( ) 2 1 2 2 2 1 0 0 1 ( ) ( ) ) , ( R n l R nl drdr r r l n l n F _{k a a b b} k b b a a k

∫∫

∞ ∞ + > < =

(

)

∑

− − − = i config i config i DF H H 2 δ

∑

= • = 4 0 2 ) ( 2 ) ( ) ( ) ( ) ( n n n eff a nU d U d H Ψ = Ψ E H n m n n P

∑

ψ ψ ≤ = ˆ 　 n m n n Q

∑

ψ ψ ≤ − = 1 ˆ Ψ + Ψ = Ψ Pˆ Qˆ Ψ Pˆ ) ( 2 ) ( d U n ) ˆ ( ) ˆ )( ˆ ˆ ˆ ˆ 1 ˆ ˆ ˆ ˆ ( Ψ = Ψ − + QHP P E P Q H Q E Q H P P H P n AV E E E⇒ ≈ P H Q Q H Q E Q H P P H P H av eff _{ˆ ˆ} ˆ ˆ 1 ˆ ˆ ˆ ˆ − + = 　 ) 2 ( ) 1 ( _j i χ　 χ ) 2 ( ) 1 ( ), 2 ( ) 1 ( _{j i j} i χ χ χ χ 　 　　　　　 )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 j i m m av m j i j i eff j i r E E r ij ij v χ χ ψ ψ χ χ χ χ χ χ − + > =< 　　　 m i m m E χ χ ψ ⇒ ₃: 　　　　　 　　　　　　 3 2 | 2 1 | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av j i eff j i E E im ij ij ij v − > < + > =< χ χ χ χ 　　　　　 　

∑

− + > =< m j i m m av m j i j i eff j i r E E r ij ij v )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 χ χ ψ ψ χ χ χ χ χ χ 　 　 ) ( 2 1 m i m i m χ χ χ χ ψ ⇒ + 　　　 ) ( 2 1 m i m i m χ χ χ χ ψ ⇒ − 1 2 3 2 | 4 1 | 4 1 | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av m av j i eff j i E E im ij E E im ij ij ij v − > < + − > < + > =< 　　　 χ χ χ χ 　　　　　 　　

∑

− + = m j i m m av m j i j i eff j i r E E r v )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( 0 )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 χ χ ψ ψ χ χ χ χ χ χ 1 2 3 2 | 4 1 | 4 1 )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av m av j i eff j i E E im ij E E im ij v − > < − − > < + = 　　　　 χ χ χ χ ) ( ) ( ) ( _{12 12 1 2} ) 2 ( s s r w r v v _{ij ij} ij eff = + ・ 　　　　　　 　　　

∑

− > < + − > < + > =< m av m av m ij E E im ij E E im ij ij ij r v ) | 8 1 | 8 3 ( | ) ( 1 2 3 2 12

∑

− < ₋ > − > < = m av m av m ij E E im ij E E im ij r w | ) 2 1 | 2 1 ( ) ( 1 2 3 2 12 　 　

∑

∑

∑

< < • + + = j i j i ij j i ij i i eff h v r w r s s H ( ) ( ) 2 1 2 2 2 1 0 0 1 ( ) ( ) ) , ( R n l R nl drdr r r l n l n F _{k a a b b} k b b a a k

∫∫

∞ ∞ + > < =

(

)

∑

− − − = i config i config i DF H H 2 δ

∑

= • = 4 0 2 ) ( 2 ) ( ) ( ) ( ) ( n n n eff a nU d U d H Ψ = Ψ E H n m n n P

∑

ψ ψ ≤ = ˆ 　 n m n n Q

∑

ψ ψ ≤ − = 1 ˆ Ψ + Ψ = Ψ Pˆ Qˆ Ψ Pˆ ) ( 2 ) ( d U n ) ˆ ( ) ˆ )( ˆ ˆ ˆ ˆ 1 ˆ ˆ ˆ ˆ ( Ψ = Ψ − + QHP P E P Q H Q E Q H P P H P n AV E E E⇒ ≈ P H Q Q H Q E Q H P P H P H av eff _{ˆ ˆ} ˆ ˆ 1 ˆ ˆ ˆ ˆ − + = 　 ) 2 ( ) 1 ( j i χ　 χ ) 2 ( ) 1 ( ), 2 ( ) 1 ( _{j i j} i χ χ χ χ 　 　　　　　 )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 j i m m av m j i j i eff j i r E E r ij ij v χ χ ψ ψ χ χ χ χ χ χ − + > =< 　　　 m i m m E χ χ ψ ⇒ ₃: 　　　　　 　　　　　　 3 2 | 2 1 | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av j i eff j i E E im ij ij ij v − > < + > =< χ χ χ χ 　　　　　 　

∑

− + > =< m j i m m av m j i j i eff j i r E E r ij ij v )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 χ χ ψ ψ χ χ χ χ χ χ 　 　 ) ( 2 1 m i m i m χ χ χ χ ψ ⇒ + 　　　 ) ( 2 1 m i m i m χ χ χ χ ψ ⇒ − 1 2 3 2 | 4 1 | 4 1 | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av m av j i eff j i E E im ij E E im ij ij ij v − > < + − > < + > =< 　　　 χ χ χ χ 　　　　　 　　

∑

− + = m j i m m av m j i j i eff j i r E E r v )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( 0 )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 χ χ ψ ψ χ χ χ χ χ χ 1 2 3 2 | 4 1 | 4 1 )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av m av j i eff j i E E im ij E E im ij v − > < − − > < + = 　　　　 χ χ χ χ ) ( ) ( ) ( 12 12 1 2 ) 2 ( s s r w r v v_{eff ij} = ij + ij ・ 　　　　　　 　　　

∑

− > < + − > < + > =< m av m av m ij E E im ij E E im ij ij ij r v ) | 8 1 | 8 3 ( | ) ( 1 2 3 2 12

∑

− < ₋ > − > < = m av m av m ij E E im ij E E im ij r w | ) 2 1 | 2 1 ( ) ( 1 2 3 2 12 　 　

∑

∑

∑

< < • + + = j i j i ij j i ij i i eff h v r w r s s H ( ) ( ) 2 1 2 2 2 1 0 0 1 ( ) ( ) ) , ( R n l R n l drdr r r l n l n F k a a b b k b b a a k

∫∫

∞ ∞ + > < =

(

)

∑

− − − = i config i config i DF H H 2 δ

∑

= • = 4 0 2 ) ( 2 ) ( ) ( ) ( ) ( n n n eff a nU d U d H Ψ = Ψ E H n m n n P

∑

ψ ψ ≤ = ˆ 　 n m n n Q

∑

ψ ψ ≤ − = 1 ˆ Ψ + Ψ = Ψ Pˆ Qˆ Ψ Pˆ ) ( 2 ) ( d U n ) ˆ ( ) ˆ )( ˆ ˆ ˆ ˆ 1 ˆ ˆ ˆ ˆ ( Ψ = Ψ − + QHP P E P Q H Q E Q H P P H P n AV E E E⇒ ≈ P H Q Q H Q E Q H P P H P H av eff _{ˆ ˆ} ˆ ˆ 1 ˆ ˆ ˆ ˆ − + = 　 ) 2 ( ) 1 ( j i χ　 χ ) 2 ( ) 1 ( ), 2 ( ) 1 ( j i j i χ χ χ χ 　 　　　　　 )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 j i m m av m j i j i eff j i r E E r ij ij v χ χ ψ ψ χ χ χ χ χ χ − + > =< 　　　 m i m m E χ χ ψ ⇒ 3 : 　　　　　 　　　　　　 3 2 | 2 1 | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av j i eff j i E E im ij ij ij v − > < + > =< χ χ χ χ 　　　　　 　

∑

− + > =< m j i m m av m j i j i eff j i r E E r ij ij v )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 χ χ ψ ψ χ χ χ χ χ χ 　 　 ) ( 2 1 m i m i m χ χ χ χ ψ ⇒ + 　　　 ) ( 2 1 m i m i m χ χ χ χ ψ ⇒ − 1 2 3 2 | 4 1 | 4 1 | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av m av j i eff j i E E im ij E E im ij ij ij v − > < + − > < + > =< 　　　 χ χ χ χ 　　　　　 　　

∑

− + = m j i m m av m j i j i eff j i r E E r v )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( 0 )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 χ χ ψ ψ χ χ χ χ χ χ 1 2 3 2 | 4 1 | 4 1 )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av m av j i eff j i E E im ij E E im ij v − > < − − > < + = 　　　　 χ χ χ χ ) ( ) ( ) ( _{12 12 1 2} ) 2 ( s s r w r v v _{ij ij} ij eff = + ・ 　　　　　　 　　　

∑

− > < + − > < + > =< m av m av m ij E E im ij E E im ij ij ij r v ) | 8 1 | 8 3 ( | ) ( 1 2 3 2 12

∑

− < ₋ > − > < = m av m av m ij E E im ij E E im ij r w | ) 2 1 | 2 1 ( ) ( 1 2 3 2 12 　 　

∑

∑

∑

< < • + + = j i j i ij j i ij i i eff h v r w r s s H ( ) ( ) 2 1 2 2 2 1 0 0 1 ( ) ( ) ) , ( R nl R nl drdr r r l n l n F _{k a a bb} k b b a a k

∫∫

∞ ∞ + > < =

(

)

∑

− − − = i i config i config DF H H 2 δ

∑

= • = 4 0 2 ) ( 2 ) ( ) ( ) ( ) ( n n n eff a nU d U d H Ψ = Ψ E H n m n n P

∑

ψ ψ ≤ = ˆ 　 n m n n Q

∑

ψ ψ ≤ − = 1 ˆ Ψ + Ψ = Ψ Pˆ Qˆ Ψ Pˆ ) ( 2 ) ( _d U n ) ˆ ( ) ˆ )( ˆ ˆ ˆ ˆ 1 ˆ ˆ ˆ ˆ ( Ψ = Ψ − + QHP P E P Q H Q E Q H P P H P n AV E E E⇒ ≈ P H Q Q H Q E Q H P P H P H av eff _{ˆ ˆ} ˆ ˆ 1 ˆ ˆ ˆ ˆ − + = 　 ) 2 ( ) 1 ( _j i χ　 χ ) 2 ( ) 1 ( ), 2 ( ) 1 ( _{j i j} i χ χ χ χ 　 　　　　　 )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 j i m m av m j i j i eff j i r E E r ij ij v χ χ ψ ψ χ χ χ χ χ χ − + > =< 　　　 m i m m E χ χ ψ ⇒ ₃: 　　　　　 　　　　　　 3 2 | 2 1 | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av j i eff j i E E im ij ij ij v − > < + > =< χ χ χ χ 　　　　　 　∑ − + > =< m j i m m av m j i j i eff j i r E E r ij ij v )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 χ χ ψ ψ χ χ χ χ χ χ 　 　 ) ( 2 1 m i m i m χχ χ χ ψ ⇒ + 　　　 ) ( 2 1 m i m i m χ χ χχ ψ ⇒ − 1 2 3 2 _| 4 1 | 4 1 | )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av m av j i eff j i E E im ij E E im ij ij ij v − > < + − > < + > =< 　　　 χ χ χ χ 　　　　　 　　∑ − + = m j i m m av m j i j i eff j i r E E r v )) 2 ( ) 1 ( 1 , ( 1 ) 1 ), 2 ( ) 1 ( ( 0 )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( 12 12 χ χ ψ ψ χ χ χ χ χ χ 1 2 3 2 | 4 1 | 4 1 )) 2 ( ) 1 ( ), 2 ( ) 1 ( ( m av m av j i eff j i E E im ij E E im ij v − > < − − > < + = 　　　　 χ χ χ χ ) ( ) ( ) (_{12 12 1 2} ) 2 ( _{v r wr s s} v _{ij ij} ij eff = + ・ 　　　　　　 　　　

∑

− > < + − > < + > =< m av m av m ij E E im ij E E im ij ij ij r v ) | 8 1 | 8 3 ( | ) ( 1 2 3 2 12

∑

− < ₋ > − > < = m av m av m ij E E im ij E E im ij r w | ) 2 1 | 2 1 ( ) ( 1 2 3 2 12 　 　

∑

∑

∑

< < • + + = j i j i ij j i ij i i eff h v r wr s s H ( ) ( )