第3章コヒーレント状態
(3.5
∼
3.8)
0303121s西村睦実2006.7.101
コヒーレント状態の性質
数状態|ni(n = 0, 1, ...)は正規直交hn|n0i = δnn0 で完全性 ∞ X n=0 |nihn| = Iを満たす。電磁場の単一モード の任意の状態ベクトルは数状態で展開できる。 |ψi =X n Cn|ni (1) ここで、Cn= hn|ψi。 コヒーレント状態は数状態を用いて |αi = e−12|α|2 ∞ X n=0 αn √ n!|ni (2) と表される。α, βに対応するコヒーレント状態の内積をとると、 hβ|αi = e−1 2|α|2−12|β|2 ∞ X n=0 ∞ X m=0 β∗nαm √ n!m!hn|mi = e−1 2|α|2−12|β|2 ∞ X n=0 β∗nαm n! = e−1 2|α|2−12|β|2+β∗α = e12(β∗α−βα∗)e−12|β−α|2 6= 0 (3) よって、コヒーレント状態は直交していない。ただし|β − α|2À 1のときはほぼ直交していると見なせる。 コヒーレント状態は完全性*1、 Z |αihα|d 2α π = 1 (4) を満たす。従って単一モード場に量子化されたヒルベルト空間における状態|ψiはすべて、コヒーレント状態 によって次のように表される。 |ψi = Z d2α π |αihα|ψi (5) 特に、|ψi = |βi ととると、 |βi = Z d2α π |αihα|βi = Z d2α π |αie −1 2|α|2−12|β|2+α∗β (6) よって、コヒーレント状態は一次独立でないことがわかる。 *1付録参照ˆ
Fをˆa、ˆa†の関数、F = ˆˆ F (ˆa, ˆa†)とする。Fˆは数状態で、 ˆ F =X n X m |mihm| ˆF |nihn| =X n X m |miFmnhn| (7) と展開できる。ここで、Fmn= hm| ˆF |niは Fˆのmn成分 。 次に、コヒーレント状態で展開をすると、 ˆ F = 1 π2 Z d2β Z d2α|βihβ| ˆF |αihα| (8) ここで、 hβ| ˆF |αi =X n X m Fmnhβ|mihn|αi = e−1 2(|β|2+|α|2)F (β∗, α) (9) ただし、 F (β∗, α) =X n X m Fmn(β ∗)m(α)n √ m!n! (10) と定義した。よって ˆ F = 1 π2 Z d2β Z d2α e−1 2(|β|2+|α|2)F (β∗, α)|βihα| (11) と表すことができる。 今、Fˆがエルミート演算子で固有状態|λiによって、 ˆ F =X λ λ|λihλ| (12) と表せるとすると、 Fmn=X λ λhm|λihλ|ni (13) |Fmn| ≤X λ λ|hm|λihλ|ni| ≤X λ λ = T r ˆF (14) このことは、|Fmn|に上限があることを意味する。これは、F (β∗, α)が、β∗、αの両方について 整関数である ことを示す。 コヒーレント状態についてのFˆ の対角成分がこの演算子Fˆを決定する。式(9),(10)より、 hα| ˆF |αieα∗α =X n X m α∗mαn √ m!n!hm| ˆF |ni (15) αとα∗は独立変数とあつかえるので、 1 √ m!n! " ∂n+m(hα| ˆF |αieα∗α ∂α∗m∂αn # ¯ ¯ ¯ ¯ ¯ α∗=0,α=0 = hm| ˆF |ni (16) よって、コヒーレント状態のFˆの対角成分だけから、数基底の演算子の行列要素の全てを得ることができる。
2
コヒーレント状態の位相空間
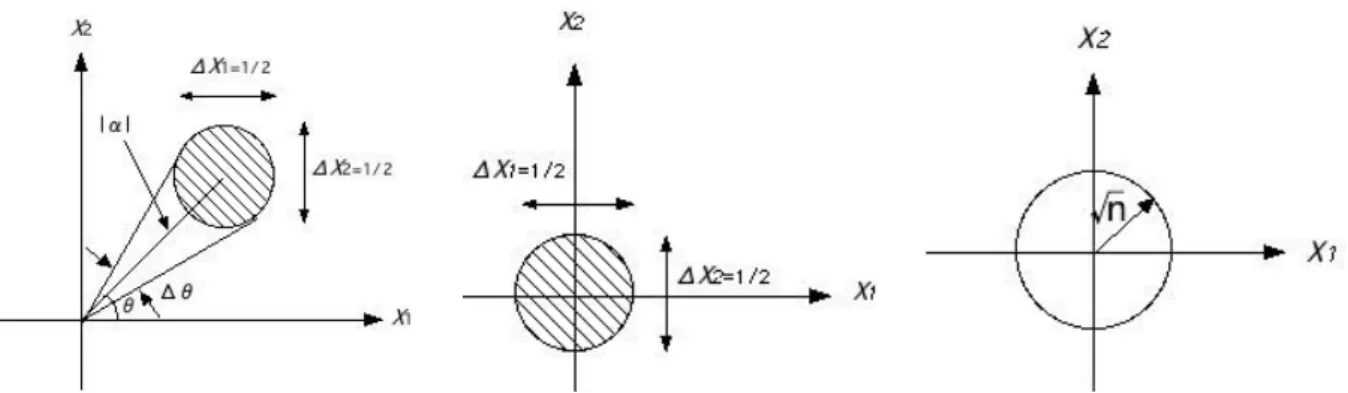
コヒーレント状態が位相空間でどう描かれるかを考えていく。 量子力学では変数xˆとpˆが交換しないため、物理的状態を位相空間上の点で表すことができない。しかし、 コヒーレント状態においては、xˆとpˆの不確定性関係は最小になり、それぞれのゆらぎが等しくなる。 ここで、第2章で定義した、Quadratureオペレータ*2を用導入する。 ˆ X1= ˆa + ˆa † 2 Xˆ2= ˆa − ˆa† 2i (17) ˆ X1、Xˆ2のコヒーレン状態での期待値は、 h ˆX1i = hα|1 2(ˆa + ˆa †)|αi =1 2(α + α ∗) = Re(α) (18) h ˆX2i = hα|1 2(ˆa − ˆa †)|αi = 1 2(α − α ∗) = Im(α) (19) つまり、複素数α平面の実数部がXˆ1に、虚数部がXˆ2にそれぞれ対応している。また、真空におけるゆらぎの 二乗平均は、 h(∆ ˆX1)2i = 1 4 = h(∆ ˆX2) 2i (20) である。複素数|αi = |α|eiθに対応するコビーレンと状態|αiは(X
1, X2)平面上で、図1(左)のように描かれる。 ここで、斜線部はコヒーレント状態における不確定性の範囲を表す。このゆらぎは位相空間上どこでも等し く*3正確、円の中心は原点から距離|α|、Xˆ1軸から角度θの位置である。また、|α|を大きくすると位相 θの ゆらぎ∆θが小さくなる。|α| = 0のとき、図1(中)のようになり、このとき位相のゆらぎは最大で、∆θ = 2π となる。 一方、数状態|niは位相空間において、半径√nの円で描かれる。nのゆらぎは0で、位相のゆらぎは2π (図1右)。 次に、相互作用のない場での量子状態の時間発展を描いてみよう。相互作用のないとき、コヒーレント状態
|αiは、時間発展すると、|αe−iωtiとなる。 hαe−iωt| ˆX
1|αe−iωti = α cos ωt
hαe−iωt| ˆX2|αe−iωti = −α sin ωt
(21) よって、コヒーレント状態は位相空間においてゆらぎの円(error circle)の時計回りとして描かれる(図2)。
電場は、
ˆ
Ex(z, t) = εo(ˆa + ˆa†) sin(kz) = 2εosin(kz) ˆX1
(22)
*2 それぞれ、位置ˆxと運動量ˆp に対応している。Introductry Quantum Optics §2-3 を参照
図1 位相空間におけるコヒーレント状態(左、中)と数状態(右)
図2 位相空間におけるコヒーレント状態の時間発展
として与えられるので、コヒーレント状態における期待値は、
hαe−iωt| ˆEx|αe−iωti = 2εoα sin(kz) cos(ωt) (23)
となる。よって、電場はゆらぎの時間発展のXˆ1軸への投影によって時間の関数として与えられる(図2)。こ こで、error circle内の点の時間発展は電場の不確定性を示している。
3
密度演算子と位相空間の確率分布
量子状態、|ψ1i|ψ2i...の重ね合わせにおける密度演算子は、 ˆ ρ =X i pi|ψiihψi| (24) と与えられる。ここで、piは、i番目の状態にある系が観測される確率を表す。また、全確率は1である。 T r(ˆρ) =X i pi= 1 (25) 任意の演算子、oˆの期待値は、 hˆoi = T r(ˆoˆρ) =X i pihψo|ˆo|ψii (26)と与えられる。方程式、(7)より、密度演算子は数状態によって、 ˆ ρ =X n X m |miρmnhn| (27) と表される。全ての行列要素ρmn= hm|ˆρ|niは演算子ρˆを決定するために必要とされる。対角成分pn= ρnn はn個の光子を観測する確率である。 一方、コヒーレント状態で展開すると、式(8)のように、 ˆ ρ = Z Z hα0|ˆρ|α00i|α0ihα00|d 2α0d2α00 π2 (28) となる。しかし一般に、ρˆはコヒーレント状態で ˆ ρ = Z P (α)|αihα|d2α (29) とより簡単に表すことができる。ここで、P (α)はGlauber-SudarshanのP関数として知られている重みの 関数である。また、αの実部、虚部は位相空間の変数。ρˆがエルミート演算子であるときP (α)は実数である。 P (α)の規格化は、 T r ˆρ = T r Z P (α)|αihα|d2α =Z X n P (α)hn|αihα|nid2α = Z P (α)X n hα|nihn|αid2α = Z P (α)d2α = 1 (30) より得られる。よって、P (α)は位相空間の確率分布と考えられる。 しかし、ある量子状態においては、P (α)はこの確率分布とはかなり違った特性を持つことがある。例えば、 P (α)が負のときや1つの高いピークを持つ非古典的な量子状態*4を考える。 では、与えられたρˆについて実際にP (α)を求めていく。コヒーレント状態|ui、| − uiにおいて、式(29) より、 h−u|ˆρ|ui = Z P (α)hu|αihα|uid2α = Z
P (α)e−12|u|2−12|α|2−u∗α× e−12|α|2−12|u|2+α∗ud2α
= e−|u|2Z P (α)e−|α|2 eα∗u−αu∗ d2α (31) ここで複素数平面におけるフーリエ変換と逆変換は ½
g(u) =R f (α)eα∗u−αu∗
d2α f (α) = 1 π2 R g(u)eu∗α−uα∗ d2u (32) で与えられることに注意する。従って、 g(u) = e|u|2 h−u|ˆρ|ui (33) *4 P (α) ≥ 0 や、P (α) 6= δ(a − α) を古典的な量子状態とみなす。
ととると、そのフーリエ変換は f (α) = P (α)e−|α|2 を与える。よって式(32)より、 P (α) = e |α|2 π2 Z
e|u|2h−u|ˆρ|uieu∗α−uα∗d2u (34) が得られる。
以下の2つの例を考える。
例1
単一のコヒーレント状態|βi について考える。ここで、ρ = |βihβ|ˆ h−u|ˆρ|ui = h−u|βihβ|ui
= e−|β|2 e−|u|2 e−u∗β+uβ∗ (35) よって、 P (α) =e −|α|2 e−|β|2 π2 Z eu∗(α−β)−u(α∗−β∗) d2u ここで、積分の部分はちょうどディラックのデルタ関数の2次元形になっている。
δ2(α − β) = δ[Re(α) − Re(β)] δ[Im(α) − Im(β)]
= 1 π2 Z eu∗(α−β)−u(α∗−β∗)d2u (36) よって、 P (α) = δ2(α − β) (37) これは、古典の調和振動子の分布と等しい。ここで、もし古典的状態であったなら、数状態|niは、古典的に 表せなくなってしまう。 例2 単一の数状態|niについて、(ˆρ = |nihn|)
h−u|ˆρ|ui = h−u|nihn|ui = e−|u|2(−u∗u)n
n! (38) よって、 P (α) =e |α|2 n! 1 π2 Z (−u∗u)neu∗α−αu∗ d2u (39) この積分は普通の関数によって表せないので形式的に P (α) = e|α| 2 n! ∂2n ∂αn∂α∗n 1 π2 Z (−u∗u)neu∗α−αu∗ d2u =e |α|2 n! ∂2n ∂αn∂α∗nδ (2)(α) (40) と書く。このデルタ関数の導関数はデルタ関数よりも特異に振る舞い、積分の下でのみ意味を持っている。 例えば、ある関数F (α, α∗)について、 Z F (α, α∗) ∂2n ∂αn∂α∗nδ (2)(α)d2α = · ∂2nF (α, α∗) ∂αn∂α∗n ¸ α=0,α∗=0 (41)
ここで、光学の同等定理を紹介する。
今、演算子ˆa、ˆa†の正規関数Gˆ(N )(ˆa, ˆa†)を考える。ここで、消滅演算子ˆaは生成演算子ˆa†の右側に置く慣
用を用いることにすると、 ˆ G(N )(ˆa, ˆa†) =X n X m Cnm(ˆa†)nˆam (42) と表せる。この関数の平均は、 h ˆG(N )(ˆa, ˆa†)i = T r h ˆ G(N )(ˆa, ˆa†)ˆρ i = T r Z P (α)X n X m
Cnm(ˆa†)nˆam|αihα|d2α = Z P (α)X n X m
Cnmhα|(ˆa†)nˆam|αid2α = Z P (α)X n X m Cnmα∗nαmd2α = Z P (α)G(N )(α, α∗)d2α (43) 最後の式が光学の同等定理である。この定理は正規演算子の期待値がP関数に、演算子をˆa → α, ˆa†→ α∗ と置き換えて得られる関数の平均の重みをかけたものに等しいということである。 任意のˆa、ˆa†の関数O(ˆa, ˆa†)について、
: O(ˆa, ˆa†) :≡ O(N )(ˆa, ˆa†) (44)
と定義する。ここで、交換関係は無視する。数演算子n = ˆaˆaˆ †はすでに正規化されている。よって、
hˆni = hˆa†ˆai = Z
P (α)|α|2d2α (45)
ただし、nˆ2= ˆa†ˆaˆa†ˆaは規格化されていない。よって、
: ˆn2:= (ˆa†)2ˆa2 (46) とし、 h: ˆn2:i = h(ˆa†)2ˆa2i = Z P (α)|α|4d2α (47) 適した状態の下ではρˆに加えて他の演算子も表すことができる。これをP表示とよぶ。 ある演算子Bˆについて、P表示は ˆ B = Z Bp(α, α∗)|αihα|d2α (48) ˆ Bの平均は、 h ˆBi = T r( ˆB ˆρ) =X n hn| Z Bp(α, α∗)|αihα|ˆρ|nid2α = Z Bp(α, α∗)hα|ˆρ|αid2α (49)
密度演算子のコヒーレント状態での期待値は、位相空間の確率分布も表している。これは、Q関数や伏見関数 と呼ばれる。 Q(α) = hα|ˆρ|αi π (50) ˆ B = ˆIについて、規格化条件より、 Z Q(α)d2α = 1 (51) P関数とは違いQ関数は全ての量子状態において正である。コヒーレント状態の期待値として、演算子Bˆに 対応するQ表示を決定できる。 BQ(α, α∗) ≡ hα|B|αi = e−|α|2X n X m Bnm (n!m!)12 (α∗)n(α)m (52) ここでBnm= hn|B|miとし、再びh ˆBiを計算してみるが、ρˆをP表示で書くと、 h ˆBi = T r( ˆB ˆρ) = T r Z ˆ BP (α)|αihα|d2α =X n Z hn| ˆBP (α)|αihα|nid2α = Z P (α)hα| ˆB|αid2α = Z P (α)BQ(α, α∗)d2α (53) よって、もしρˆのP表示を使うとき、BˆのQ表示が必要となり、また式(49)より、BˆのP表示を使うとき ˆ ρのQ表示が必要となる。 Q関数は確率分布の性質を持っており、一方でP関数は半確率分布*5である。 実際、位相空間においては半確率分布があり、Weigner関数という。これは、任意の密度演算子ρˆにおいて、 W (q, p) ≡ 1 2π¯h Z ∞ −∞ hq +1 2x|ˆρ|q − 1 2xie ipx ¯ h dx (54) で定義される。ここで、|q ±12xiは位置の演算子の固有状態である。もし、状態が単一でρ = |ψihψ|ˆ ならば、 W (q, p) ≡ 1 2π¯h Z ∞ −∞ ψ∗(q −1 2x)ψ(q + 1 2x)e ipx ¯ h dx (55) ここで、hq +1 2x|ψi = ψ(q +12)である。 運動量について積分すると、 Z ∞ −∞ W (q, p)dp = 1 2π¯h Z ∞ −∞ ψ∗(q −1 2x)ψ(q + 1 2x) Z ∞ −∞ eipxh¯ dpdx = Z ∞ −∞ ψ∗(q −1 2x)ψ(q + 1 2x)δ(x)dx = ψ∗(q −1 2x)ψ(q + 1 2x) = |ψ(q)|2 (56) *5 見かけ上は確率分布のように見えるが、負の値をとるので正確に確率分布とは言えない
これは、位置の変数qでの確率密度である。同様にqで積分すると、 Z ∞ −∞ W (q, p)dq = |φ|2 (57) ここで、φは波動関数ψ(q)をフーリエ変換した運動量の平面における波動関数である。式(57)の右辺は、 運動量平面における確率密度である。ただし、W (q, p)自体は非古典的状態において負の値を持つときがある ので、真の確率分布とは言えない。
4
母関数
ここで、古典的なランダムな変数xについて考える。変数xの古典的な確率密度ρ(x)ˆ について、 ρ(x) ≥ 0 (58) と、 Z ρ(x) dx = 1 (59) を満たしているとする。xのn番目のモーメントを以下のように定義する。 hxni = Z dx xnρ(x) (60) モーメントhxniがすべてわかっているとき、ρ(x)ˆ は次の母関数を導入することによって表すことができる。 C(k) = heikxi = Z dxρ(x) = ∞ X n=0 (ik)n n! hx ni (61) 確率密度はこの母関数のフーリエ変換で与えられるので、 ρ(x) = 1 2π Z dke−ikxC(k) (62) 従って、仮に全てのモーメントhxniがわかっていたら、母関数C(k)がわかり、ρ(x)ˆ が導かれる。一方で、 母関数が与えられたら以下の式に従って、モーメントを求めることができる。 hxni = 1 in dnC(k) dkn ¯ ¯ ¯ ¯ k=0 (63) ここで、さらに量子力学における母関数を3つ導入する。 CW(λ) = T r[ˆρeλˆa†−λ∗ˆa] = T r[ˆρ ˆD(λ)] (Wigner) CN(λ) = T r[ˆρeλˆa†e−λ∗ˆa] (normally ordered) CA(λ) = T r[ˆρe−λˆa†e−λ∗ˆa] (antinormally ordered)(64) これらの関数は以下の関係がある。*6 CW(λ) = CN(λ)e− 1 2|λ|2= CA(λ)e12|λ|2 (65) *6 eA+ ˆˆ B= eAˆeBˆe−1 2[ ˆA, ˆB]= eBˆeAˆe12[ ˆA, ˆB]より示される
更に、次のことがわかる。
h(ˆa†)mˆani = T r[ˆρ(ˆa†)mˆan] = ∂
(m+n) ∂λm∂(−λ∗)nCN(λ) ¯ ¯ ¯ ¯ λ=0 h(ˆamˆa†)ni = T r[ˆρ( ˆamˆa†)n] = ∂(m+n)
∂λn∂(−λ∗)mCA(λ) ¯ ¯ ¯ ¯ λ=0 h{(ˆa†)mˆan}Wi = T r[ˆρ{(ˆa†)mˆan}W] = ∂(m+n)
∂λm∂(−λ∗)nCW(λ) ¯ ¯ ¯ ¯ λ=0 (66) 3つの母関数の代わりに、CahillとGlauberのパラメータsの関数を導入する。 C(λ, s) = T r[ˆρeλˆa†−λ∗ˆa+s|λ|2/2 ] (67) すると、 C(λ, 0) = CW(λ), C(λ, 1) = CN(λ), C(λ, −1) = CA(λ) (68) と、3つの関数が表せる。 母関数と前の節でみた半確率分布の間の関係をみていく。例えば、反正規の(antinormally)母関数につ いて、 CA(λ) = T r[ˆρe−λ∗ˆaeλˆa†] = T r[eλˆa†ρeˆ −λ∗ˆa] = 1 π Z d2αhα|eλˆa† ˆ ρe−λ∗ˆa |αi = Z d2αQ(α)eλα∗−λ∗α (69) と表せる。これは、Q関数の2次のフーリエ変換である。よって、逆のフーリエ変換をすると、 Q(α) = 1 π2 Z CA(λ)eλ∗α−λα∗d2λ (70) 次に正規の母関数について考える。式(29)より、P表現でρˆを表すと、 CN(λ) = T r[ˆρeλˆa† e−λ∗aˆ ] = Z P (α)hα|eλˆa†e−λ∗aˆ|αid2α = Z P (α)eλα−λ∗α∗d2α (71) となる。これは、P関数のフーリエ変換となる。よって、その逆は P (α) = 1 π2 Z CN(λ)eλ∗α−λα∗ d2λ (72) 最後に以上の二つの結果から、Wigner関数はWignerの母関数のフーリエ変換で示せる。 W (α) ≡ 1 π2 Z CW(λ)eλ∗α−λα∗ d2λ = 1 π2 Z CN(λ)e−|λ|22 eλ∗α−λα∗ d2λ (73)
母関数の応用として、P関数が熱状態や無秩序状態に対応していることを導く。まず、その場における以下 の密度演算子ρT hˆ で与えられる状態を思い出そう。 ˆ ρT h= 1 1 + ¯n ∞ X n=0 µ ¯ n 1 + ¯n ¶n |nihn| (74) ここで、n¯ は熱状態の平均値。 ¯ n = 1 exp( ¯hω kBT) − 1 (75) この密度演算子におけるQ関数は、 Q(α) = hα|ˆρT h|αi/π = 1 πe −|α|2X n X m hm|ˆρT h|ni(α∗)mαn (m!n!)1/2 = e −|α|2 π(1 + ¯n) X m µ ¯ n 1 + ¯n ¶n (α∗α)n n! = 1 π(1 + ¯n)exp µ − |α| 2 1 + ¯n ¶ (76) となる。次に、式(69)より CA(λ) = 1 π(1 + ¯n) Z d2αexp µ − |α| 2 1 + ¯n ¶ eλα∗−λ∗α (77) を得る。今、α = (q + ip)/√2,λ = (x + iy)/√2,d2α = dqdp/2とすると、 CA(x, y) = 1 2π(1 + ¯n) Z exp · −(q 2+ p2) 2(1 + ¯n) ¸ × e[i(yq−xp)]dqdp (78) となる。 Z e−as2 e±βsds = r π ae β2 4a (79) 上に示すガウス積分より、 CA(λ) = exp[−(1 + ¯n)|λ|2] (80) を得る。また、式(65)より、CN(λ) = CA(λ)e|λ| 2 となり、従って、式(72)より、最終的に以下を得るこ とができる。 P (α) = 1 α2 Z e−¯n|λ|2eλ∗α−λα∗d2λ = 1 π¯ne −|α|2¯n (81) これはガウス分布なので、真の確率分布として解釈しても無理がない。 最後に、コヒーレント状態(最も古典的な量子状態)と数状態(最も量子力学的な状態)におけるQ関数と Wigner関数について調べていく。コヒーレント状態(ˆρ = |βihβ|)において、Q関数は Q(α) = 1 π|hα|βi| 2= 1 πe −|α−β|2 (82)
となる。一方、数状態(ˆρ = |nihn|)では、 Q(α) = 1 π|hα|ni| 2= 1 πexp(−|α| 2)|α|2n n! (83) と表せる。2次元で描いてみると図3のようになり、コヒーレント状態におけるQ関数はちょうどβを軸と するガウス分布となる。 式(73)から、Wigner関数はコヒーレント状態のとき W (α) = 2 πe −2|α−β|2 (84) と得られる。また、数状態では W (α) = 2 π(−1) nLn(4|α|2)e−2|α|2 (85) ここで、 Ln(z) = 1 2πi I e−zt/(1−t) (1 − t)tn+1dt (Laguerre Polynomial) (86) 2次元で描いてみると(図4)、数状態における Wigner関数は負の値をとる。よって、Q関数は常に正なの で確率分布と言えるが、Wigner関数は確率分布とは言えないことがわかる。 図3 コヒーレント状態(β = 0)と数状態(n = 4)におけるQ関数(|α|にのみ依存) 図4 コヒーレント状態(β = 0)と数状態(n = 3)におけるWigner関数(|α|にのみ依存)