群論モデルにもとづく正方行列枠中の要素パターンに対する良さと複雑さ

DOI: http://doi.org/10.14947/psychono.36.4

群論モデルにもとづく正方行列枠中の

要素パターンに対する良さと複雑さ

濱 田 治 良

*・鍋 田 智 広

_{・福田T. スティーブ}

_・

内 海 千 種

・福 士 顥 士

・天 野   要

Goodness and complexity of dot patterns in a matrix

framework based on a group theoretical model

Jiro Hamada

*, Tomohiro Nabeta

, Steve T. Fukuda

,

Chigusa Uchiumi

, Kohji Fukushi

, and Kaname Amano

a _{Tokushima University,} b _{University of East Asia,} c _{Bunkyo University} d _{Kawamura Gakuen Women s University,} e _{Ehime University}

The group theoretical model of symmetry cognition （Hamada et al., 2016） was tested based on goodness and complexity judgments of dot patterns in a matrix framework. These patterns were divided into cyclic group patterns, determined by the number of rotations, and dihedral group patterns, determined by the number of reflection axes. The former have rotational symmetries and the latter reflectional and rotational symmetries. Undergraduates （N＝ 104） rated the goodness or complexity of 21-dot compound patterns. The goodness and simplicity of these patterns in both their original form and with partially expanded frameworks increased monotonously with the number of transformations. Partially expanding a pattern influenced the goodness of cyclic groups with one transformation, but not the goodness of dihedral groups. Partially expanding a pattern did have an effect on the complexity of both groups, but only with a large number of transformations. For patterns with 4 transformations, the goodness and sim-plicity of dihedral patterns were higher than those of cyclic group patterns. Furthermore, grouping effects influenced complexity but not goodness judgments.

Keywords: visual symmetry, pattern goodness and complexity, group theory, dot patterns, matrix framework,

grouping effects

は じ め に

要素パターンの良さと複雑さ 天野・今井（1992）は パターンの良さを群論的に検討し，Garner & Clement （1963）が考案した4本の鏡映軸，Imai （1972）が発案し

た2本の鏡映軸，そしてHamada & Ishihara （1988）が初

めて開発した 3本の鏡映軸を有するパターンを考察し た。次いで天野他（2001）は今井（1986）の変換構造説 を基礎として1次元白黒楕円パターン対の類似性につい て心理学的実験を行い，ハッセ図を導入して変換群構造 モデルを提案した。また小西他（2003）は変換群構造モ デルを再構成し，8要素白黒楕円パターンの良さに関す る今井（1986）の順序整合性と順序保存の仮説を確認し た。さらに天野他（2013）は8要素と12要素の白黒楕円 パターンにおいて要素数の増加に伴い空変換構造パター ンが激増するという困難を克服した。すなわち彼らは変 換群構造にハミング距離を導入して准変換群構造モデル を構成し，良さ判断のより詳細な順序性を明らかにし た。このようにパターンの認知判断は様々な側面で一貫 Copyright 2017. The Japanese Psychonomic Society. All rights reserved.

1 _{研究当初においてご指導を頂いた今井四郎北海道大}

学名誉教授と石原 徹徳島大学名誉教授に感謝いた します．また貴重なコメントを頂いた二名の査読者 に感謝いたします．

* Corresponding author. Tokushima University, Hachiman-cho, Babayama, Tokushima 770–8070, Japan. E-mail: jhamada@me.pikara.ne.jp

して群論に規定されている（濱田，1996）。そこで本研 究では群論にもとづいて正方行列枠に配置された要素パ ターンの良さと複雑さを検討する。 濱田・内海・福士・天野（2011a, 2011b）および濱田 （2014）は群論における位数（変換の個数）に着目して 9×9正方行列枠中の21要素複合パターンと19セル正六 角形枠中の充填パターンを用いて，良さと複雑さの評定 実験を行った。そして巡回群（Cyclic group: Cn）と二面 体群（Dihedral group: Dn）を区別して（n＝1, 2, 3, 4），パ ターン認知の3階層モデルを提案した。ここで整数nは 巡回群では不変性を示す回転の個数であり，二面体群で は鏡映軸の本数である。また群の位数は巡回群ではn， 二面体群では 2nである。ところで正方行列枠に関して Garner & Clement （1963）と今井・伊藤・伊藤（1976a）

らは3×3の枠組中の要素パターンの良さを検討したが， 各行各列に必ず要素が存在する5要素パターンという制 約の下では，この枠組にはD2とC4パターンが存在しな い。そこで本研究ではこれらのパターンを作成できるよ うに4×4と5×5枠組中の8要素と13要素からなる原型 パターン，そしてそれら2つの枠組を重ね合わせた9×9 と19×19枠組中の21要素複合パターンを考案して（濱 田他，2011a, 2011b; 濱田・内海・福士・天野，2013），良 さと複雑さの群論への依存性および群化の要因を検討す る。 翻って濱田他の3階層モデルでは群の位数には依存し ない第 1階層，次にCnとDnの位数への重みづけが同じ 第 2階層，最後にCnとDnの位数への重みづけが異なる 第3階層で良さと複雑さが決まるとしていた。簡潔に記 述すればすべての要素パターンの良さは第3階層で決ま る一方，複雑さはパターンの違いにより第1・第2・第3 階層で選択的に処理されているとした。しかしその後， Hamada et al. （2016）が濱田他（2013）のデータをt検定 で再検討すると，それまでは19セルを有する正六角形 枠中の非直線充填パターンの複雑さはすべて中程度であ り群の位数には依存しないとされていたことに反し，こ れらのパターンの複雑さが群の関与を受けていることが 判明した。たとえば平均値を Mとすると，Cnパターン （M＝5.1）よりDnパターン（M＝4.6）の方が単純だった （p＜.001）。つまり濱田他（2013）が用いた19セルを有 する正六角形枠中の充填パターンの良さと複雑さの位数 へ の依存性はそれと同じ枠組中の Hamada & Ishihara （1988）の非充填パターンの場合と一致した。そこで Hamada et al. （2016）は対称性認知の群論モデルを構成 した。ここで良さおよび単純さ（複雑さの逆）は Cnと Dnの位数に対して単調に増加し，正方行列と正六角形 の枠組を区別することが肝要である。すなわち正方行列 枠では良さと単純さは高い相関を示して同じ情報処理を 受け，Dnの位数がCnの位数より高く重みづけられると した（濱田他，2013［実験1］）。しかし19セルを有する 正六角形枠では良さはCnの位数がDnの位数より高く重 みづけられて決まるが，単純さ（複雑さの逆）は Cnと Dnの位数への重みづけは同じで，これらの認知判断は

異 な る 情 報 処 理 を受 け る と し た（Hamada & Ishihara, 1988［実験2］； 濱田他，2013［実験2］）。

van der Helm & Leeuwenberg （1996）および van der Helm （2014［第4章］）は，Palmer （1982, 1983）の変換モ デル（Transformational approach）とvan der Helmのホロ グラフィックモデル（Holographic approach）を比較検討 している。ホログラフィックモデルはパターン知覚を， 変換モデルはパターン認知を問題としている。パターン 知覚においては対称性の検出に必要な反応時間と正確さ を測定し（e.g., Bruce & Morgan, 1975; Wenderoth & Welsh, 1998），より速くより正確に検出されるパターンは良い とみなす。それに対してパターン認知は時間的制限がな い自由観察課題下で評定する要素パターンの良さと複雑 さそのものを扱う（e.g., 濱田他，2011b, 2013; Hamada et al., 2016）。ここで変換モデルは3次元的対象の心的操作 にもとづき，ホログラフィックモデルは1次元の文字列 （string）の形式化にもとづいていて，それらを2次元の 問題に適用している。 パターン認知については変換群のみならず枠組によっ て影 響 を 受 け る こ と が 知 ら れ て い る（Hamada et al., 2016）。たとえば濱田他（2013）によると，鏡映対称軸 の本数が同じ場合で正六角形枠の鏡映軸2本のパターン の良さ（D2: M＝5.7）は正方行列枠中の2本のパターン （D2: M＝7.5）より低く，枠組の違いが良さに影響してい ると考えられる（Hamada et al., 2016）。またvan der Helm & Leeuwenberg （1996［Figure 13］）では円形枠が，Palmer （1991［Figure 2］）と濱田他（2013［実験1］）では正方

行列枠が，そして濱田（1988［実験1］），Hamada & Ishi-hara （1988［実験2］）および濱田他（2013［実験2］）で は正六角形枠が使用されている。9×9正方行列枠の複

合パターンではD3パターンが，19セル正六角形枠では

D4パターンが存在しない。しかしvan der Helmの円形枠 ではどのような正多角形枠も実現でき，このような枠組 の違いが，良さにおける差異を引き起こしていると考え られる。そこで本研究では正方行列枠に限定して，巡回 群（Cn）と二面体群（Dn）の要素パターンに対する良さ と複雑さをより詳細に検討し群論モデルを考察する。 Hamada et al. （2016）はコントラスト極性と直線性の

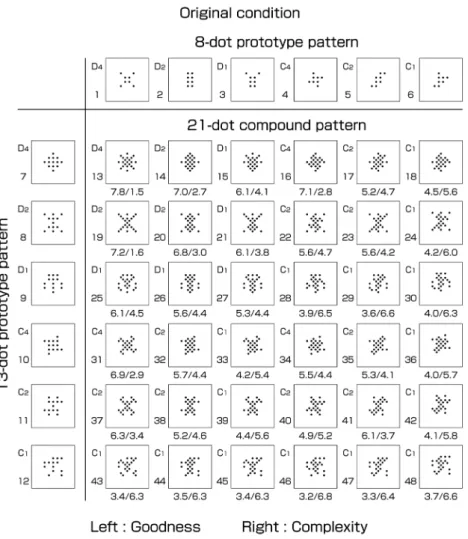
要因が良さでは弱いが，複雑さでは強く影響することを 示している。したがって群化の要因が要素パターンに対 する良さや複雑さに影響を及ぼしている可能性もある。 すなわちWertheimer （1923）はGestalt心理学における群 化の要因の1つとして近接の要因を指摘し，互いに近い 距離にある図がまとまることを明らかにしている。今 井・伊藤・伊藤（1976b）は1次元白黒楕円パターンに おいて複雑さは群化の程度を意味するラン数が多くな れば高まるが，良さはラン数の影響を受けないことを 明らかにした。また van der Helm & Leeuwenberg （1996 ［Figure 11D］）は反復パターンにおいて塊構造が増える と良さが増加することを示した。このようにラン数や塊 構造という群化効果が良さおよび複雑さに影響すること が知られている。さらに児玉・三浦（2011）は要素パ ターンを用いて知覚的体制化の仕方と良さ評定の関係を 検討した。そして知覚的体制化での群化数が少ないほど 良さが高まることを報告している。そこで本研究では群 化の要因を検討するために要素が広範囲に配置されたパ ターンを新たに採用する。 目 的 本研究では回転変換および鏡映変換に対して同じ不変 性を示すが，その形状が異なる基礎条件と拡大条件にお ける21要素複合パターンの良さおよび複雑さを測定し， 巡回群と二面体群の位数の効果を検討する。その際 13 要素原型パターン（Figure 1と2の番号7から12）を基 礎と拡大条件に共通して用いる。そして基礎条件では 4×4 枠組中の 8 要素原型パターン（Figure 1 の 1 から 6） を用いる一方，拡大条件では枠組を10×10に拡大した8 要素原型パターン（Figure 2の1から6）を設けて21要素 複合パターンを作成する。このようにして基礎と拡大条 件における21要素複合パターンの良さと複雑さを測定 する。また拡大条件において群化効果が良さと複雑さに 及ぼす影響を検討する。 方 法 刺激パターン 使用された刺激パターンは厚手の白紙（縦70 mm，横 66 mm）に描かれ，下端部中央にランダム数字 3 桁の カード番号が小さく印刷された。円形要素は黒色であ り，使用された全ての要素パターンが Figure 1と2に示 されている。そこにはDnとCnパターン（n＝1, 2, 4）の 違いと平均評定値が示されている。 基礎条件 基礎条件での要素パターン（以下，基礎パ ターンと略称する）の作成方法は濱田他（2011a, 2011b, 2013）と基本的に同じだったが，次に説明する拡大条件 のパターンが大きくなりすぎるので，要素の大きさと中 心間距離を半分にした。すなわち原型パターンにおける 要素の直径を 2 mm，その中心間距離を 5 mm とした。 Figure 1 の番号 7 から 9 に示されている 13 要素の Dn原 型パターン（n＝1, 2, 4）は5×5正方行列中に描かれ， それらは全て中央の列に 5 要素が配置された。一方， Figure 1の番号1から3に示されている8要素のDn原型基 礎パターン（n＝1, 2, 4）は4×4正方行列中に描かれ， それらは全て中央の4つの枡目に4要素が配置された。 次いで13要素と8要素Cn原型パターン（n＝1, 2, 4）は Dn原型パターンをもとにして，5×5と4×4正方行列の 最外周の4つの要素を右回りに一枡ずつ移動させて作成 した。このようにして菱形模様の 13要素D4パターン （番号7）と×形模様の8要素D4パターン（番号1）を風 車模様の C4パターン（番号 10と4）にした。その他の C2とC1原型パターン（Figure 1の番号11と12および番 号5と6）も同様にD2とD1原型パターンにもとづいて作 成した（濱田他，2011a）。 最後に21要素複合基礎パターンは5×5および4×4正 方行列の枠組の中心を一致させて2つの原型パターンを 重ね合わせて9×9正方行列枠中に描かれた。以上のよ うにして作成された36種類の複合パターンをFigure 1に 示す（番号13から48）。 拡大条件 拡大条件での要素パターン（以下，拡大パ ターンと略称する）の大きさについては，カードの大き さを基礎パターンと同一にするという実験的制約から 4×4 の枠組だけを 10×10 に拡大した。要素の直径は 2 mmであり，その中心間距離は13要素原型パターンが 5 mm, 8要素原型拡大パターンは15 mmであった。13要 素原型パターンは基礎パターンと同じであった（Figure 2の番号7から12）。一方，8要素原型拡大パターンでは 基礎パターンの各要素を中心から3倍の位置に拡大配置 した（Figure 2の番号1から6）。8要素原型拡大パターン と13要素原型パターンを重ね合わせた19×19正方行列 枠中の21要素複合拡大パターン36種類をFigure 2に示す （番号13から48）。 手続き 実験参加者は徳島大学学部生であり，実験は心理学授 業 の 一 環 と し て 実 施 さ れ た。 こ こ で 濱 田 他（2011a, 2011b, 2013）と同様に，実験終了後に各自のデータを用 いたレポート提出を義務づけた。教示と実験そしてレ ポート作成に約90分を要した。基礎パターン36枚と拡 大パターン36枚，合計で72枚の刺激パターンが各参加

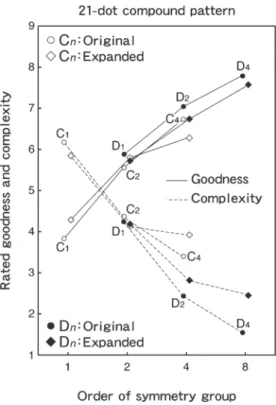
者に配布された。 参加者104名は良さを判断する52名，複雑さを判断す る52名にランダムに振り分けられた。また52名のうち 13名ずつがパターンの4方向（0°, 90°, 180°, 270°）に割 り当てられた。ただしこの 4方向は印刷上の方向であ り，各参加者が観察したカードの方向を統制できないの でランダム要因として扱い分析しなかった。評定は9段 階評定法（9が最良あるいは最も複雑，1が最悪あるい は最も単純）で行われた。教示文には1点から9点まで の尺度が図示され，それらの整数で評定することが求め られた。良さあるいは複雑さの評定基準は参加者の自由 な判断に委ねることが口頭で読み上げられた教示文で明 確に教示された。刺激パターンの概要を知るために，参 加者は評定に入る前にすべてのパターンを一通りランダ ム順で観察した。各評定の前に刺激パターンは充分に シャッフルされた。実験では刺激パターンの評定を自己 ペ ー ス で2 回 繰 り 返 し た。 こ の う ち 1 回 目 は 濱 田 他 （2011a, 2011b, 2013）と同様に練習試行として分析せず， 2回目の評定値を用いて分析した。反応用紙にはパター ン番号と評定値が刺激パターン毎に記入された。統計的 検定にあたってはSPSSのPASW Statistics 18を用いた。 結 果 基礎パターンおよび拡大パターンに対する良さと複雑 さの平均評定値をFigure 1と2に記されているパターン の下にそれぞれ示す。ここで左側の数値は良さ，右側の 数値は複雑さである。一方，Figure 3に群の位数の関 数としての良さ（実線）および複雑さ（点線）の平均評 定値を示す。ここでFigure 1と2に示されているように C1, C2, C4パターンはそれぞれ15 個，9 個，3 個であり， Figure 1. Results for the original condition. Means for goodness （left） and complexity （right） of the 36 21-dot compound

D1, D2, D4パターンはそれぞれ5 個，3 個，1 個である。 Figure 3によると良さと単純さ（複雑さの逆）は群の位 数に対して単調に増加している。 実験参加者内要因としての基礎条件と拡大条件 基礎と拡大パターン72個について良さと複雑さ間の Pearsonの相関係数を算出すると高い負の相関を示した （r＝−.955, p＜.001）。 CnとDn複合パターンの良さおよび複雑さ 良さにつ いて2 （基礎と拡大パターン）×3 （C1, C2, C4）の交互作用 （F（2, 102）＝8.497, p＜.001）と（C1, C2, C4）の主効果（F（2, 102）＝44.051, p＜.001）には有意差があったが，（基礎と 拡大パターン）の主効果（F（1, 51）＝.691, p＝.410）には 有意差がなかった。ここで交互作用が有意なのでC1パ ターンについて基礎と拡大パターンでの単純主効果を検 定すると（F（1, 51）＝4.985, p＜.05）で基礎より拡大パ ターンの方が有意に良かった。同様にC2パターンおよ びC4パターンについて基礎と拡大パターンでの単純主 効 果 を 検 定 す る と（F（1, 51）＝1.641, p＝.206） お よ び （F（1, 51）＝1.321, p＝.256）でいずれも良さに有意差はな かった。また2 （基礎と拡大パターン）×3 （D1, D2, D4）の 交互作用（F（2, 102）＝.411, p＝.664）と（基礎と拡大パ ターン）の主効果（F（1, 51）＝2.373, p＝.130）には有意 差 は な く，（D1, D2, D4） の 主 効 果（F（2, 102）＝50.603, p＜.001）には有意差があった。ここで回帰係数を算出 するとC1, C2, C4パターンに関して基礎パターン（1.347） の方が拡大パターン（1.004）より急峻である。またD1, D2, D4パターンに関して基礎パターン（0.960）と拡大パ ターン（0.921）はほぼ等しい。 複雑さについて 2 （基礎と拡大パターン）×3 （C1, C2, Figure 2. Results for the expanded condition. Means for goodness （left） and complexity （right） of the 36 21-dot compound

C4）の交互作用（F（2, 102）＝21.652, p＜.001）と（C1, C2, C4）の主効果（F（2, 102）＝190.403, p＜.001）には有意差 があったが，（基礎と拡大パターン）の主効果（F（1, 51） ＝.001, p＝.978）には有意差がなかった。ここで交互作 用が有意なので基礎パターンについてC1, C2, C4の単純主 効果を検定すると（F（2, 102）＝179.446, p＜001）で有意 差があり，Bonferroniの方法による多重比較ではすべて のペアに有意差があった（いずれもp＜.001）。同様に拡 大パターンについてC1, C2, C4の単純主効果を検定すると （F（2, 102）＝118.076, p＜001）であった。しかしC2とC4 には有意差がなく（p＝.206），その他のペアには有意差 があった（いずれも p＜.001）。またC1パターンおよび C2パターンについて基礎と拡大パターンの間で単純 主効果を検定すると（F（1, 51）＝1.660, p＝.203）および （F（1, 51）＝1.165, p＝.285）で有意差はなかった。さらに C4パターンについて基礎と拡大パターンの間で単純主 効果を検定すると（F（1, 51）＝5.288, p＜.05）で基礎より 拡大パターンの方が有意に複雑だった。一方，2 （基礎 と拡大パターン）×3 （D1, D2, D4）の交互作用（F（2, 102） ＝18.013, p＜.001），（基 礎 と 拡 大 パ タ ー ン） の 主 効 果 （F（1, 51）＝5.133, p＜.05），そして（D1, D2, D4）の主効果 （F（2, 102）＝114.332, p＜.001）にはすべて有意差があっ た。ここで交互作用が有意なので基礎パターンおよび 拡大パターンについてD1, D2, D4の単純主効果を検定す ると（F（2, 102）＝112.491, p＜001）および（F（2, 102）＝ 66.057, p＜001）でいずれも有意差があった。さらにD1, D2, D4の間における多重比較ではすべてのペアで有意差 があった（拡大パターンのD2とD4のみp＜.05で，その 他の拡大および基礎パターンはすべてp＜.001）。一方， D1パターンおよびD2パターンについて基礎と拡大パ ターンの間で単純主効果を検定すると（F（1, 51）＝.066, p＝.799）および（F（1, 51）＝3.001, p＝.089）でいずれも 有意差はなかった。しかしD4パターンでは（F（1, 51）＝ 19.876, p＜001）で基礎より拡大パターンの方が有意に複 雑だった。ここで回帰係数を算出するとC1, C2, C4パター ンに関して基礎パターン（−1.381）の方が拡大パターン （−0.969）より急峻である。またD1, D2, D4パターンに 関して基礎パターン（−1.346）の方が拡大パターン （−0.860）より急峻である。 同一の位数を有するDnとC2n複合パターン 良さに関 して位数2のパターンについて2 （基礎と拡大パターン） ×2 （C2, D1）の交互作用（F（1, 51）＝8.199, p＜.01）は有 意であり，（基礎と拡大パターン）の主効果（F（1, 51） ＝.045, p＝.834）， そ し て（C2, D1） の 主 効 果（F（1, 51） ＝.562, p＝.457）はいずれも有意差がなかった。また位 数 4 のパターンについて 2 （基礎と拡大パターン）×2 （C4, D2）の交互作用（F（1, 51）＝.160, p＝.691）および（基 礎と拡大パターン）の主効果（F（1, 51）＝2.432, p＝.125） に は有 意 差 が な く，（C4, D2） の 主 効 果（F（1, 51）＝ 11.477, p＝.001）には有意差があった。 複雑さに関して位数 2のパターンについて2 （基礎と 拡大パターン）×2 （C2, D1）の交互作用（F（1, 51）＝2.774, p＝.102）には有意差がなく，（基礎と拡大パターン）の 主効果（F（1, 51）＝.506, p＝.480），そして（C2, D1）の主 効果（F（1, 51）＝.022, p＝.882）はすべて有意差がなかっ た。また位数 4 のパターンについて 2 （基礎と拡大パ ターン）×2 （C4, D2）の交互作用（F（1, 51）＝.909, p＝.345） に は有 意 差 が な く，（基 礎 と 拡 大 パ タ ー ン） の 主 効 果（F（1, 51）＝4.666, p＜.05）および（C4, D2）の主効果 （F（1, 51）＝108.950, p＜.001）には有意差があった。 C1複合パターンにおける13要素C1原型パターンの効果 Figure 1の基礎条件と Figure 2の拡大条件において 13 要素のC1原型パターン（番号12）から構成されている 最下行の6種類の21要素C1複合パターン（番号で43, 44, 45, 46, 47, 48）を6行目C1パターンと略称する。そして Figure 3. Rated goodness and complexity as a function

合計で15個あるC1複合パターンの中で6行目C1パター ンを除く9種類の21要素C1複合パターン（番号で18, 24, 28, 29, 30, 33, 36, 39, 42）を非6行目C1パターンと略称す る。 良さ判断 Figure 1と2において2 （基礎と拡大パター ン）×2 （6 行目 C1と非 6 行目 C1パターン）の交互作用 （F（1, 51）＝8.812, p＜.01），（基礎と拡大パターン）の主 効果（F（1, 51）＝4.050, p＜.05），そして（6行目C1と非6 行目 C1パターン）の主効果（F（1, 51）＝42.713, p＜.001） にはすべて有意差があった。また6行目C1パターンにつ いて基礎と拡大パターンでの単純主効果を検定すると （F（1, 51）＝.025, p＝.874）で有意ではなかった。さらに 非6行目C1パターンについて基礎と拡大パターンでの単 純主効果を検定すると（F（1, 51）＝7.422, p＜.01）で有意 だった。ちなみに良さの平均値を記せば基礎の6行目C1 パターン（M＝3.4），基礎の非6行目C1パターン（M＝ 4.1），拡大の6行目C1パターン（M＝3.4），拡大の非6行 目C1パターン（M＝4.8）であった。 複雑さ判断 Figure 1 と 2 において 2 （基礎と拡大パ ターン）×2 （6行目C1と非6行目C1パターン）の交互作 用（F（1, 51）＝86.215, p＜.001）には有意差があり，（基 礎と拡大パターン）の主効果（F（1, 51）＝.338, p＝.563） には有意差がなく，（6行目C1と非 6 行目C1パターン） の主効果（F（1, 51）＝164.057, p＜.001）には有意差があっ た。また6行目C1パターンについて基礎と拡大パターン での単純主効果を検定すると（F（1, 51）＝17.486, p＜.001） で有意だった。さらに非6行目C1パターンについて基礎 と拡大パターンでの単純主効果を検定すると（F（1, 51） ＝26.446, p＝.001）で有意であった。ちなみに複雑さの 平均値を記せば基礎の6行目C1パターン（M＝6.5），基 礎の非 6行目C1パターン（M＝5.9），拡大の6行目C1パ ターン（M＝7.2），拡大の非6行目C1パターン（M＝4.9） であった。 そこでC1複合パターンの平均値についてまとめると， 良さではG （拡大の6行目C1パターン： 3.4）＝G （基礎の 6 行目 C1パターン： 3.4）＜G （基礎の非6 行目C1パター ン： 4.1）＜G （拡大の非6行目C1パターン： 4.8），複雑さ ではC （拡大の6行目C1パターン： 7.2）＞C （基礎の6行 目 C1パターン： 6.5）＞C （基礎の非 6 行目 C1パターン： 5.9）＞C （拡大の非 6 行目C1パターン： 4.9）の順序関係 が成り立っている。 8要素のD4原型パターンとC1原型パターンの置換の効果 良さ判断 Figure 1と2の複合パターンについて，1列 目には6つの13要素原型パターンに同一の8要素D4原型 パターンを重ね合わせた複合パターンの良さが示されて いる。また6列目には6つの13要素原型パターンに同一 の8要素C1原型パターンを重ね合わせた21要素C1複合 パターンの良さが示されている。その1列目によると良 さはD4, D2, D1複合パターンへと下降し，かつC4, C2, C1 複合パターンへと下降する傾向にある。ここで8要素D4 原型パターンを8要素C1原型パターンに置換すると，6 列目に示されているように6つのC1複合パターンの良さ は低下するが，1列目の順序関係が6列目において保存 されている。実際1列目と6列目間の良さについてPear-son の相関係数を算出すると基礎パターンは（r＝.878, p＜.05）で，拡大パターンは（r＝.919, p＜.01）だった。 これは濱田他（2011a, 2013）の結果の再確認となってい る。また良さについて1列目と6列目の平均値は基礎パ ターンが（M＝6.3とM＝4.1）であり，拡大パターンは （M＝6.0とM＝4.3）だった。そこで分散分析をすると2 （基礎と拡大パターン）×2 （1列目と6列目）の交互作用 （F（1, 51）＝3.873, p＝.055）および（基礎と拡大パターン） の主効果（F（1, 51）＝.019, p＝.891）には有意差がなく，（1 列目と 6列目）の主効果（F（1, 51）＝49.315, p＜.001）に は有意差があった。また 1列目について基礎と拡大パ ターンでの単純主効果を検定すると（F（1, 51）＝2.328, p＝.133）で有意でなかった。さらに6列目について基礎 と拡大パターンでの単純主効果を検定すると（F（1, 51） ＝.631, p＝.431）で有意でなかった。 複雑さ判断 Figure 1 と 2 の複合パターンについて， 良さ判断と同様に1列目と6列目の21要素複合パターン の複雑さを比較する。その 1列目によると複雑さはD4, D2, D1複合パターンへと上昇し，かつ C4, C2, C1複合パ ターンへと上昇する傾向にある。ここで8要素D4原型パ ターンを8要素C1原型パターンに置換すると，6列目に 示されているように6つのC1複合パターンの複雑さは上 昇するが，1列目の順序関係が6列目において保存され ている。すなわち1列目と6列目間の複雑さはPearsonの 相関係数は基礎パターンが（r＝.847, p＜.05）であり， 拡大パターンは（r＝.978, p＜.001）であった。これも濱 田他（2011b, 2013）の結果の再確認となっている。また 複雑さについて1列目と6列目を比較すると基礎パター ンは（M＝3.4とM＝6.0）で，拡大パターンは（M＝4.2 とM＝5.4）だった。そこで分散分析をすると 2 （基礎 と拡 大 パ タ ー ン）×2 （1 列 目 と 6 列 目） の 交 互 作 用 （F（1, 51）＝57.231, p＜.001）には有意差があり，（基礎と 拡大パターン）の主効果（F（1, 51）＝.399, p＝.531）には 有意差がなく，（1列目と6列目）の主効果（F（1, 51）＝ 354.243, p＜.001）には有意差が認められた。また1列目

について基礎と拡大パターンでの単純主効果を検定する と（F（1, 51）＝24.722, p＜.001で有意だった。さらに6列 目について基礎と拡大パターンでの単純主効果を検定す ると（F（1, 51）＝4.167, p＜.05）で有意だった。 考 察 対称変換群の位数への依存性 Palmerの変換モデルと van der Helmのホログラフィックモデルはパターンの良 さを扱っている。これに対して濱田他の群論モデルは良 さと単純さ（複雑さの逆）を同時に扱って（Hamada & Ishihara, 1988; Hamada et al., 2016）, Dnパ タ ー ン とCnパ

ターン（n＝1, 2, 4）の良さと単純さは二面体群と巡回群 の位数にしたがって単調に増加すると予測する。本実験 はこの予測を支持している。また濱田他（2011a, 2011b, 2013）とHamada et al. （2016）は正六角形枠中のDnパター ン（n＝1, 2, 3）の良さは正方行列枠中の Dnパターン （n＝1, 2, 4）の良さより低いことを示した。この実験結 果 は Palmer の 変 換 モ デ ル と van der Helm の ホ ロ グ ラ フィックモデルでは説明できないが，枠組を区別してい る群論モデルには矛盾しない。 Hamada et al. （2016）の群論モデルと同様に基礎と拡 大パターンの良さと単純さ（複雑さの逆）は群の位数に 対して単調に上昇した。この群論モデルは主に入力（パ ターン）と出力（良さ，単純さ）の関係を記述している が，Hamada et al. （2016）による正方行列枠の21要素複 合パターンでは二階層処理を受け，Hamada et al. （2016） とHamada & Ishihara （1988）の正六角形枠の充填・非充 填パターンでは三階層処理を受けていた。しかし本実験 では位数が同じであるDnおよびC2nについて分散分析す ると，良さと複雑さに共通してC2とD1には有意差がな く，C4とD2には有意差があった。換言すれば良さと単 純さ（複雑さの逆）は共にC4よりD2の方が高いにもか かわらず，C2とD1では同じである。この結果はHamada et al. （2016）の正方行列枠中の21要素白黒複合パターン で位数への重みづけは C2nよりDn （n＝1, 2）の方が高 かったことが部分的にしか，すなわち（n＝2）の場合に しか成り立たないことを意味する。 以上のようにこれらの実験結果に共通する処理特性は 要素パターンが提示されると，認知システムはまず不変 性の検出処理，すなわち群の位数の計数を行い，良さと 単純さは共に「群の位数に対して単調に上昇」する。こ の性質はHamada et al. （2016）で見出された正方行列枠 中の21要素白黒複合パターンおよび正六角形枠中の充 填・非充填パターンでも例外なく観察されている。した がってこの不変性の検出処理は認知システムの第一階層 で行われる。次いで認知システムは基礎と拡大パターン における枠組の違いや位数が 4 である C4およびD2パ ターンの違いを考慮して良さと単純さを出力する。 枠組の効果 9×9行列枠の基礎パターンと19×19行 列枠の拡大パターンの間でDnパターンでは良さの違い が認められなかったが（n＝1, 2, 4）, CnパターンではC1パ ターンのみ有意差が認められ位数が少ないときに枠組の 効果が現れている。一方，複雑さでは C4およびD4パ ターンのみで基礎と拡大パターンの間に有意差が認めら れ位数が多いときに枠組の効果が現れている。このよう に良さはC1パターンでは基礎より拡大パターンの方が 有意に高く，複雑さではC4およびD4パターンにおいて 基礎より拡大パターンの方が有意に高いと結論される。 拡大パターンにおける17要素の群化効果 Figure 1と 2において拡大の非6行目C1パターンは基礎の非6行目 C1パターンに比べてより良く，かつより単純だった。 この現象は，基礎の非 6行目C1パターンが21要素C1パ ターンとして一つに群化されるのに対して，拡大の非6 行目C1パターンでは中央部の17要素パターンがC1より 高次の構造を有する群化パターンであることに起因す る。すなわちこの17要素群化パターンの構造が特出し て良さを押し上げている。一方，基礎の6行目C1パター ンと拡大の6行目C1パターンの良さは一致していたのに 対して，前者は後者より単純だった。この現象は，今井 他（1976b）の良さと複雑さに対するラン数効果に類似 した効果が正方行列枠の要素パターンに生ずることを示 唆する。すなわち複雑さは拡大の6行目C1パターンが中 央部の17要素群化パターンと最外周の4要素パターンが 2 つに分離されて基礎の 6 行目 C1パターンより上昇す る。しかし良さにおいては，このような群化による分離 効果は生じないと説明できる。 Figure 2の拡大パターンの1 列目と6 列目間のPearson の相関係数は良さが（r＝.919）で複雑さが（r＝.978）と なり，良さおよび複雑さ共に Figure 1の基礎パターン （それぞれ r＝.878, r＝.847）より高い相関を示した。こ の高い相関は拡大パターンにおける1列目および6列目 にある中央部の17要素の群化パターンが全て同じであ ることに起因している。すなわち17要素群化パターン とその周辺の4要素が分離して認知されていることを示 している。そしてFigure 1と2において良さは1列目と6 列目に共通して基礎と拡大パターンに有意差はなかった が，複雑さには有意差があった。この現象も今井他 （1976b）が見出した群化による分離効果の存在を示唆し ている。一方，前述のごとく拡大パターンに関して最外 周4要素パターンがD4である1列目の良さの評定値はC4

である6 列目より有意に高く，複雑さは有意に低かっ た。この結果は17要素の群化パターンが同じである拡 大パターンにおいて，最外周4要素の構造が良さおよび 複雑さに対して依然として大きな影響を及ぼしているこ とを示している。 要約および結論 対称性認知の群論モデルを検証するために正方行列枠 の中に配置された要素パターンの良さと複雑さを測定し た。その際 4×4行列枠中の8要素と5×5行列枠中の13 要素からなる原型基礎パターンおよび10×10行列枠中 の8要素と5×5行列枠中の13要素からなる原型拡大パ ターンを用意した。そして2つの正方行列枠の中心を一 致させて重ね合わせて9×9および19×19の枠組で21要 素複合パターンを作成した。合計で104名の実験参加者 がこれらの要素パターンの良さあるいは複雑さを1から 9の整数で評定した。実験結果は以下の3点に要約され 結論づけられる。 良さと複雑さの位数への依存性 基礎および拡大パ ターンに対する良さと単純さはそれぞれ対称変換群の位 数の単調増加関数であると結論される。そして位数4の 基礎と拡大パターンの良さおよび単純さ（複雑さの逆） にはそれぞれ有意差があり，良さと単純さはいずれも C4よりD2の方が高い。 枠組の効果 36種類の21要素複合パターンについて Dnパターン（n＝1, 2, 4）および Cnパターン（n＝2, 4） では9×9行列枠中の基礎パターンと19×19行列枠中の 拡大パターンの間の良さには有意差がなく，C1パター ンのみに良さの有意差が認められた。そして複雑さにつ いては位数が高いC4およびD4パターンのみにおいて基 礎と拡大パターン間で有意差があった。 群化効果 拡大の非6行目C1パターンでは中央部の 17 要素パターンが C1より高次の構造を有する群化パ ターンであり，基礎の非6行目C1パターンでは全体が一 つの21要素C1パターンとして一つに群化されているの で，前者は後者より良くて単純である。そして基礎と拡 大の 6行目C1パターンの良さは一致していたのに対し て，前者は後者より単純だった。したがって複雑さは拡 大の 6行目C1パターンの17要素群化パターンと最外周 の4要素パターンが2つに分離されて基礎の6行目C1パ ターンより上昇するが，良さにおいてはこのような群化 による分離効果は生じないと結論される。 一方，拡大パターンにおける1列目および6列目にあ る中央部の17要素の群化パターンがすべて同じである。 したがって17要素群化パターンとその周辺の4要素が分 離して認知され，良さには1列目と6列目に共通して基 礎と拡大パターンに有意差はなかったが，複雑さには有 意差があり群化による分離効果が存在すると結論され る。 引用文献 天野 要・今井四郎（1992）．パターンの変換構造と良 さの認知に関する群論的研究 心理学研究，63, 181– 187. 天野 要・岡野 大・緒方秀教・芝田安裕・小西敏雄・ 福士顥士・濱田治良・今井四郎（2001）．パターンの 類似性判断に関する変換群構造説 情報処理学会論文 誌，42, 2733–2742. 天野 要・大矢拓也・荒木章太・長内 祐・遠藤慶一・ 岡野 大・小西敏雄・福士顥士・濱田治良（2013）． パターンの良さ判断に与える准変換群構造の効果 情 報処理学会論文誌，54, 2254–2264.

Bruce, V. G., & Morgan, M. J. (1975). Violations of symmetry and repetition in visual patterns. Perception, 4, 239–249. Garner, W. R., & Clement, D. E. (1963). Goodness of pattern

and pattern uncertainty. Journal of Verbal Learning and

Ver-bal Behavior, 2, 446–452. 濱田治良（1988）．パターンの複雑さと良さにおける対 称変換群の効果 心理学研究，59, 137–143. 濱田治良（1996）．反復模様の対称性と認知判断―並 進鏡映の普遍的効果と45°傾斜の選択的効果― 心 理学評論，39, 338–360. 濱田治良（2014）．パターン認知の 3 階層処理 徳島 大学渭水会々報第 43 号，16–21. Retrieved from http:// www.isuikai.jp （November 28, 2014）

Hamada, J., Amano, K., Fukuda, S. T., Uchiumi, C., Fukushi, K., & van der Helm, P. A. (2016). Group theoretical model of symmetry cognition. Acta Psychologica, 171, 128–137. http://dx.doi.org/10.1016/j.actpsy.2016.10.002

Hamada, J., & Ishihara, T. (1988). Complexity and goodness of dot patterns varying in symmetry. Psychological Research,

50, 155–161. 濱田治良・内海千種・福士顥士・天野 要（2011a）．対 称変換群に基づく複合図形の良さ 心理学研究，82, 1–8. 濱田治良・内海千種・福士顥士・天野 要（2011b）．対 称変換群に規定される円形要素図形の複雑さと良さ  心理学評論，54, 138–152. 濱田治良・内海千種・福士顥士・天野 要（2013）．知 覚の階層性に依存する複合図形と充填図形の良さと複 雑さ 基礎心理学研究，31, 123–134.

Imai, S. (1972). Effect of inter-pattern transformation struc-tures upon similarity judgments of linear pattern pairs.

Pro-ceedings of the 20th International Congress of Psychology,

164–165.

今井四郎（1986）．パターン認知の変換構造説 心理学 モノグラフ，No. 17. 東京大学出版会．

今井四郎・伊藤智啓・伊藤 進（1976a）．良さの判断に およぼすパターン内変換構造の効果 心理学研究，

47, 202–210. 今井四郎・伊藤 進・伊藤智啓（1976b）．パターンの良 さと複雑さの判断におよぼすパターン内変換構造とラ ン数の効果 心理学評論，19, 77–94. 児玉優子・三浦佳世（2011）．パターンのよさと知覚的 体制化 心理学研究，82, 277–282. 小西敏雄・岡野 大・緒方秀教・芝田安裕・天野 要・ 福士顥士・濱田治良・今井四郎（2003）．パターンの 良さ判断に関する変換群構造説 情報処理学会論文 誌，44, 2274–2283.

Palmer, S. E. (1982). Symmetry, transformation, and the struc-ture of perceptual systems. In J. Beck (Ed.), Organization

and representation in prtception (pp. 95–144). Hillsdale:

Erl-baum.

Palmer, S. E. (1983). The psychology of perceptual organiza-tion: A transformational approach. In J. Beck, B. Hope, & A. Rosenfeld (Eds.)，Human and machine vision (pp. 269– 339). New York: Academic Press.

Palmer, S. E. (1991). Goodness, Gestalt, groups, and Garner:

Local symmetry subgroups as a theory of figural goodness. In G. R. Lockhead & J. R. Pomerantz (Eds.), The perception

of structure: Essays in honor of Wender R. Garner (pp. 23–

39). Washington, DC: American Psychological Association. Wenderoth, P., & Welsh, S. (1998). Effects of pattern

orienta-tion and number of symmetry axes on the detecorienta-tion of mir-ror symmetry in dot and solid patters. Perception, 27, 965– 976.

Wertheimer, M. (1923). Untersuchungen zur Lehre von der Gestalt II. Psychologische Forschung, 4, 301–350.

van der Helm, P. A. (2014). Simplicity in vision: A

multidisci-plinary account of perceptual organization. New York:

Cam-bridge University Press.

van der Helm, P. A., & Leeuwenberg, E. L. J. (1996). Goodness of visual regularities: A nontransformation approach.

Psy-chological Review, 103, 429–456.