有向曲面, 非有向曲面のレベルつき写像類群のアーベル化について (離散群と双曲空間の複素解析とトポロジー)

(1)

有向曲面，非有向曲面のレベルつき写像類群のアーベル化について

岐阜大学教育学部佐藤正寿 Masatoshi Sato Faculty ofEducation, Gifu university

1

はじめに

本稿ではレベルつき写像類群のアーベル化について得られた結果_{[6], [16]} の要約を述べる．また，有向曲面のレベル4写像類群のアーベル化はまだ決定されていないが，これに関連して，最近調べたことについて述べる．第2節では [6] において得られた非有向曲面のレベル2写像類群のアーベル化の結果について述べる．第3節では，[16] において得られた，有向曲面のレベルつき写像類群のアーベル化の結果について述べる．また，[16] において，アーベル化の構造を調べる上で，曲面の $\mathbb{Z}$/2$\mathbb{Z}$係数1次ホモロジー群を基底とする自由加群からレベル 2写像類群のアーベル化への全射準同型を構成した．他のレベルの場合についても，全射とは限らないが同様の準同型を構成できる．本稿の第4節ではこの準同型に関連して，最近得られた結果について述べる．有向曲面と非有向曲面のレベル2写像類群のアーベル化には大きな違いがある。非有向曲面の場合には，レベル2写像類群上に代数的に構成された，mod2 Johnson準同型 ([3], [8], [13] 参照) という加群への準同型によって，そのアーベル化が完全に記述される．これに対し，有向曲面の場合にも mod2 Johnson 準同型は構成できるが，これはレベル

₂

写像類群のアーベル化に単射を誘導せず，アーベル化を記述するには不十分である．その理由は，有向曲面のTorelli群のアーベル化には幾何的な位数2の元が多く存在し，それらのmod2 Johnson準同型による値が$0$ になるためである．コホモロジー類の言葉では，この位数 2 の元は Birman-Craggs 準同型 ([2]) (もしくは，Torelli群の元による2つのハンドル体の貼り合わせにより得られる整ホモロジー 3 球面の_Rochlin不変量) に対応するものである．上で幾何的と述べたのはそのためである．筆者は，Heap [5] により構成された有向曲面の Torelli群上の加群への準同型と類似した準同型をレベル₂写像類群上に構成することにより，これらの元が1つを除いて，レベル ₂_{写像類群のアーベル化において非自明であることを示し，アーベル化を完全に決} 定した．現在筆者が興味をもっていることとして，$d$ が4の倍数のときの有向曲面のレベル $d$ 写像類群のアーベル化がある．これは完全には決定されておらず，原因は，上で述べた Torelli群のアーベル化にすむ位数 2 の元のうちの 1 つが，レベル$d$写像類群において消

(2)

えるかどうかがわかっていないためである．レベル₂_{写像類群については，第}₃_節で述べる，曲面の $\mathbb{Z}$/2$\mathbb{Z}$係数1次ホモロジー群の生成する自由加群からアーベル化への準同型を調べることで，このTorelli群のアーベル化にすむ位数2の元が消えることが偶然示せたため，アーベル化が完全に決定できた．なお，もしこの元がレベル$d$写像類群で生きているとすると，つまり，Torelli 群のアーベル化のレベル$d$写像類群による coinvariant (定義は 3 節で後述する) から，レベル$d$ 写像類群のアーベル化への準同型が単射だとすると，Torelli 群上で構成された Birman-Craggs 準同型を，レベル $d$写像類群上の準同型に拡張することができる．これに関連して，レベル$d$写像類群により 2 つのハンドル体を貼り合わせて得られる $\mathbb{Z}/d\mathbb{Z}-$ホモロジー ₃球面の Rochlin不変量をレベル$d$写像類群上の関数として表すことにも筆者は興味をもっている．

2

非有

$\prod p$

曲面のレベル

2 写像類群のアーベル化

廣瀬進氏との共同研究_[6] において得られた，非有向曲面のレベル2写像類群のアーベル化と生成系に関する結果について述べる．曲面$N_{g}$ を $\mathbb{R}P^{2}$ の$g$個の連結和として定め

る．曲面 $N_{g}$ の写像類群を，$\mathcal{M}(N_{g})=$ Diﬀ N $/($isotopy) として定める．以下では位数$d$

の巡回群を $\mathbb{Z}_{d}$ と表すことにする．写像類群$\mathcal{M}(N_{g})$ は曲面の $\mathbb{Z}_{2}$係数1次ホモロジー群

に作用するため，準同型$\mathcal{M}(N_{9})arrow AutH_{1}(N_{g};\mathbb{Z}_{2})$ が定まる．この準同型の核を $\Gamma_{2}(N_{g})$

と表し，レベル 2写像類群とよぶ．

写像類群$\mathcal{M}(N_{g})$ の有限生成系は Chillingworth [4], Birman-Chillingworth [1] におい

て与えられており，レベル2写像類群$\Gamma_{2}(N_{g})$ の有限生成系はSzepietowski [18] により

求められている．Szepietowski はまず，$Y$-homeomorphism と呼ばれる pushing map の

一種により，レベル2写像類群が正規生成されることを示した ([17]).

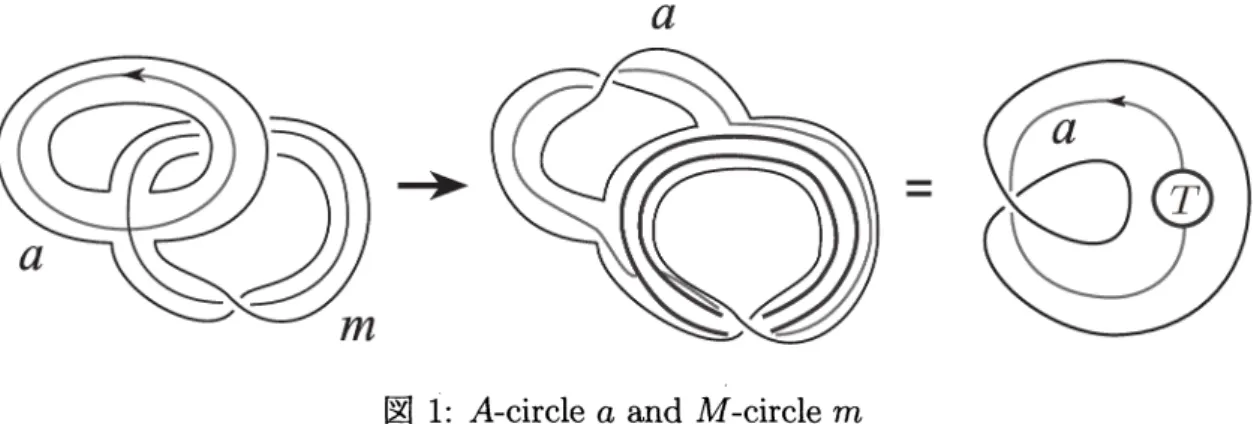
まず，$Y$-homeomorphism (もしくは，crosscap slide とも呼ばれる) について説明す

る．非有向曲面の単純閉曲線は 1 次 Stiefel-Whitney 類の値によって，その管状近傍がア

ニュラスになるか，メビウスの帯になるか，の2種類のものがある．これらをそれぞれ

A-circle, $M$-circle と呼ぶことにする．曲面$N_{g}$ 内の$A$-circle $a$ と $M$-circle $m$ が図 1 のよ

うに 1 点で交わっているとする．このとき $M$-circleの近傍$T$から，内部 (メビウスの帯)

を取り除くと境界は円周である．$A$_-circleと，この $M$-circle の近傍$T$ の境界は2点であ

り，$A$-circle と $N_{9}$ –Int$T$ の共通部分は，上の2点を端点にもつ弧であることに注意す

る．$Y$-homeomorphism _{$Y_{m,a}$} とは，右側の図にあるように，この弧に沿って $T$ を1周さ

せる写像として定義される．なお，中央の図では，$a$ の近傍を $m$ の近傍に沿ってハンド

ルスライドしている．

Szepietowski はさらに，有限個の $Y$-homeomorphism とDehn ツイストの2乗の生成

する部分群が正規であることを示し，$Y$-homeomorphismで正規生成される部分群，つま

(3)

$a$

図 1: A-circle $a$ and $M$-circle $m$

えた．廣瀬氏との研究では，Szepietowskiによるこの有限生成系の位数を小さくし，位数

$+(\begin{array}{l}g2\end{array})$ の生成系を構成した．

この生成系を説明する．曲面$N_{g}$ は$S^{2}$から $g$枚の開円板を取り除き，境界のそれぞれの

連結成分において，その対蹄点を同一視することにより得られる．これによって，図2の

ように曲面 $N_{g}$ を描くことにする．曲面$N_{g}$ 内の単純閉曲線として，図のように $\alpha_{i_{1},i_{2},\ldots,i_{k}}$

をとる．閉曲線 $\alpha_{i_{1},i_{2},\ldots,i_{k}}$ は $k$ が偶数のとき $A$-curve, $k$ が奇数のとき $m$-curveとなるこ

図2: simple closed

curve

$\alpha_{i_{1},i_{2},\ldots,i_{k}}$

とに注意する．我々の生成系は以下のものである．また，これはmod2 Johnson準同型

の像の $\mathbb{Z}_{2}$-rankに一致することがわかり，この生成系が最小位数のものであることを示

した．

定理2.1 ([6]). $g\geq 4$ とする．レベル2写像類群$\Gamma_{2}(N_{g})$ は以下の元で生成される．また，

これは最小位数の生成系である．

(i) $Y_{\alpha_{\iota},\alpha_{i,j}}$

for

$i\in\{1, . . . , g-1\},$ $j\in\{1, . _. _. _{, g\}$}, and $i\neq j,$

(ii) $T_{\alpha_{1,j,k,l}}^{2}$

for

$1<j<k<l.$

特に _{mod2 Johnson 準同型がアーベル化に単射を誘導することもわかり，アーベル化}

(4)

定理2.2 ([6]). $g\geq 4$ のとき， $H_{1}(\Gamma_{2}(N_{g}))\cong \mathbb{Z}_{2}^{(_{3}^{g})+(_{2}^{g})}.$

3

有

$\prod p$

曲面のレベル

_$d$

写像類群のアーベル化

次に，[16] において得られた，有向曲面のレベル$d$ 写像類群のアーベル化の結果を述べる．説明を簡単にするため，連結な境界をもつ種数$g$ の有向コンパクト曲面$\Sigma_{g,1}$ の写像類群

$\mathcal{M}_{g,1}=Diff_{+}(\Sigma_{g,1}, \partial\Sigma_{g,1})/($isotopy rel $\partial\Sigma_{g})$

の場合に述べる．筆者が決定したのは，$d=2$ と $d$ が奇数の場合におけるレベル $d$写像類群のアーベル化である．$d$が奇数のときのアーベル化は，Perron [13], Putman [14] においても独立に決定されている．また，$d=2$ の結果を拡張して，_Putman [15] は$d\equiv 2$ (mod4) のときのレベル$d$写像類群のアーベル化を決定している．$d$ が4の倍数のときには，Torelli 群のアーベル化にすむ1つの位数2の元が，レベル $d$写像類群のアーベル化において自明かどうかがわかっていないため，未解決である．有向曲面のレベル$d$写像類群のアーベル化を決定する上で，完全列

$1arrow \mathcal{I}_{g,1}arrow\Gamma_{d}(\Sigma_{g,1})arrow Sp[d]arrow 1.$

が重要である．ここで，$Sp[d]$ は symplectic群のレベル$d$ 主合同部分群である．

一般に群$G$ が加群$M$ に左から作用しているとき，coinvariant $M_{G}$ とは

ル$G= \frac{M}{\{gm-m\in M|g\in G,m\in M\}}$

で定義される加群である．上で述べた群の完全列はアーベル化の間に完全列

$H_{1}(\mathcal{I}_{g,1})_{Sp[d]}arrow H_{1}(\Gamma_{d}(\Sigma_{g,1}))arrow H_{1}(Sp[d])arrow 0$ (1)

を誘導する．ここで，$H_{1}(\mathcal{I}_{g,1})_{Sp[d]}$ は群$\Gamma_{d}(\Sigma_{g,1})$ の共役作用が誘導する，$H_{1}(\mathcal{I}_{g,1})$ への

SP

$[d]$ 作用の coinvariant である．以下では，$H_{d}=H_{1}(\Sigma_{g,1};\mathbb{Z}_{d})$ とおく．$H_{1}(\mathcal{I}_{g,1})$ の構造

は Johnson _[7] _{において求められており，特に coinvariant} は以下のようになる．

$H_{1}(\mathcal{I}_{g,1})_{Sp[d]}\cong\{\begin{array}{ll}\Lambda^{3}H_{d}\oplus \mathbb{Z}_{2}[Matrix]+[Matrix]+[Matrix], if d is even,\Lambda^{3}H_{d}, if d is odd.\end{array}$

ここで，$d$ が偶数のときに現れる位数 2 の元が，Birman-Craggs 準同型，もしくは，整ホ

モロジー ₃球面のRochlin不変量に由来する幾何的なものである．

また，$H_{1}(Sp[d])$ は[16] において決定されている．$d$が奇数のときは，[13], [14] におい

ても計算されている．$\mathbb{Z}_{d}$ を係数にもつ _$2g$次正方行列であって，$tAJ+JA=0$ を満たす

(5)

補題 3.1 ([16]). $g\geq 2$ とする．$d$ が奇数のとき，

$H_{1}(Sp[d])=\mathfrak{s}\mathfrak{p}(2g;\mathbb{Z}_{d})$

.

また，$d$が偶数のとき，

$0arrow H_{1}(\Sigma_{g_{)}1};\mathbb{Z}_{2})arrow H_{1}(Sp[d])arrow \mathfrak{s}\mathfrak{p}(2g;\mathbb{Z}_{d})arrow 0$ (2)

は完全であり，加群としては $H_{1}(Sp[d])=\mathbb{Z}_{d}\oplus \mathbb{Z}_{2d}(\begin{array}{l}2g2\end{array})(\begin{array}{l}2g1\end{array})$

3.1

$d$ が奇数のとき

完全列 ₍₁₎ _{と以上で述べてきたことから，}$d$が奇数のとき次の完全列が得られる

$\Lambda^{3}H_{d}arrow H_{1}(\Gamma_{d}(\Sigma_{g,1}))arrow \mathfrak{s}\mathfrak{p}(2g;\mathbb{Z}_{d})arrow 0.$

河澄 _[8] _{において，mod}dJohnson 準同型 $\tau_{1}:\Gamma_{d}(\Sigma_{g,1})arrow H_{d}^{\otimes 3}$ が構成されており，特に $d$ が奇数のとき，上の完全列の分裂を与えることがわかった．なお，Broaddus-Farb-Putman [3], Perron [13] も同種の準同型を独立に構成している．これにより，レベル$d$写像類群のアーベル化は以下のように表される．定理3.2 ([13], [14], [16]). $g\geq 4,$ $d$が奇数のとき， $H_{1}(\Gamma_{d}(\Sigma_{9,1}))=\Lambda^{3}H_{d}\oplus \mathfrak{s}\mathfrak{p}(2g;\mathbb{Z}_{d})$.

3.2

$d=2$ のとき次に，$d=2$のときを考える．$d$が奇数のときと同様に，mod2 Johnson準同型がレベル

2写像類群上に構成できるが，$H_{1}(\mathcal{I}_{g,1})_{Sp[d]}$ にはBirman-Craggs準同型に由来する $\mathbb{Z}_{2}$ 加

群があるため，これは完全列の分裂を与えるわけではなく，アーベル化を決定するのに

不十分である．代わりに，Heap[5] により構成された Torelli群上の準同型の $mod$$2$版と

よぶべきものを，レベル2写像類群上に構成することで，これが解決できた．これについ

て説明する．

写像類$[f]\in\Gamma_{2}(\Sigma_{g})$ について，有向閉3次元多様体$M_{[f]}$ を

$M_{[f]}=((\Sigma_{g,1}\cross[0,1])/(f(x), 0)\sim(x, 1))\cup(\partial\Sigma_{g,1}\cross D^{2})$

により定める．このとき，$H_{1}(M_{[f]};\mathbb{Z}_{2})\cong H_{1}(\Sigma_{g,1};\mathbb{Z}_{2})$ となる．また，多様体$M$ の spin

(6)

spin$M_{[f]}$ が存在する．したがって，以下では$M_{[f]}$ の 1 次コホモロジー群，および，spin構造は $\Sigma_{g,1}$ のものと同一視する．以上の準備の下，レベル2 写像類群から 3 次ボルディズム群$\Omega_{3}^{spin}(\mathbb{Z}_{2})$ への準同型写像を構成することができる．ここで，$\Omega_{3}^{spin}(\mathbb{Z}_{2})$ とは，3次元有向閉多様体_$M$, そのspin構造$\sigma,$ $\mathbb{Z}_{2}$ 係数 1 次コホモロジー類$c$の組のボルディズム類であり，あるコンパクト有向 4 次元多様体$V$ とその spin構造$\tau$ が存在して，

$\partial V=M_{1}\coprod(-M_{2}) , \tau|_{M_{i}}=\sigma_{i},$

さらに$H^{1}(V;\mathbb{Z}_{2})arrow H^{1}(M_{i};\mathbb{Z}_{2})$ による$c$の像が$c_{i}$であるとき，$[M_{1}, \sigma_{1}, c_{1}]=[M_{2}, \sigma_{2}, c_{2}]\in$

$\Omega_{3}^{spin}(\mathbb{Z}_{2})$ とみなすものである．なお，Brown不変量と呼ばれる，曲面の_$pin^{-}$ 構造の不変

量を通して，$\Omega_{3}^{spin}(\mathbb{Z}_{2})\cong \mathbb{Z}_{8}$ となることが知られている．

定理 3.3 ([16]). $g\geq 4$ とし，$\sigma\in$ spin$\Sigma_{g,1},$ $c\in H^{1}(\Sigma_{g,1};\mathbb{Z}_{2})$ とおく．写像

$\eta_{\sigma,c}:\Gamma_{2}(\Sigma_{g,1})arrow\Omega_{3}^{spin}(\mathbb{Z}_{2})$

を $\eta_{\sigma,c}(\varphi)=[M_{\varphi}, \sigma, c]$ と定めると準同型．また，

$\eta_{\sigma,c}$ が誘導する準同型

$\{(\eta_{\sigma,c})_{*}\}_{\sigma\in spin\Sigma_{g,1}}C\in H^{1}(\Sigma_{g,1;\mathbb{Z}_{2})}:H_{1}(\Gamma_{2}(\Sigma_{g,1}))arrow\Omega_{3}^{spin}(\mathbb{Z}_{2})^{N}$

は単射．ただしここで，$N$ は _spin$\Sigma_{g,1}$ と $H^{1}(\Sigma_{g,1};\mathbb{Z}_{2})$ の位数の積である．またさらに，

$H_{1}(\Gamma_{2}(\Sigma_{g,1}))=\mathbb{Z}_{8}(\begin{array}{l}2g1\end{array})\oplus \mathbb{Z}_{4}\oplus \mathbb{Z}_{2}.$

注意3.4. 特に完全列 (2) からわかるように， $Ker(H_{1}(\mathcal{I}_{g,1})_{Sp[2]}arrow H_{1}(\Gamma_{2}(\Sigma_{g,1})))=\mathbb{Z}/2\mathbb{Z}.$ したがって，Birman-Craggs 準同型の中には，準同型としてレベル2写像類群上に拡張しないものがあることがわかる．(実は，任意の2つのBirman-Craggs準同型の差は，上の準同型を用いてレベル2 写像類群上に拡張することがわかっている)

4

レベル $d$

写像類群のアーベル化における

Dehn

ツイスト

の $d$

乗

最後にレベル₄写像類群のアーベル化を調べるために，曲面の $\mathbb{Z}_{d}$係数1次ホモロジー群を基底とする自由加群からレベル $d$ 写像類群のアーベル化への準同型の性質を調べ

る．記号 $H_{d}^{prim}$ により，$H_{1}(\Sigma_{g};\mathbb{Z}_{d})$ の primitive な元 (言い換えれば，曲面を分割しない

(7)

補題 4.1 ([16]). 準同型 $\Phi_{d}$ : $\mathbb{Z}[H_{d}^{prim}]arrow H_{1}(\Gamma_{d}(\Sigma_{g,1}))$ を _{$\Phi_{d}([x])=[T_{x}^{d}]$} により定める

と，well-defined. ただし，$[x]$ は有向単純閉曲線$x\subset\Sigma_{g,1}$ の代表するホモロジー類とし，

$T_{x}\in \mathcal{M}(\Sigma_{g,1})$ は$x$ に沿う Dehnツイストとする．

証明．証明の概略を述べる．$H_{d}$ の元は有向単純閉曲線で代表できる．もし，$\Sigma_{g,1}$ 内の有

向閉曲線$x$,x’が$[x]=[x’]\in H_{1}(\Sigma_{9};\mathbb{Z}_{d})$ を満たすとする．このとき，[16, Lemma 6.2] に

書かれているように，ある写像類$\varphi\in\Gamma_{d}(\Sigma_{g,1})$ が存在して，$\varphi(x)=x’$. またよく知られ

ているように，写像類群において関係式$\varphi T_{x}\varphi^{-1}=T_{x’}$ が成り立つ．したがって，

$[T_{x}^{d},]=[\varphi T_{x}^{d}\varphi^{-1}]=[T_{x}^{d}]\in H_{1}(\Gamma_{d}(\Sigma_{g,1}))$

.

口

本節では，上で構成した準同型について次を示すことを目標とする．より精密に調べ

れば，レベル2 写像類群のときと同様に $Ker(H_{1}(\mathcal{I}_{g,1})_{Sp[d]}arrow H_{1}(\Gamma_{d}(\Sigma_{g,1})))$ が $\mathbb{Z}_{2}$ であ

ることを示せるかもしれないが，現状ではわかっていない $($なお，

$Ker(H_{1}(\mathcal{I}_{g,1})_{Sp[d]}arrow$ $H_{1}(\Gamma_{d}(\Sigma_{g,1})))=0$ or $\mathbb{Z}_{2}$ まではわかっている)

命題4.2. $x\subset\Sigma_{g,1}$ を曲面を分割しない単純閉曲線とする．

(i) $d\equiv 0mod 4$のとき，

$2d[T_{x}^{d}]=0\in H_{1}(\Gamma_{d}(\Sigma_{g,1}))$

.

(ii) $d\equiv 2mod 4$ のとき，

$4d[T_{x}^{d}]=0\in H_{1}(\Gamma_{d}(\Sigma_{g,1}))$

.

これを示すために，まず次の補題を示す．図 3: 補題 4.3. 図のように単純閉曲線$c_{1},$$c_{4},$$e_{1},$$e_{2}\subset\Sigma_{g,1}$ をとる．$d$ を 4 の倍数，かつ，正の数とする．このとき， $2[T_{c_{1}}^{d}]+2[T_{c4}^{d}]=[T_{e_{1}}^{d}]+[T_{e_{2}}^{d}].$

(8)

証明．簡単のため，曲線$c_{1},$$c_{2},$ $c_{3},$$c_{4},$$e_{1},$$e_{2},$$e_{3}$ に沿う Dehnツイストも $c_{1},$$c_{2},$$c_{3},$$c_{4},$$e_{1},$$e_{2},$$e_{3}$ と表す．このとき，Lantern関係式より， $c_{1}c_{2}c_{3}c_{4}e_{2}^{-1}=e_{3}e_{1}.$ $e_{3},$$c_{1)}c_{2},$$c_{3},$$c_{4}$ はすべて可換なので， $(c_{1}c_{2}c_{3}c_{4}e_{2}^{-1})^{d}=c_{1}^{d}c_{2}^{d}c_{3}^{d}c_{4}^{d}e_{2}^{-d}.$ また， $(e_{3}e_{1})^{d}=e_{3}(e_{1}e_{3}e_{1}^{-1})(e_{1}^{2}e_{3}e_{1}^{-2})\cdots(e_{1}^{d-1}e_{3}e_{1}^{-(d-1)})e_{1}^{d}.$ これより特に， $[c_{1}^{d}]+[c_{2}^{d}]+[c_{3}^{d}c_{4}^{d}]= \sum_{i=0}^{d-1}[e_{1}^{i}e_{3}e_{1}^{-i}]+[e_{1}^{d}]+[e_{2}^{d}].$ 曲面を分割する単純閉曲線に沿うDehnツイスト全体で生成される，写像類群$\mathcal{M}(\Sigma_{g,1})$

の部分群を $\mathcal{K}_{g,1}$ と表す．Johnson 核と呼ばれる部分群である．${\rm Im}(H_{1}(\mathcal{K}_{g,1})arrow H_{1}(\mathcal{I}_{g,1}))$

はレベル₂写像類群の共役作用で不変な $\mathbb{Z}_{2}$ 加群であることが知られている．いま $e_{3}$ は曲面を分割する単純閉曲線に沿うDehnツイストなので， $[e_{3}]=[e_{1}^{2}e_{3}e_{1}^{-2}]=\cdots[e_{3}^{d-2}e_{1}e_{3}^{-(d-2)}],$ $[e_{3}e_{1}e_{3}^{-1}]=[e_{3}^{3}e_{1}e_{3}^{-3}]=\cdots[e_{3}^{d-1}e_{1}e_{3}^{-(d-1)}].$ これより，$d$ が4の倍数のとき， $\sum_{i=0}^{d-1}[e_{1}^{i}e_{3}e_{1}^{-i}]=$ $O$

.

したがって，$[c_{1}^{d}]+[c_{2}^{d}]+[c_{3}^{d}c_{4}^{d}]=[e_{1}^{d}]+[e_{2}^{d}]$ を得る．$c_{3}c_{4}^{-1}\in \mathcal{I}_{g,1}$ であり，補題3.1の直前

で述べたように $H_{1}(\mathcal{I}_{g,1})_{Sp[d]}$ の位数は高々$d$なので，

$[c_{3}^{d}c_{4}^{d}]=d[c_{3}c_{4}^{-1}]+[c_{4}^{2d}]=2[c_{4}^{d}].$

また，$C_{1}=C_{2}\in \mathcal{M}(\Sigma_{g,1})$ より，$2[c_{1}^{d}]+2[c_{4}^{d}]=[e_{1}^{d}]+[e_{2}^{d}]$ を得る．口

命題 4.2 の証明．まず (i) を示す． $c_{1},$$c_{4}$ に適当に向きをいれ，その有向閉曲線が表す

ホモロジー類をそれぞれ $B_{1},$$B_{2}\in H_{1}(\Sigma_{g,1};\mathbb{Z}_{d})$ と表す．写像類$\varphi\in \mathcal{M}(\Sigma_{g,1})$ として，

$\varphi_{*}(B_{1})=B_{1}+B_{2},$$\varphi_{*}(B_{2})=B_{2}$ を満たすものをとる．補題4.3で得た式は$\Phi_{d}$ を用いて， $2\Phi_{d}(B_{1})+2\Phi_{d}(B_{2})=\Phi_{d}(B_{1}+B_{2})+\Phi_{d}(B_{1}-B_{2})$

と表せる．これに $k=0$, 1,

.

. ., $d-1$ 回 $\varphi$ を作用させると，

(9)

これより，$2d\Phi_{d}(B_{2})=0$

.

つまり，$2d[T_{c_{4}}^{d}]=0$が得られた．任意の2つの曲面を分割しな

い単純閉曲線は，ある写像類$\varphi\in \mathcal{M}(\Sigma_{g,1})$ で互いにうつり合うので，

$2d[T_{x}^{d}]=2d[\varphi T_{c_{4}}^{d}\varphi^{-1}]=\varphi_{*}(2d[T_{c}4]^{d})=0\in H_{1}(\Gamma_{d}(\Sigma_{g,1}))$

が得られる．

(ii) については，補題4.3を $d\equiv 2mod 4$ のときに調べることで，ほぼ同様に示すこと

ができる口

参考文献

[1] J. S. Birman and D. R. J. Chillingworth, Onthe homeotopy group of

a

non-orientable surface, Math. Proc. Camb. Phil. Soc. 71 (1972), 437-448. Erratum:

Math. Proc. Camb. Phil. Soc. 136 (2004), 441-441.

[2] J. S. Birman and R. Craggs, The $\mu$-invariant of3-manifolds and certain

struc-tural properties of the group of homeomorphisms of

a

closed, oriented 2-manifold,

Trans. Amer. Math.

Soc.

237

(1978),

283-309

[3] N. Broaddus, B. Farb, and A. Putman, Irreducible Sp-representations and

subgroup distortion in the mapping class group, Comment. Math. Helv. 86 (2011),

537-556.

[4] D. R. J. Chillingworth, A finite set of generators for the homeotopy group ofa

non-orientable surface, Math. Proc. Camb. Phil. Soc. 65 (1969), 409-430.

[5] A. Heap, Bordism invariants of the mapping class group, Topology 45 (2006),

851-886.

[6] S. Hirose and M. Sato, A minimal generating set of the level 2 mapping class

group of a non-orientable surface, arXiv preprint, 1306.5382.

[7] D. Johnson, The structure of the Torelli group III, Topology 24 (1985), 127-144.

[8] N. Kawazumi, Cohomological aspects of Magnus expansions, arXiv preprint,

math.$GT/0505497.$

[9] M. Korkmaz, First homology group of mapping class groups of nonorientable

surfaces, Math. Proc. Camb. Philos. Soc. 123 (1998), 487-499.

[10] W. B. R. Lickorish, Homeomorphisms of non-orientable two-manifolds, Math.

(10)

[11] W. B. R. Lickorish, On the homeomorphisms ofa non-orientablesurface, Math.

Proc. Camb. Philos. Soc. 61 (1965), 61-64.

[12] J. D. McCarthy and U. Pinkall, Representing homology

au-tomorphisms of nonorientable surfaces, ${\rm Max}$ Planck Inst. preprint

MPI/SFB85-11, revised version written on 26 Feb 2004 available from

http:$//www$

.

_math.msu._{$edu/\sim_{mccarthy}/publications/$}_selected.papers._html

[13] B. Perron, Filtration de Johnson et groupe de Torelli modulo$p,$ $p$premier, C.R.

Math. Acad. Sci. Paris 346

no.

11-12 (2008), 667-670.

[14] A. Putman, The abelianization of the level$L$mappingclass group, arXivpreprint,

0803.0539.

[15] A. Putman, The Picard group of the moduli spaceof

curves

with levelstructures,

Duke Math. J. 161 (2012),

no.

4,

623-674.

[16] M. Sato, The abelianization of the level $d$ mapping class group, J. Topology 3

no.4 (2010), 847-882.

[17] B. Szepietowski, Crosscap slides and the leve12 mapping classgroup ofa

nonori-entable surface, Geom. Dedicata 160 (2012), 169-183

[18] B. Szepietowski, A finite generating set for the leve12 mapping class group ofa