A Two-level Algorithm for Generating Multiset Permutations (Acceleration and Visualization of Computation for Enumeration Problems)

A

Two-level Algorithm

for

_{Generating Multiset Permutations}

Tadao Takaoka

Department of Computer Science,

University

of

Canterbury

Christchurch, New

Zealand

Email: tad

@cosc.canterbury.ac.nz

Abstract: Wepresent

an

algorithmthatgeneratesmultiset permutations in$O(1)$ tiine for each permutation, thatis, bya loop-less algorithm with$O(n)$ extramemoryrequirement. There already

exist several suchalgorithmsthatgeneratemultisetpermutations invarious orders. For multiset

permutations,

we

combine twoloop-less algorithms that

are

designedin the

same

principle oftree

traversal. _{Our order of generation is different fromanyexistingorder,andthealgorithmis} simpler andfasterthan theprevious

ones.

1. Introductlon.

$O(1)$ time generationforcombinatorial_objects,suchas_{permutations andcombinations, is known} alsoas loop-less algorithms. That is, given the currentobject,

we

generatethe next object

loop-lessly, e.g.,with

a

fmite nunber of statements. This is alsocalledcombinatorialGray code, since

the idea

is

a

generalizationofbinary Gray code to

more

general

combinatorial

objects. Ehrich [5]

was

thefirst to investigatethis topic. Since then

many

loop-lessalgorithms

were

inventedfor various objects, such

as

permutations, combinations, parenthesis strings, etc. To list

up

justa few,

see

Bitner, et al. [1],Ehrlich [5],Lehmer [11], Eadesand McKay[4], Chase [3] forcombinations,

Jolmson [7] andHeap[6] _{for pemiutations, Mikawa and Takaoka} [12], Vajnovszki[18], and

Walsh [20] for parenthesisstrings. We focus

on

the recent topic ofmultiset permutations inthis

paper.

Therehave beenseveral algorithms that generatemultiset permutations in0(1) timeper

permutation.

Canfield

and

Williamson

(1995) [2] and Korsh andLipschutz(1997) [9]

were

the firsttoinvestigate thisproblem. Theiralgorithms achieves $O(1)$ time,but

uses

a linkedlist

as a

containerofpermutations. Thus

we can

go from(1, 1, 1, 2, 2,2)to(2,2, 2, 1, 1, 1) in$O(1)$time bypointermanipulations. Since thesepapers, there

was

a

question whether

we

can

do thework

with only

arrays.

There

were

two solutions by Takaoka[16] andVajnovzski [19]. Bothrequire

O(kn) space apartfromthemain containerofpermutations, where$k$isthe numberofdistinct

items and$n$ is the sizeofpermutation. Thuswehave

a

question whetherwe

can

do theworkwith

only$O(n)$ extra

space.

Again

we

have two solutions _{byKorshand LaFollette (2004) [10] and} Takaoka and Violich(2005) [17].Those algorithms arebased

on

the two-level approach,which

we

use

in thispaperalso. In [9], theupperstructure is based

on

Johnson-Trotteralgorithmand the lowerstructureisbased

on

Eades andMcKay[4] forcombination generation.Theupperstructure for the latter method [17] is the same, Jolmson-Trotter,and the lowerisbasedonChase’s

algorithm forcombination generation.

Suppose

we

haveamulti-set$(1,\ldots,1,2,\ldots,2,\ldots\ldots k,\ldots,k)$,wherethere

are

_$n[i]$

items

of$i$, for

$i=1,$ _$\ldots,$$k$

.

Theupperalgorithm controls which item$i$ to move, and the loweralgorithm controls

themovementof those$n[i]$ identicalitemsbyregarding those

as ones

and others

as zeros.

Inthispaper,

we

use

Johnson-Trotterfor theupperstmcture andTakaoka’s algorithm[15] for

combinationgenerationforthelowerstructure,which

is

lessrestrictivethan Eades-McKay and Chase. Boththe

upper

stmctureand lower structure

are

based

on

the idea of tree traversal. Thus

our

algorithm has

a

more

transparent andconsistent design methodology and the

program

codeis

shorterthanexisting

ones.

To make theproblem

more

visible

we

startfrom

an

example. The

followingis thelistof permutations of(1,2,3, 4)byJohnson-Trotter,whichshouldbe read

1234 2134

2314

2341 3241 3214

3124

1324 1342 3142

3412

3421 4321 4312 4132 1432 1423 4123 4213 4231 2431 2413 2143 1243

Table 1. Permutations of(1, 2, 3, 4)by Jolmson-Trotter

Inthislist 1

moves

right

over

(2, 3, 4). Then

2

moves

right. Then

1

moves

left

over

(3; 2, 4), etc.,

altemately. Ifwe

remove

1 atthetop of eachcolumn,

we

havepermutations (2, 3,4), (3, 2,4), (3,

4, 2), (4,3, 2), (4,2, 3), (2, 4, 3). This list ofpermutations has

a

similarpattem ofthemovement

of 2 goingbackandforth altemately. Later

we

show

an

$O(1)$time algorithm for Johnson-Trotter.

Thenext listis the list of combinations of fouritems, called4-combinationsout of6$i$tems {1,

2, 3, 4, 5,

_6}

in in-place expressionandbinary vector form. Thebinary vector isforillustration

purposes.

In later sections,

we

generate onlyin-place forms. Incombination generation,

we

generatecombinations

one

by one,which

we

call the forward generation. When

we use

combination generationrepeatedly

as

the lowerstmctureofmultisetpermutation generation,

we

use

forward generation and backward generation altemately. Backward generation is to generate combinations in

reverse

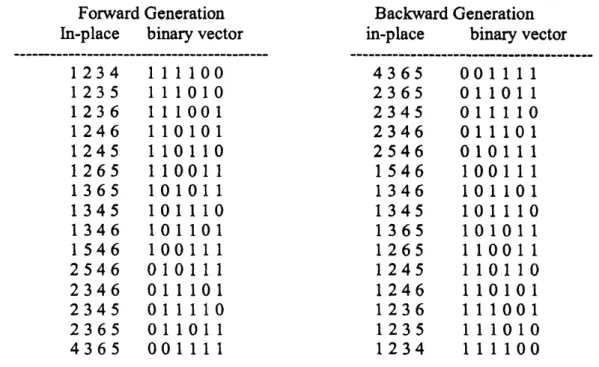
order offorward generation. Thisforwardgenerationisffom [15].

ForwardGeneration

In-place binary vector

1234 111100 1235 111010 1236 111001 1246 110101 1245 110110

1265

110011

1365 101011 1345 101110 1346 101101 1546 100111 2546

010111

2346 011101 2345 011110 2365 011011 4365 001111 BackwardGeneration

in-place binaryvector

$\overline{4365}$ 001111 2365 011011 2345 011110 2346 011101 2546 010111 1546 100111 1346 101101 1345 101110 1365 101011 1265 110011 1245 110110 1246 110101 1236 111001 1235 111010 1234 111100

Table 2. Listof4-combinations outofsix items

We note thatthere is only

one

changeRomcombinationto combination

in

the in-place list, and in

thebinaryvectorlist,

a

one moves over

a

blockof ones, and does notchange the relative order of

zeroes.

From 011110to011011, for example, the$4^{th}$element and $6^{th}$element

are

swapped, and

the$4^{th}$ element, 1, goes

over

the $5^{th}$element, 1. Ingeneral, the 1 may go

over

several consecutive

$1$’s in

a

larger example.Note alsothatfour

ones

atthe left end finally

come

to the right endof the

binaryvector, andvice

versa

forbackward generation. Chase does not havethisproperty. We

can

modi$\ddagger y$the algorithm

so

thatforward generation andbackwardgeneration altematetofit

Johnson-Trotter. The

source

code is givenin Appendix.

Suppose

we

have

a

list ofmultiset, such

as

(1, 1, 2, 2, 2, 3, 3, 4),

we move

$1$’sto the right

arrive attherightend,thatis, (2, 2, 2, 3, 3, 4, 1, 1),

we

perform

one

step ofthemovementof$2$’s

to theright,and $1$’s starttomove tothe left,

resulting in(1, 1, 2, 2, 3, 2, 3, 4). That is, the movement ofeachitem in Johnson-Trotter isgeneralized_{by the movements of severalidentical}

items

by

a

combinationgenerationalgorithm. InKorshandLaFollette [10], thecombination

algorithm is that of Eades and McKay, and in TakaokaandViolich [17], it

was

Chase’s algorithm.

The following isthe completelistofpermutations ofthemultiset(1, 1, 2, 2,3) in thispaper.

11223

23211 11322

12123

23121

13122

12213

23112

13212

12231 21132 13221 21231

21312

31221 21213 21321 31212

21123

12321

31122

22113

12312

32112

22131

12132

32121

22311

11232

32211

Table3. List ofpennutationsof(1, 1, 2, 2, 3)

2.General frameworkfor2-levelloop-less algorithms

Wehavetwokinds of2-level algorithms forcombinatorialgeneration. Let

array

$a$” bethemain

containerfor thecombinatorial objects,which

are

obtainedbycombiningupperandlowerobjects.

Type 1

1. Initializearray $a$”, the

upper

andlowerobjectsandotherdata structures

2.

repeat

3. repeat

4. computethenextlower object;

5. make

an

effect

on

the objectin array $a$”

6. untillast lower object

7. re-initializationfor lower objects 8. compute thenextupperobject;

9. until lastupperobject

Example [17] Mixedparenthesis strings

are

describedbriefly. Upper objects

are

well-formed

parenthesisstrings. Lower objects

are

the setof binary strings in Gray code. Theupperalgorithm takes

care

oftheparenthesis strings, whiletheloweralgorithmcarriesoutthechanges of

parentheses andbrackets driven by the binary strings inGray code. The central algorithmic issue

hereisthe computation ofpositions of changesbetweenparentheses andbrackets. At line 7,

we

cannotaffordto spend

more

than0(1) time,meaning

we

needto generatebinary strings

repeatedly

or

reversely. Lower Upper $00$ _{$()()$ $(())$} $01$ _{$()[]$ $[()]$} 11 $[][]$ $[[]]$ 10 $[]()$ $([])$

Type 2.

1. Initializearray $a$”and other data stmctures. Let$i$be current

upper

object

2. repeat

3. compute thenextlowerobject for

upper

object $i$

4. make

an

effecton the object inarray $a$”

5. if last lowerobjectthen begln

6. re-initializationfor lower objects for$i$

7. computethenext

upper

object andlet it be the current$i$

8. end

9. until lastupperobjecthasbeenprocessed

We

use

type 2formultisetpermutations. Upper objects

are

permutations (specifically, moving

items) byJohnson-Trotterand the lower objects

are

combinationsofitems $i$

.

3. General FormofLoop-less Algorithmsby Tree Traversal

Weborrow

some

materials ffom [15] to describe the concept oftree traversal usedinthis

paper.

Let$\Sigma=\{\sigma_{0}, \ldots , \sigma_{r\cdot 1}\}$ be

an

alphabet forcombinatorial objects.Acombinatorial objectis

a

string

$a_{1}\ldots a_{n}$of length$n$suchthat each $a_{i}$is taken ffom$\Sigma$ andsatisfies

some

property. Anorder is

defined

on

$\Sigma$ with_{$\sigma_{i}<\sigma_{i+1}$}

.

Let$\Sigma^{n}$be thesetofallpossiblestrings

on

$\Sigma$ oflength

$n$withthe

lexicographic order$<$

.

The order $<$

on

aset ofcombinatorialobjects, $S\subseteq\Sigma^{11}$, is definedby

projectingthe lexicographic order

on

$\Sigma^{\mathfrak{n}}$ onto S.

Thelexicographictree,

or

lexico-treefor short, of$S$ is definedinthe followingway. Each $a\in S$corresponds to

a

path from the_{root to}

a

leaf. The_root is_atleve10. _{If$a=a_{1}\ldots a_{n},$}$a_{i}$

corresponds to

a

nodeat level$i$

.

We referto

$a_{i}$

as

thelabel forthe node. Wesometimes do not

distinguish between node andlabel. Ifa and$b$ share the

same

prefix oflength$k$,theyshare the

pathoflength$k$inthe tree. The children ofeachnode

are

ordered accordingto the labelsofthe

children. A path from the root to

a

leaf corresponds to aleafitself,

so

acorresponds to aleaf. The combinatorial objects attheleavesare thusordered in lexicographic order

on

S.

The twistedlexicotree of

a

set $S$ of combinatorial objectsis defined

as

follows together with

theparityhnction. Weproceed to twist

a

givenlexico-treeffom theroottoleavesin

a

breadth-first search

manner.

Letthe parity ofthe rootbeeven. Supposeweprocesseduptothe i-thlevel.

If the parity ofanode$v$atlevel$i$ is even,we do nottwistthebranchesffom

$v$ toits children. If

theparity of$v$ isodd,

we

arrangethe children of$v$in

reverse

order. Ifweprocess all nodes at

level$i$,

we

give parity to all thenodesatlevel_$i+1$ from first to lastaltemately

starting from

even.

We denote the parityofnode$v$byparity(v).When

we

process nodes atlevel$i$

in

thefollowing

algorithms, which

are

children of

a

node $v$ suchthatparity(v)_$=p$,

we

saythe currentparityoflevel $i$ is

$p$. Note that (labels of)nodesatlevel$i$

are

inincreasing order if the parity of theparentif even,

orequivalentlyifthe currentparityoflevel $i$is

even.

If theparity is odd, theyare in decreasing

order. We draw trees lying horizontallyfornotational convenience. We refertothe topchild of

a

node asthe first child and the bottom

as

the last child.

Ifthe labelsonthe paths from the root to two adjacent leavesinthetwisted lexico-treefor$S$

are

differentat

a

fixed number ofnodes,

we

can

generate $S$ fromobject to object with the fixed

number ofchanges. Wedesign

an

efficient algorithm thattraverses thetwistedlexico-tree and generatecombinatorial objectsin$O(1)$time

per

object. Thus the fixed number of changes is a

necessary

condition for

our

algorithm,butnotsufficient.

The currentparityatlevel$i$ is givenbyparity_$[i]$, andtheprocedure”output”is onlyto

see

theresult; for$O(1)$time this will be

eliminated.

We allow$O(n)$time forinitialization,but for the repeated

use

ofgenerationcamotaffordto re-initialize

arrays

in$O(n)$ time. This willbe

addressed in latersections. Theparity$0$ is for

even

and 1 for odd. Let$\Sigma=\{0, \ldots,r- 1\}$

.

We

Traversal fromanodetothenextsiblingnodecorrespondsto generating thenextobject, making

some

changes

on

theobject. Wemaintain theparityinformationfor eachlevel in array“parity”.

Thelevel of thetree corresponds tovarious aspectsof the objects

as we

will

see

inlatersections. A genericformof the algorithm follows. All algoritluns

are

givenin Pascal style pseudocode. Algorithm 1. Iterativetree traversal inpseudocode. $i$keeps track of thecurrent levelofthe

tree. 1.

initialize

array

ato be the first objectin$S$;

2. initialize$v_{1},$ _$\ldots,$ $v_{n}$tobe nodes

on

thepath to thefirst object(toppath);

3, _for$i;=0$ to$n$do $up[i];=i$;

4. for$i;=0$ _to$n$do$parity[i]:=0$;

5. repeat 6. output(a);

7.

$i:=up[n];up[n]:=n$;

8. performchanges

_{on a}

at$v_{i}$ and related positions;

9. let$v_{i}$ gotothenextnode atlevel$i$based

on

the currentparity;

10. $ifv_{i}$ is the last child ofitsparentthen begin

11, _let$v_{i}$ further gotothe next node atlevel$i$;

12. up$[i];=up[i- 1]$;up$[i- 1];=i- 1$;

13. parity[i]:$=1$-parity[i]

14.

end

15. untll$i=0$

.

When

we come

tothe last child of

a

parent($w$inthe abovefigure),

we

haveto updateup$[i]$ to up[i-l]

so

that when

we

visit the last leafofthe sub-treerooted at$w$,we

can come

backdirectly

ffomtheleaf to$w$

or

its ancestorifwitselfis a lastchild. We referto thepathsfrom$v_{i}$to a and

from next$v_{i}$to $a$’

as

the current pathandthe oppositepath. A current path and opposite path

consist oflastchildren andfirst childrenrespectively except forthe left ends. Ifnext$v_{i}$inthe

abovefgure is

a

lastchild,

we

fiirther set$v_{i}$ tothe nextnode ofnext$v_{i}$, say$u$,

so

we can

avoid

$0(n)$ time_{to set}up the environment_{for such}$u$’s later. This isillustratedinthe above figure bythe

path from “next$v_{i}$ ”

to “next object$a$’ ”. That is, when

we

traversedown the currentpath, we

prepare

for the opposite path

so

that

we

can

jump

over

the opposite path from level$i$totheleaf.

In thissituation

a

and$a$’ sharethe

same

prefixfromposition 1 toi-l. We call$i$thedifference

point. The two strings also sharethe

same

suffix(possibly empty). Letthe longest such is from

positionj$+1$ to$n$

.

Then

we

callj thesolutionpoint. Inmitively this is the point where the

difference causedupstreamis solved. Algorithms for permutations and for combinations inthis

paper

are

designed along the paradigm in this section.

4. Review ofJohnson-Trotter

In theiterative algorithmforJohmson-Trotter,thelevelof the tree corresponds to the item

we are

trying to

move.

Paritycorresponds tothedirectionofmovement, left

or

right, represented by-l

(oddparity)

or

$+1$ (evenparity). Array $p$

” is

to hold theposition of

item

$x$

.

Array element $c[i]$”

is to count thenumber of nodesatlevel$i$ and check the lastchildcondition. Procedure“move(x)”

is tomove item$x$to thedirection givenby $d[x]$, andupdate the positions of affected items. The

comment$/*$output$*/$ shows the point where a

new

permutationis generated. Array $d$”playsthe

role ofparityin Algorithm 1. Inthe

program,

levelvariable $i$corresponds to item $i$

.

If

we

regard

the position of eachitem as the labelof thenode,

we

have aclose correspondencewiththe twistedlexico-tree. In the following figure, level numbers arereversedto allowitem

moves

first.

leve14

leve13

level.2

level 1

move(1)

1234

move(l)

2134

move(l)

2314

2341

move(l)

3241

move(l)

3214

move$(i)$

3124

1324

move(l) move(l)

1342

3142

move(l)

3412

3421

move(1)

₄₃₂₁

move(l)

4312

move(l)

4132

1432

move(l)

₁₄₂₃

move(l)

4123

move(1)

₄₂₁₃

4231

move(l)

2431

move(1)

₂₄₁₃

2143

move(l)

1243

Figure

1

Tree forJohnson-Trotter

Inthis figure levels increasefrom leaves totheroot.Variable $i$keeps trackofthe currentlevelof

treetraversal. The actionmove(x)is attachedto each node ofthetree. Variable $c[i]$ is called the childcounter, which

can

tell if

we

are

hitting

a

last child at the current level. In the following sections,

we

say$x$

moves

actively in the procedure call “move(x)”,and theitemneighboring$x$

moves

passively by swapping.

Algorithm 2. Iterativealgorithm for Johnson-Trotter

proceduremove(x);

begin

var

$w$;

$w;=a[p[x]+d[x]];a[p[x]+d[x]];=x;a[p[x]]:=w$;

$p[w]:=p[x];p[x]:=p[x]+d[x];c[i]:=c[i]+1;/*$ output $*/$

end;

for$i:=1$ to$n$ do begin $a[i]:=i,$_{$up[i];=i;p[i]:=i;c[i]:=1;d[i];=1$}; end; repeat $i:=up[1]$;up$[1]:=1$; move(i);

if$c[i]=n- i+1$ _{then begin} $/*$ currentlyhitting

a

last childat level $i^{*}/$

up$[i];=up[i+1]$;up$[i];=i+1;/*$ inherit theup-value of the parent $*/$

$c[i];=1$;

$d[i]:=- d[i]$; $/*$ parity(direction)reversed $*/$

end until$i=n$;

end.

5. The TwoLevelApproach

Now

we

combinethe loop-lessalgoritluninSection4 forpermutationsand the combination generation algorithm describedlaterinthenextsection in detail. Let

us

generatepermutations of

multiset$(1,1,\ldots,1,2,2,\ldots,2,\ldots,k,k,\ldots,k)$

.

Let$n[i]$ be thenumberofitems $i$inthemultiset,that is,

themultiplicityof$i$

.

Let$n=n[1]+\ldots+n[k]$, that is, the total

sizeof the multiset.

Whenitems 1

move

in the container

array

$a[1..n]$, the rangeofmovement is $[$1..$n]$,the

wholespanofarray $a$”. The rangeofitems 2 is limitedto $[1.. n- n[1]]$when all ls

are

atthe right

end,

or

range $[n[1]+1..n]$ if all ls

are

attheleft end. If

we

defme the capsule of2 as

range

$[1.. n- n[1]]$,the latter

range

_{of the capsule}

can

_{be obtained by adding thebase, base}$[2]=n[1]$

.

_In

general,

we

move

itemj in the capsule [1.. size$[i]$] bycombination generation where size$[i]$ isthe

size ofthe capsule. The capsule is activatedbyperformingonestep ofcombination generation, whenall loweritems

are

tothe left

or

tothe right, thatis, outsideofit.Note thatwhenwetalk aboutmovementbyswapping twoitems,

we

mean

active movementoftheloweritem, not

passivemovementof thehigher item. Thusitems $k$

never move

actively. Theabsolute

range

of

a

capsuleisobtained by adding base$[i]$ to it. The values ofsize$[i]$andbase$[i]$ foritem $i$

are

defined

as

follows:

size$[i]=n[i]+\ldots+n[k],$ $i=1,$ $\ldots$, k-l

base$[i]=$the number of all loweritems_{totheleft of}any

occurrence

_ofitem$i$

Thecomputationofbase[i] will beexplained later. Wemaintain positions ofitems $i$by the

combination generation algorithm. Suppose the positions ofitems $i$changed from$(q[1],$

$\ldots,$ $q[|]$,

..., $q[n[i]])$_to$(q[1], \ldots, q’ lj], \ldots, q[n[i]])$ inthe capsule by thecombinationgeneration algorithm.

Then

we see

that

an

item$i$

moves

Romposition_$qD$] toposition_$q’[|]$ inthe capsule ofitem $i$ inthe

main container

array

$a$”. In Algoritlun 4, those values of$q[\int]$and$q’[|]$

are

retumedbythe call to

“combination-server” inglobal variables “from”and“to”. Thevalues of “from”and “to”

are

adjusted byadding base$[i]$to the positions in therange. Let_{$C(n[i], n)$}be the binomial coefficient of$n[i]$-combinationsoutofn items.

Example. Suppose the firstitem of 2 moved right from(1,1,1,3,2,2,3) to (1,1,1,3,3,2,2). Since $2s$

are

movingright globally, thepositions of$2s$before andafterthe

move are

$($5, $6)=3+(2,3)$ and $($7, $6)=3+(4,3)$, modified by adding the base 3 to 2-combinations, (2,3)and(4,3) out of4 items

{1, $\ldots$ ,

4}.

Thus2

moves

fromposition 5 to7.

Inthefollowing, the work “maintaincombinations”

includes

”retumthenextcombination”.For

Algorithm

3.

Multiset Permutation

Generation

Lower Level

Combination-server $/*$ This seiver performs the following operations

on

demand $*/$

begin

Initialize$n[1]$-combinationsout ofsize[l] items

Initialize $n[2]$-combinations out ofsize[2] items

Initialize $n[k- 1]$-combinations out ofsize[k-l] items

Maintain$n[1]$-combinationsoutofsize[l] items

Maintain$n[2]$-combinations outofsize[2] items

Maintain$n[k- 1]$-combinationsoutofsize[k-l] items end

Upper Level

procedure move(x);

begIn

var

$w$;

$c[i];=c[i]+1$;

Let thechangeofcombinationbefrom “from” to“to”; from:$=ffom+$ base$[i]$; to:$\neg-0+$base$[i]$;

$w:=a[from];a[from]:=a[to];a[to]:=w;/*$output$*/$

end;

begin

{main

program}

for$i:=1$ to k-l do callcombination-serverto

mitialize$n[i]$-combinationsoutof

size

$[i]$ items;

for$i:=1$ to$k$ do begin

$a[i]:=i,$$up[i]:=i;p[i]:=i;c[i]:=1;d[i]:=- 1$;

end;

repeat

$i:=up[1];up[1];=1$;

call combination-server for next combination for item$i$;

if$i<k$then_move(i);

if$c[i]=C(n[i], n)$ then begin$/*$ checking alastchild $*/$

Re-initialize combinations of item$i$ for

reverse

direction;

up$[i]:=up[i+1]$;

up

$[i]:=i+1$; $c[i]:=1$; $d[i];=- d[i]$; end until$i=n$; end.

Re-initializationofcombinationsof item$i$ mustbedone in$O(1)$time. This willbementioned in

thenext section Thevalueof$C(n[i], n)$ is potentiallylarge, andmaynotbe contained in

a

single

precision variable.We

can

use

theterminationcondition in theAlgorithm4$(i=0)$ in the appendix, andbringthe effecttothecalling site. Asinitializationforcombinations of item $i$takes$O(n[i])$

time,Algorithm 3 takes$O(n)$time atthe beginning. As the size of

an

object of$n[i]$-combinations

is $O(n[i])$, thetotalspace requirementis $O(n)$

.

Inthe appendix

we

declarefixed-sized arrays for

readability. It isstraightforward to allocate

necessary space

dynamicallyusing the ”calloc” hnction inC.

Nowweexplainhow to computebase$[i]$

.

Let$l=n[i]$

occurrences

ofitem$i$be $i_{1},$

$\ldots,$

$i_{l}$

.

Letthe

as

follows: LEFT$[i]=N(i_{1})+\ldots+N(i_{l})$

.

Thenbase$[i]$

can

becomputed

as

base_$[i]=$ LEFT_$[i]/n[i]$

.

LEFT$[i]$ is initializedto_{$n[i]^{*}(n[1]+\ldots+n[i- 1])$}

.

Whenitem$i$ anditemj

are

swapped in “move” where $i=a[from]$ andj$=a[to]$,LEFT$[|]$ isupdatedby LEFT$[|]=LEFT[|]+$(from-to).

Example. (1,1,3,2,2,3,4) changes to(1,1,3,3,2,2,4). Since from$=4$andto$=6$,LEFT[3] changes from 6 to 4. This isbecause item3 goes leftovertwo ofitems 2. Note thatLEFT[2] doesnot change

as

LEFT isconcemedwithloweritems.

6.

_{Review of Takaoka’s algorithm for in-place combination generation.}

Wedescribe

an

0(1) time algorithmforgenerating the set$S$ofcombinationsofn elementsout of

theset $\{$1,

$\ldots,$$r\}$

.

Inthe following

array

$q$

” is _the

main

container

of combinations and $a$” is

an

auxiliaryarrayforbook-keeping; itkeeps trackoftreetraversalwith

some

delay. We state

a

few lemmas describing

necessary

propertiesfor

our

multi-setpermutation generation.

Example The twisted lexico tree forcombinations of4elements outof6 elements is givenwith the contents ofarray $a$” and _$q$” atthe leaves. Awhite circle is forevenparity and blackforodd.

level$0$ level 1 leve12 leve13 leve14 array

a

array $q$ 1234

1234

1235 1235

1236

1236 1246 1246 1245 1245 1256 1265 1356 1365 1345 1345 1346 1346 1456 1546 2456 2546 2346 2346 2345 2345 2356 2365 3456

4365

Lemma 1. The set$S$ generatedbythe twisted lexico-tree generatescombinations with

one

Now

we

describe implementationdetails. There

are

many

nodes which have only

one

child downto the leaf, causing straight lines. Traversalof these lines downwards will

cause

$O(n)$ time.

Having one child is caused byanode with the maximumpossible labelat thelevel. To control the

position to which

we

come

down,

we

keep an array“down”. In the above example,

we

use

“up”

to go from Ato $B$, and

use

“down”to go from$C$toD. A snapshot of the movement islike (...,

F,A,$B,C_{2}D,E,$ $\ldots)$

.

As

we see

below,

we

cannotgenerate combinations inlabels attachedto the

nodes of thetwisted lexico-tree witha fixed numberofchanges. Letarraya containthose labels.

Then

we

have

a

situation

with

$a=(a_{1}, \ldots,a_{i\cdot 1}, a_{i}, \ldots,a_{j}, \ldots,a_{n})$and $a’=(a_{1}, \ldots,a_{i- 1}, a_{i}+1, \ldots,a_{j}+1\ldots,a_{n})$,

where $a_{k+1}=a_{k}+1$ for$i\leq k<j$,

or

a

symmetric

case

where$a’=(a_{1}, \ldots,a_{i- 1}, a_{i^{-}}1, \ldots,a_{j}- 1, \ldots,a_{n})$,

where $a_{k+1}=a_{k}- 1$

.

Notethat $i$” isthedifferencepoint and $j$” is thesolutionpoint. In the fustcase,

$a_{i}$

” goes

out of the combinationand $a_{j}+1$”

comes

into the combination like

a

revolving door

system. Wekeepthe combinations in

array

$q$” and

use

array

$a$” forbook-keeping.As

we

cannot

changej$- i+1$ placesin $a$” in0(1) time,

we

just change $a_{i}$ and$a_{j}$, andchange the contents of$q$

correspondingly. Thus

we

do not implementline 11 of Algorithm2 toprepare forthe opposite

path to thenext object. Tokeep track ofthepositions of these elements in$q$,

we

usearray”pos”.

Solution points

are

maintainedinarray“solve”. Since

some

$paMs$ofarray $a$”

are

notmaintained

to the correspondinglabels in the tree,

we use

Boolean

array

mark”to show

no

maintenance. When mark$[i]=mle$,the

proper

value ofa[i-l]

is

givenby

its

child$a[i]$

.

Themainpartofthe algorithm followsin which

up

$[i]$, down$[i]$, solve$[i]$, and

pos

$[i]$

are

initializedto$i$ for all$i$

.

The

values of$d[i]$

are

initializedto 1 and those of “mark” to false. Line-by-line explanationfollows

the algorithm. If

we

change theterminationcondition atline23 to false

we

can

keepgenerating

combinations in forward orderand

reverse

order alternatelyfor

ever.

The proofof thenext lemma is omitted.

Lemma2. The generationof combinations inthe binary vector form by the above twisted

lexico-tree does not changethe relativeorder of$0’ s$

.

Items 1

move

fromtheleftendandfinishatthe

right end forone

mn

in the binary vector. From the second

mn

on, the movement altemates in direction.

To continueto generate combinations in

reverse

order,

we

can

simplyperform$i;=down[i]$,

andrepeat from line

3.

In the

source

listin the Appendix,

we

use

Algorithm4

as

“combination-server”,where all variables

are

indexed byitem. Thus simple variablesbecome one-dimensional

arraysandone-dimensional arrays become two-dimensionalarrays. Re-initialization in Algorithm

3

can

be implementedby performing $i[I]=down[I][i[I]]$foritemI. Also “checking

a

lastchild” canbeimplementedbytesting $i[I]=0$”. In the program,Algorithm3 andAlgorithm4

communicatethrough globalvariables,whichmake thealgorithm stmcmre less transparent, but efficiencyis gained. WhenAlgorithm 4 is used

as

”combination-server”, line2 and 23 willbe

removed.

Algorithm4.In-placealgorithmforcombinations {arrays $a,$$q,$ $d$,

up, pos,

sol, solve,mark

used}

1. $d[n+1]:=- 1$;up$[0]:=0;i:=n$; initialize $d[i]$to 1,andotherarrays to$i$ forall$i;d[0];=0$;

2. repeat

3.

output(q); $/*$ This isto output$q^{*}/$

4. if$mark[i]=true$then begina[i-l]:$=a[i]- 1;mark[i]:=false$ end;

5. if$d[i+1]<0$ then begin $/*$ Moving ffoman

even

nodeto

an

odd node$*/$

6. $q[pos[a[i]]]:=a[i]+d[i]$; pos$[a[i]+d[i]]:=pos[a[i]]$

7. end else begin

9. $q[pos[a[i]]]:=a[solve[i]]+d[i]$;pos$[a[solve[i]]+d[i]]:=pos[a[i]]$ 10. end else If $d[i]<0$_{then begin} $/\star$Moving from odd to even, with

$a$”value decreasing $*/$

11. q[pos[a[solve[i]]]]:$=a[i]+d[i]$;

pos

$[a[i]+d[i]];_{-)}7P[a[solve[i]]]$ 12. end;

13. $a[i]:=a[i]+d[i]$;

14. if$d[i+1]>0$ then $a$[solve$[i]$] $;=a[solve[i]]+d[i]$;

15. $up[i];=i$;

16. if$(d[i]>0)$_and $(a[i]=r- n+i)$

or

$(d[i]<0)$ _and $(a[i]=a[i- 1]+1)$then begin

17. up$[i]:=up[i- 1]$;up$[i- 1]:=i- 1$;

18.

down[up[i]]:$=i$;

19. if$d[i]<0$ then_begin solve[[up[i]]:$=i;mark[i]:=true$end;

20.

$d[i]:=- d[i]$;

21. if$(d[i]<0)$or $(i=n)$then$i:=up[i]$ else$i;=down[i]$

22. end else$i;=down[i]$

23. until$i=0$;

{This

terminationcondition is replaced by_{false for}an_{infinite loop}}

24.

output(q).

Line4: Update the parent whenmaintenance isnotdone. Lines 5-12: Update the contents of$q$

.

Lines5-7: Note that$d[;+1]$

was

alteredinaprevious_step. Thuswe_regardparity$(a_{i})$

as

even

despite$d[i+1]<0$

.

_{Move from}$B$ to $C$with$i=1$ forexample in the figure.

Lines 8-10: Siinilarly

move

from$F$ toAwith$i=2$ forexample.

Lines 10-12: Similarly

move

from$D$ to $E$with$i=2$ for example.

Line

13:

Take the next child.

Line 14: Changethe value ofaatthe solutionpoint.

Line 15: Originate thedestinationfor descendantsto

come

upto. Thisvalue will possibly propagate downin line 17.

Line 16: Check if the node is alast child.

Line 17: Compute the correct value of up”.

Line

18:

Let theancestorknowwhere to

come

downnext.

Line 19: Ifparity is odd, update thesolutionpointfor ancestorby$i$

.

Thismayfurther be updated

by larger $i$

.

Also signal that theparenta[i-l] isnotupdated for the nextobject. Ifup

$[i]arrow- 1,$$a[iarrow 1]$

has been given

a

proper

value of$a[i]- 1$_,but signaling $mark[i]=tme$”_{will not}

cause

any_harm.

Line 20: Changetheparityat$i$

.

Line 21: Goup ifyou hit

a

last child with

even

parity orat

a

leaf Otherwise go down. Line 22: Godownifyoudo nothit

a

lastchild.

Line 23: Go outofiteration if you

come

totheroot,

or

goback toline 2forrepeated generation. 7.Concluding Remarks

Weshowed how to design

a

loop-less algoritlun for multiset permutation generation basedon a

two-levelapproach. To avoid complications,weused

an

abstract algorithm, called“combination

server”, whichdelivers combinationsofvarioussizes

one

by

one

atthe request of the

upper

algorithmofJohnson-Trotter. If

we

implement

our

algorithm completelyin

a

procedural language,

we

can use

two-dimensional

arrays,

anotherdimension corresponding to which kind ofitems

are

moving. The

source

codeinAppendix is based onthisapproach by two dimensional

arrays.

Note that with thisapproach,

memory

requirement

can

be $O(n)$, where$n$isthe total sizeof each

permutation. Precisely speaking,

we

wouldneed tomaintaineight arrays ofsize$n[i]$ foreachitem

$i$

.

Thosearraysneedtobemaintainedbypointersfor dynamic memoryallocation, althoughthe

main containerofpermutationsremains tobe

a

fixedarrayofsize$n$

.

Inthe

upper

structureof the

arrays of various sizes areused and in [17] an arrayof size$n$and nine arrays ofsize$k$areused. It

remains to be

seen

whether

we can

mrther$Simpl1\mathfrak{h}^{r}$ thealgorithm

or

reduce

memory

requirement.

Itis hopedthat the multi-levelapproach

can

be extended to the $O(1)$timegeneration ofother complicatedcombinatorial objects.

References

[1] Bitner, J.R., G. Ehrlichand E.M. Reingold, “Effcient GenerationofBinaryReflectedGray

Codeandits Applications,” CACM 19 (1976)pp. 517-521.

[2] Canfield,E. R., and S. G. Williamson, A

loop-free

algorithm

for

generating the linear

extensions

of

a

poset, Order

12

(1995)

57-75

[3] Chase,P. J., Combinatorialgeneration and graylex ordering, CongressusNumerantium,69

(1989)

215-242

[4] Eades, P and McKay, B, Analgorithmforgenerating subsetsoffixedsize with

a

strong

minimal change property, Info. Proc. Lett., 19(1984) 131-133.

[5] Ehrlich, G., Loopless algorithms for generating permutations,combinations, and other combinatorialconfigurations,JACM, 20 (1973)500-513.

[6] Heap, B.R., “Pennutations by Interchanges,” Computer Joumal 6 (1963)

pp. 293-294

[7] Johnson, S.M., “GenerationofPermutationsby Transpositions,” Math. Comp.

15(1963)282-285.

[8] Joichi, J.T,,D.E. White, and S.G. Williamson,CombinatorialGraycodes, SIAM Jour. Comput., 9(1980) 130-141.

[9] Korsh, J and S. Lipschutz, GeneratingMultiset Permutations in ConstantTime,” Jour. Algorithms, 25 (1997)

pp.

321-335.

[10] Korsh, JandLaFollette,P. S., Loopless

array

generation of multiset permutations, The ComputerJoumal

47

(5)$(2004)612- 621$

[11] Lehmer, D.H., “TheMachine Tools ofCombinatorics,”in AppliedCombinatorial

Mathematics (E.F.BeckenbachEd.),Wiley, NewYork(1964)pp. 5-31.

[12] Mikawa,KandTakaoka, T, ”GenerationofParenthesis Strings by transpositions,” Proc. The Computing: The AustralasianTheory Symposium(CATS ‘97) (1997)51-58.

[13] Ruskey, F. and Savage,C., A Graycodeforcombinations of

a

multi-set, European Jour. combinatorics, 68(1996) 1-8.

[14] Savage, C., Asurveyof combinatorial Gray codes,SIAM Review,39 (1997) 605-629.

[15] Takaoka,T, $O(1)$ Time Algorithms for Combinatorial Generationby Tree Traversal,

Computer Journa142, 5 (1999)

400-408

[16] Takaoka, T., An$O(1)$Time Algorithm for GeneratingMultisetPermutations, ISAAC 1999, LNCS 1741 $(1999)237- 246$

.

[17] Takaoka, T. andViolich, S., Fusing Loopless Algorithms forCombinatorial Generation,

InternationalJoumal ofFoundations ofComputerScience, Vo118, no2 $(2007)263- 293$

.

[18] Vajnovszki,V., On the loopless generationof binary tree

sequences,

Info. Proc. Lett.,68

(1998)$113- 117$

[19] Vajnovszki,V., Alooplessalgorithmforgeneratingthepermutations ofamultiset, Theoretical Computer Science, 307 (2) $(2003)415A31$

[20] Walsh, T.R., Generationof well-formed parenthesis stringsinconstantworst-case time,Jour.

Algorithms, 29,(1998) 165-173

[21] Wilf,H.S., CombinatorialAlgorithms: An Update,SIAM,Philadelphia, 1989.

Appendix. Program Source List in $C$

Forthe readability this

program

isbased

on

two-dimensionalarrays for local variables for

combinationgeneration.Available athttp://WWW.cosc.canterbury.ac.nz/tad.takaoka/muitiperm.c

//up to 10 tems. up to multipl icity of 20

//array _{Ms the main container of multiset permutati}

_ons

nt tti

$i$nt 1,

K.

$N[10]$ , A[101, $P[10]$

.

_{$D[10]$ , UP}[10]1

int $R$, count; $i$nt countk, init, COUNT, _$f$rom, to;

int $M[40]$_, base_[401, $|$ imit[40]; $/*$ array “1 imit” is “size” in the

text $*/$

$|$

’

nt a[10][20], $q[10][20]$, up$[10][201$

.

solve$[10][20]$

.

$d[10][20]$, pos[10][20], mark[10] [201, _down[10] [20],

$i[10]$ ;

$|I$nt true$=1$

, false$=0$,

init-baseO

{int $i$

.

$k$;

base$[1]=0$; _//base$[i]$ is LEFT$[i]$ in the text

for$(k=2;k\langle=K;k++)$base[kl$=base[k-1]+N[k-1]$ _,

for$(k=1;k\langle=K;k++)|$ imit$[k]=R$-base$[k]$ ; $//|$ imit$[k]$ si

ze

of the world for $k$

for$(k=1:k\langle=K;k++)$base$[k]–base[k]*N[k]://$ base$[k]$ is multipl ied by $N[k]$

$\}$

OUTO

{int $i$ ;

for $(i=1;i\langle=R;i++)$printf$(”*d$ ”,$M[i])$ ;

printf(” base $\prime\prime$ );

for$(i=1, i\langle=K;i++)$printf$(”*d$ ”,base_$[i])$ ;

printf(”COUNT$=$%d$\backslash$n”, COUNT) ; $\}$

MOVEO

{int $w$;

from$=from+base[1]/N[I];to=to+base[1]/N[1]$ ; $//no$

.

_of $i\langle 2$

$w\vec{-}M[from]:M[from]=M[to]:M[to]--w$, //3 311222

base[$M$[from]]$=base[M[from]]+from-to$; // $*$

$COUNT++$; OUTO; _{// base[2]} $=2*3=6$

$main(\{int]k,$

$j$;

$////3321122$

base $[2]=6-2=4$

$pr$intf$(”$lnput $K$

:

number of kinds of tems ”);

scanf(”%d’’, _&K); getchar $()$ ; //no of dist$i$nct $i$tems

printf(”lnput multipl _{ici ties} of each kind of tems ”):

for$(1=1;|\langle=K;|++)$scanf($\acute\acute$

%d$\acute\acute$

,

&N

[1]);

getchar$0$

:

$R_{-}^{-}0$; for$(1=1;|\langle=K:1++)R=R+N[1];//$ Total size

$//M$ is the main contai

ner

_of permutati

ons.

$M$ is initial ized to $(1_{I}1,1,2,2,3,3\ldots)$ etc.

$tt=clock()$ ;

$init=1$ ,

for$($countk$=1$ ;$countk\langle=K;countk++)$

{

for$(1=$init$;|\langle=init+N[countk]-1;|++)$ {

$M[1]=countk$;

$\}$

init$=init+N$[countk] ;

1

for $(1=1;1\langle=R;1++)$printf_{$(”\%d ", M[1])$} ; printf$(”*n”)$ ;

init-base

$()$ ;

for $(1=1 ; 1 \langle=K-1;|++)$ {combi-init(1, $N[1]$_, $|$ mit[1]);}

$/***Johnson$_-Trotter upper _structure $***/$

for$(1=1;1$_{く$=K; I++)\{A[1]=1 ; D[|]=1 ; P[1]=1;UP[1]=1;\}$} COUNT$=1$; OUT$0$ ; do{ $1=UP[1]$ ; UP$[1]=1$ ; comb$i$ (1, $N[1]$ , I imit[1]); if$(|\langle K)$MOVE(1); $if(i[11==0)\{$ $i[1]=down[1][i[1]]$; UP[I]$=UP[1+1]$ ; UP$[1+1]=1+1$ ; $D[|]=-D[|]$ ; $\}$ $\}$wh$i$ le$(1 !=K)$ ;

pri_ntf$(”ti$

me

%d$\backslash$n”, clock$()-tt)$ ; $\}$

$/***$ lnitial izati

on

for _combi $***/$ combi$arrow init$(int $t$, int _$n$, int $r$) $\{$

{ int $i$ ;

for $(i=1;i\langle=n:i++)\{a[t][i]=i,$ $q[t][1]=i;d[tl[i]=1,$$\}$

for $(i=0;i\langle=n;i++)\{up[t][i]=i$ ; _down$[t][i]=i$ ; pos$[t][i]=i$ ; _solve$[t][i]=1$ ;$\}$

1

$d[t][n+1]=-1$ ; _{up $[t][0]=0;i[t]=n$};

$\}$

$/***$ _Combination _generati

on server

$***/$

combi (int $t$_, int $n$, int r) $\{//t$ for item

1nt 1 ; $ii=|’[t]$ , if$($mark $[t][ii]=true)$ $[$

a

$[t][ii-1]=a[t][i$ il-l; mark$[t][ii]=false$ ;$\}$ if$(d[t][ii+1]\langle 0)$ {

from$=q[t]$ $[$pos$[t]$ [a$[t][ii]]]$

:

$q[t]$ $[$pos$[t]$ [a$[t][ii]]]$

$=a[t][|i]+d[t][ii]$ ;

$to=q[t]$ [pos$[$

tl

[a$[t][ii]]]$

:

pos$[t]$ [a$[tl [ii]+d[t][ii]]=pos[t]$$[a [t][ii]]$

:

$\}$ else

if$(d[t][ii]\rangle 0)$

{

$from=q[t]$ [pos$[t]$ [a$[t][ii]11$ ;

$q$[tl $[$pos$[t]$ [a$[t][ii]]]=a[t]$ [solve$[t][iil]+d$$[$

tl

$[i$ il;

$to=q[t]$ $[$pos$[t]$ [a$[t][ii]]]$ ;

pos$[t]$ $[$

a

$[t]$ [solve$[t][ii]]+d[t][ii]]=$

pos$[t]$ [a$[$

tl

$[ii]]$

$\}$ else if$(ii\rangle 0)\{$

$q[t]$ [pos$[t][a\underline{\lceil}t]$ [solve$[t][i$ ]]]$]=a[t][i|]+d[t][ii]$ ;

$to=q[t]$ [pos$[t]$ [a$[t]$ [solve$[t][ii]]]$_];

pos[$tl$ $[a [t][ii]+d[t][ii]]=pos[t]$ [a$[t]$ _{[solve [tl $[ii]]$ ];}

$\}$

a

$[t][ii]=a$[tl _{$[ii]+d[t][ii]$} ;

if$(d[t][ii+1]\rangle 0)$

a

$[t]$ [solve$[t][|’|’]$]$=a[t]$ [solve$[t][ii]$]$+d[t][ii]$ ;

up $[t][ii]=ii$ ;

if$(((d[t][ii]\rangle 0) \ \ (a [t][ii]==r-n+ii))||$

$((d[t][ii] \langle 0) \ \ (a [t][ii]==a[tl[iiarrow 1]+1)))$

{

up$[t][ii]=$

up$[t][ii-1]$ ; up[tl[ii-l]$=ii-1$ ,

down$[t]$ $[up [t][ii]]=ii$ ,

if$(d[t][i ] \langle 0)$ {solve$[t]$ $[up [t][ii]]=$ii ;

mark$[t][ii]=true:\}$

$d[t][ii]=-d[t][ii]$

:

if$((d[t][ii]\langle 0)||(ii-=n))$

$i[t]=up[t][ii]$ ; elsei $[t]=down[t][ii]$,

$\}$ else $|r[t]=down[tl[ii]$ , $\}$