OS1206 <M&M2012 カンファレンス・2012 年
9月
22〜24日>
Copyright©社団法人
日本機械学会
1.
緒 言
近年,小型化,軽量化を目的とし,異なる材料を 接合した異材接合体が,幅広い分野で用いられてい る.このような,異材接合体では,材料の物性値の 違いにより,接合界面角部で応力が無限大となる特 異応力場が発生することが問題視されている.特異 応力場は接合界面での剥離を生じさせ,材料の強度 を低下させる原因の一つと考えられているため,定 量的な評価が必要と考えられている.また,特異応 力場は材料の組み合わせや接合界面の寸法,形状に より変化するため,特異応力場の定量的な評価を行 うには接合界面の寸法が特異応力場に与える影響を 明らかにする必要がある.
そこで,本報告では,メッシュフリー法
(1)(2)を用 いて半導体パッケージの断面を想定し,内部に
Si介在物(シリコン介在物)を有する樹脂製の試験片 モデルを対象とし,接合界面における特異応力場の 強さを求める.また,本報告では
Si介在物角部の曲 率半径を変え,介在物角部の曲率半径が特異応力場 の強さに与える影響について検討を行う.
2.
エレメントフリーガラーキン法による応力解析 図1 に示すように3 次元空間に節点のみが存在する場 合を考える.任意の節点を評価点として,その評価点を 中心に半径
R(影響半径)の球を描き,球の内部の領域を Ωk,境界をΓ
k,評価点から参照点までの距離d
I,
I番目の 参照点におけるx 方向の変位をu
Iとする.ここで,
Iは参 照点の番号である.任意の評価点での
x方向の変位の近 似関数u
hを式(1)に示す.
uh(x,y,z)=
{ }
g T{ }
a (1){ }
g T ={
1 x y z}
,{ }
a T ={
a0 a1 a2 a3}
(2)
ここで,
{g}は基底ベクトル,{a}は未定係数ベクトルを表す.ここで,各評価点においてu
hとu
Iの差を最も小 さくする様な未定係数ベクトル
{a}を決定するために,式(3)に示す評価関数J を定義する.
J=
#
I=1n{
!I({ }
gI T{ }
a "uI)2}
(3)三次元エレメントフリーガラーキン法による自由表面の 交点近傍における特異応力場の解析
(角部の曲率半径が特異応力場に与える影響)
塚田靖幸
*1,古口日出男
*1,倉橋貴彦
*2Analysis of stress singularity field near the cross point of inclusion and free surface by 3D element free Galerkin method
(Influence of radius of curvature at vertex for stress singularity field)
Yasuyuki TSUKADA
*1,Hideo KOGUCHI
*1and Takahiko KURAHASHI
*2*1 Nagaoka University of Technology, Kamitomioka 1603-1, Nagaoka, Niigata, Japan
*2 Nagaoka National College of Technology, Nishikatagai 888, Nagaoka, Niigata, Japan In this research, we investigate intensity of stress singularity near cross point of inclusion and free surface by 3D element free Galerkin method (3D EFGM). Especially, we focus on a case that corner of silicon has small radius of curvature. In this study, stress analysis was carried out by changing value of the radius, and relationship between intensity of stress singularity and the radius is investigated. From the results, it was found that stress value near the corner decreases, and exponent of the approximation function decreases with increasing the radius at corner.
Key Words : Composite Material , Intensity of Stress Singularity , Interface , 3D EFGM
!
I = 1"6 dI R
#$% &
'(
2
+8 dI R
#$% &
'(
3
"3 dI R
#$% &
'(
4
, 0)dI)R
0, dI>R
* +, -,
(4)
ここで,
ωIは領域
Ωk内における重み関数であり,n は領域
Ωk内に存在する参照点の数である.また, 重み関 数
ωIは式(4)に示す 4 次のスプライン関数を用いる.こ こで,未定係数ベクトル
{a}についてのJの停留条件によ
り,
{a}が決定される.{a}を式(5)に示す.
{ }
a =[ ]
A!1[ ]
B{ }
u(5)
ここで,行列
[A],[B]は式(6)に示す行列である.[ ]A = (!I{ }gI { }gI T) I=1
"
n , [ ]B =$%!1{ }g1 # # # !n{ }gn &'(6)
式(5)を式(1)に代入することで式(7)に示す補間関数 が得られる.
uh(x,y,z)=
{ }
gT{ }
a ={ }
g T[ ]
A!1[ ]
B{ }
u ={ }
"{ }
u
(7)
ここで,
{Φ}は形状関数である.同様の方法により,y方向の変位,
z方向の変位に対する形状関数を求める.求 められた形状関数を用いて剛性方程式を誘導する.本手 法では,形状関数に移動最小二乗法を使用しているため,
直接的に境界条件の値を与えることができない.そのた め,境界条件を満足させるためにペナルティ法を適用す る.剛性方程式を解き変位分布を求め,得られた変位分 布より応力分布を求める.
Fig.1 Domain Influence
3.
固有値解析による特異性オーダの計算
特異応力場を特徴づける特異性オーダλは,
Pageau らにより提案された有限要素法による固有 値解析
(3)により求められる.固有値解析では固有値
pが求まり,固有値
pと特異性オーダの間には,
λ=1-p
となる関係がある.この固有値
pは式(8)の固 有方程式を解くことにより求めることができる.
(
p2[ ]
C +p D[ ]
+[ ]
E) { }
q =0 (8)ここに,
[C],[D]及び[E]は有限要素法により導かれた係数行列であり,{q}は変位ベクトルである.式(8) の導出は参考文献
(3)を参照して頂く.
4.
数値解析例
4・1
解析モデル
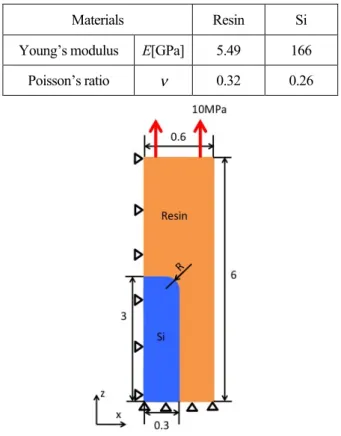
本報告では実際の半導体パッケージをもとにした,内 部にSi 介在物を有するResin 片を解析モデルとする.モ デルの寸法,形状は図
2に示すものとする.
y方向の厚 みは0.1 mm である.図2 の曲率半径R が3.125μ
m,6.25μ
m,12.5μmのモデルを作成しエレメントフリーガラー
キン法を用いて応力解析を行う. モデルの節点数は11412,
セル数は
8080となっている.外力はモデル上面に
W=10MPaの引張応力を与える.対称性を考慮した1/4 モ デルとして解析を行うため,図
2に示すように,モデル 左側面を
x方向に,モデル下面を
z方向,紙面裏側の面 をy 方向にそれぞれ固定する.ペナルティ数は,
1 1030とした.最小節点間隔は
3.125μ
mとなっている.影響 半径は評価点ごとに自動計算し,評価点が属するバック グラウンドセルを包括できるような大きさとなっている.
モデル表面に図3 のようにR=0 の場合の
Si角部を原点o とした極座標系(
r,θ)をとり,界面曲率部近傍での応力σ
θθの分布を求める. 解析に用いた物性値を表1 に示す.
Table 1 Material properties
Materials Resin Si
Young’s modulus E[GPa] 5.49 166
Poisson’s ratio ν 0.32 0.26
Fig.2 Computational Model
Fig.3 Coordinate of near the radius interface
4・2
解析結果および考察
図4 に各曲率半径における図
3原点
oからの距離
rに
対する
φ=90 degの応力σ
θθの分布を示す.ここで図4 は
両対数グラフで表したものである.図
4より界面に近づ くにつれて応力
σθθが増加し特異応力場が発生している ことがわかる. また,曲率半径R が大きくなるに従い全 体的に応力σ
θθが減少していることがわかる.
図4 の応力分布を式
(9)の特異応力場の式で近似し,特異応力場の強さを求める.
!!! !,! =!!!! !+! !! (9)
ここで,
K1θθは
r方向の特異応力場の強さ,rは図3 の座
標系原点からの距離,
dは図 3 の原点
oから界面までの 距離である.距離r と式
(9)の指数部λの関係を図
5に,
原点からの距離r と特異応力場の強さK
1θθ,の関係を図
6にそれぞれ示す.図4 の各応力分布に対して式(9)を用い て特異応力場の強さ
K1θθおよび指数部
λを求めた.本報 告のモデルではR が
0の場合以外では,角部曲率部を拡 大すると直線的な界面形状になっている.そのため式
(9)を用いて近似を行うと指数部
λの値はR=0 のモデルで
λvertex,
それ以外のモデルで
λlineとなる.しかし,図5 よ
りR が大きくなるに従って
λの値が小さくなっているこ とがわかる.これは,各モデルでR が変化していること
により式
(9)のdも変化したためであると考えられる.図
6
より,Si 介在物角部の曲率半径
Rが大きくなると特異 応力場の強さが小さくなっていることがわかる.
5.
結論
EFGM
を用いて角部に微小な曲率を持つ異材接合体 の応力解析を行った.内部にSi 介在物を持つ
Resin片の シリコン角部の曲率半径を変え,曲率半径が特異応力場 に与える影響について調べた.その結果,曲率半径が大 きくなるに伴い,特異応力場が弱くなり,また特異応力 場の近似関数の指数部の値も小さくなることがわかった.
参考文献
(1)Belytschko, T., Lu. Y. Y. and Gu, L., Element-Free Galerkin Method, Int. J.
Number. Methods Eng., 37(1994), 229-256.
(2)Tomoyuki Saito, Noboru Tomioka and Akifumi Okabe, Three Dimensional Stress Analysis of Dissimilar Materials With Crack Using Element Free Galerkin Method, JSME 20th Computational Mechanics Conference, (2007),759-760
(3)Pageau, S. S. and Bigger, Jr. S. B., Finite Element Evaluation of Free-Edge Singular Stress Fields in Anisotropic Material, Int. J. Number. Methods Eng., 38(1995), 2225-2239.
Fig.4 Distribution of stress σθθ against distance r from Si-Resin interface
Fig.5 Exponent of the approximation functionλagainst radius R
Fig.6 Intensity of stress singularity K1θθ against radius R
3x105 4 5 6
stress σθθ , Pa
30 25 20
15 r , μm
R=0 R=3.125 R=6.25 R=12.5 'Curve fitting'
0.5
0.4
0.3
0.2
Exponent of the approximation function λ
12 10 8 6 4 2
0 radius R , μm
1.6x106
1.4
1.2
1.0
0.8
0.6
Intensity of singularity K1θθ , Pa
12 10 8 6 4 2
0 radius R , μm