つくばリポジトリ PRB 97 7 75430
全文
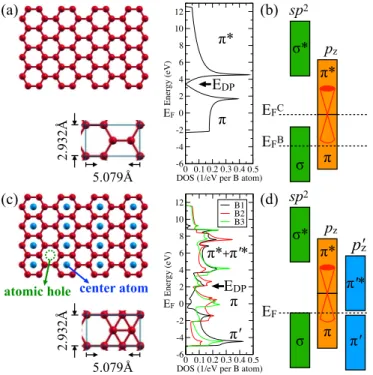
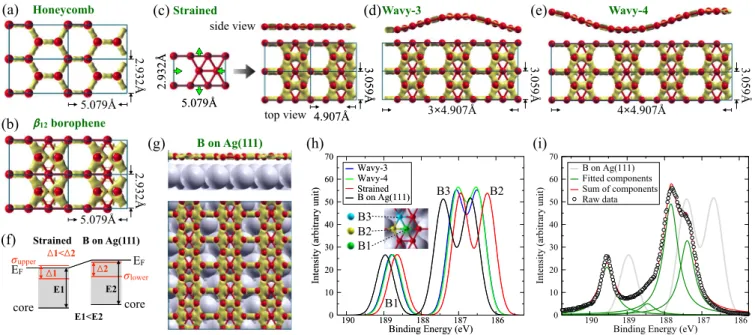
図
関連したドキュメント
We show that a discrete fixed point theorem of Eilenberg is equivalent to the restriction of the contraction principle to the class of non-Archimedean bounded metric spaces.. We
Using an “energy approach” introduced by Bronsard and Kohn [11] to study slow motion for Allen-Cahn equation and improved by Grant [25] in the study of Cahn-Morral systems, we
(4) The basin of attraction for each exponential attractor is the entire phase space, and in demonstrating this result we see that the semigroup of solution operators also admits
It should be mentioned that it was recently proved by Gruji´c&Kalisch [5] a result on local well-posedness of the generalized KdV equation (KdV is an abbreviation for
“Breuil-M´ezard conjecture and modularity lifting for potentially semistable deformations after
Then it follows immediately from a suitable version of “Hensel’s Lemma” [cf., e.g., the argument of [4], Lemma 2.1] that S may be obtained, as the notation suggests, as the m A
We construct a sequence of a Newton-linearized problems and we show that the sequence of weak solutions converges towards the solution of the nonlinear one in a quadratic way.. In
In this section we state our main theorems concerning the existence of a unique local solution to (SDP) and the continuous dependence on the initial data... τ is the initial time of