Fourier Niching Approach for Multi-modal Optimization 2 Yan Pei Hideyuki Takagi 2 Graduate School of Design, Kyushu University 2 2 Faculty of Design,

(1)

九州大学学術情報リポジトリ

Kyushu University Institutional Repository

多峰性最適化のためのフーリエ・ニッチ法

裴, 岩

九州大学大学院芸術工学府

高木, 英行

九州大学大学院芸術工学研究院

Pei, Yan

Graduate School of Design, Kyushu University

Takagi, Hideyuki

Faculty of Design, Kyushu University

http://hdl.handle.net/2324/1434428

出版情報：第2回進化計算学会研究会第8回進化計算フロンティア研究会合同研究会, pp.189-195,

2012-03. 進化計算学会

バージョン：accepted

権利関係：

(2)

多峰性最適化のためのフーリエ・ニッチ法

Fourier Niching Approach for Multi-modal Optimization

裴岩

1∗

_高木英行

2

Yan Pei

1

_{Hideyuki Takagi}

2

1

_{九州大学大学院芸術工学府}

1

_{Graduate School of Design, Kyushu University}

2

_{九州大学大学院芸術工学研究院}

2

_{Faculty of Design, Kyushu University}

Abstract: We propose a niching method for solving multi-modal optimization problems from their frequency information and evaluate its performance with six multi-modal benchmark func-tions. We use Fourier transform as the main analysis tool to obtain the frequency information and estimate the potential modal locations of the ﬁtness landscape using the obtained frequency and phase information. We choose the estimated potential modal locations as elite points, directly put them into the population, and ﬁnd more peaks within local search areas restricted by given search radiuses. Experimental evaluation results show that our proposed Fourier niching method has the better performance, especially from the computational cost point of view.

1 はじめに

進化計算応用の中には，大局的最適解を得るだけでなく，多様な良い解を得ることが有用であり必要である最適化問題がある．そのような応用例の１つがアートや工業デザインである．この種の応用には，デザインコンセプトに合った多様な良いデザインを得ることが重要である．また，デザイナにヒントやインスピレーションを与える解の探索を主とする応用もあろう．進化計算には大局的最適解を速く簡単に探し出す能力があるが，多峰性最適化問題の局所最適解を探し出す能力は欠けている．そのため色々なニッチ保存手法が提案されている．ニッチ手法の先駆けは次式の適応度シェアリング法である [1]． Fshared(i) = Foriginal(i) ∑N j=iSH(dij) SH(dij) = { 1− ( dij σshare) α _{if d} ij > σshare 0 otherwise (1)

ここで，Fshared(i)，Foriginal(i)，SH(dij) は，各々シェ

アリングされた適応度，本来の適応度，シェアリング 関数である．2 個体間の距離 dij が σshare以下の時に適応度のシェアリングが行われる． ∗_{連絡先：九州大学大学院芸術工学府} 815-8540 福岡市南区塩原 4 丁目 9 番 1 号 Email: peiyan@ieee.org 個体群をニッチに分けるクラスタリング手法が提案されている [2]．ここでの適応度は個体とニッチの中心との距離によって求められる．種の間で繰り広げられる限られた自然の資源の獲得競争にヒントを得た混雑度の概念は文献 [5] に見られる．この混雑度を制約とする 2 つの混雑度計算手法（確定的混雑度 [3] と確率的混雑度 [4]）が提案された．その他にも，多峰性最適化問題のための制約トーナメント選択法 [6]，特徴付けられた個体による限られた資源のシェアリング過程をシミュレーションする clearing 法 [7]，多峰性最適化問題のための種保存 GA [8] などが提案されている．これまでに提案されたすべてのニッチ法は適応度の調整や制約された演算にのみ焦点を当ててきたが，探索過程での適応度景観は考慮してこなかった．しかし，多峰の数情報や局所探索領域情報があれば，これらの情報を使うことでニッチ法の性能向上が図れる可能性がある．本論文では，探索空間の周波数特性を利用するフーリエ・ニッチ法を提案する．探索空間の周波数特性は，多峰の局所ピーク領域とピーク数情報を知る 1 つの方法であり，他にも利用情報はあろう．離散的フーリエ変換で得られた適応度景観の周波数，位相，振幅特性から，本来の探索空間のでの多峰領域と個数情報を得る．この情報を利用することで，新しいニッチ法「フーリエ・ニッチ法」が構築できる．以下，本論文は，第 2 節で提案するフーリエ・ニッチ法

(3)

の基本について述べる．第 3 節では差分進化（DE/best/1/bin）と 6 つのベンチマーク関数を使って，提案手法の性能評価を行い，第 4 節で提案手法について詳しく考察し，今後の検討項目と展開の可能性を示す．最後に今後の研究方向を示して全体をまとめる．なお，本論文では，大局的最適解や複数の局所最適解を略してピークと記することにする．

2 フーリエ・ニッチ法の提案

2.1 適応度景観の周波数特性

離散的フーリエ変換（DFT）で周波数特性を得るには，探索空間を等間隔にリサンプルする必要がある．いくつかのサンプリング方法が考えられ実験的に比較評価した [9] が，本論文ではその中から，”global 1 dimen-sion” サンプリング法 [9] と高速フーリエ変換（FFT）を用いる．FFT は X(k) = N 2−1 ∑ n=0 [x(n) + (−1)kx(n +N 2 )]W nk N で表される．ここで，Wkn N = e− 2kπN , (0≤ k ≤ N − 1) で，x(n), X(k), n, N は，各々，本来の信号サンプル 系列，DFT 変換後のサンプル系列，本来の信号のサンプル変数，信号サンプル数である．表 1 中の 2 種類の多峰性ベンチマーク関数 F1 と F2 を図 1 に示す．F1 は同じ振幅の局所最適解が等間隔に並び，F2 は異なる振幅の局所最適解が異なる間隔で並んでいる例である．これら適応度景観のサンプル点をフーリエ変換することで，図 2 に示す振幅周波数特性が得られる． 0 0.2 0.4 0.6 0.8 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Test Function 1 x Function Value 0 0.2 0.4 0.6 0.8 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Test Function 2 x Function Value (a) (b) 図 1: 表 1 中の F1 と F2 の適応度景観

2.2 局所最適解の存在範囲と個数の計算

適応度景観の各次元毎にリサンプル点をフーリエ変 換し，周波数（Fi），位相（bi），振幅（Ai）を得た後，振幅の大きな主周波数成分のみをフィルタリングし，これを探索空間のピーク位置と個数の計算に利用する [9]． 0 20 40 60 80 100 120 140 0 20 40 60 80 100 120 140 160

Frequency content of Test Function 1

Frequency (Hz) Amplitude 0 20 40 60 80 100 120 140 0 20 40 60 80 100 120

Frequency content of Test Function 2

Frequency (Hz) Amplitude (a) (b) 図 2: F1 と F2 のパワースペクトラム逆フーリエ変換によって，元探索空間の 1-D 適応度景観は f (x) = a0+ n ∑ i=1 (aicos(ωix) + cisin(ωix) + bi) で表される．提案手法では近似モデルとしてパワー振 幅のみを用いるので，apcos(ωpx) + cpsin(ωpx)，即ち，

√ a2 p+ c2pcos(ωpx + bp) と bp = tan−1(ap/cp) で表現 できる．cos(x) 関数では最小値は Ti = 1/Fiとすると (Ti/2) + biに位置するので，各次元でのピークは ki ( 1 2∗ Fi ) + bi 周辺に存在する．ここで Rangeiを探索空間の i 番目の 次元の探索幅（上限−下限）とすると，kiは， ki= ⌊ Rangei Fi ⌋ の床関数で求められる i 番目の次元のピーク数である． 全空間のピーク数 N は，1 次元に写像した時のピーク の重なりも考えると， max(k1, k2, ..., kn)≤ N ≤ n ∏ i=1 ki の範囲の値になる．

2.3 エリートの挿入と探索半径の導入

ピーク領域とピーク数の情報から，探索のエリート候補になる座標がピークもしくはピーク周辺に得られる．これらの探索エリート点を個体群の最悪個体と入れ替えることで個体群に加える．加えられたこれらのエリートがそのまま最終のピーク点になるわけではない．なぜならば，通常の進化計算では親個体はより適応度の高い子個体に置き換えられ，置換点はどこにでも生じ得るからである．この点を考慮して，エリート個体が次世代で子個体に置き換えられる範囲を制限すべきであり，ここにエリート探索半径の概念を導入する．

(4)

探索半径はエリート個体が置き換わられる範囲をピーク点の周辺領域に限るため小さな値とする．本論文では，探索半径を式（2）に示す．探索半径 = Rangei m∗ ki (2) ここで m は調整パラメータで，本論文では m = 2 と する．

3 評価実験

3.1 多峰性ベンチマーク関数

提案するフーリエ・ニッチ法を評価するために，6 つの多峰性ベンチマーク関数を用いる．F1 は適応度の等しいピークが等間隔に配置する 1 次元関数，F2 はピークの適応度と分布が等しくない 1 次元関数，F3∼F6 は 2 次元関数で，各々，Shekel の Foxholes 関数， Rastrigin 関数，Schwefe 関数， Griewank 関数である．これらの形状と数式を図 1 と図 3，および，表 1 に示す．表 1 の探索範囲には，F1 と F2 は 5 つのピーク， F3∼F6 は各々，25, 121, 49, 59 のピークがある． F3 F4 F5 F6

図 3: Shekel の Foxholes 関数，Rastrigin 関数，Schwefe 関数，Griewank 関数の 2 次元形状．

3.2 実験方法

前述の多峰性ベンチマーク関数を評価するために，差分進化（DE/best/1/bin）に提案のフーリエ・ニッチ法を組み合わせて適用する． F1 と F2 では，パラメータ範囲が 0≤ x ≤ 1 で個体数が 100，表 1 の F3∼F6 では，パラメータ範囲が表 1 で，個体数 1,000 で行う．この条件で 50 試行行う．フーリエ・ニッチ法では，得られたピーク数に応じて式（2）で探索半径を決める．提案フーリエ・ニッチ法と性能比較をするために，シェアリング法とハイブリッド法（シェアリング法＋提案フーリエ・ニッチ法）も評価する．シェアリング法のパラメータ設定は式（1） の σshare= 0.3 とする． フーリエ変換の点数は， F1, F2, F4 が 256 点サンプリング，F3 と F6 が 64 点サンプリング，F5 が 8 点サンプリングである． 2 つのベンチマーク関数では最適値の数が判ってい るので，ピーク数 (NP eak) と計算時間を評価指標として用いる．各関数で 50 試行し，表 2 と図 4 を得た．表 2: DE と組み合わせる手法毎の，F1 と F2 の最適化 1 回にかかった計算時間（単位は ms）

Func. Method Time NP eak

F1 none 14.09 1 F1 Sharing 99.99 2 F1 Fourier 17.83 5 F1 Sharing+Fourier 107.46 5 F2 none 8.11 1 F2 Sharing 100.33 2 F2 Fourier 16.24 5 F2 Sharing+Fourier 106.12 5

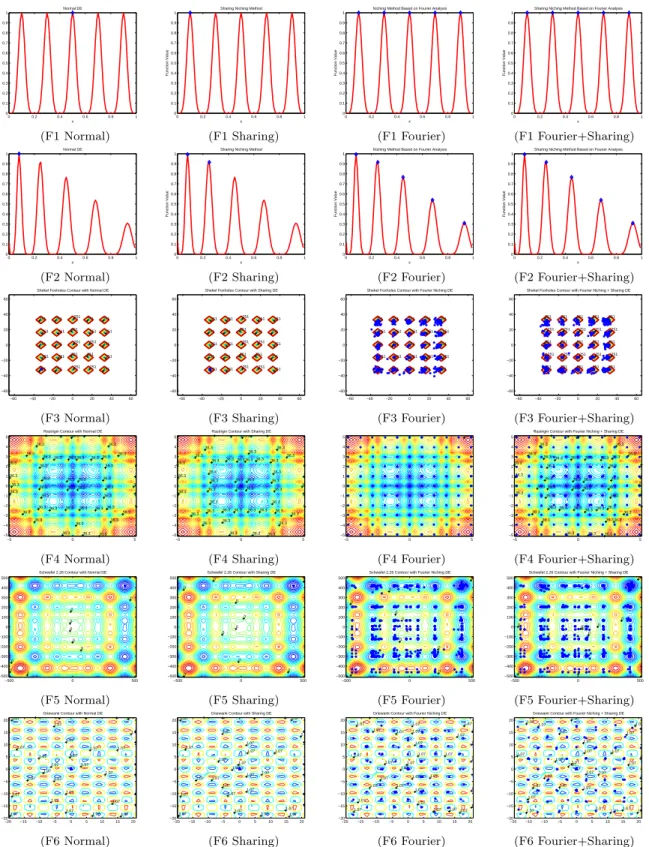
3.3 実験結果

表 2 と図 4 より，以下のことが判る． 1. 提案フーリエ・ニッチ法は F1 と F2 関数の全ピークを得ることができた． 2. 提案フーリエ・ニッチ法は通常の DE やシェアリング法に比べ，より多くの F3∼F6 関数のピークを得ることができた． 3. シェアリング法の 1 回では F1 と F2 関数の 2 種類のピークしか得られず，F3∼F6 関数では 1 つのピークしか得ることができなかった．提案方法はシェアリング法に比べて，ピーク分類の点でも優れていると言える． 4. F3∼F6 関数では，提案フーリエ・ニッチ法は（フーリエ・ニッチ法＋シェアリング法）のハイブリッド法とほとんど同じピーク分類を得ることができた．

(5)

表 1: 評価実験で用いるベンチマーク関数．Range, n, C はパラメータレンジ，関数の次元数，関数の性質を示し， M, U, N, S は，各々，多峰性，単峰性，分離不可，分離可，を示す．

No. Name Test function Range n C

F1 Niching1 f (x) = sin6(5πx) [0,1] 1 MN F2 Niching2 f (x) = e−2(ln2)(x−0.010.8 )2_sin6_(5π(x0.75− 0.05)) _[0,1] ₁ _MN F3 Shekel’s Foxholes f (x) = [0.02 +∑25_j=1_j+∑2 1 i=1(xi−aij)6] −1 _[_{−65.536, 65.536]} ₂ _MS F4 Rastrigin f (x) = (10n) +∑n_i=1(x2 i− 10 cos(2πxi)) [-5.12,5.12] 2 MS

F5 Schwefel 2.26 f (x) =∑n_i=1(−xisin(

√ |xi|)) [-512,512] 2 MS F6 Griewank f (x) = 1 +∑n_i=1 x2i 4000− ∏n i=1cos( xi √ i) [-20,20] 2 MN 5. 提案フーリエ・ニッチ法の計算コストはシェアリング法，および，ハイブリッド法よりも少ない．

4 考察

提案手法の性能

表 2 から，多峰性最適化問題のために提案したフーリエ・ニッチ法を 6 つの多峰性ベンチマーク関数で評価した結果，すべての関数でシェアリング法よりも多くのピークを少ない計算時間で得ることができた．提案手法は F1 と F2 関数の全ピークを少ない計算時間で得ることができた．F3∼F6 関数では，提案手法はほとんどのピークを検出したものの全ピークではなかった．これは，大雑把な位置情報を得るためのフーリエ変換に探索空間の 1 次元データを用いてエリート点数を限ったためである．大規模多峰性問題を扱う場合，より良い最終結果を得るには，提案フーリエ・ニッチ法適用時の個体数をピーク数以上にセットしなければならない．

フーリエ変換

フーリエ変換の主目的は探索空間の適応度景観を得て，大局的・局所的最適解の大体の位置を探すことである．正しい周波数情報を得ることは提案手法の成功の鍵であり，このための色々なデータサンプリング法も提案した [9]．実際の多峰性最適化問題でよりよい性能を示すためには，問題に適した周波数情報を正しく得るための適切なサンプリング法と FFT 点数の設定が肝要である．

周波数分解能

周波数分解能は正しい周波数値を得るための重要な概念で，これによって DFT 点数が決定される．周波数分解能は， ∆f = fs N, で与えられる．ここで，∆f は 2 つの隣接周波数最初差 を意味する周波数分解能，fsは帯域周波数，N は DFT 点数である．FFT では N は 2 のべき乗でなければな らない． 8, 16, 32, 64, 128, 256 点の異なるサンプル点数で F5 関数をフーリエ変換して，本提案手法を評価した．図 5 の実験結果が示すように，サンプル点数が増えるほど探索空間の正確な周波数情報が得られるわけではなく，周波数分解能，すわなち，周波数帯域とサンプル点数のバランスに依存する，と言える．図 5 では，サンプリング数が増えるにしたがってフーリエ・ニッチ法で得られるピーク数が少なくなっている．これは，周波数分解能が低下し，低周波数を区別できないためである． 0 0 0 0 0 0 0 0 0 0

Schwefel 2.26 Contour with Fourier Niching DE by 8 sampling

−500 0 500 −500 −400 −300 −200 −100 0 100 200 300 400 500 0 0 0 0 0 0 0 0 0 0

−500 0 500 −500 −400 −300 −200 −100 0 100 200 300 400 500

(F5 with 8 sampling) (F5 with 16 sampling)

0 0 0 0 0 0 0 0 0 0

−500 0 500 −500 −400 −300 −200 −100 0 100 200 300 400 500 0 0 0 0 0 0 0 0 0 0

−500 0 500 −500 −400 −300 −200 −100 0 100 200 300 400 500

0 0 0 0 0 0 0 0 0 0

−500 0 500 −500 −400 −300 −200 −100 0 100 200 300 400 500 0 0 0 0 0 0 0 0 0 0

−500 0 500 −500 −400 −300 −200 −100 0 100 200 300 400 500

図 5: フーリエ変換のサンプル点数変えて提案手法を F5 関数に適用した結果．

(6)

0 0.2 0.4 0.6 0.8 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Normal DE x Function Value 0 0.2 0.4 0.6 0.8 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

1 Sharing Niching Method

x Function Value 0 0.2 0.4 0.6 0.8 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

1 Niching Method Based on Fourier Analysis

x Function Value 0 0.2 0.4 0.6 0.8 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

1 Sharing Niching Method Based on Fourier Analysis

x

Function Value

(F1 Normal) (F1 Sharing) (F1 Fourier) (F1 Fourier+Sharing)

0 0.2 0.4 0.6 0.8 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Normal DE x Function Value 0 0.2 0.4 0.6 0.8 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

1 Sharing Niching Method

x Function Value 0 0.2 0.4 0.6 0.8 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

1 Niching Method Based on Fourier Analysis

x Function Value 0 0.2 0.4 0.6 0.8 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

1 Sharing Niching Method Based on Fourier Analysis

x

Function Value

251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 Shekel Foxholes Contour with Normal DE

−60 −40 −20 0 20 40 60 −60 −40 −20 0 20 40 60 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 Shekel Foxholes Contour with Sharing DE

−60 −40 −20 0 20 40 60 −60 −40 −20 0 20 40 60 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 Shekel Foxholes Contour with Fourier Niching DE

−60 −40 −20 0 20 40 60 −60 −40 −20 0 20 40 60 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 251 Shekel Foxholes Contour with Fourier Niching + Sharing DE

−60 −40 −20 0 20 40 60 −60 −40 −20 0 20 40 60

36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 Rastrigin Contour with Normal DE

−5 0 5 −5 −4 −3 −2 −1 0 1 2 3 4 5 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 Rastrigin Contour with Sharing DE

−5 0 5 −5 −4 −3 −2 −1 0 1 2 3 4 5 36.3 −5 0 5 −5 −4 −3 −2 −1 0 1 2 3 4 5 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 36.3 Rastrigin Contour with Fourier Niching + Sharing DE

−5 0 5 −5 −4 −3 −2 −1 0 1 2 3 4 5

0 0 0 0 0 0 0 0 0 0 Schwefel 2.26 Contour with Normal DE

−500 0 500 −500 −400 −300 −200 −100 0 100 200 300 400 500 0 0 0 0 0 0 0 0 0 0 Schwefel 2.26 Contour with Sharing DE

−500 0 500 −500 −400 −300 −200 −100 0 100 200 300 400 500 0 0 0 0 0 0 0 0 0 0 Schwefel 2.26 Contour with Fourier Niching DE

−500 0 500 −500 −400 −300 −200 −100 0 100 200 300 400 500 0 0 0 0 0 0 0 0 0 0 Schwefel 2.26 Contour with Fourier Niching + Sharing DE

−500 0 500 −500 −400 −300 −200 −100 0 100 200 300 400 500

1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 Griewank Contour with Normal DE

−20 −15 −10 −5 0 5 10 15 20 −20 −15 −10 −5 0 5 10 15 20 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 Griewank Contour with Sharing DE

−20 −15 −10 −5 0 5 10 15 20 −20 −15 −10 −5 0 5 10 15 20 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 Griewank Contour with Fourier Niching DE

−20 −15 −10 −5 0 5 10 15 20 −20 −15 −10 −5 0 5 10 15 20 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 1.07 Griewank Contour with Fourier Niching + Sharing DE

−20 −15 −10 −5 0 5 10 15 20 −20 −15 −10 −5 0 5 10 15 20

(7)

探索半径

フーリエ・ニッチ法では，局所ピーク領域を探索するエリートを残すために，最終ピークを探索するエリートが探索する範囲を制限する探索半径の考えを提案した．これは，大局的あるは局所的最適解を探索するエリートには重要なパラメータで，提案手法の性能を改善するためにこの値をいかに調整するかは今後の重要な研究テーマである．

計算コスト

提案フーリエ・ニッチ法はシェアリング法と比較して計算コストが少ない．これは，提案手法が個体の初期化後 1 回適用するだけなのに対し，シェアリング法は全世代あるいは一定世代毎に各個体の適応度を調整し直す必要があるからである．この点が提案手法の長所である．当然のことながら，提案フーリエ・ニッチ法はシェアリング法＋フーリエ法よりも計算コストが少ない．得られた最終ピークの category では，フーリエ・ニッチ法でえられたものの方がシェアリング法＋フーリエ法よりも多い．図 4 から，フーリエ・ニッチ法はシェアリング法＋フーリエ法よりも収束特性がよい．

5 結論と今後の課題

本論文では，多峰性最適化問題のためにフーリエ・ニッチ法を提案した．本手法の手順には，周波数情報の獲得，ピーク存在位置の推定，エリートの配置と探索範囲の限定，の 3 段階がある．評価結果から，提案手法は実現が容易で実用的であり，特に計算コストの点で優れている．周波数分解能の設定はこの手法の成功の鍵である．分解能が低い場合は適応度景観の細かい変化（高い周波数成分）が区別できず，分解能が高い過ぎる場合は，低周波数成分を区別できない．したがって，適応度景観が未知の場合には，正しい周波数を得るために異なる周波数分解能で提案手法を適用してみる必要がある．広い周波数帯域を得るには適切な周波数分解能を適用することが肝要である．この点は今後の課題である．探索半径も提案手法の成功のための重要なパラメータである．探索半径が大きすぎる場合，エリートがピーク位置を外れてしまうかもしれないし，小さすぎる場合は収束が遅くなるかもしれない．エリート毎の適応探索半径値調整法が最適な解決法であり，その実現は今後の課題としたい．

謝辞

本研究は科学研究費（課題番号 23500279）の助成を受けたものである．筆者の裴岩は吉田奨学会からの奨学金を受けて本研究を遂行した．ここに感謝する．

参考文献

[1] D. Goldberg and J. Richardson, “Genetic al-gorithms with sharing for multi-modal function optimization”, 2nd Int. Conf. on Genetic Algo-rithms (ICGA1987), pages 44–49, Cambridge, MA, USA, July, 1987.

[2] X. Yin and N. Germay, “Investigations on solving load ﬂow problems by genetic algorithms”, Elec-tric Power System Research, vol.22, no.3, pages 151–163, Elsevier, 1991.

[3] Samir W. Mahfoud, “Crowding and preselection revisited”, Parallel Problem Solving from Nature (PPSN1992), vol. 2, pages 27–37, Brussels, Bel-gium, Sept., 1992.

[4] O. Mengsheol and D. Goldberg, “Probabilis-tic crowding: Deterministic crowding with probabilistic replacement”, 1999 Genetic and Evolutionary Computation Conference (GECCO1999), pages 409–416, Orlando, FL, USA, July, 1999.

[5] Kenneth A. De. Jong, “An analysis of the be-havior of a class of genetic adaptive systems”, Technical report, University Microﬁlms No. 76-9381, Doctoral dissertation, University of Michi-gan, 1975.

[6] Georges Harick, “Finding multi-modal solutions using restricted tournament selection”, 6th Int. Conf. on Genetic Algorithms (ICGA1995), pages 24–31, Pittsburgh, PA, USA, July, 1997.

[7] A. P´etrowski, “A clearing procedure as a niching method for genetic algorithms”, 3rd IEEE Int. Conf. on Evolutionary Computation (ICEC1996), pages 798–803. Nagoya, Japan, May, 1996.

[8] J. P. Li, Marton. E. Balazs., T. P. Geoﬀrey, and P. John Clarkson, “A species conserving genetic algorithm for multi-modal function op-timization”, Evolutionary Computation, vol.10, no.3, pages 207–234, MIT Press, 2002.

(8)

[9] 裴岩，高木英行「適応度景観のフーリエ解析による進化的探索高速化の試み」進化計算シンポジウム 2011，岩沼，pp.167–173 (2011 年 12 月）.