Analysis of Time-Dependent In-Plane Deformation of Laminated Composites Based on a Homogenization Theory(Composite 2)

NII-Electronic Library Service

Analysis

of

Time-Dependent

In-Plane

Deformation

ofLaminated

Composites

Based

on

a

Homogenization

Theory

'Iletsuya

_MATSUDA',

_Nobutada

_OHNO'"

and

Hiroki

TANAKA"

*

Department

ofMicro

System

Engineering,

Nagoya

University,

Furo-cho,

Chikusa-ku,

Nagoya

464-8603,

Japan

"*

Department

ofMechanical

Engineering,

Nagoya

Uniyersity,

Furo-cho,Chikusa-ku,Nagoya464-8603,Japan

In

this

work,

the

homogenized

elastic-yiscoplastic

behavior

of

long

fiber-reinforced

laminates

under

in-plane

loading

is

_preclicted

by

taking

directly

into

account

the

micro-scopic

structure

and

stacking

sequence

of

laminae.

[[b

this

end,

a

hernogenization

theory

of nonlinear

time-dependent

composites

is

applied

to

such

laminates,

leading

to

the

macro-scopic

rate-type

constitutive

equation

of

laminates

and

the

evolution equations ofmicro-scopic and average

stresses

in

each

lamina.

The

macroscopic

constitutive

equation

has

a

stifT}iess

tensor

and a stress relaxation

function

which

are

evaluated

explicitly

in

terms

of

the

microscopic structure and stacking sequence

of

laminae.

Tb

verify

the

_present

theory,

uniaxial

tensile

tests

are

_performed

on carbon

fiberfepoxy

Iaminates.

It

is

_thus

shown

that

the

_present

theory

is

successfu1

in

_predicting

the

anisotropic

yiscoplasticity

in

in-plane

ten-sion

of

unidirectional

and

cross-ply

laminates

and

the

negligible

viscoplasticity exhibited

by

_{quasi-isetropic}

laminates.

Key

}Pbrtts

:

Laminate,

Fiber-reinforced

composite,

In-plane

deformation,

Viscoplasticity,

Homogenization,Anisotropy

1.

Introduction

Fiber-reinforced

laminated

composites

are

now

im-portant

engineering materials.

CFRP

(carbon

fiber-rein-fOrced

_plastics)

laminates

be}ong

to

this

type

of

compos-ites.

Such

composites

consist of

laminae,

each of which

is

unidirectionally

reinforced

with

long

fibers.

Macroscopic

responses

of

laminated

composites

are

usually

predicted

by

attaining

the

overall responses of monolayers and

then

by

averaging

thern

in

accordance with

the

stacking

se-quence

of

laminae,

and

appropriate

methods such as

the

Mori-Tanaka

theory(i}

and

the

cells

model

of

Aboudi{2)

can

be

employed

for

attaining

the

overall

responses

of

monolayersC])'C6}.

These

models

are

fairly

successfu1

but

are

based

on

approximated

fields

of microscepic

stress

and

strain,

resulting

in

_possible

errors

especially

when

inelastic

deformation

occurs

in

constituents.

It

is,

there-fore,

worthy

developing

a

theory

by

which

the

inelastic

behavior

of

fiber-reinforced

}aminates

can

be

simulated

accurately.

The

present

authors constructed a

homogenization

theory

for

nonlinear

time-dependent

composites with

periodic

microstructures(7)'

(g).

This

theory

is

based

on unit

cell

_problems,

in

which

the

so-called

rperiodicity

of

perturbed

displacement

is

utilized as

its

boundary

condi-tion(9Hi2).

The

theory

deyeloped

by

the

_present

authors

enables

us

to

analyze

not

only

the

macroscopic

elas-tic-viscoplastic

behavior

of

composites

but

also

the

mi-croscopic

time-dependent

distributions

of

stress

and

strain

in

unit

cells.

The

_present

authors

further

showed

the

fo11owing(i3):

tfthe

microscopic

distributions

of

stress

and strain are symmetric with respect

to

the

center

of

each unit ceLl,

the

field

ofperturbed velocity satisfies

the

point

symmetry

with

respect

to

the

cell

boundary

facet

centers; as a consequence,

semiunit

cells

can

be

taken

as

the

domain

of analysis, so

that

computation

time

can

be

reduced

significantly.

Then,

the

homogenization

theory

was rebuilt using semiunit cel]s and was employed

for

computing

elastic-viscoplastic

behavior

of

fiber-rein-forced

unidirectional composites.

The

homogenization

theory

mentioned above

is

ex-pected

to

accurately

_predict

the

macroscopic

elas-tic-viscopiastic

behavior

of

fiber-reinforced

laminates,

since

the

theory

can

have

the

merit of

directly

bringing

the

microscopic

structure

of

laminae

into

_predicting

the

macroscopic

response

of

laminates.

The

theory

can

have

another

merit

of

enabling

us

to

analyze

the

microscopic

distributions

of stress and strain

in

each

lamina.

These

-The Japan Society of Mechanical Engineers

TheJapanSociety of Mechanical Engineers

merits cannot

be

available

ifother

theories

are

employed.

It

is,

therefore,

of significance

to

apply

the

homogeniza-tion

theory

_to

simulating

the

time-dependent

nonlinear

behavioroffiber-reinforcedlaminates.

In

this

work,

the

homogenization

theory

developed

by

the

_present

authors

is

used

for

deriving

a

macroscopic

constitutive

equation

applicable

to

the

_in-plane

elas-tic-viscoplastic

behavior

of

long

fiber-reinfbrced

Iami-nates.

The

macroscopic

equation

is

ofthe

rate-type

and

is

characterized

by

a

stiffhess

tensor

and

a

stress

re]axation

function

which are evaluated

in

terms

ofthe microscopic

structure

and

stacking sequence

ofIaminae.

To

verify

_the

present

theory,

_uniaxial

tensile

tests

are

_performed

on

carbon

fiberlepoxy

laminates.

It

is

thus

shown

that

the

present

theory

is

successfu1

in

_predicting

the

anisotropic yiscoplasticity

in

in-plane

tension

of

unidirectional and cross-ply

laminates

_and

the

neg]igible

yiscoplasticity

ex-hibited

by

_{quasi-isotropic}

laminates.

2.

Theory

2.1

Basicassumptions

Let

us

consider

a

Iaminate

in

which

long

fiber-rein-forced

laminae

are

stacked

symmetrically

(Fig.

_1).

_Let

us

assume

that

the

fibers

are

arranged

unidirectionally and

periodically

in

each

lamina,

and

that

the

fibers

deform

elastically

_while

the

matrix

exhibit

elasticity

and

vis-coplasticity.Let

N

and

f(")

bethenumberof]aminae

and

_the

voiume

fra6tion

ofthe

ath

lamina,

respectively.

It

is

then

convenient

to

employ

_three

kinds

of

Cartesian

coordinates,

i.e,,

_X,

(i=1,2,3)

fbr

_the

_]aminate,

_x,(a'

(i

=

1,

2,

3)

for

the

_a

th

lamina,

_and

yla'

(i

--

1,

2,

3)

for

the

unit cell

in

the

ath

lamina,

Y(a),

as

shown

in

Fig.

1,

The

X,

axis

is

taken

in

the

stacking

direction.

The

xlf)-axis

is

parallel

to

the

X,-axis

and

thus

di-rected

_{perpendicularly}

to

the

Iateral

surface

of

the

ath

lamina.

The

x;a}-axis

is

_taken

in

the

fiber

direction

of

the

ath

lamina

and makes

an

angle

e(a)

with

the

X,

axis,

The

_yla)-axis

is

_parallel

to

_the

xfa)-axis

but

is

employed

solely

for

the

unit

cell

Y{cr)

.

Let

us

assume

further

that

the

laminate,

which

is

in-finitely

large

in

the

X,-and

X,

-directions,

_is

subject

to

in-plane

Loading,

_giying

rise

to

no

bending

because

ofthe

symmetry

in

stacking.

Then,

the

macroscopic

stress

in

the

laminate,

X.,and

the

overall

stresses

in

laminae,

.T,(,a),

satisfy

,v

X,

-Zf(")

,..El:cr),

(1)

a.1

2I12 =4,=E,, =O,

e)

.xl,a)=.,xlf'=.xl.cr,)=o, cr=1,2,...,N,

(3)

where _.()

stands

for

the

components with respect

to

the

X,

coordinate

system.

Moreover,

themacroscopic

strain

in

the

laminate,

E,i,

and

the

oyerali

strains

in

laminae,

E,(,a)

, are

a]lowed

to

satisfy

E:]

=xE-(f)

Ca)

.

.E

2I

-It

is

obvious

that

Eq

the

xia)

coordinatesystem

.x{,") =.Egf}

(a}

rE2i

-.

E,,

=.

Eff)

,

E,,

=.

EJ(]a)

,

a-I,

2,...,N,

(4)

.4,E,,=Zf(a).E;:),

(5)

a=1

E2i=En

==O,

(6)

.Elf' =O, _a=1,

2,

...,N.

(7)

s.

(3)

and

(7)

also

hold

with respect

_to

-.2]g,a)=o, _a-1,2,...,N,

(s)

.El:'=O, a=1,

2,

...,

?V

.

(9)

X3

li1,

x

te

(a)

Laminate

Fig.

1

!

l

!llXJ

(b)

Lamina

Structure

ofa

laminate

and

three

kinds

o

(c)

Unit

Cell

NII-Electronic Library Service

2.2

Homogenizationinlaminae

Let

us

denote

the

microscopic

distributions

of stress and strain

in

the

unit cell

Y(")

of

the

ath

lamina

as

a;:"'(y,t)

and

_aScr'(y,t),

where

_y

and

t

denote

_y,

and

time,

respecti"ely.

Then,

_the

overall

stress

and

strain

in

the

ath

lamina,

_.X,i") and _.E:a}, are evaluated

by

homogenizing

crL")(y,t)

and

E,ia)(y,t)

using

a

vol-ume average operhtor

<#>=yl.)

L,.,#dy`"',

ao)

where

Y(a)

indicates

the

volume of

Y(").

We

assume

that

each

constituent

in

the

ath

tamina

has

a constitutive

relation

d},a)=cL:,)[S:,a}-13:f)],

(11)

where

(')

denotesthedifferentiation

with respectto

t,

and cL? and

fl:ia)

indicate

an elastic stiffhess

tensor

and

Viscoplastic

function

satisfying cL? =c:7 =c!,:) =cEZ) _and

lltf}=

13)1").

It

is

noted

that

_{cE:? and}

lilff)

change

from

constituent

to

constituent;

for

the

fibers,

fiEf)

yanishes.

Then,

we

can

show

the

fo11owing

relations, which

satisfy a]1

fundamental

equations

such

as

the

equilibrium equation

of

stress,

the

relation

between

displacement

and strain,

the

constitutiye

relation,

etc.(71

{8)i

6,1"'(y,t)=at7(y,t).,EL",(t)-i;1")(y,t),

(12)

.X',1")=<ava).E2ff'-(r,Ca'),

(l3)

where

aLZ' - cL:;

(6,,

fi,,

+z:[;a'),

(i4)

r,la)=.L7(17{,a}+opf,)).

(15)

Here,

_a,

denotesKronecker'sdelta,

₍

_),,

indicatesthe

differentiation

with respect

to

y,,

and

_z,1'<a)

and

ofa}

are

the

functions

to

be

determined

by

solving

boundary

value

_prob]ems

L,.,cf,::zfl(,"'v;,T'dy`a'=-L,-cL:,'vfff,'dy`a',

(16)

Jl.,.,

cL:JopLVvEf'd/`a' -

-L,.,

_{qtz'af)vf.f)d}･{")}

,

(i7)

where vfa} signifies any

Y-periodic

velocity

field

de-fined

in

Y("]

at

t.

2.3

In-plane

e]astic-viscoplastic

constitutive

equa-tion

of

laminates

Let

us

solve

Eq.(13)

fbr

_.E'l,cr) and

transform

the

resulting

equation

in

a

matrix

form

(

,E(a))6.1 =

[B(cr}]6.6

(

,iS(a))b.1

+(cCa>}fi.1

.

(ls)

Then,

Eqs.(8)

and

(9)

allow

the

above equation

to

be

reduced

_to

(,E("))3.1

=[B-(a)]1.G

[,.S(a)]3.i

_+(C-(a)]].1

,

(lg)

.Es:)

=

Bgf}..sfff'

+

Bgf)

..s;,a}

+

Blg)

..sgf)

+

c;g)

,(2o)

where

(

)

standsforthein-planeparts,i,e.,

(.x-'(cr)]=(.Si(,a)

..Sf,a) ..sli))T,

(21)

(.E-'

`a']=(,Efa,}

.Elf)

2.Ela,

}}r,

(22)

and so on.

Here

(

)T

denotes

the

transpose.

Now,

let

us

introduce

further

the

in-plane

yectors of x4") and r

E,(Ja)

, Le.

(.S'

(a)]=(..slff)

.qf) ..sl:))T,

(23)

(xE=

`"')

_==(yE,Cff'

.Elf'

2.E:l}]T.

(24)

Then,

since

the

xf"}-

and

x;a)

-axes

make

respectively

an

angle

e(a)

with

the

X,-and

X,

-axes

_(Fig.

1),

we

have

(.x-'

Ca)] ₌

[p(cr)][.x=

{a)],

_(2s)

(,E-'

(a)]

=

[e(")](.E=

(cr)],

(26)

where

[PCa)]

and

[9(")]

denoterotationmatrices.

Hence,

Eqs.(25)

and

(26)

are

substituted

into

Eq.(19)

to

_glve

(x.Ls'

Ca)] _=[p(a}]'I

[B'(a}]-

[eca}1(xEM'

{a))

-

[p(a)]'i

[B-(a)]'i

{c-(a)).

(27)

Finally,

the

above equation with

Eq.

(4)

is

substituted

into

Eq.(1)

to

_provide

a macroscopic

in-plane

constitutive

equatlon

(X=]-[Ant][EL']-(Rfi],

(28)

where

-it,,

[

A']

=

2

f(a)

[p(a)

]'i

[

B-(a}

]'i

[aa)

]

,

(2g)

a=1

N

[R-}

==

Zf{a)

[p(al'i

[BL{a)Ii

{c'ca)]

.

(3o)

a=I

Itisnotedthat

[A-]

and

{R-]

inthemacroscopicconstitutive

re1ation

(28)

depend

on

f(a),

e(a)

and

[B-(a)],which

are

evaluated

in

terrns

of

the

stacking

sequence

and

microscopic

structureoflaminae.

3.

Experimenta]Procedure

To

verify

_the

_theory

described

in

_the

_preceding

sec-tion,

uniaxial

tensile

tests

at

constant

strain

rates

were

perforrned

at room

_temperature

using

coupon

specimens

cut out

fi'om

TR30t#340

carbon

fiberlepoxy

_plates

of

300x300

mm,

manufactured

by

Mitsubishi

Rayon

Co.

Ltd,

The

_plates

were

laminates

of

three

kinds,

i.e.,

unidi-rectional,

cross-ply

and

_{quasi-isotropic}

laminates

with

the

lay-ups

of

[O],,,

[O/90],,

and

[O/

±

60],,,

which

had

-

₆₁₉

The Japan Society of Mechanical Engineers

TheJapanSociety ofMechanical Engineers

Table

ain

_gauge

Fig.2

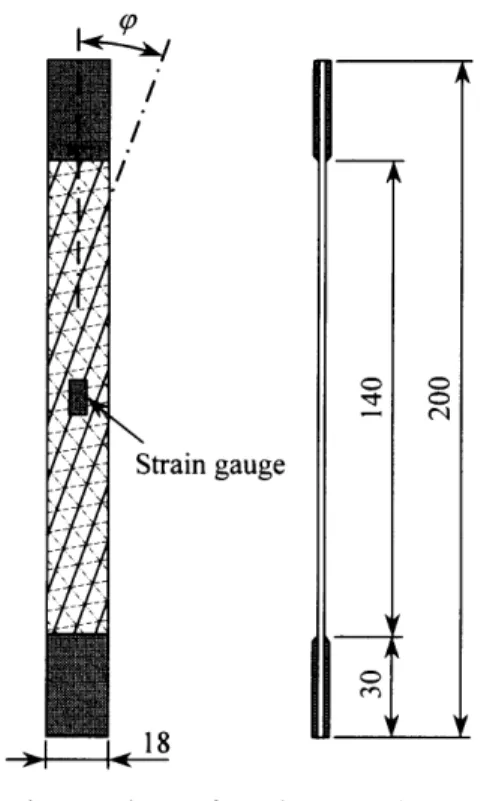
Shapeofspecimens(unit:mm)

1

Off-axis

angles

for

unidirectional,cross-ply

and

quasi-isotropic

}am

in

ates

9ooN

2

Laminate

_q

_(degree)

Unidirectional

Cross-pLy

Quasi-isotropic

O,

10,

20,

30,

45,

60,

90

O,

10,

20,

30,

45

O,

10,

20,

30

1.5,

2.0

and

2.25

mm

in

_thickness,

respectively.

The

volume

fraction

of

fibers,

Vf

_,was

56

_percent

in

each

_ply.

The

coupon specimens with rectangular

GFRP

_tabs,

which

had

the

shape shown

in

Fig.

2,

were

_prepared.

In

the

figure,

_q

indicates

the

angle

between

the

longitudi-na]

direction

of

specimens

and

the

fiber

direction

of

OO

-plies.

Henceforth

_op

will

be

referred

to

as

the

off-axis

angle.

The

values of

_q

tested

in

the

_present

work

are

listed

in

Table

1.

A

closed-loop servohydraulic

testing

machine

with

a

Ioadlstrain

computer controller

was

empleyed

for

the

tests.

The

longitudina]

strain

of

each

specimen

was

detected

by

two

strain

_gauges

adhered

on

both

its

sides and was controlled

to

increase

at a

con-stant

rate.

4.

MaterialAssumptions

4.1

Fiberarrangement

The

arrangement

of

carbon

fibers,

which

was

unidi-rectional

in

the

xla)

direction,

was medeled

_to

be

hex-agonally

_periodic

on

the

xl"}

-x:a)

_plane

in

each

lamina,

as

illustrated

in

Fig.

1.

This

is

an

idealization

ofthe

ran-dom

distribution

of

fibers

on

that

_plane

in

the

specimens

but

can

bejustified

as

follows:

The

hexagonal

_periodicity

of carbon

fiber

arTangement

_gives

rise

to

the

transverse

quasi-isotropy

not only

in

elasticity

but

also

in

elastovis-coplasticity(7}'

(8).

Such

isotropy

matches with

the

trans-verse

isotropy

brought

about

by

the

randorn

distribution

of

fibers

on

the

xf"}-xS"}

_plane.

The

hexagonal

perio-dicity

therefore

does

work

as

far

as

the

overall

response

ofeach

lamina

is

concerned.

According

to

the

above assumption,

the

unit

cell

Y{a)

was chosen

to

be

hexagonal

fbr

all

laminae,

as

shown

in

Fig.

3;

P';

was

taken

to

be

56

_percent.

Here

it

is

noted

that

Y(a}

was

_taken

_to

be

2D

rather

than

3D

since each

lamina

was

assumed

to

have

no microscopic variation

in

the

fiber

direction(S)'(i4}.

Since

the

hexagonal

unit

cell

has

the

_point

symmetry with respect

to

the

cell

center,

it

is

suMcient

to

consider

half

of

the

unit

cell

as

the

domain

ofanalysis

for

solving

Eq.(16)

and

(17)('3).

Hence,

the

upper

half

of

the

unit cel] was considered and

was

divided

into

finite

elements using

four-noded

isoparametric

elements,

as

depicted

in

Fig,

3,

4.2

Microscopic

constitutiveequations

The

carbon

fibers

were

regarded

as

a

transversely

isotropic

elastic

material.

Consequently,

the

fibers

were

assumed

to

have

five

independent

elastic

constants,

i.e,,

two

Ybung's

moduli

Ef,

and

E.t,,

two

Poisson's

ratios

vf,2 and v,f,,,

and

on'e

shear

rigidity

Gf]i,

where

the

subscripts

1,

2

and

3

signify

the

_yfa),

_y;a)

and

_y:")

directions,

respectively.

Table

2

shows

the

five

constants of

fibers

employed

in

the

_present

work;

Ef,

was

pro-vided

by

_the

manufacturer,

Mitsubishi

Rayon

Co.

Ltd,,

and

the

others were

determined

by

referring

to

Kriz

and

Fig.

3Unit

cell

and

finite

element mesh

Table

2Material

_parameters

Carbon

fiberEn

=1.55xlO`

Ef3

=:

2.40x

lo5

=2.47 ×

1o4

G

_f]I

vf,, =

O.49

vf,,

=

O.28

Epoxy

E.

=3.5xl03

v:. =O.35

S,"

=10'5 _n=35

g(gP)=141.s(E-p)Ot6S+1o

NII-Electronic Library Service

150

1OOI･E,gi

50

O

O.Ol

O.02

E]3

Fig.

4

Identification

ofviscoplastic

_properties

ofepoxy

matrlx

StinchcombCiS}.

The

epoxy

matrix,

on

the

other

hand,

was regarded

as

an

elastic-viscoplastic

materia] characterized as

EL,

-

1

'E,r,m

o･,,

-

Zn.'

a.a,

+iE,p

[g(a.i,)]

"

iit

,(3

1)

where

E.,

v. and n are material

constants,

_g(iP)

is

a

materiat

function

depending

on equivalent

_plastic

strain

iP,

S,P

is

a

reference

strain rate, s,

indicates

the

deyiatoric

_part

of

cr,i,

and

a, =[(3f2)s,s,]"i.

The

material constants

and

material

function

in

the

above

equation

were

deterrnined

by

simulating

the

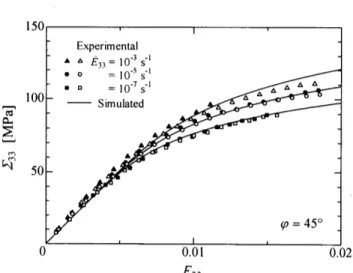
450

offLaxis

_tensile

_tests

of

the

unidirectional

laminate

at

E,,

==10'S,

10'5

and

10'7

s':

(Fig,

4).

This

_was

be-cause

the

effect of matrix

viscoplasticity

was expected

to

be

significant

in

such effLaxis

tests.

The

constants

and

function

ofthe

matrix

were

thus

obtained

and

are

listed

in

Table

2.

It

is

noted

_that

_Eq.(31),

which

is

based

on

the

assumption of

isotropic

hardening,

can

be

yalid

if

we

consider

monotonic

loading.

5.

ComparisonofExperimentsandPredictions

Uniaxial

tensile

experiments

were

done

at

Eii=

10'S

s'i

at

room

temperature

using

the

coupon

specimens

of

unidirectional,

cross-ply

and

_{quasi-isotropic}

laminates.

The

experiments

were

_predicted

by

means

of

the

_present

theory.

The

experiments

and

the

_predictions

are

compared

with each other

in

this

section.

Figure

5

deals

with

the

unidirectional

laminate

[O],,

.

As

seen

from

the

figure,

significant

dependence

on

the

offLaxis

angle

_op

was

observed

in

the

experiments:

When

_q=OO,

the

tensile

behavior

was almost

linear.

However,

a

]ittle

deviation

of

_q

from

Oe

caused

no-ticeable

nonlinearity

with

drastic

decrease

ofviscoplastic

flow

stress,

whereas

increase

of

_q

beyond

450

_gave

negligible

influence.

_This

significant

dependence

on

_rp

is

_predicted

very well using

the

_present

theory,

as shown

in

the

figure.

We,

therefore,

can

say

that

the

_present

the-ory

is

successfu1

in

describing

the

anisotropy

in

long

fi-ber-reinforced

unidirectional

composites.

Let

us emphasize

that

for

the

seven

tests

with

differ-ent

values of

_q

done

for

the

unidirectional

laminate,

the

predictions

have

excellent

agreement with

the

experi-ments,

as

discussed

in

the

aboye.

The

unidirectional

laminate

is

in

effbct

a

larnina,

so

that

only

its

microstruc-ture

is

important.

Hence,

the

excetlent agreement

between

predictions

and

experiments

means

the

following:

The

hexagonal

unit cell

introduced

for

idealizing

the

micro-structure

in

each

lamina

does

accurately work as

far

as

the

overall

response

of

a

lamina

is

concerned.

Then,

for

any

iaminate

consisting

of

such

laminae,

we can expect

that

the

_present

theory

is

successfu1

in

_predicting

its

in-plane

deformation

behaviot

Figures

6

and

7

show

the

_predictions

and

experi-ments

done

for

the

cross-ply

and

_{quasi-isotropic}

lami-nates,

_[O190],,

and

[O/

±

60],,,

respectively,

It

is

seen

that

the

_predictions

agree well with

the

experiments,

as

expected

in

the

above.

Then,

it

is

allowed

to

say

_that

_the

homogenized

in-plane

defomiation

behavior

of

long

fi-ber-reinforced

laminates

can

be

accurately simulated

by

stacking

the

Iaminae

with

_their

microstructures

repre-sented

by

the

hexagonal

unit cells.

Let

us

compare

the

stress versus strain relations

of

the

three

kinds

of

laminates.

The

cross-ply

laminate

ex-hibited

nearly

the

same

anisotropy as

the

unidirectional one under

in-plane

uniaxial

loading

with

_ep

ranging

from

OO

to

450

_(Figs,5and

6).

This

suggeststhat

the

OO-

and

90e-plies

in

the

cross-ply

laminate

interact

weakly witri each

other.

The

_{quasi-isotropic}

laminate,

on

the

other

hand,

had

isotropic

and

almost

linear

behavior

r.Eu(li

4

3

2

o

Fig.

5

O.Ol

E33

Relationsofmacro-stress

_4,

E,,

at constant strain rate

unidirectional

laminate

O.02

and

macro-strain

E,,

=10'5

s'i

for

-

₆₂₁

The Japan Society of Mechanical Engineers

TheJapanSociety of Mechanical Engineers

r.E,gz

500

400

300

200

100

O

O,Ol

E33

Fig.

6

ReLations

ofmacro-stress

4,

4,

at constant strain rate

cross-ply

laminate

O,02

and

macro-strain

E33

=10'S

s'l

for

until

fraeture

occurred around

4,=600MPa,

which

was

six

times

larger

than

the

viscoplastic

flow

stress

of

the

unidirectional

and

cross-ply

laminates

of

_q=45e.

The

almost

linear

behavior,

i.e.,

negligible

viscoplasticity,

is

a consequence of

the

lay-up

in

_[O/

±

60],,,in

which

the

Oe-

and

±

600-plies

strong]y

interact

with

one

an-other

so

as

to

induce

the

_{quasi-isotropy}

in

in-plane

de-formation.

Let

us

repeat

that

the

_present

theory

does

pre-dict

the

characteristics mentioned

above,

i.e.,

the

anisot-ropic

viscoplasticity

of unidirectional and

cross-ply

laminates

and

the

negligible

yiscoplasticity of

quasi-iso-tropic

Iaminates.

6.

Conclusions

In

this

work,

the

homogenization

theory

ofnonlinear

time-dependent

composites

developed

by

the

_present

au-thors

was utilized

fbr

_predicting

the

in-plane

elas-tic-yiscoplastic

behavior

of

tong

fiber-reinfbrced

lami-nates.

We

thus

derived

a macroscopic rate-type

constitu-tive

equation

of

laminates

as well as evolution equations of microscopic and

average

stresses

in

each

lamina,

The

macroscopic constitutive

equation

was

shown

to

have

a

stiffhess

tensor

and a stress relaxation

function

_to

be

evaluated

in

terms

of

the

microscopic

structure

and

stacking

sequence

of

laminae.

To

verify

the

_present

the-ory,

in-plane

tensile

tests

were

_performed

using

coupon

specimens

ofcarbon

fiber!epoxy

laminates

at room

tem-perature.

The

arrangement of carbon

fibers

in

each

lamina

was modeled

using

a

hexagonai

unit cell.

The

_present

theory

then

_predicted

very

accurately

the

macroscopic

characteristics

observed such

as

the

anisotropic

vis-coplasticity

of

unidirectional and cross-ply

laminates

and

the

negligible

viscoplasticity ofquasi-isotropic

laminates.

artE,gi

see

600

400

200

Fig.

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9}

(10)

(11)

(12)

C13)

(14)

{15)

O

O.Ol

E33

7

Relations

ofmacro-stress

X

and ]]

E]i

at

constant

strain rate

Eii=

quasi-isotropic

laminate

O.02

macro-straln

10-5sL'

for

References

Mori,

T.

and

Tanaka,

K,.

Acta

Met.,

ivbl.

21

(1973),

_p.

57I-574,

Aboudi,

J.,

Mechanics

ofComposite

Materials,

Elsevier

Science

Publishers,

_{1991

_).

Pindera,

M.

J.

and

Lin,

M.

W,,

ASME

J.

Press,

VesseL

1lechnoL

Vbl.

I11

(1989).

p.

183-190.

Tszeng,

T.

C.,

J.

Compos.

Mater.,

Vbl,

28

_{1994),

_p.

soo-s2e.Kawai,

M.,

Masuko,

Y.,

Kawase,

irl_and

_Negishi,

_R.,

_Int,

J,

Mech.

Sci.

_(to

appcar).

Kawahara,

K.

and

Tohgo,

K.,

Preprint

of

JSME,

(in

Japanese),

No.

O03-1

_(2000),

_p.

I45-146,

Wu,

×

.

and

Ohno,

N.,

Int,

J,

Solids

Struct.,

Vbl,

36

(1999),

p,

4991-5012.

Ohno,

N,,

Wu,

X.

and

Matsuda,

_T.,

_Int.

_J.

_Mech.

_Sci.,

Vbl.

42

_(2000),

_p.

1519-1536.

Bensoussan.

A..

Lions,

J,-L.

and

Papanicolaou,

G,

As-ymptotic

Analysis

for

Periodic

_Structures,

_North

-HollandPublishingCompany,(1978).

Sanchez-Palencia

E,.

Nen-Homogeneous

Media

and

Vibration

_1'heery,

_Lecture

_Notes

_in

_Physics

_127,

Springer-Verlag,(1980).

Bakhvalov,

N.

and

Panasenko,

G,

Homogenisatien:

Av-eraging

Processes

in

Periodic

Media

K}uwer

Academic

Publishers,(1984).

Guedes,

J.

M,

and

Kikuchi,

N.,

Comput,

Method

Appt.

Mech.

Eng.,

Vbl.

83

_(1990),

_p.

143-]98,

Ohno,

N,,

Matsuda,

T,

and

Wu,

X.,

Int,

J,

Solids

Struct.,

Vbl.

38

_(2001),

_p.

2867-2878.

Noguchi.

H.

and

Shimizu.

E.,

Trans,

Jpn,

Sec,

Mech.

Eng.,

_(in

Japanese).

Vbl.

_65,

_No,

_630.

_A

_0999),

_p.

225-231Kriz.

R.

D,

and

Stinchcomb,

W.

W.,

Exper,

Mech.,

ivbl,