TOP URL 1

あもんノート

ユークリッド幾何学、ニュートン力学から、相対論、量子論、素粒子 論、宇宙論、そして超ひも理論まで、理論物理学を簡潔にかつ幅広く網 羅したノートです。TOP へは下の URL をクリックして行けます。専用 の画像掲示板で、ご意見、ご質問等も受け付けております。 http://amonphys.web.fc2.com/

目 次

第20章 くりこみ理論 3 20.1 パラメータ公式 . . . . 3 20.2 運動量積分公式 . . . . 4 20.3 スカラー4乗模型とくりこみ因子 . . . . 5 20.4 頂点関数とくりこみ条件 . . . . 6 20.5 頂点関数のループ数展開 . . . . 8 20.6 散乱振幅の2次補正 . . . 12 20.7 QEDのくりこみ . . . 13 20.8 QEDの頂点関数の有限性 . . . 14 20.9 ファリーの定理 . . . 16 20.10 シュレーディンガー場のくりこみ . . . 17

第

20

章 くりこみ理論

相対論的場の量子論の章において、摂動の高次において生じるループグラフが 発散することを見ました。この章ではこれら発散の処理、すなわち、くりこみ理 論について簡単に解説します。スカラー4乗模型、QED, シュレーディンガー場の 量子論についてそれぞれ具体的に見ていくことにします。

20.1

パラメータ公式

くりこみの話の前に少し数学をやっておく必要があります。 まずは、 1 ab = Z ₁ 0 dx 1 (ax + b(1−x))2_, 1 abc = Z ₁ 0 dx Z _1−x 0 dy 2 (ax + by + c(1−x−y))3 といった積分公式で、ファインマンのパラメータ公式と呼ばれます。一般化した 式は、 1 a1a2· · · an = Z ₁ 0 dx1· · · Z ₁ 0 dxn Γ(n) δ (1−x1−· · ·−xn) (a1x1+· · ·+anxn)n です。ここで Γ(n) はガンマ関数です。証明は以下の通り。 [証明] 1 a1· · · an = Z _∞ 0 dt1· · · Z _∞ 0 dtne−(a1t1+···antn) = Z _∞ 0 dt Z _∞ 0 dt1· · · Z _∞ 0 dtnδ(t−t1−· · ·−tn) e−(a1t1+···antn). ここで ti = txi で積分変数を置換し、 = Z _∞ 0 dt Z _∞ 0 dx1· · · Z _∞ 0 dxntnδ ¡ t(1−x1−· · ·−xn) ¢ e−(a1x1+···anxn)t = Z _∞ 0 dx1· · · Z _∞ 0 dxnδ(1−x1−· · ·−xn) Z _∞ 0 dt tn−1e−(a1x1+···anxn)t = Z ₁ 0 dx1· · · Z ₁ 0 dxn Γ(n) δ (1−x1−· · ·−xn) (a1x1+· · ·+anxn)n. [証明終]

20.2

運動量積分公式

次に一般的な時空次元(= 2η)における運動量積分公式です。基本となる公式は、 Z d2η_k (2π)2η 1 (a2_−k2_−i²)c = iΓ(c−η) (4π)η_Γ(c)a2(c−η) です。ここで、a2 > 0, c ∈ Z+(正の整数), k2 = k·k = (k0)2−|k|2, ² → +0. [証明] k0 = ik_E0, k = kE で積分変数を置換(ユークリッド化)すると、 (左辺) = i Z d2η_k E (2π)2η 1 (a2_+k2 E−i²)c. ここで k2_E = (k_E0)2+ |kE|2 です。このとき kE0 の積分範囲は +i∞ ∼ −i∞ ですが、 a2 + k_E2 − i² = (k_E0)2 + a02− i² = (k_E0)2 − ³ ia0+ ² 2a0 ´₂ ここで a0 = pa2 + |kE|2 > 0 に注意すると、被積分関数の極は複素 k_E0 平面の第1象限と第3象限にあることが わかります。よって図20.1の積分経路 C1 を C2 に変形することができ、 弧にお ける積分は R → ∞ で消えるので、結果 k_E0 の積分範囲を −∞ ∼ +∞ に置き換 えることができます。これをウィック回転といいます。 図 20.1: ウィック回転 そうすると、簡単に確かめられる関係、 1 sc = 1 Γ(c) Z _∞ 0 dt tc−1e−st  (Re s > 0)

に注意して、 (左辺) = i Z d2ηkE (2π)2η 1 Γ(c) Z _∞ 0 dt tc−1e−(a2+kE2)t = i (2π)2η_Γ(c) Z _∞ 0 dt tc−1e−a2t Z d2ηkEe−k 2 Et = i (2π)2η_Γ(c) Z _∞ 0 dt tc−1e−a2t³π t ´_η = iπ η (2π)2η_Γ(c) Z _∞ 0 dt tc−η−1e−a2t = iΓ(c−η) (4π)η_Γ(c)a2(c−η)_. [証明終] 上の運動量積分公式で、kµ → kµ−bµ, a2 → a2+b2 とすれば、 Z d2η_k (2π)2η 1 (a2 _{+ 2b·k−k}2_−i²)c = iΓ(c−η) (4π)η_Γ(c) 1 (a2_+b2₎c−η_. これを辺々 bµ で微分して整理すれば、 Z d2ηk (2π)2η kµ (a2 _{+ 2b·k−k}2_−i²)c = iΓ(c−η) (4π)η_Γ(c) bµ (a2_+b2₎c−η_. 同様にさらに微分して整理すれば、 Z d2η_k (2π)2η kµ_kν (a2 _{+ 2b·k−k}2_−i²)c = i (4π)η_Γ(c) µ Γ(c−η)bµ_bν (a2_+b2₎c−η − Γ(c−η−1)gµν 2(a2_+b2₎c−η−1 ¶ が得られるでしょう。これら運動量積分公式はループグラフの計算で用います。

20.3

スカラー

4

乗模型とくりこみ因子

スカラー場 φ(x) に対し、スカラー4乗模型のラグランジアン密度は、 L = 1 2(∂φ) 2 ₋ m2 2 φ 2 ₋ λ 4!φ 4 でした。ここで m は φ 粒子の質量、λ は相互作用における結合定数ですが、この ように相互作用がある場合は、その影響で、質量、結合定数、さらには場のスケー ルがずれ、よってこれらの量は物理的に観測されるものとは一般に異なります。 そこで本来のラグランジアン密度を、改めて、 L = 1 2(∂φ0) 2 ₋ m20 2 φ 2 0 − λ0 4! φ 4 0

のように書きます。このとき m0 を裸の質量、λ0 を裸の結合定数、φ0(x) を裸の 場と呼びます。これらは物理的なものとは異なり、無限大である可能性もありま す。そして次のように、くりこまれた量 m, λ, φ を定義します。 φ0 = p 1 + ζφφ, m20 = 1 + ζm 1 + ζφ m 2_{, λ} 0 = 1 + ζλ (1 + ζφ)2 λ. ζφ, ζm, ζλ をくりこみ因子といいます。このときラグランジアン密度は、 L = 1 2(∂φ) 2 ₋ m2 2 φ 2 ₊ ζφ 2 (∂φ) 2 ₋ ζmm2 2 φ 2 ₋ λ(1 + ζλ) 4! φ 4 となるでしょう。くりこみ因子 ζi (i = φ, m, λ) を含む項を相殺項といいます。 図 20.2: 頂点のグラフ そうすると、ファインマングラフには図20.2のような頂点が存在することにな ります。(a)は2本の線が入る頂点で、流入する運動量を pµ として、 (a) = i 2(ζφp 2 _{− ζ} mm2). (b)は4本の線が入る頂点で、 (b) = −iλ(1 + ζλ) 4! です。(a)の式については、 ζφ 2 (∂φ) 2 ₋ ζmm2 2 φ 2 ₌ 1 2φ (−ζφ¤ − ζmm 2_{)φ + (} 全微分項) および、ファインマングラフの頂点において微分演算子 ∂µ は、頂点に流入する4 元運動量を pµ として ∂µ → −ipµ となることに注意すればわかるでしょう。 (余談) 一般に相互作用系では実はツリーレベルでもこのようなくりこみの処理を行っていて、 φ(x) はくりこまれた場で、m や λ はくりこまれた量です。しかしツリーレベルではくりこみ因子 の効果を無視して良いので、このことをあらわに意識することはなかったわけです。

20.4

頂点関数とくりこみ条件

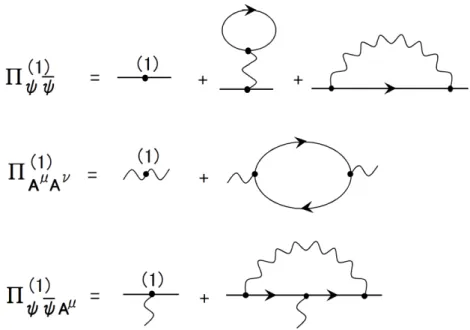
n 個 (n ≥ 2) の端点を持つ分離していないグラフがあって、どの内線を切って もグラフが分離しないとき、このグラフを1粒子既約であるといいます。このよ

うなグラフの外線を取り除いてできるグラフを全て足したものを n 点頂点関数と いい、Πφn と書きます。 頂点関数はファインマングラフの重要な構成単位になります。全てのファインマ ングラフは頂点関数を内線で繋いだものと考えることができます。ファインマン グラフを仮に自然数だとすると、頂点関数は素数のような役割を果たすわけです。 スカラー4乗模型の頂点関数を図20.3に示します。n が奇数のグラフはトポロ ジカルな理由により存在しないので、n が奇数のときは Πφn = 0 です。 図 20.3: 頂点関数 図 20.4: 相互作用の効果を含む内線 スカラー場の伝播関数の運動量表示、すなわち内線は、 ∆(p) = Z d4x < 0|T φ(x)φ(0)|0 > eip·x = i p2_−m2_+i²

ですが、相互作用と相殺項の効果を全て含む内線∆0(p)を考えると、これは図20.4 のように2点頂点関数を用いて展開されるので、 ∆0 = ∆ + ∆Πφ2∆ + ∆Π_φ2∆Π_φ2∆ + · · · = ∆ ∞ X n=0 (Πφ2∆)n = ∆ 1 − Πφ2∆ = 1 ∆−1_−Π φ2 = i p2_−m2_{+i² − iΠ} φ2 となります。ここでもし、くりこまれた質量 m や場 φ(x) が物理的なものなら、 ∆0_{(p) の極は p}2 _{= m}2_{−i² にあり、その留数は i になるだろうと考えられるので、} lim p2_{→ m}2_−i²(p 2_−m2_+i²)∆0_{(p) = i ∴ lim} p2_{→ m}2 Πφ2 p2_−m2 = 0. ここから、 Π_φ2|_p2_=m2 = 0, ∂ ∂p2 Πφ2|p2=m2 = 0 を得るでしょう。このような条件はくりこみ条件と呼ばれます。 同様に、くりこまれた結合定数 λ が物理的なものであるという要請から、4点 頂点関数について、 Πφ4|_p2 1=p22=p23=p24=m2 = −iλ ですが、実は4点頂点関数に流れ込む運動量 pµ₁, pµ₂, pµ₃, pµ₄ を全て質量殻上(p2_i = m2_{) においても、まだ p} i·pj に不定性が残ります。そこでここでは、4元運動量の 保存 pµ₁ + pµ₂ + pµ₃ + pµ₄ = 0 に注意して、 µ : pµ₁ = pµ₂ = −pµ₃ = −pµ₄ = (m, 0) をくりこみ点として、 Π_φ4|_µ = −iλ というくりこみ条件を設定します。 (余談) もし別のくりこみ点を取れば、散乱振幅や断面積の計算結果は変わってくるわけですが、 それは質量や結合定数をずらすことで他と一致します。質量や結合定数などの物理量は実験から 決まるいわゆるインプットパラメータであることを考えると、このことは本質的な違いではない わけです。ちなみに物理定数表などにある素粒子の質量や電荷の値は、無限遠方、すなわち低エネ ルギー極限における値を意味しています。

20.5

頂点関数のループ数展開

頂点関数 Πφn をフルに計算することは一般には不可能なので、何らかの分類に よる摂動計算が必要になります。ここではループ数展開というものを採用します。 つまり、グラフに含まれるループ数(未定運動量の数)で分類し展開するわけです。 Πφn = Π(0) φn + Π (1) φn + Π (2) φn + · · · .

Π(0)_φn は0ループ部分、すなわちツリー部分で、Π (1) φn は1ループ部分、Π (2) φn は2ルー プ部分、以下同様です。このとき同時に、くりこみ因子 ζi を、1ループ相当、2 ループ相当、· · · とみなした項で展開し、 ζi = ζi(1)+ ζ (2) i + · · · とします。ζ_i(m) はmループ相当の項で、これを頂点に持つグラフは、その頂点に mループがあるものとみなします。 そうすると、頂点関数のツリー部分と1ループ部分は図20.5のようになります。 頂点に(1)と書いてあるのはくりこみ因子1ループ相当の項を拾うことを意味して います。また、何も書いてない頂点はくりこみ因子を含まない項を拾うことを意 味します。 図 20.5: ループ数展開 2点頂点関数の1ループ部分 Π(1)_φ2 を考えてみましょう。それは、 Π(1)_φ2 = 2 · i 2(ζ (1) φ p2 − ζm(1)m2) + 4! 2 µ −iλ 4! ¶ Z d2η_k (2π)2η i k2 _{− m}2 _{+ i²} と表せます。時空の次元を2η としました。運動量積分公式により積分部分を計算 すると、 I = Z d2η_k (2π)2η i k2 _{− m}2 _{+ i²} = Γ(1 − η) (4π)η_(m2₎1−η_. 時空の次元は4なので、η = 2 − ² (² → 0) とすると、 I = m 2 16π2 Γ(−1 + ²)(4π) ²_(m2₎−² ですが、ここで、 Γ(−1 + ²) = Γ(²) −1 + ² = −Γ(²) (1 + ² + O(² 2_{)) = −(Γ(²) + 1 + O(²)),}

x² = e² log x = 1 + ² log x + O(²2) に注意すれば、 I = − m 2 16π2 µ Γ(²) + 1 + log 4π m2 + O(²) ¶ と評価されるので、結局、 Π(1)_φ2 = i(ζ (1) φ p2 − ζm(1)m2) + iλm2 32π2 µ Γ(²) + 1 + log 4π m2 ¶ です。よってくりこみ条件から、 ζ_φ(1) = 0, ζ_m(1) = λ 32π2 µ Γ(²) + 1 + log 4π m2 ¶ とくりこみ因子が定まり、この結果、 Π(1)_φ2 = 0 となります。lim ²→0Γ(²) は無限大ですが、それがくりこみ因子 ζ (1) m からの寄与と相 殺し、結果、頂点関数は有限になっていることに注意してください。ループグラ フによる補正は無限大、質量の補正は無限大で、これら無限大が打ち消しあって、 結果、全体の補正は有限というわけです。時空の次元を4からずらし発散する積分 をいったん有限化(正則化) して計算するこの方法は、次元正則化と呼ばれます。 次に4点頂点関数の1ループ部分 Π(1)_φ4 ですが、図20.5の第2項のループグラフ は、パラメータ公式と運動量積分公式を用いて次のように計算されます。 (4!)2 2 µ −iλ 4! ¶₂Z d2ηk (2π)2η i (k−p1)2−m2+i² i (k+p3)2−m2+i² = λ 2 2 Z d2ηk (2π)2η 1 m2_−(k−p 1)2−i² 1 m2_−(k+p 3)2−i² = λ 2 2 Z d2ηk (2π)2η Z ₁ 0 dx _³¡ 1 m2_−(k−p 1)2−i² ¢ x+¡m2_−(k+p 3)2−i² ¢ (1−x) ´₂ = λ2 2 Z d2η_k (2π)2η Z ₁ 0 dx _³ 1 m2_−xp2 1−(1−x)p23+2k· ¡ xp1−(1−x)p3 ¢ −k2_−i²´2 = λ 2 2 iΓ(2−η) (4π)η Z ₁ 0 dx ¡ 1 m2_{−x(1−x)(p} 1+p3)2 ¢_2−η = iλ2 32π2 Γ(²) (4π) ² Z ₁ 0 dx ¡m2−x(1−x)(p1+p3)2 ¢_−² = iλ 2 32π2 µ Γ(²) + log 4π m2 − I µ (p1+p3)2 m2 ¶¶ .

ここで I(s) = Z ₁ 0 dx log¡1−x(1−x)s¢. よって、 Π(1)_φ4 = − iλζ (1) λ + iλ2 32π2 Ã 3 µ Γ(²)+log 4π m2 ¶ −I µ (p1+p3)2 m2 ¶ −I µ (p1+p4)2 m2 ¶ −I µ (p1+p2)2 m2 ¶! ですが、くりこみ条件 Π(1)_φ4|µ = 0 から、I(0) = 0 に注意して、 ζ_λ(1) = λ 32π2 µ 3 µ Γ(²)+log 4π m2 ¶ − I(4) ¶ とくりこみ因子が定まり、 Π(1)_φ4 = − iλ2 32π2 µ I µ (p1+p3)2 m2 ¶ +I µ (p1+p4)2 m2 ¶ +I µ (p1+p2)2 m2 ¶ −I(4) ¶ を得ます。無限大である Γ(²) はやはりくりこみ因子により相殺しました。 6点以上の頂点関数の1ループの部分 Π(1)_φ6, Π (1) φ8, · · · が有限になることは、ルー プ運動量の次数を考えればわかるでしょう。 (余談) 一方で、例えばスカラー 5 乗模型 : L = 1 2(∂φ) 2₋m2 2 φ 2_{− kφ}5 _{(k は定数)} の 6 点頂点関数を考えると、図 20.6 のグラフが対数発散し、これを相殺する相殺項もありません。 すなわちスカラー 5 乗模型はくりこみ可能ではないわけです。結合定数 k は質量次元 −1 である ことがわかりますが、一般に結合定数が負の質量次元を持つ理論は、次元解析による分析からそ のくりこみ可能性が絶望的であることが知られています。ちなみにもし図 20.6 の発散を相殺しよ うとするなら、相殺項を用意するために φ6 の相互作用項の追加が必要です。しかしそうすると 7 点頂点関数や 8 点頂点関数が同様の理由で発散し、これを相殺するためにさらに φ7 や φ8 の相互 作用項の追加が必要となり、このようなことは永遠に続いてしまいます。 図 20.6: スカラー 5 乗模型の発散グラフ

20.6

散乱振幅の

2

次補正

スカラー4乗模型において φφ → φφ の散乱振幅を考えると、λの最低次(1次) は図20.7(a) により与えられ、M(1) = −iλ でした。 図 20.7: 散乱振幅の 2 次補正 λの2次の補正を考えると、それは図20.7(b)∼(g) のグラフの和になるでしょう。 これらグラフは12個ありますが、(c)と(d)は Π(1)_φ2 = 0 により相殺し、残ったグ ラフの和はちょうど Π(1)_φ4 に相当します。ただし散乱振幅においては p µ 3 と pµ4 が 頂点から出て行く方向に定義されるので、散乱振幅の2次補正は、 M(2) = − iλ 2 32π2 µ I µ (p1−p3)2 m2 ¶ +I µ (p1−p4)2 m2 ¶ +I µ (p1+p2)2 m2 ¶ −I(4) ¶ ということになります。 特に重心系においては、入射粒子の運動量を ±p. 散乱角を θ として、 (p1−p3)2 = −2|p|2(1−cos θ), (p1−p4)2 = −2|p|2(1+cos θ), (p1+p2)2 = 4(m2 + |p|2). また、 I(s) = Z ₁ 0 dx log¡1−x(1−x)s¢ =        r log r+1 r−1 − 2 (s < 0) r log 1+r 1−r − 2 + iπr (s ≥ 4).

ここで r = p1−(4/s) です。これらに注意して、重心系における散乱振幅の2次 補正は、 M(2) = − iλ 2 32π2 µ r1log r1+1 r1−1 + r2log r2+1 r2−1 − 4 + r3log 1+r3 1−r3 + iπr3 ¶ となります。ここで、 r1 = s 1 + 2m2 |p|2_{(1−cos θ),} r2 = s 1 + 2m2 |p|2_{(1+cos θ),} r3 = |p| p m2_+|p|2_. 計算の途中で現れる無限大はくりこみにより消え去り、有限の結果が得られまし た。微分断面積は、λ の1次においては等方的でしたが、2次の補正においては方 向依存性を持つことがわかります。

20.7

QED

のくりこみ

次に QED のくりこみについて見ておきます。QED のラグランジアン密度は、 ゲージ固定項を含めて、 L = ¯ψ(i/∂ − m)ψ − 1 4FµνF µν ₋ 1 2α(∂ ·A) 2 _{− qA} µψγ¯ µψ でした。ここでの定数と場を裸の量とみなし添字 0 を付けて表し、改めて、 ψ0 = p 1 + ζψψ, Aµ₀ = p 1 + ζAAµ, α0 = (1 + ζA)α, m0 = 1 + ζm 1 + ζψ m, q0 = 1 + ζq (1 + ζψ) √ 1 + ζA q でくりこまれた量(添字なし)を定義すると、 L = ¯ψ(i/∂ − m)ψ − 1 4FµνF µν ₋ 1 2α(∂ ·A) 2 + ζψψi/∂ψ − ζ¯ mm ¯ψψ − 1 4ζAFµνF µν _{− q(1 + ζ} q)Aµψγ¯ µψ のように、ラグランジアン密度に相殺項が付加されます。 これにより ψ ¯ψ に対応する頂点として i(ζψ/p − ζmm), また、 −iζA 4 FµνF µν ₌ iζA 2 A µ_(−∂ µ∂ν + gµν¤)Aν + (全微分項) に注意すると、AµAν に対応する頂点として (iζA/2)(pµpν− gµνp2). さらに、ψ ¯ψAµ に対応する頂点として −iq(1 + ζq)γµ が存在することがわかります。

ゲージパラメータは、くりこまれた量である α を、通常 1 にとります(ファイ ンマンゲージ)。このため裸のゲージパラメータ α0 は 1 からずれることに注意し てください。ゲージパラメータを導入しておく理由がここにあります。 (余談) QED くりこみの考案者は、ファインマン、シュウィンガー、朝永。次元正則化はトホー フト・ベルトマン (1972) によります。

20.8

QED

の頂点関数の有限性

QED の頂点関数で、1ループにおいて発散の危険性があるものはまずは図20.8 に示す3つです。これらがきちんと有限になることを見ておきましょう。 最初に Π(1)_{ψ ¯ψ} ですが、第1項は i(ζ_ψ(1)/p − ζm(1)m), 第2項のループグラフは、 Z d2η_k (2π)2η (−iqγµ) −igµν i² (−1)tr µ (−iqγν) i(/k + m) k2 _{− m}2 _{+ i²} ¶ であり、非常に特異性の強いグラフですが、/k の項は奇関数の積分であることか ら消え、そうするとtr(γν) = 0 であることからこの式は 0 であるとわかります。 一方、第3項のループグラフは、パラメータ公式と運動量積分公式を用いて、 Z d2η_k (2π)2η(−iqγµ) i(/p − /k + m) (p−k)2 _{− m}2 _{+ i²}(−iqγν) −igµν k2 _{+ i²} = −2q2 Z d2η_k (2π)2η Z ₁ 0 dx¡ /k − /p + 2m (m2_−p2_{)x + 2xp·k − k}2 _{− i²}¢2 = iq2 16π2 Γ(²)(/p − 4m) + O(1) と評価されます。ここで O(1) は ² の0次以上の項、すなわち ² → 0 で有限に留 まる項です。よって、 ζ_ψ(1) = − q 2 16π2 Γ(²) + O(1), ζ (1) m = − q2 4π2 Γ(²) + O(1) とすることにより Π(1)_{ψ ¯ψ} は有限になります。 次に Π(1)_Aµ_Aν ですが、第1項は iζ_A(1)(p_µp_ν − g_µνp2), 第2項のループグラフは、 Z d2η_k (2π)2η (−1)tr µ (−iqγµ) i(/k + m) k2 _{− m}2 _{+ i²}(−iqγν) i(/k − /p + m) (k−p)2 _{− m}2 _{+ i²} ¶ = −4q2 Z d2η_k (2π)2η Z ₁ 0 dx2kµkν−gµνk 2_−p µkν−pνkµ+gµνp·k+gµνm2 ¡ m2 _{− xp}2 _{+ 2xp·k − k}2 _{− i²}¢2 = iq2 12π2 Γ(²)(pµpν − gµνp 2_{) + O(1)}

図 20.8: QED の頂点関数 と評価され、上手い具合に発散部分が (pµpν − gµνp2) に比例します。よって、 ζ_A(1) = − q 2 12π2 Γ(²) + O(1) とすることで Π(1)_Aµ_Aν は有限になります。ゲージ場は質量を持たないため、ゲージ 場の2点頂点関数に存在するくりこみ因子は ζ_A(1) の1つだけであり、無限大の相 殺が危ういのですが、実際にはこのように上手くいくのです。これはゲージ理論 の奇跡の一端といえます。一般に非可換ゲージ理論(ヤン・ミルズ理論)を含め、 ゲージ理論はくりこみ可能であることが知られています。 最後に Π(1)_{ψ ¯ψA}µ ですが、第1項は −iqζ (1) q γµ, 第2項のループグラフを Lµ とおき ましょう。流入する運動量を pµ₁, pµ₂, pµ₃ とおくと、pµ₁ + pµ₂ + pµ₃ = 0 なので、Lµ は pµ₁ と pµ₂ の関数です。これらの変数で展開して、 Lµ = Lµ|_pµ 1=pµ2=0 + p ν 1 ∂Lµ ∂pν 1 ¯ ¯ ¯ ¯ pµ₁=pµ₂=0 + pν₂ ∂Lµ ∂pν 2 ¯ ¯ ¯ ¯ pµ₁=pµ₂=0 + · · · . ところが Lµ の被積分関数はループ運動量の −4 次なので、すでに対数発散でし かなく、これを流入運動量で1回でも微分すれば収束するはずです。すなわち上 の展開式で発散するのは右辺第1項だけであり、それは、 Z d2η_k (2π)2η (−iqγρ) i(/k + m) k2 _{− m}2 _{+ i²}(−iqγµ) i(/k + m) k2 _{− m}2 _{+ i²}(−iqγσ) −igρσ k2 _{+ i²} = − iq 3 16π2 Γ(²)γµ+ O(1)

と評価されます(∗)。よって、 ζ_q(1) = − q 2 16π2 Γ(²) + O(1) とすることで Π(1)_{ψ ¯ψA}µ は有限になるわけです。 この他、Π(1)_Aµ_Aν_Aλ やΠ (1) Aµ_Aν_Aρ_Aσ なども発散する危険性がありそうに見えますが、 Π(1)_Aµ_Aν_Aλ は図20.9に示すフェルミオンの三角ループグラフ2つから成り、これら は相殺し消えてしまいます(後述)。一方、Π(1)_Aµ_Aν_Aρ_Aσ は 3! = 6 つの四角ループグ ラフ(ボックスグラフ) からなり、やはり有限になることが知られています。頂点 が5個以上あるフェルミオンループはループ運動量の次数を考えればわかるよう に、収束します。 図 20.9: 三角ループグラフ (*注) ここでの計算には、 Z d2η_k (2π)2η kµ_kν (k2_{+ i²)(k}2_{− m}2_{+ i²)}2 = iΓ(²)gµν 64π2 + O(1) という積分公式を用いるのがてっとり早いです。証明ですが、この積分を Iµν とすると、Iµν = Cgµν と書けるはずですが、このとき、 I_µµ = 2ηC = Z d2η_k (2π)2η 1 (k2_{− m}2_{+ i²)}2 = iΓ(²) 16π2 + O(1) が運動量積分公式からすぐにわかります。よって C = iΓ(²) 64π2 + O(1) です。

20.9

ファリーの定理

一般にQEDにおいては、正の奇数 n に対し、電磁場のn点頂点関数の1ループ 補正は正確に0になります。これをファリーの定理といいます。 証明ですが、まず電磁カレント jµ(x) = ¯ψ(x)γµψ(x) が荷電共役変換 C に対し て、(jµ(x))C = Cjµ(x)C−1 = −jµ(x) と符号を変えること、および C|0 > = |0 > に注意すると、正の奇数 n に対し、 < 0|T jµ1(x 1)jµ2(x2) · · · jµn(xn)|0 > = 0 (∗)

がわかります。なぜなら左辺は、カレントとカレントの間、およびカレントと真 空の間に C−1C = 1 を挟めば、n が奇数のとき符号が変わるからです。 n = 1 のとき(∗)は、 < 0|T ¯ψ(x)γµψ(x)|0 > = 0 ∴ tr(γµ∆(0)) = 0. ここで、 ∆(x−x0) = < 0|T ψ(x) ¯ψ(x0)|0 > = Z d4k (2π)4 i(/k + m) k2 _{− m}2 _{+ i²} e −ik·(x−x0₎ はフェルミオンの伝播関数です。この結果はすでに Π(1)_{ψ ¯ψ} の第2項の評価で見た通 りです。 n = 3 のとき(∗)は、 < 0|T ¯ψ(x1)γµ1ψ(x1) ¯ψ(x2)γµ2ψ(x2) ¯ψ(x3)γµ3ψ(x3)|0 > = 0 ですが、ウィックの定理で展開し、n = 1 の結果に注意すれば、 tr¡γµ1∆(x 1−x2)γµ2∆(x2−x3)γµ3∆(x3−x1) ¢ +tr¡γµ1_∆(x 1−x3)γµ3∆(x3−x2)γµ2∆(x2−x1) ¢ = 0 を得ます。左辺はちょうど Π(1)_Aµ1_Aµ2_Aµ3, すなわち三角ループグラフ2つの和(その 空間表示) に比例していて、それが0だというわけです。 以下、n = 5, n = 7, · · · においても同様のことを示すことができ、よってファ リーの定理がいえます。

20.10

シュレーディンガー場のくりこみ

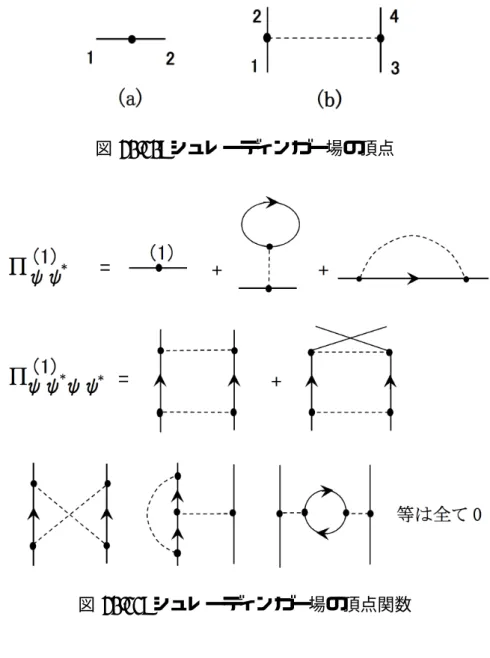
最後に非相対論的な場の量子論であるシュレーディンガー場の量子論のくりこ みについて見ておきましょう。 シュレーディンガー場を ψ(x) として、作用は、 S = Z d4x ψ†(x) µ i∂t + 1 2m4 ¶ ψ(x). m は粒子の質量を意味します。場の方程式、および正準交換関係(フェルミオンの 場合は反交換関係)は、 µ i∂t + 1 2m 4 ¶ ψ(x) = 0, [ ψs(x), ψ∗s0(x0) ]_t=t0 = δ_ss0δ3(r−r0)

となり、他は同時刻(反)可換です。一般解は、 ψs(x) = Z d3_k (2π)3 cs(k) e ik·r−i²(k)t_{, ²(k) =} |k|2 2m となり、ここで、 _£ cs(k), c∗s0(k0) ¤ = (2π)3δss0δ3(k−k0). 他は(反)可換です。伝播関数は、 < 0| T ψs(x)ψs∗0(x0)|0 > = θ(t−t0) < 0|ψ_s(x)ψ_s∗0(x0)|0 > = Z dω 2πi 1 ω−i²e iω(t−t0₎ δss0 Z d3_k (2π)3 e ik·(r−r0_{)−i²(k)(t−t}0₎ = Z dωd3_k (2π)4 iδss0 −ω+i²e ik·(r−r0_{)−i(²(k)−ω)(t−t}0₎ = Z d4_k (2π)4 iδss0 k0_−²(k)+i²e −ik·(x−x0₎ のように計算されます。途中、k0 = ²(k) − ω で積分変数を置換しました。よって ファインマングラフにおける粒子の内線は、粒子の4元運動量を (k0, k) として、 iδss0/(k0 − ²(k) + i²) です。 以上の自由場の理論に次の相互作用項を付加します。 SI = −V Z d4x ψ†(x)ψ(x) − 1 2 Z d4xd4x0G(x−x0)ψ†(x)ψ(x)ψ†(x0)ψ(x0). ここで V は定数の外部ポテンシャルを意味します。また、自己相互作用として クーロン力だけがあるとし、 G(x) = q 2_δ(t) 4π|r| = Z d4_k (2π)4 q2 |k|2 e −ik·x とします。q は粒子の電荷を意味します。このときファインマングラフには図20.10 に示す2つの頂点が存在し、それぞれ、 (a) = −iV δs1s2, (b) = −iq2 |k|2 δs1s2δs3s4 ということになります。ここで k は点線部(仮想光子)の運動量を意味します。 外部ポテンシャル V をループ数で展開し、V = V(1)+ V(2)+ · · · としましょう。 そうすると、2点頂点関数の1ループ部分 Π(1)_ψψ∗ は図20.11のように与えられます が、簡単のためスピン0のボゾンの場合を考えると、第1項は −iV(1). 第2項は、 −iq2 |0|2 Z d4_k (2π)4 i k0_−²(k)+i² = −iq2 2|0|2 Z d3_k (2π)3_.

図 20.10: シュレーディンガー場の頂点 図 20.11: シュレーディンガー場の頂点関数 第3項は、流入する運動量を p として、 Z d4_k (2π)4 i k0_−²(k)+i² −iq2 |k−p|2 = −iq2 2 Z d3_k (2π)3 1 |k|2 と評価されます。ここで簡単に確かめられる積分公式 : Z _∞ −∞ dx x − ia = ( +iπ (a > 0) −iπ (a < 0) を用いて、それぞれの k0 積分を実行しました。第2項と第3項は共に無限大です が、これらを V(1) によりくりこんで、 Π(1)_ψψ∗ = 0 とおくことができます。第2項も第3項も流入する4元運動量 (p0, p) に依存しな いため、恒等的に上式を仮定でき、くりこみ点の概念は必要ありません。これは 非相対論的な場の量子論の特徴といえます。

4点頂点関数 Π(1)_ψψ∗_ψψ∗ については、ループに沿って内線が同じ向きになるグラ フが、 Z dk0 1 k0 _{+ A + i²} 1 k0 _{+ B + i²} = 1 B − A Z dk0 µ 1 k0 _{+ A + i²} − 1 k0 _{+ B + i²} ¶ = 0 という機構により全て消えるので、図20.11に示すように2つの梯子グラフだけか ら成り、これらは有限であることが確かめられます。 QEDがくりこみ可能であれば、その近似理論であるシュレーディンガー場の量 子論(+クーロン相互作用)がくりこみ可能である必要はないわけですが、このよ うに少なくとも1ループにおいてはくりこみが可能で、正しい補正計算を行うこ とができるわけです。

索 引

あ 1 粒子既約 . . . 6 ウィック回転 . . . 4 運動量積分公式 . . . 4 か くりこみ因子 . . . 6 くりこみ条件 . . . 8 くりこみ点 . . . 8 くりこみ理論 . . . 3 さ 次元正則化 . . . 10 相殺項 . . . 6 た 頂点関数 . . . 7 は 裸の結合定数 . . . 6 裸の質量 . . . 6 裸の場 . . . 6 パラメータ公式 . . . 3 ファインマンのパラメータ公式 . . . 3 ファリーの定理 . . . 16 や ユークリッド化 . . . 4 ら ループ数展開 . . . 8