r 1 m A r/m i) t ii) m i) t B(t; m) ( B(t; m) = A 1 + r ) mt m ii) B(t; m) ( B(t; m) = A 1 + r ) mt m { ( = A 1 + r ) m } rt r m n = m r m n B

(1)

第

1

章極限と導関数

1.1 数列と極限

例題１：複利の極限としての連続複利

¶ ³ 1 年間の金利を r とする．1 年間を m 期間に等分し，元本 A 円を毎期複利で運用するものとする．各期の金利は r/m である． i) t 年後にはいくらになっているか． ii) m を無限大にするとどうなるか． µ ´ i) t 年後の金額を B(t; m) とする． B(t; m) = A³1 + r m ´mt ii) B(t; m) を以下のように変形する． B(t; m) = A³1 + r m ´mt = A ¯³ 1 + r m ´m r °rt ここで n =m_r とおくと，m → ∞ のとき，n → ∞ なので，B(t; m) → Aertとなる．ただし，次の公式を用いた． e ≡ lim n!1 µ 1 + 1 n ¶n (1.1) ¥ e は，自然対数の底，あるいはネイピア数と呼ばれる．

数列

a1, a2, a3, . . . と無限に続く数の列を数列と呼ぶ．これを {an} と表記することもある． n を無限に大きくしていくにしたがい，数列がある一定の値にずっと近づいていくことがある．この値が α だとすると，α を数列 {an} の極限と呼び．数列 {an} は α に収束するという．これを n → ∞ のとき an→ α (1.2) と書く．あるいは，記号を用いて， lim n!1an= α (1.3) と表す．必ずしもすべての数列が収束するとは限らない．

(2)

例 1.1 an= ₂1n とする．limn!1an= 0 である．例 1.2 an= 2nとする．n を大きくすると，anも限りなく大きくなる．n → ∞ のとき anも ∞ となる．この場合，{an} は発散するという．例 1.3 an= (−1)nとする．anは，n が偶数の時 1，奇数の時 −1 となり一定の値には収束しない．

収束の判定法

等比数列定数 a0と定数 r を用いて，an = a0rnと表される数列を等比数列という．|r| < 1 のとき limn!1an= 0 である．|r| > 1 のとき {an} は発散する．一般の場合でも，次の定理が成り立つ．定理 1.1 limn!1|a_an+1_n | < 1 ならば，limn!1an= 0 となる． ¥ 有界で単調な数列数列 {an} が上に有界とは，任意の n について an≤ β となる定数 β が存在すること．数列 {an} が下に有界とは，任意の n について an≥ γ となる γ が存在すること．数列 {an} が有界とは，数列 {an} が上にも下にも有界であること．任意の n について an≤ an+1ならば，数列 {an} は単調増加であるといい，任意の n について an≥ an+1ならば，数列 {an} は単調減少であるという．定理 1.2 上に有界な単調増加数列は収束する．下に有界な単調減少数列は収束する． ¥

極限の性質

定理 1.3 数列 {an} と数列 {bn} が収束し，limn!1an= a，limn!1bn= b であるとする． 1) {an+ bn} は収束し，limn!1(an+ bn) = a + b である． 2) {anbn} は収束し，limn!1(anbn) = ab である． 3) {an/bn} は収束し，limn!1(an/bn) = a/b である．ただし，b 6= 0 とする． 4) 任意の n について an≤ bnならば，a ≤ b である． ¥ 演習問題 1.1 anが次の式で与えられる場合，数列 {an} の収束を判定せよ．収束するならば，極限を求めよ． 1) (−1/2)n ₂₎√_{n + 1 −}√_n ₃₎ n + 1 n 4) n 3n

(3)

1.2 級数

数列 {an} の第 n 項までの和を Snとする． Sn= a0+ a1+ a2+ · · · + an {Sn} はそれ自身数列となり，(無限) 級数と呼ばれる．Snを第 n 部分和と呼ぶ．{Sn} が収束し， limn!1Sn= s となるとき，s を級数の和と呼ぶ．経済学／経営学において重要なのは，次の式で与えられる級数である． Sn= 1 + r + r2+ · · · + rn (1.4) これを等比級数という．Sn− rSnを計算すれば容易にわかるように，(1.4) は次のように書き換えることができる． Sn= 1 − r n+1 1 − r (1.5) ただし r 6= 1 とする． (1.5) から級数の和について，次のことがわかる． |r| < 1 のとき， lim n!1Sn= 1 1 − r

例題２：乗数効果

¶ ³ 限界消費性向 (家計の追加的所得に対して，消費にまわる比率) が r であるとする．政府支出を A 円増加させると，総需要はいくら増加するか． µ ´ 政府支出の増加分 A が，所得を押し上げる．増加分 A のうち，Ar が消費に回る．この消費の増加が再度所得の増加となり，Ar2の消費につながる．これが，無限に続くと考えると，全体の需要の変化 ∆Y は， ∆Y = A + Ar + Ar2_{+ Ar}3_{+ · · ·} で与えられる．0 < r < 1 より，この級数は収束し，その和は A_1−r1 で与えられる． ¥

(4)

1.3 導関数

x と y の関係が，ある関数 f(x) として与えられているとする．このとき，x が変化したとき，y がどれくらい変化するかは，x と y の関係を知る上でたいへん重要なことである．以下では，まず 1 変数の関数について考える．多変数関数は 2 章で扱う．

1 次関数

y = ax + b のかたちで表現できる関数を考える．x = x0のとき，y = ax0+ b (≡ y0) である． x0から x0+ ∆x に変化したとき，y の変化量は， ∆y =¡a(x0+ ∆x) + b ¢ − (ax0+ b) = a∆x となる．したがって，その変化量の比は， ∆y ∆x = a∆x ∆x = a となり，∆x や x0に依存しない定数となる．

2 次関数

2 次関数として y = x2_{+ 2x + 4 を考える．x = 2 のとき，y = 4 である．x の変化にたいする y} の変化を知りたいので，∆x をいくつか変えて，そのときの y の変化量と変化率 (∆y/∆x) を計算した．図表 1.1 y = x2+ 2x + 4 ∆x ∆y ∆y/∆x 2 16 8 4 40 10 6 72 12 Y X 0.0000 20.0000 40.0000 60.0000 80.0000 100.0000 120.0000 0.0000 2.0000 4.0000 6.0000 8.0000 10.0000 図表 1.1 からわかるように，2 次関数の場合，変化率は ∆x に依存する．そこで，∆x に依存しないように変化率を考えるため，関数の接線の傾きをその接点における変化率と定めることにす

(5)

る．接線の傾きは，∆x を限りなく 0 に近づけたときの変化率の極限と考えられる．x = 2 における変化率は，∆x を用いて， (2 + ∆x)2_{+ 2(2 + ∆x) + 4 − (2}2_{+ 2 ∗ 2 + 4)} ∆x = ∆x2_{+ 6∆x} ∆x = ∆x + 6 と書ける．∆x → 0 のとき ∆x + 6 → 6 である．

一般の場合

ある点 x0における変化率の極限は，(存在すれば) 次の式で与えられる． lim h!0 f(x0+ h) − f(x0) h (1.6) これは，x0における f(x) の微分係数と呼ばれる．微分係数は (もし存在すれば)x0に対応して値が定まるので，x0と微分係数の関係を一つの関数ととらえることができる．この関数をもとの関数から導かれたという意味で，導関数と呼ぶ．y = f(x) の導関数は，次のように表記する． y0 _f0_(x) dy dx df dx 導関数を求めることを微分するという．

微分可能

すべての関数が微分できるとは限らない．微分係数が存在しない場合があるからである．連続関数と不連続関数関数 f(x) が点 a で連続であるとは，次の条件が成り立つことである． f(a) = lim x!af(x) この条件が満たされないとき，x = a で f(x) は不連続であるという．関数が不連続な点では微分できない．なめらかな関数 x = a における変化率の極限を求めるとき，点 a に上から近づくか下から近づくかで収束先が異なる場合がある． lim h!0 h>0 f(a + h) − f(a) h 6= limh!0 h<0 f(a + h) − f(a) h のとき，f(x) は x = a で微分可能ではない．演習問題 1.2 y = |x| は，= 0 で微分不可能である．limh!0 h>0 |0+h|−|0| h ，および limh!0_h<0 |0+h|−|0| h を求めることにより，それを示せ．

(6)

接線の方程式

関数 y = f(x) の点 x0における接線を求める．接線の方程式を y = ax + b とおく．接線なので， y0= ax0+ b = f(x0) (1.7) を満たす．x0から h だけ変化した点 x0+ h では，接線ともとの関数の値は異なる．その差を ²(h) とおく．すなわち， f(x0+ h) = a(x0+ h) + b + ²(h) (1.8) である．変化率を計算すると， ∆y ∆x = f(x0+ h) − f(x0) x0+ h − x0 = (ax0+ ah + b + ²(h)) − (ax0+ b) h = ah + ²(h) h = a + ²(h) h 接線の傾きは微分係数に他ならないので，a = f0(x0) である．また limh!0 ²(h)_h = 0 となる ²(h) が存在することを微分可能の条件と考えてもよい．

関数の増減

ある点で関数が増加しているか減少しているかは，その点における接線の傾きを見ればわかる．接線の傾きが正であれば関数は増加しており，負であれば関数が減少している．接線の傾きは微分係数なので，導関数の符合により関数の増減を判定できる．単調増加関数：関数 f(x) が単調増加であるとは，任意の x1> x2において，f(x1) ≥ f(x2) が成り立つこと．単調減少関数：関数 f(x) が単調減少であるとは，任意の x1> x2において，f(x1) ≤ f(x2) が成り立つこと．上の不等式が，狭義になりたつとき，それぞれ狭義単調増加関数，狭義単調減少関数という．任意の x において f0(x) ≥ 0 ならば，f(x) は単調増加関数である．任意の x において f0_{(x) ≤ 0} ならば，f(x) は単調減少関数である．

平均値の定理

¶ ³ f(x) が開区間 (a, b) で微分可能，閉区間 [a, b] で連続ならば f(a) − f(b) = f0(c)(b − a) を満たす c ∈ (a, b) が存在する． µ ´

(7)

1.4 微分の基本法則

基本的な関数の微分

i) 定数関数： a を定数とする．f(x) = a は，どの x に対しても常に一定の値 a をとる定数関数である．これを微分すると， f0_{(x) = 0} である． ii) 多項式： n を自然数，an, an−1, . . . , a1, a0を実数とすると， f(x) = anxn+ an−1xn−1+ · · · + a1x1+ a0 の形で表現できる関数を n 次多項式と呼ぶ．この関数の導関数は， f0_{(x) = a} nnxn−1+ an−1(n − 1)xn−2+ · · · + a1 である． iii) 冪関数： f(x) = xn_{を冪関数という．n は任意の実数でよい．} f0_{(x) = nx}n−1 n は任意の実数でよいので，√x = x12 _や 1 x = x−1の微分もこの公式に従う． iv) 指数関数： f(x) = ex_{を (e を底とする) 指数関数と呼ぶ．指数関数の導関数は次の通り．} f0(x) = ex すなわち，指数関数は微分しても関数形が変化しない． v) 対数関数自然対数を底とする対数関数 f(x) = log の導関数は f0_{(x) =} 1 x である．

関数の和と差の微分

二つの関数 f(x) と g(x) の和によって定義される関数の微分は， ¡ f(x) + g(x)¢0= f0(x) + g0(x) である．f(x) と g(x) の差によって定義される関数の微分は， ¡ f(x) − g(x)¢0= f0(x) − g0(x) である．

(8)

関数の積の微分

二つの関数 f(x) と g(x) の積によって定義される関数の微分は， ¡ f(x)g(x)¢0= f0(x)g(x) + f(x)g0(x) である．

合成関数の微分

y = f(u)，u = g(x) とする．このとき h(x) = f(g(x)) を，f と g の合成関数という．h(x) の導関数は，次の式で与えられる． dh dx = df du dg dx

逆関数の微分

集合 X と集合 Y の要素の間に対応関係があり，それを関数 f を使って y = f(x) と表す．関数 f が次の性質を満たすとする． i) 任意の y ∈ Y について，y = f(x) となる x ∈ X が存在する． ii) 任意の x1, x2∈ X について，x16= x2ならば f(x1) 6= f(x2) となる．このとき，関数 f に逆関数 f−1が存在し，y = f(x) を満たす任意の (x, y) ∈ X × Y について， x = f−1_{(y) となる．} y = f−1_{(x) の導関数は，次のように表すことができる．} ¡ f−1_(x)¢0₌ 1 f0_(x) 演習問題 1.3 次の関数の導関数を求めよ． (1) 3x3_{+ x}2_{− x + 5 (2) e}3x+2 _{(3) xe}x ₍₄₎ 3x+2 x+3 (5) q 1 x (6) ax (7) logax 演習問題 1.4 次の関数の逆関数の導関数を求めよ． (1) x + ex _{(2) x}2_{+ 3 (ただし x > 0 とする)}

(9)

1.5 高次の導関数とテーラー展開

n 階導関数

関数 f(x) の導関数が微分可能なとき，再度微分することで 2 階の導関数が得られる．それを， f00_(x), _f(2)_(x), d2f dx2 などと表記する．一般の n について，n − 1 階までの導関数が微分可能であれば，f(x) は n 回微分可能であるという．n 階の導関数は，以下のように表記する． f(n)_(x), dnf dxn

テーラーの定理

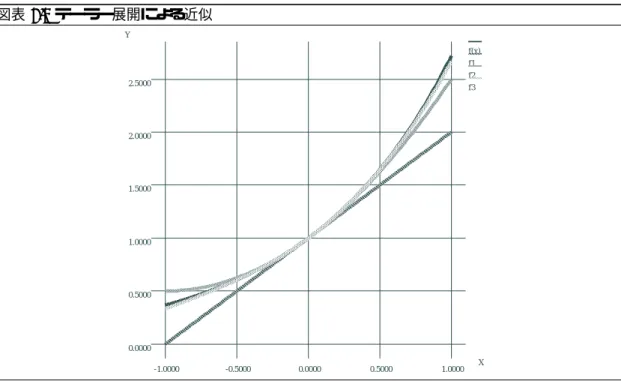
n 回微分可能な関数 f(x) にたいして， f(x) = f(a) +f 0_(a) 1! (x − a) + f00_(a) 2! (x − a) 2₊f(3)(a) 3! (x − a) 3_{+ · · · +}f(n−1)(a) (n − 1)! (x − a) (n−1)_{+ R} n(x) で，Rn(x) を定義する．このとき， Rn(x) = f (n)_(c) n! (x − a) n となる c が存在する． ¥ f(x) が a を含む区間 I で ∞ 回微分可能で，I 上の x において limn!1Rn(x) = 0 ならば， f(x) =P1_n=0 fn_n!(x)(x − a)n_{と表すことができる．これを，f(x) の a を中心とするテーラー展開と} いう．テーラー展開は，関数を多項式で近似する方法を与える．例 1.4 f(x) = ex_{とする．x = 0 のまわりでテーラー展開すると，(e}x₎(n)_{= e}x _より， ex= e0+ e 0 1!(x − 0) + e0 2!(x − 0) 2_{+ · · · +}e0 n!(x − 0) n_{+ · · ·} = 1 + 1 1!x + 1 2!x 2_{+ · · · +} 1 n!x n_{+ · · ·} 例 1.5 f(x) = ex_{の x = 0 におけるテーラー展開を第２，３，４項までとると，それぞれ 1 次，2 次，3 次} 近似となる (図 1.3 参照)． f1(x) = 1 + x f2(x) = 1 + x +1 2x 2 f3(x) = 1 + x +1 2x 2₊1 6x 3

(10)

図表 1.2 テーラー展開による近似 f(x) f1 f2 f3 Y X 0.0000 0.5000 1.0000 1.5000 2.0000 2.5000 -1.0000 -0.5000 0.0000 0.5000 1.0000

1.6 弾力性と成長率

関数 f(x) の x = x0における弾力性 ε(x0) を，次のように定義する． ε(x0) = xf 0_(x) f(x)

例題３：価格弾力性

¶ ³ ある財の，価格 p における需要が f(p) = _p42 で与えられているとする．p = 1 と p = 4 における限界需要と価格弾力性を求めよ． µ ´ 価格 p における限界需要は， f0(p) = − 8 p3 で与えられるので，p = 1 における限界需要は −8，p = 4 における限界需要は −1/8 となる．一方，価格 p における価格弾性値は， ε(p) = xf 0_(x) f(x) = −2 なので，p の値によらず −2 である． ¥

(11)

例題４：成長率

¶ ³ ある商品のマーケットシェア y が年々増加していることがわかった．適当な近似により y を時間 t の関数として f(t) = _1+e1−t と表すことができるものとする．t = 0.5 におけるマーケットシェアの成長率を求めよ． µ ´ 成長率とは，微少時間 ∆t における y の変化（∆y）の，y に対する比率の極限をとったものである．すなわち， lim ∆t!0 ∆y ∆t y = 1 f(t)∆t!0lim f(t + ∆t) − f(t) ∆t = f0_(t) f(t) で与えられる．f0(t) = e−t (1+e−t₎2 より，成長率は f0_(t) f(t) = − e−t (1 − e−t₎2 ∗ (1 + e −t_{) =} e−t 1 + e−t となる．よって，t = 0.5 においては，成長率は_1+ee−0.5−0.5 ≈ 0.378 である． (log f(x))0 ₌ f0_(x) f(x) なので，成長率の導出にはこの関係を用いてもよい． ¥ 図表 1.3 ロジステックス曲線 Y x 10-3 t 200.0000 400.0000 600.0000 800.0000 -3.0000 -2.0000 -1.0000 0.0000 1.0000 2.0000 3.0000 演習問題 1.5 y が時間 t の関数として，y = et_{によって与えられているとする．y の成長率を求めよ．}