127
第
5
章 シミュレーション
—
現実を模倣する
現実に起きたことは一度きりの出来事であって,物理や化学実験のように条件を かえて繰り返し行うことはできません.しかし,適切な方法で現実をモデルに置 き換えて表現することによって,条件の変化とその結果について繰り返し調べ ることができます.これは,現実をシミュレートするという意味で,シミュレー ションと呼ばれています.特に計算機上で乱数を発生させて,その結果を統計的 な処理を加えて分析する確率的シミュレーションは,不確実性を評価するための 有力な手法です.5.1
乱数
確率的シミュレーションでは,乱数を用いて不確実性を表現します.具体的な例で説明しましょ う.商品の需要は,事前に予測することは困難です.一人一人の消費者がある商品を買う/買わな いの判断を行うには相応の理由があるわけですが,集計された売り上げを個々の消費者の心理に 遡って説明することは事実上不可能であり,売り手に取って不確実な数値とならざるを得ません. 経済・経営学で不確実性を取り扱う代表的な方法は,それを確率変数とみなすことです. 需要を確率変数とみなすとは,おおざっぱに言えば,需要がどのような値 (実現値) をとるか, およびその値をとる確率がいくらか,の 2 つを評価できることを意味します.例えば,次のような 場合です.需要 X が離散的な分布をするときは, X= 10, 確率 : 0.25 5, 確率 : 0.6 2, 確率 : 0.15 (5.1) などと表現できます.また,連続的な分布をする場合,例えば X が平均 1/6 の指数分布にしたが う場合は, Pr{X ≤ x} = 1 − e−6x, x≥ 0 (5.2) などと書けます. 利益 Y が需要 X の関数として表現できたとしましょう.つまり需要が x であったとして,利益 が f(x) となる場合です.需要 X が確率変数ならば,その関数である利益 Y = f(X) も確率変数とな ります.もし f が簡単な関数であれば,直接その分布を評価することができます. f(x) = 3x − 10だったならば,(5.1) の場合, Y= 3∗ 10 − 10 = 20, 確率 : 0.25 3∗ 5 − 10 = 5, 確率 : 0.6 3∗ 2 − 10 = −4, 確率 : 0.15 (5.3)となり,(5.2) の場合, Pr{Y ≤ y} = Pr{3X − 10 ≤ y} = Pr{X ≤ 1 3(y + 10)} = 1 − e −6(1 3(y+10)) = 1 − e−2y−20, y≥ 0 (5.4) となります. f(x) = 3x − 10が複雑な関数になると,(5.3)(5.4) のように Y の分布を陽に求めるのが困難にな ります.上の例では,不確実性は需要のみでしたが,多くのパラメータに不確実性が存在すると, 結果の評価はさらに難しくなります.そのような場合でも,乱数を用いて利益 Y の挙動を調べる ことが可能です.X の分布がわかっているならば,その分布にしたがうように乱数値 x を発生させ て,その数値 x にもとづいて f(x) を求めます.多数の乱数を発生させることで,結果として Y の 分布を求めることができます. 乱数は,サイコロをふるなどの手作業によって生成する方法もあります.また乱数表として与 えられている場合もあります.一般に多く用いられるのは,計算機上で一定の数式に基づいて乱数 を計算する方法です. 図表 5.1 X の分布の例
5.2
PERT
の例
5.2.1
作業時間の変動
2.9節(85 ページ)で,PERT を学びました.その際は作業時間の変動について簡単にまとめた だけでしたが,ここでシミュレーションを利用した分析を行ってみます.まず例として,図表 5.2 にあるような A∼F の 6 つの作業からなるプロジェクトを考えましょう. プロジェクト・ネットワーク図およびクリティカル・パス(太線)は図表 5.3 にある通りです. 図表 5.3 には,各作業の最早開始時刻,最遅完了時刻,余裕時間も記入してあります. 作業時間が変化した場合をみてみましょう.図表 5.2 をケース1として,さらに三組の異なる作 業時間が図表 5.4 で与えられたならば,その結果は図表 5.5 の三つの図で表されます.それぞれの5.2. PERTの例 129 図表 5.2 先行作業と平均作業時間 作業 先行作業 作業時間 A — 6 B — 4 C — 6.2 D A 2 E A,B,C 4.5 F B,C 4 図表 5.3 時間分析の結果(作業時間 [最早開始時刻,最遅完了時刻,余裕時間])
S
A
B
C
D
E
F
T
0[0,0,0] 6[0,6.2,0.2] 2[6,10.7,2.7] 4[0,6.2,2.2] 6.2[0,6.2,0] 4.5[6.2,10.7,0] 4[6.2,10.7,0.5] 0[10.7,10.7,0] case 1 ケースについて,プロジェクトの完了時刻やクリティカルパスが異なっていることがわかるでしょ う.しかし,わずか 4 つの例だけでは,体系的な情報としてまとめるには不十分です. 図表 5.4 作業時間の変化 作業時間 作業 ケース1 ケース2 ケース3 ケース4 A 6 4 8 4 B 4 5 3 3 C 6.2 5.2 5.2 5.2 D 2 3 1 3 E 4.5 5.5 3.5 5.5 F 4 6 6 25.2.2
作業時間の分布
前節では,作業時間の変化について 4 つのケースでみてみました.ここで,作業時間の変動に ついて確率的な考え方を導入しましょう.すなわち作業時間が,ある分布に従う確率変数とみなす ということです.このアプローチにより,統計的な手法を用いて分析を行うことが可能になります.図表 5.5 作業時間の変化の結果
S
A
B
C
D
E
F
T
0[0,0,0] 4[0,5.7,1.7] 4[4,11.2,4.2] 5[0,5.2,0.2] 5.2[0,5.2,0] 5.5[5.2,11.2,0.5] 6[5.2,11.2,0] 0[11.2,11.2,0] case 2S
A
B
C
D
E
F
T
0[0,0,0] 8[0,8,0] 1[8,11.5,2.5] 3[0,5.5,2.5] 5.2[0,5.5,0.3] 3.5[8,11.5,0] 6[5.2,11.5,0.3] 0[11.5,11.5,0] case 3S
A
B
C
D
E
F
T
0[0,0,0] 4[0,5.2,1.2] 3[4,10.7,3.7] 3[0,5.2,2.2] 5.2[0,5.2,0] 5.5[5.2,10.7,0] 2[5.2,10.7,3.5] 0[10.7,10.7,0] case 45.2. PERTの例 131 今回は,分布として 2.9.6 節で紹介した三角分布を用います.三角分布は,最小値,最大値,最 頻値(最尤値)によって決まります.図表 5.6 における設定では,最小値と最大値の中間値を最頻 値とするので,結果的に平均値と最頻値が等しくなります.この設定では,平均作業時間がケース 1の場合の作業時間と等しいことに注意してください.作業時間の実現値は平均値を上回ったり下 回ったりするものの,プロジェクトの完了時刻は平均的にはケース1の場合で得た完了時刻と等し くなると期待してよいでしょうか? 図表 5.6 三角分布にしたがう作業時間(右は作業 F の分布) 作業 平均作業時間 最小値 最大値 A 6 4 8 B 4 3 5 C 6.2 5.2 7.2 D 2 1 3 E 4.5 3.5 5.5 F 4 2 6 0 2 4 6
5.2.3
シミュレーションの結果
シミュレーションによって何を知りたいかをあらかじめ挙げておきましょう. • [課題1]:プロジェクトの完了時刻がどのような分布になるか. • [課題2]:各作業がどの程度クリティカル・パスになるか. 作業時間が確率的に変動するならば,プロジェクト全体の完了時刻も同様です.この分布を解 析的に求めることができる場合もありますが,一般には困難であるため,計算機によって数値的に 求めざるを得ません. 計算といっても,原理は簡単です.前節では作業時間の変動について 4 つのケースをみました. これを,4つだけではなく,できるだけ沢山のケースについて調べるのです.その際,それぞれの ケースにおける作業時間は,与えられた分布に従うように値を決めます.得られた作業時間によっ て,プロジェクトの完了時刻を求め,それを記録しておきます.各作業がクリティカル・パスに 乗っているかどうかも,一つ一つのケースで時間分析を行い,クリティカル・パスを求めるだけで 確認できます.手作業では面倒なことも,計算機と適切なソフトウェアを用いればそれほどの手間 ではありません. 詳しくは計算機によるデモを見てもらうとして,結果の概略を記しておきます.ケースを発生 させた回数 (試行回数) を 10,000 回としました. プロジェクトの完了時刻については,次の通りです. 試行回数:10000 平均値:11.10 分散(標準偏差):0.38(0.62) 平均値が 11.10 となっていることに着目してください.平均値のみで計算した場合(ケース1)の ときは 10.7 でした.わずかな差に見えますが,統計的に有意な差です.理論的にも,作業時間が 変動する場合,プロジェクトの完了時刻の平均値は,作業時間をその平均値で計算した場合の完了 時刻より大きくなることを示すことができます (演習問題 5.1). 6つの作業がどの程度クリティカル・パスになるかについて,次の結果を得ました.作業 non CP CP 確率 A 6389回 3611回 36% B 10000回 0回 0% C 3610回 6390回 64% D 10000回 0回 0% E 2292回 7708回 77% F 7706 2294回 23% 今回の設定では,作業 B,D がクリティカル・パスに載ることはありません.作業 C と D がクリ ティカル・パスを構成することが相対的には多くなりますが,作業 A と F がクリティカル・パス にのる可能性も無視すべきではないでしょう. 演習問題5.1 図表5.7の左の図で示したようなプロジェクト・ネットワークがあるとする(S,Tはそれぞれ スタート,フィニッシュを表す).アクティビテイaとアクティビテイbの作業時間は確率的に 変動し,その分布は図表5.7の右の表の通りである.aとbの作業時間は独立な分布に従うもの とする. 1. アクティビテイaとbの作業時間の平均値を求め,その平均値に基いてプロジェクトの終 了時間を求めよ. 2. アクティビテイaとbの作業時間の同時分布に基づいて,プロジェクトの終了時間の分布 を求め,その平均値を求めよ. 3. 作業時間が任意の分布をする場合であっても,平均値に基づいたプロジェクトの終了時刻 と,プロジェクトの終了時刻の分布に基づく平均値では,必ず後者が前者より小さくはな らないことを示せ. 図表 5.7 プロジェクト・ネットワークと作業時間の分布 アクティビティa 作業時間の実現値 3 6 確率 1/3 2/3 アクティビティb 作業時間の実現値 1 7 確率 1/2 1/2
5.3
販売計画
新製品を開発して,市場で販売する計画を検討しましょう.まず確定的なモデルを考え,それ に不確実性を導入してシミュレーションで評価することにします. この計画では,設備投資により新製品の製造設備をつくり,売上によって得た利益で設備投資 を回収する予定です.計画期間を5期間とます.5.3. 販売計画 133
5.3.1
売上げと費用
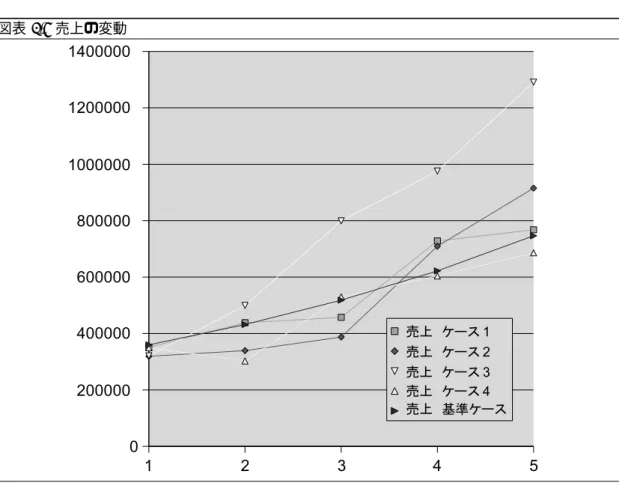
売上は,販売価格に販売数量をかければ得られます.販売価格は 600 円として,売上は毎期, 前期比20%増で成長すると仮定します.初年度の販売数量が 6000 個とすれば,計画期間中の売 り上げを求めることができます.費用を変動費用と固定費用にわけました.変動費用は,原材料費 に販売数量をかけたものとします.原材料費は一定で,製品 1 個当たり 300 円です.また,固定費 用も計画期間中に変動せず,100 万円とします.変動費と固定費をあわせて費用として,売上から 引くと(営業)利益が計算できます. 図表 5.8 売上と費用 販売数量は需要によって決まるので,不確実な数値とみなすのが自然です.平均的には前節で 見たような売り上げが実現するとしても,実際に実現する売上はもっと異なるものとなるでしょう. 図表 5.9 は,そのような不確実性を表現した例です.前節の設定を基準ケースとして,初年度の売 上およびその成長率が変動しています.固定費用についても同様で,毎期固定ではなく変動する場 合を想定することができます.5.3.2
総合収支
売上と費用がわかれば営業利益がわかります.しかし,それだけでは事業計画を評価すること はできません.設備投資のために利用した長期借入金の返済,税金などを考慮する必要があります.図表 5.9 売上の変動 この計画では,つぎのようなスキームとなっています. 設備投資額:800 万円 回収期間:5 期間 金利:2.5 % 税率:40 % 残存価値:10 % 借入金:600 万円 返済方法:元利均等返済 自己資本:350 万円 耐用年数:5 期間 残存率:10 % 償却方法:定額法 簡単に,収支の計算について説明します. • 設備投資をまかなうために,自己資本に加えて長期借入を行っています.この借入は利子を つけて返済しなければなりません.これは営業利益から支払うことになります. • 返済方法は,元利均等返済です.元金均等返済にした場合は,各期の返済額が異なります. • 最終的な収支を評価するために,計画期間(5 期間)が終了した後での設備の価値(残存価 値)を設備投資額の 10 %としました. • 利益に応じて税金の額が決まります.ただし,会計上,減価償却を考慮しなくてはなりません.
5.3. 販売計画 135
5.3.3
シミュレーション
以上の設定をスプレッド・シート上で表現しました.さらに,ソフトを利用して,この計画の 収支についてシミュレーションしてみます.
137
第
6
章 動的計画法
—
先読みと後知恵
時間軸に沿って状態が推移するときに,逐次的に行動を起こして,なるべく状態 を望ましい方向に持っていきたいとします.現在のある時点でとった行動が当面 の損得のみならず,継続して生起する将来の状態に影響を与えることによって長 期的な影響を持つことがあります.その場合,その時点での損得と将来の損得の 両方のバランスを取りながら現在の行動を決める必要があります. 現時点での損得は比較的評価しやすい一方,将来への影響の評価は簡単でありま せん.しかし,状態と行動の関係を,時間を後ろ向きに遡って評価することによ り,現時点と将来のバランスをとった決定をすることができます.6.1
クッキーの前売り販売
あなたのサークルでは,1000 枚のクッキーを大学祭で販売する予定です.売れ残りが心配なの で,この数年,前売り販売を導入してきました.これは,当日の販売価格 100 円よりも安い価格 90円で予約販売をするというものです.この数年の前売り枚数と当日の販売枚数の実績をみると, 次のような関係があることがわかりました. [当日の販売枚数] = 1.2× [前売り販売枚数] + 340 (6.1) 口コミの効果なのか,リピーターがいるためなのか,前売りの枚数が増えるとその分だけ当日の 売上も増加するようなのです.(6.1) の関係を所与とした場合,何枚のクッキーを予約販売すると トータルの売上が最大になるかを考えてみましょう. 前売りの販売価格は,当日の販売価格より 1 割安いので,そのことだけを考えるとあまり前売 りの枚数を多くしすぎるのは得策ではありません.しかし,一方で,前売り販売数が大きくなると 当日の売上も増加する関係があるので,この観点からは前売り枚数を増やすことには意味がありま す.前売り枚数の売上に対する,前者の直接的な効果と,後者の間接的な効果がバランスする点が 最適な予約販売枚数となるはずです. uを予約販売する枚数,前売りの売上額を x0,当日の売り上げを x1とおきましょう.前売り の販売価格は 90 円なので, x0= 90u (6.2) となります.(6.1) より,x1= 100(1.2u + 340)となるはずですが,当日販売できるクッキーの枚数 の上限があります.クッキーの総枚数は 1000 枚であるため,上限は 1000 − u です.したがって, 当日の売り上げは次のようになります. x1= 100 min{1.2u + 340, 1000 − u} (6.3)トータルの売り上げを最大にするに前売り枚数は,(6.2),(6.3) のもとで, max
0≤u≤1000(x0+ x1) (6.4)
を解くことで得られます. (6.2),(6.3) より,
x0+ x1= 90u + 100 min{1.2u + 340, 1000 − u} = 100 min{2.1u + 340, 1000 − 0.1u}
と変形できます.min{2.1u + 340, 1000 − 0.1u} を図示すると,図表 6.1 のようになります(太線で 表示).グラフは,u = 300 で最大になるので,売上を最大にする前売り枚数は 300 枚であること がわかります. 図表 6.1 min{2.1u + 340, 1000 − 0.1u} のグラフ 演習問題6.1 当日の販売枚数と前売り販売枚数の関係が [当日の販売枚数] = 1:2× [前売り販売枚数] + 120 であった場合,および [当日の販売枚数] = 0:8× [前売り販売枚数] + 340 であった場合について,トータルの売上を最大にする販売枚数をそれぞれ求めよ.
6.2. 投資と業績 139
6.2
投資と業績
前節では,当日前/当日の 2 期間にわたる問題でした.期間が増えた場合について考えてみま しょう.6.2.1
投資による企業の状態の変化
企業が今から 4 期間にわたって投資を行うことになっています.投資の効果は,投資を行う時 点,およびそのときの企業の状態—良い,普通,悪いのいずれか— の二つに依存して決まり,そ れは表 6.2 によって与えられます.この表によれば,0 期に普通の状態にあったときに,次の期に 良い状態となるためには 5 単位の投資が必要です.また,2 期に普通の状態にあったときに,次の 期に良い状態となるためには 7 単位の投資が必要です. 図表 6.2 状態の推移と投資額の関係 0,1期の投資 2,3期の投資 良い 普通 悪い 良い状態の時 3 2 0 普通の状態の時 5 2 1 悪い状態の時 8 3 1 良い 普通 悪い 良い状態の時 5 4 1 普通の状態の時 7 4 2 悪い状態の時 11 5 2 0期に普通の状態であった場合,4 期目に良い状態となるための最小の投資額は幾らか,を考 えましょう.この問題は状態の推移とそれに要する投資額をグラフで表すと分かりやすくなりま す(図表 6.3).端点が各時点の状態を,枝が状態の推移を,枝の数字が投資額をそれぞれ表して います. 図表 6.3 投資額と状態の推移の関係 (G:良い,N:普通,B:悪い)G
G
G
G
N
N
N
N
B
B
B
B
t=0
t=1
t=2
t=3
G
N
B
t=4
3
2
0
3
2
0
5
2
1
5
2
1
8
3
1
8
3
1
5
4
1
7
4
2
11
5
2
11
5
2
7
4
2
5
4
1
4期間の投資を一度に考えるとはたいへんですが,ある期に次の期のことだけを考える 1 期間 の問題は簡単です.そこで,まず,4 期目に良い状態になるという目標を実現するには,まず 3 期目にどの投資を行うべきかを考えることにしましょう.次に,遡って 2 期目,1 期目の投資を考え, 最後に 0 期における投資を考えることによって,4 期間の問題を解くことができるはずです.それ をまとめたのが,図表 6.4 です.端点の上の枠内の数値が,その時点・状態から出発して 4 期目に 良い状態になるための最小の投資額を示しています.0 期に普通の状態であった場合,4 期目に良 い状態となるための最小の費用は 14 です.この場合,各期の投資額は,1–1–5–7 となります. 図表 6.4 各時点・各状態のおける目標達成のための最小投資額
G
G
G
G
N
N
N
N
B
B
B
B
t=0
t=1
t=2
t=3
G
N
B
t=4
3
2
0
3
2
0
5
2
1
5
2
1
8
3
1
8
3
1
5
4
1
7
4
2
11
5
2
11
5
2
7
4
2
5
4
1
5
7
11
10
11
12
12
13
13
13
14
14
演習問題6.2 状態の推移と投資額の関係が,図表6.2から図表6.5に変わったとする.この場合,第0期に普 通の状態から出発して,第4期に良い状態となるための最小の費用を求めなさい. 図表 6.5 状態の推移と投資額の関係 2 0,1期の投資 2,3期の投資 良い 普通 悪い 良い状態の時 4 1 0 普通の状態の時 5 3 1 悪い状態の時 8 5 1 良い 普通 悪い 良い状態の時 3 2 1 普通の状態の時 8 4 2 悪い状態の時 12 5 16.2.2
投資による収益
前節の問題を少し変えて,投資によって得られる収益を考慮しましょう.収益は業績に応じて 変化するものとし,業績は投資額に依存するとします.投資と業績の関係は,図表 6.2 のままであ6.3. 動的計画法の解法 141 図表 6.6 業績と収益 0,1,2期の収益 3,4期の収益 良い状態の時 3 5 普通の状態の時 2.1 2.5 悪い状態の時 0 -1 るとし,状態によって決まる収益は表 6.6 で与えられます.5 期間の収支(=収益─投資)の合計 を最大にするには,どのような投資を行えばよいでしょうか. この問題も,やはり最後の第 4 期目から遡って考えることで,最適な投資計画を求めることが できます.最適な投資計画と収益の関係は図表 6.7 で与えられます.端点の上の枠内の数値が,そ の時点・状態から出発して最適な投資をした場合の収支の総計を示しています. 図表 6.7 最適な投資のもとでの収支
G
G
G
G
N
N
N
N
B
B
B
B
t=0
t=1
t=2
t=3
G
N
B
t=4
3
2
0
3
2
0
5
2
1
5
2
1
8
3
1
8
3
1
5
4
1
7
4
2
11
5
2
11
5
2
7
4
2
5
4
1
5
1
-3.5
3
0.1
-4
3
0.2
-2.9
3
0.3
-2.8
5
2.5
-1
演習問題6.3 状態の推移と投資額の関係が,図表6.2から図表6.5に変わったとする.この場合,第0期に普 通の状態から出発して,5期間の収支が最大になるのはどのような投資を行った場合か.6.3
動的計画法の解法
以下では,離散時間・確定的な動的計画問題について考察します.不確実性を含む場合や連続 時間の場合は,別途専門書を参照してください.6.3.1
問題の記述
• 状態が離散時間で観測され,以下の方程式を満たす. xt+1= ft(xt, ut), t= 0, 1, . . . , N − 1 (6.5) ただし, t :時点を表すインデックス xt:時点 t における状態変数 ut:時点 t における制御変数 である. 状態 xtは,状態空間 Stに属する.制御変数 utは,その時点の状態 xtによって定まる制約 領域 Ut(xt)を持つ. • 加法的な費用関数を持つ. 0から N − 1 までの各時点 t で,状態 xt,制御 utに応じた費用 gt(xt, ut)がかかる,最終時 点 N においては,状態 xNのみに依存する費用 gN(xN)がかかる.全体の費用は,加法的に g0(x0, u0) + g1(x1, u1) +· · · + gN−1(xN−1, uN−1) + gN(xN) (6.6) と表される. • 許容可能な方策を持つ. 方策 (制御規則)π とは,t = 0, 1, . . . , N − 1 における制御 utを決める規則であり, π={µ0, µ1, . . . , µN−1} (6.7) として与えられる.µt()は,その時の状態 xtに対して制御 utを決めるという意味で関数で あり ut= µt(xt), t= 0, 1, . . . , N − 1 とかける.すべての t について,任意の xt∈ Stに関して µt(xt)∈ Ut(xt)ならばその方策 は許容可能 (addmissible) であるという. 以上をまとめると,問題は次のように記述される. Jπ∗(x0) = min π∈ΠJπ(x0) (6.8) Jπ(x0) = gN(xN) + N−1∑ t=1 gt(xt, ut) (6.9) ここで,Π はすべての許容可能な方策の集合であり,x0は初期状態を表す.6.3. 動的計画法の解法 143
6.3.2
最適化原理と動的計画法のアルゴリズム
問題 (6.8) の最適な方策 π∗={µ∗0, µ∗1, . . . , µ∗N−1} が与えられているとする.ここで,部分問題 min µi,µi+1,...,µN−1 gN(xN) + N−1∑ t=i gt(xt, ut) (6.10) を考える.部分問題 (6.10) の最適な方策は,{µ∗ i, µ∗i+1, . . . , µ∗N−1} である. この性質を動的計画問題の最適化原理 (principle of optimality) と呼びます.最適化原理を利用 して,動的計画法のアルゴリズムを構築することできます.具体的には,以下のような再帰方程式 を定義します. JN(xN) = gN(xN) (6.11) Jt(xt) = min ut∈Ut(xt) { gt(xt, ut) + Jt+1(ft(xt, ut)) } (6.12) (6.12)を t が N − 1 から 0 まで順番に解き,u∗t= µ∗t(xt)を求めると,π∗={µ∗0, µ∗1, . . . , µ∗N−1} が 最適な方策となるのです. 実際に,6.2.2 節の問題に適用してみることにしましょう.この場合,N = 4 です.また,状態 は,t = 0, 1, . . . , 4 にたいして xt= G, 状態が良いとき N, 状態が普通のとき B, 状態が悪いとき と表すことにします.制御変数 utは,時点 t で行う投資額を表します.また,各時点の収支を表 す関数 gt(xt, ut)は gt(xt, ut) = [時点 t で状態 xtにいるときの収益 ] − ut, t= 0, 1, . . . , 3 となります.時点 4 では投資は行わないので,g4(x4)はその状態における収益のみを表します. (i) t= 4において, g4(G) = 5 g4(N) = 2.5 g4(B) = −1 となるので,(6.11) より J4(G) = 5 J4(N) = 2.5 J4(B) = −1 となります. (ii) t= 3: (6.12)より, J3(x3) = min ut {g 3(x3, u3) + J4(f3(x3, u3))} と表されます.x3= Gの場合で考えましょう. t= 3では,u3(投資額) は,5 か 4 か 1 のいずれかなので, g3(G, 5) = 5 − 5 = 0 g3(G, 4) = 5 − 4 = 1 g3(G, 1) = 5 − 1 = 4 です.推移を表す f3(x3, u3)については, f3(G, 5) = G f3(G, 4) = N f3(G, 1) = B となります.以上から, g3(G, 5) + J4(f3(G, 5)) = g3(G, 5) + J4(G) = 0 + 5 = 5 g3(G, 4) + J4(f3(G, 4)) = g3(G, 4) + J4(N) = 1 + 2.5 = 3.5 g3(G, 1) + J4(f3(G, 1)) = g3(G, 1) + J4(B) = 4 − 1 = 3 が得られます.したがって, J3(G) = max u3∈{5,4,1} {g3(G, u3) + J4(f3(G, u3))} = 5 となり,最適な方策は µ3(G) = 5となります. 同様に,x3= Nの場合, g3(N, 7) + J4(f3(N, 7)) = g3(N, 7) + J4(G) = 2.5 − 7 + 5 = 0.5 g3(N, 4) + J4(f3(N, 4)) = g3(N, 4) + J4(N) = 2.5 − 4 + 2.5 = 1 g3(N, 2) + J4(f3(N, 2)) = g3(N, 2) + J4(B) = 2.5 − 2 − 1 = −0.5 となるので,µ3(N) = 4で,J3(N) = 1です. x3= Bの場合, g3(B, 11) + J4(f3(B, 11)) = g3(B, 11) + J4(G) = −1 − 11 + 5 = −7 g3(B, 5) + J4(f3(B, 5)) = g3(B, 5) + J4(N) = −1 − 5 + 2.5 = −3.5 g3(B, 2) + J4(f3(B, 2)) = g3(B, 2) + J4(B) = −1 − 2 − 1 = −4 となるので,µ3(B) = 5で,J3(B) = −3.5です. (iii) t= 2: 再度,(6.12) を用いて,J2(x2)を計算していきます. x2= Gの場合は, g2(G, 5) + J3(f2(G, 5)) = g2(G, 5) + J3(G) = 3 − 5 + 5 = 3 g2(G, 4) + J3(f2(G, 4)) = g2(G, 4) + J3(N) = 3 − 4 + 1 = 0 g2(G, 1) + J3(f2(G, 1)) = g2(G, 1) + J3(B) = 3 − 1 − 3.5 = −1.5 となるので,µ2(G) = 5で,J2(G) = 3です.
6.4. 参考:最適消費問題 145 同様の計算により, µ2(N) = 7 J2(N) = 0.1 µ2(B) = 5 J2(B) = −4 となります. (iv) t= 1: 計算結果のみ示します. µ1(G) = 3 J1(G) = 3 µ1(N) = 2 J1(N) = 0.2 µ1(B) = 3 J1(B) = −2.9 (v) t= 0: 計算結果のみ示します. µ0(G) = 3 J0(G) = 3 µ0(N) = 2 J0(N) = 0.3 µ0(B) = 3 J0(B) = −2.8 J0(x0)が得られた時点で,すべての問題が解けたことになります.上記の結果が,図表 6.6 と 同じ結果になっていることを確認してください. 演習問題6.4 上記の手続きにしたがって計算を行うことで,J1(x1)とJ0(x0)の数値が正しいことを確認せよ.
6.4
参考:最適消費問題
前節までの問題は,状態も制御変数が離散的な値しか取らなかった.どちらも連続的に変化し うる場合についても考えてみましょう. 初期資産額 x0から出発して N 期間投資を行うものとします.各期で得られた収益の一部を消 費し,残りを再び投資にまわします.k 期の期首の資産価値 xkから Ckを消費し,Ikを投資しま す.投資の対象は n 種類あり,資産 j の k 期末の収益率は Rjkです.期首には, xk= Ik+ Ck, k= 0, . . . , N − 1 Ik= n ∑ j=1 ujk が成り立っていて,投資額は期末には, n ∑ j=1 (1 + Rjk)ujk= Ik+ n ∑ j=1 Rjkujkとなります.以上をまとめると, xk+1= xk− Ck+ n ∑ j=1 Rjkujk (6.13) n ∑ j=1 ujk= xk− Ck (6.14) が得られます.消費から得られる効用を ϕ(Ck),また最終的な資産価値から得られる効用を ϕ(xN) とすると,最適な消費を求める問題は max E { γNϕ(xN) + ∑N−1 k=1 γkϕ(Ck) } s.t. xk+1= xk− Ck+ ∑n j=1Rjkujk, k= 1, . . . , N − 1 ∑n j=1ujk= xk− Ck, k= 1, . . . , N − 1 として定式化されます.ただし,γkは適当な割引係数です. 以下では,簡単化のため,投資対象の資産は 1 種類のみとしましょう.問題は, max E { γNϕ(xN) + ∑N−1 k=1 γkϕ(Ck) } s.t. xk+1= xk− Ck+ Rkuk, k= 1, . . . , N − 1 uk= xk− Ck, k= 1, . . . , N − 1 と表されます.ukを消去して, max E { γNϕ(xN) + ∑N−1 k=1 γkϕ(Ck) } s.t. xk+1= (1 + Rk)(xk− Ck), k= 1, . . . , N − 1 を得ます.また,効用関数 ϕ(·) を ϕ(Ck) = 1 αC α k, α < 1 とおき,γk= γkとします. 1. つぎのように関数を定義する. JN(xN) = E[γN 1 αx α N] Jk(xk) = max Ck E{γk1 αC α k + Jk+1((1 + Rk)(xk− Ck))}, k = 0, . . . , N − 1 2. k= N − 1のとき JN−1(xN−1) = max CN−1 E{γN−11 αC α N−1+ JN((1 + RN−1)(xN−1− CN−1))} (6.15) となる.右辺は, C∗N−1= xN−1 1+ (γAN−1) 1 1−α = BN−1xN−1, (AN−1≡ E[(1 + RN−1)α]) のとき最大となり, JN−1(xN−1) ={BαN−1+ γAN−1(1 − BN−1)α}γN−1 1 αx α N−1= DN−1γN−1 1 αx α N−1 となる.
6.4. 参考:最適消費問題 147 3. k= N − 2のとき JN−2(xN−2) = max CN−2 E{γN−21 αC α N−2+ JN−1((1 + RN−2)(xN−2− CN−2))} (6.16) (6.16)は (6.15) と構造が全く同じなので,k = N − 1 と同様に JN−2(CN−2)を得ることがで きる.(6.16) の右辺の最大化は, C∗N−2= xN−2 1+ (γDN−1AN−2) 1 1−α = BN−2xN−2, (AN−2≡ E[(1 + RN−2)α]) で達成され, JN−2(xN−2) ={BαN−2+ γDN−1AN−2(1 − BN−2)α}γN−2 1 αx α N−2= DN−2γN−2 1 αx α N−2 となる. 4. 一般の k のとき xkのもとでの最適な消費は, C∗k = xk 1+ (γDk+1Ak) 1 1−α = Bkxk, (Ak≡ E[(1 + Rk)α]) であり, Jk(xk) ={Bαk + γDk+1Ak(1 − Bk)α}γk 1 αx α k = Dkγk 1 αx α k を得る. C∗kの式より,最適な消費は常にその時点の保有資産の一定の比率になることがわかります.こ れは別の効用関数でも同様の結果を得ることができます.例えば,冪乗型効用関数のかわりに,対 数型を用いると,(6.15) は, JN−1(xN−1) = max CN−1 E{γN−1log CN−1+ γNlog((1 + RN−1)(xN−1− CN−1))} (6.17) となり,右辺は, C∗N−1= 1 1+ γxN−1 のとき最大となります.
![図表 5.5 作業時間の変化の結果 S AB C DEF T0[0,0,0]4[0,5.7,1.7]4[4,11.2,4.2]5[0,5.2,0.2] 5.2[0,5.2,0] 5.5[5.2,11.2,0.5]6[5.2,11.2,0] 0[11.2,11.2,0]case 2 S AB C DEF T0[0,0,0]8[0,8,0]1[8,11.5,2.5]3[0,5.5,2.5] 5.2[0,5.5,0.3] 3.5[8,11.5,0] 6[5.2,11.5,0.3] 0[11.5,11.5,0]ca](https://thumb-ap.123doks.com/thumbv2/123deta/6036280.583738/4.892.157.795.237.1043/図表作業時間変化結果SABCDEFT881811525355252.webp)