2
運動の法則
2.1
速度と加速度
第1週で、x 軸上(例えばエアートラック上)にある物体の運動は、その 位置 x、速度 vx、加速度 axで表すことができることを学んだ。これからの 実験の内容をよりよく理解するために、基本的な力学の物理量を簡単に整理 しておこう。 2.1.1 速度 位置 x は、エアートラック上で適当な位置に原点 (x = 0) を取り、その原 点からの距離 x[m] で指定することができる。また、エアートラック上(ト ラックに沿って x 軸をとる)を運動する物体の速度 vxは、1秒間 (1s) あた りに物体が進む距離という意味を持つ物理量である: vx [m/s] = 1 秒間における位置の変化 [m] 1 s . (1) ここで、速度を表す変数として速度 velocity の頭文字 v を使って、v と表す。 添え字のxは x 成分を示している1。(単位は SI 単位系2で、[m/s] である。) ただし、物体が常に一定の速度で運動する(等速直線運動の)場合は (1) 式で 速度を決めても差し支えないが、物体の速度が刻一刻と変化する場合は、よ り短い時間間隔 ∆t[s] で速度を決める必要がある。(1) 式の意味をそのままに 速度を決めるには、∆t 秒間で移動した距離をその移動に要した時間 ∆t で割 ればよい: ¯ vx [m/s] = ∆t 秒間における位置の変化 [m] ∆t . (2) これを、平均の速度という3。少し具体的に考えてみよう。例えば、次の表 1 のように時刻 t1に位置 x1にあった物体が、時刻 t2に位置 xxへ位置が変化 (変位)したとしよう4。このとき、平均の速度は (2) 式で分母は ∆t = t 2− t1 であり、分子は ∆x = x2− x1であるので、 ¯ vx [m/s] = ∆x ∆t = x2− x1 t2− t1 (3) で表される。さらに、時間の間隔 ∆t = t2− t1を非常に小さく、数学的には 無限小に、つまり2回目の測定時刻 t2を1回目の測定時刻 t1の直後に近づ 1物理量の表記は、斜字体(イタリック体)を利用する。t, x, v など。一方、単位の表記には、 立体(ローマン体)で表記することに注意せよ。[s], [m], [m/s] など。単位は、文字式の後の表 記は [ ] 内に、数値の後は [ ] は付けずに標記すうる。例えば、L[m], T [s], v[m/s] , 4.1 m, 2.3 s, 5.2 m/s など。 2国際単位系とも呼ばれる。 3平均の速度は、¯をつけて、¯v と表すこととする。 4ここで、x 1とは、時刻 t1での物体の位置である。物体の位置 x は一般に時間 t と共に変化 していく。これを物体の位置 x は時間 t の関数であるととらえて、x(t) と表す。従って、x1, x2 は x(t1), x(t2) と表しても良い。表 1: 直線上を運動する物体の位置と時間 時刻 位置 時間変化 変位 平均速度 速度 t [s] x(t) [m] ∆t [s] ∆x [m] v¯x vx[m/s] t1 x1= x(t1) t2− t1 x2− x1 x2− x1 t2− t1 dx dt t2 x2= x(t2) (t2→ t1の極限) ける t1→ t2 の極限を考えよう5。このとき(3)式の分子と分母はともに小 さくなるが、それらの比は一定の値に近づく。この操作を微分と言い、その 一定となる比の値 vx [m/s] = lim ∆t→0 ∆x ∆t = dx dt (4) を物体の(瞬間の)速度と呼ぶ。 2.1.2 加速度 次に、物体の速度変化を表す物理量である加速度 a を考えよう。加速度は 1秒間あたりの速度変化である。もし、物体の速度が一定の割合で変化し続 ける場合は、 a [m/s2] = 1秒間のおける速度の変化 [m/s] 1 s (5) となる。なお、加速度の文字式は acceleration の頭文字 a を使って a と表す ことが多い。(SI 単位系で)加速度の単位は、[m/s2] である。この速度の変 化が時間とともに変化するような、より一般の場合には平均の速度を定義し た時と同じように短い時間間隔 ∆t を使って、 ¯ ax[m/s2] = ∆t 秒間における速度の変化 [m/s] ∆t (6) と定義しよう。これを ∆t 秒間の平均の加速度と呼ぶ。実際に実験では、二 つの異なる時刻 t1と t2の間隔 ∆t = t2− t1に、速度が vx1 から vx2に変化 するときの度変化を ∆vx= vx2− vx1として、平均の加速度を ¯ ax[m/s2] = vx2− vx1 t2− t1 = ∆vx ∆t (7) と定義する。ここで、(速度の場合に考えたように、再び微分の考えを使う と)時間間隔 ∆t = t2− t1を無限小にする極限を考えて、(瞬間の)加速度を 5この極限では ∆t が小さくなるとともに、∆x も小さくなっていくことに注意しよう。
速度の時間1階微分(位置 x の時間に関する2階微分6) ax[m/s2] = lim ∆t→0 ∆vx ∆t = dvx dt = d2x dt2 (8) で定義する。表 2 に速度と加速度のまとめを示した7。 表 2: 直線上を運動する物体の位置と時間 時刻 位置 速度 平均加速度 加速度 t [s] x [m] vx ¯ax[m/s2] ax [m/s2] t1 x1= x(t1) vx1= dx(t) dt t=t1 vx2− vx1 t2− t1 dvx dt (= d2x dt2) t2 x2= x(t2) vx2= dx(t) dt t=t2
2.2
運動の法則
高校では、力とは物体を変形させたり、物体の運動の状態を変えたりする 原因となるなるもの、と学んだ8。ここでは物体の変形は考えないこととし、 運動の状態の変化とその原因としての力の関係を、定性的・定量的に確認す ることを、この節の目標としよう。2.1 節でみたように、運動の様子を表現す るために必要となる基本的な物理量は、位置 x、速度 v、加速度 a であった。 ならば、運動状態の「変化」を捉える為には、どの物理量の変化に着目すべ きであろうか? 2.2.1 運動の状態 どの力学的物理量が変化したとき「運動の状態」が変化したととらえ、そ の原因となる力が加わったと考えるべきだろうか? この問に答えるために、 先ず、力が働いてない ということを定義し、その上で「力」を定義しよう。 ニュートンの第1法則: 物体に作用する力がなければ(働いている すべての力の和、合力がゼロならば)、その物体の 速度は変化しない 6 d dt( dx dt) を d2x dt2 と表す。 7注目する物体は直線上を運動するとは限らないので、一般の(x-y-z の3次元空間内の)運 動の場合は、それぞれベクトルで ⃗x = ( x, y, z), ⃗v = (vx, vy, vz), ⃗a = (ax, ay, az) で表 されることに注意しよう。 8例えば、國友正和他, 「物理学基礎」, 数研出版, 平成 23 年検定済, p.38. などを参照せよ。これは、ニュートン (Newton, Sir Isaac: 1643-1727) の運動の第1法則(い わゆる慣性の法則)と呼ばれる。ここで慣性とは、物体がその速度を保つ性 質のことであり、ガリレイ (Galilei, Galileo:1564-1642) によってその基本的 な考え9が提案された10。すなわち、物体がとり得る様々な運動の形態のうち で等速直線運動がもっとも基本的なものと考え、ニュートンはその仮説を運 動の法則を定量的に表すための足掛かりとした。 エアートラック上で静止している滑走体を指で軽く押して運動させる状況 を考えよう。指が触れる前まで静止していた滑走体の速度は、指が触れて滑 走体に力が加わっている間はその速度が変化している。すなわち、指から滑 走体に力が加わっているのである。また、指から離れて滑走体を滑りはじめ ると(空気抵抗や滑走体とトラックの間の摩擦が無視できれば)滑走体に水 平成分の力は働かない11。従って、滑走体の水平方向の速度成分に変化は生 じない12。 指から離れてエアートラック上を運動する物体は、時間とともに、位置 x は変化する。しかし、速度 v が時間とともに変化しなければ、力は働いてな い(もしくは、力が打ち消し合っている)ということを主張するのが、ニュー トンの運動の第1法則だ。また、速度 v が時間とともに変化するときは、加 速度 a がゼロでないことに注意しよう。((8) 式を参照)速度の変化を「運動 の変化」と捉えると、このとき必ず加速度が生じることになる。 問い: 水平なエアートラック上の滑走体を、図 1 のように、一定の大きさの 力で水平に引き続ける。このとき、滑走体の運動はどうなるだろうか? 1 ⃝ 引いている間、どんどん速くなる(加速する)。 2 ⃝ 引き始めた直後から一定の速さになる。 3 ⃝ 引いている途中から一定の速さになる。
2.3
質量と加速度の関係
同じ力を加えても、物体によって生じる速度変化、すなわち加速度は異な る。このことは、日常の中でもよく経験したり、目にしたりする事実だ。スー パーで、品物を満載し質量が大きくなったカートは動かしにくいし、またレ 9例えば、原島 鮮, 「力学(三訂版)」, 裳華房 (1985) p.19. などを参照せよ。 10ガリレイは実際に実験することなく、現象を理論にもとづいて思考的に追及する思考実験に より、物体に慣性という性質があることを提唱した。 11力は互いに接触することで物体から物体にはたらく力と、重力や電磁気力のように、重力場 や電場、磁場というような場から物体にはたらく力がある。この例では、水平方向に重力や電磁 気力などの力の作用はないので、何も接触していない物体に力は作用しない。すなわち、指を離 れた滑走体には水平方向の力は働いていない。 12滑走体には、鉛直方向には重力が作用しているはずだ。しかし、鉛直方向に加速度は生じて ない。これはなぜか?図 1: エアートラック上の滑走体を一定の大きさの力で引き続ける ジで止めにくい。物体には慣性があるが、質量の大きなカートはそれだけ運 動状態を変えにくいので慣性が大きい、と言える。質量は慣性の大小を表し ている量である。 エアートラックに静止している、おもりを載せていない 100 g の滑走体と、 20 g のおもりを載せた 120g の滑走体にそれぞれ同じ力を加えたとき、二つ の滑走体の加速度にはどのような関係があるだろうか?実験室で確かめるこ とができるように、120 g の滑走体がもつ加速度の大きさは、100 g の滑走体 のもつ加速度に比べて小さい。 同じ力を加えても生じる加速度が異なる理由は、このように運動する物体 の質量の違いにある。我々は第 1 週の「速度・加速度」の実験で確認したよ うに、摩擦を(ある程度)無視できるエアートラック上の滑走体の運動の記 録から加速度を求めることができた。ならば、予め定められた質量 1 kg を 基準として13、この 1 kg の物体に大きさ 1 m/s2の加速度を生じさせる力の 大きさを 1 N (ニュートン) と決めることができる。このとき、慣性の大 きな(質量の大きな)物体ほど、同一の力を加えたとき、運動が変化しにく い(生じる加速度が小さい)ので、 同じ力を加えて生じる加速度の大きさは、質量に反比例する を認めれば、これをもとに(慣性)質量を決めることができる。例えば、摩擦 や空気抵抗の無い状況下で、ある物体に大きさ 1 N の力を加えたところ、加 速度が 2.0 m/s2となれば、その物体の質量は 0.5kg と決めることができる。 また、他のある物体に大きさ 1 N の力を加えたところ、加速度が 0.5 m/s2 となれば、その物体の質量は 2 kg と決めることができる。 13質量 1 kg の基準がどのように定められているか、調べてみよ
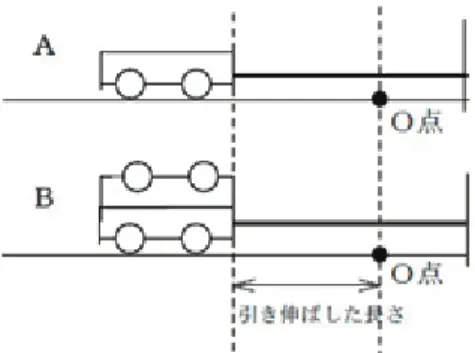
図 2: どちらの台車が O 点を先に通過するだろうか? 問い: 図 2 のように、同じゴムひもに A(台車1台)、B(台車2台)を取 り付け、同じ長さだけ引き伸ばして同時にスタートさせた。図の O 点を早く 通過するのは、A,B どちらの台車だろうか?(ただし、床と台車の間の摩擦 は無視できるものとする。 1 ⃝ A の方が早く O 点を通過する 2 ⃝ B の方が早く O 点を通過する 3 ⃝ A, B 同時に O 点を通過する
2.4
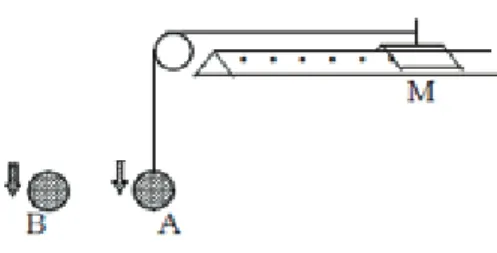
ニュートンの運動の第2法則
ニュートンの第一法則で力が作用していない場合の運動が示された。次に、 力が作用した場合の法則を調べよう。これまで説明してきたように、力は、 物体の運動を観測する(加速度を測定する)ことにより定義された。しかし、 身近なばねやゴムひものような、フックの法則に従う弾性体の性質を利用す ると、より直観的に理解できるであろう。ここでフックの法則とは、ばねや ゴムひもの伸びが2倍3倍になれば、ゴムやばねの弾性体から及ぼされる力 の大きさも2倍、3倍になるという実験的、経験的事実である。これを認め れば、比較的簡単な実験によって次のことがわかる。すなわち、ニュートン の第1法則で力が作用してない場合の運動を先ず定義したうえで、 • 力 ⃗F の作用により速度 ⃗v が変化すること(加速度 ⃗a が生じること) — 物体に取り付けたゴムを自然長から2倍、3 倍の長さに伸ばして物 体を引く場合、その加速度が2倍、3倍になる。 — • 生じる加速度 ⃗a は質量 m に反比例すること — 物体に取り付けたゴムを自然長から同じ長さだけ伸ばして物体を引 く場合、物体の質量を2倍、3倍とすれば、その加速度が 1/2 倍、1/3 倍になる。 —図 3: 自由落下する B に比べて A はどのように落下するだろうか? を定量的な法則としてまとめることができる14。これを一つの式で表すと、 ⃗a = ⃗F /m となるだろう。これが、ニュートンの運動の第2法則と呼ばれるも のであり、以下の (9) 式は、運動方程式15と広く呼ばれている。 ニュートンの第2法則: 物体に作用する力(複数の力が作用して いる場合はそれらの合力) ⃗F は、物体の質量 m と物体の加速度 の積に等しい: ⃗ F = m⃗a (9) 問い: 図 3 のように、摩擦が無視できるエアートラック上の滑走体 M とお もり A を糸で結んで滑車に通し、M を手で支えて静止させている。いま、お もり A と同じ質量のおもり B を A と同じ高さで支え、滑走体 A とおもり B の支えを同時に取りのぞいた。自由落下する B と比較して、A はどのように 落下するだろうか? 1 ⃝ A は B と同じように速度変化しながら(下向きに加速しつつ)ともに 同じように落下する。 2 ⃝ B に比べて A の速度変化は小さく、B よりもゆっくりと落下する。 3 ⃝ B に比べて A の速度変化は大きく、B よりも速く落下する。 また、どうしてそのように考えたか、理由を説明しなさい。 14ここでは、より一般的に力と加速度をそれぞれ ⃗F と ⃗a とベクトルの表式で表した。ここま での説明では、エアートラック上などのように、1次元の運動であったので、x 成分だけに着目 してきたが、一般の3次元空間 (x, y, z 空間) 内では、力や加速度はそれぞれ x, y, z 成分をもつ ベクトルとして表記されることが多い。すなわち、 ⃗F = (Fx, Fy, Fz), ⃗a = (ax, ay, az) である。 15運動方程式 F = ma は、12 = 3× 4 という数学的なイコールとは、意味が少し異なること に注意してほしい。運動方程式のイコールで分けられる右辺と左辺は、F は運動の【原因】とな る力と、(質量 m を比例係数として、)力の作用の【結果】としての加速度 a がイコールで結ば れているのである。もちろん、右辺と左辺は数値的にも等しいが、それは力の大きさ1 N の定義 のおかげである。どちらかと言うと、【原因】⇒【結果】の意味合いが強いイコールだ。その意 味で、物理の運動方程式は因果律と呼ばれる。原因と結果を結びつけるルール(律)だからだ。
2.5
一定の大きさの力を物体に作用させる場合
エアートラック上の滑走体のように、エアートラックと滑走体の間の摩擦 力が無視できるような状況で、滑走体に一定の大きさの力 F0を水平方向に 加える場合を考えよう。このとき、他に力は水平方向に作用しないので、質 量 m の滑走体にたいする運動方程式(水平方向)は、 F0= max (10) となる。従って、滑走体の加速度 axは、ax= F0/m(一定の値)となること がわかる。このとき、滑走体の位置や速度は、時間とともに、どのように変 化するだろうか。物理の問題としては、時刻 t = 0 の初期位置 x = x0と初速 度 vx= v0の初期条件が与えられれば、この問題を解く(任意の時間の滑走 体の位置や速度を計算する)ことができる。 加速度は速度の時間微分であったことを思い出すと、 dvx dt = ax= F0 m (11) という滑走体の速度 vxと加速度 ax= F0/m の関係が、どんな時間でも(任 意の時間に対して)成立している。上の (11) のような式は、速度の微分(左 辺)を含む方程式であり、一般に微分方程式と呼ばれる。この式を解くこと は、それほど難しいことではない。なぜならば、時間で微分したら一定の数 axになる16、そういう時間の関数としての速度 vx(t) を見つければ良いから だ。高校の数学で学んだ、整数べきの関数の微分を思い出そう:f (x) = xn を x で微分すれば、 df dx = d dxx n= nxn−1 である。また、x0= 1 であることを思い出すと、(11) 式は、 vx= axt + C (12) となることがわかる17。ここで、C は時間に依らない定数である。と呼ばれる もので、初期条件から決まる定数である。試しに、(12) を時間 t で微分して みれば、これが (11) 式の解となっていることがわかるだろう18。この解(12) 16ここで取り扱っている問題は、a xは定数であり、その値が F0/m である。以降、一般の等 加速度運動の場合を念頭に、F0/m の代わりに、axのまま表記する。 17この (12) 式は、より直接的に導出することができる。(11) 式のように、もっとも簡単な微 分方程式は積分により解くことができる。(11) 式の両辺を (初期時刻 t = 0 から時刻 t まで) 時 間で積分することで、 ∫ t 0 dvx dt dt = ∫ t 0 axdt となる。左辺は微分積分の定理から直ちに、vx(t)− v0であり、右辺は axt である。これより (12) 式を得る。 18時間によらない定数 C を時間 t で微分してもゼロである。すなわち、d dtC = 0.式は、任意の時間で正しく成立している必要がある。よって、t = 0 で速度が v0を満足しなければならない19。これより、vx(0) = ax· 0 + C = v0 となる 必要があるので、C = v0と決まる。最終的に、微分方程式(物理の言葉なら 運動方程式)の解は、 vx= ax t + v0 (13) と求めることができる20。同じように、速度 v x= ax+ v0が位置 x の時間微 分で与えられたことを思い出すと、 dx dt = axt + v0 (14) という微分方程式を得る。速度の場合と全く同じように、この式も解くこと ができる21。初期条件 t = 0 で初期位置 x(0) = x 0を使って、その解は、 x(t) = 1 2axt 2+ v 0t + x0 (15) と求めることがわかる。運動方程式の解 (13) 式, (15) 式から分かるように、 等加速度運動の場合、位置 x は時間 t の 2 次関数、速度 v は時間の 1 次関数 として変化することがわかる。
2.6
理解を深める為の演習問題
2-1 次の式は粒子の位置 x(t) を表している22。x はメートルで、t は秒で測り、 t > 0 とする。 (a) 速度が一定の粒子は、次の (1)∼(4) のうち、どれか? (b) 時刻が t = 1s のとき、粒子の速度が x の負の向きであるのは、次の (1) ∼(4) のうち、どれか? (1) x = 3(m/s) t− 2(m) (2) x =−4(m/s2) t2− 3(m) (3) x = 2(m/s2) t2− 6(m/s) t − 20(m) (4) x =−2(m) 19そういう初期条件が課せられていた。見落としている場合は、前頁に記述を確認せよ。 20高校では、等加速度運動の「公式」として学習したのではなかろうか。ここで、みたように、 これは、ニュートンの運動の法則を解くことによって導くことができる。 21この微分方程式も、(11)式の場合と同じように解いてみよ。 22これらの表式は、やや奇妙に見えるかも知れない。しかし、この様に表されることは起こり 得る。例えば、運動する物体をデジタルビデオカメラで撮影し、時間をコマ送りしながら、物体 の位置を読み取る。それらの位置を表計算ソフト(エクセル)などで読み込み、データ点を適当 な関数(この場合は時間の冪関数)でフィットした場合などである。図 4: (D. ハリディ, R. レスニック, J. ウォーカー, 野崎光昭 訳, 「物理学の 基礎」[1] 力学, 培風館 (2002), p 13, 例題2−2 より転載) エレベータ は、時間が t = 1 s から t = 3s と、t = 8 s から t = 9 s までは、グラフ(図 2-2(c) からわかるように、それぞれ正と負の加速度の等加速度運動をしてい る(問題文にもあるように、鉛直上向きが正の向き)。この区間の x-t グラフ (図 2-6(a)) をみてみると、この区間は、それぞれ下と上に凸の 2 次曲線(時 間に関する2次関数)になっている。一方、t = 3 s から t = 8 s の区間で、 x− t グラフは傾きが一定の直線になっており、エレベーターの速度が一定で あることが読み取れる。実際、v− t グラフ(図 2-6(b)) をみると、速度が一 定となっていることが確認できる。 2-2 粒子の x 軸上の位置が次式で与えられたとする。(x はメートル、t は秒で測 られており、t > 0 とする。) x = 4− 27t + t3 (a) 粒子の速度 v(t) と、加速度 a(t) を求めなさい。 (b) v = 0 となる速度を求めなさい。 2-3 水平面に置かれた物体に、水平右向きに 5 N の力を、また水平左向きに 2N を同時に加えた。(ただし、2つの力の向きは一直線上であるとする。)この とき、次の問に答えよ。
(a) このブロックの加速度の大きさと向きを答えよ。
(b) 動き始めた物体に力を加えて、その後等速直線運動となるようにするた めには、どの向きにどれだけの力を加えればよいか?
3
第3週 力学的エネルギーの保存
高校で学んだ「物理基礎」において、「エネルギー」がどのように取り扱 われていたか思い出してみよう。高校の教科書によると、物理では、『ある物 体が他の物体に仕事をする能力を持っているとき、その物体は「エネルギー を持っている」という』と書かれている。 そこで、「仕事」に関して調べて みると、『(ある物体が他の)物体に力を加えて動かしたとき、力は物体に対 して仕事をしたという』と書かれている。従って、エネルギーを持つ状態と は、物体に力を作用させて動かすことができる状態となる。このことを、実 際の実験と結び付けて定量的に理解するために、もう少し掘り下げて考えて みよう。3.1
仕事
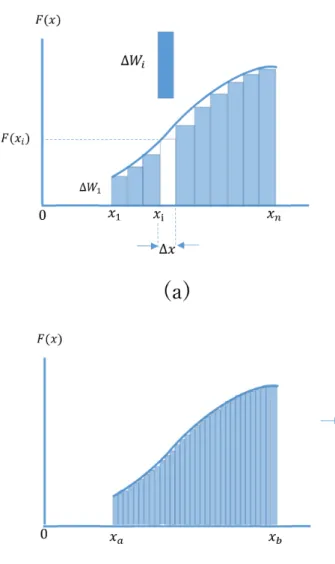
力 Fxを加えて動かす、すわち物体の速度が変化しつつ物体の位置が ∆x だ け変位したとき、力は(物体に)仕事をしたという。この定義に基づくと、 (力が加わり変位が生じることで物体に与えられたエネルギーにあたる)仕 事23は、物体に作用する力 F xと物体の変位 ∆x の両方に比例する。従って、 もっとも単純な「仕事」に対する表式は、 ∆W = Fx∆x (16) となるだろう24。なお、(SI 単位系で)仕事の単位は、(16) 式からもわかる ように、[N·m] である。後に明らかになるように、仕事はエネルギーと同じ 次元の物理量である。エネルギーの単位はジュール [J] が広く用いられるの で、仕事を [J] で表してもよい。 (16) 式で注目すべきこととして、その右辺は注目する物体に加わった力と 物体の変位の積が、(16) 式左辺の物体へ移動したエネルギーと等しいと読み 取ることができる、というところにある。ただし、(16) 式は、物体が力を受 けつつ ∆x の変位をする間は、力 Fxが一定で変わらない場合に成立する。例 えば、図 5(a) のように、物体に作用する力 Fxが物体の変位とともに変化す る場合には、それがほぼ一定と見なせるような小さな変位、例えば x1から x1+ ∆x の変位で力 Fxがする仕事 (図 5(a) の1番左の長方形の面積) は、 ∆W1= Fx(x1)∆x (x1から x + ∆x までの仕事) 23仕事(Work) の頭文字を取って W と表そう 24ここでは、もっとも簡単な場合の一例として、物体に力を加える方向も、物体が動く方向も、 ともに x 方向としている。より一般的には、力は大きさと向きを持つベクトル ⃗F = (Fx, Fy, Fz) として与えられ、変位もベクトル ∆⃗r = (∆x, ∆y, ∆z) で与えられる。この場合、仕事は、力と 変位のベクトル同士の積(内積と呼ばれる)になり、 W = ⃗F· d⃗x = Fx∆x + Fy∆y + Fx∆z で与えられる。とできるだろう。ここで、x1から x1+∆x までは力が一定と見なせるとした ので、Fx(x1)≈ Fx(x1+ ∆x) である。そこで、この変位で物体に作用した力 は、位置 x1で作用した力 Fx(x1) で代表させている。まったく同様に x1+ ∆x から x + 2∆x (これを、x2と表そう; すなわち、xn = x1+ (n− 1) × ∆x で ある25) までは、その変位の間に作用した力を F x(x + ∆x) で代表させて ∆W2= Fx(x2)∆x (x1+ ∆x から x + 2∆x までの仕事) となる (図 5(a) の2番左の長方形の面積)。これらの、小さな変位 ∆x の仕事 ∆W1, ∆W2,· · · を加えていくことで、最終的に求めたい終状態の位置 (x1+ n∆x) までの変位に伴う仕事を求めることができる: ∆W1 = Fx(x1)∆x +∆W2 = +Fx(x2)∆x +∆W3 = +Fx(x3)∆x · · · = · · · +∆Wn = +Fx(xn)∆x, すなわち、 W = n ∑ i=1 ∆Wi= n ∑ i=1 Fx(xi)∆x (17) である。次に、微小な区間 ∆x を図 5(b) のように小さくしていこう。図から わかるように、∆x を小さくすると、次第に(17)式の和は、徐々に曲線の下 の部分の面積に近づいていく。そしてここで、この ∆x を無限小とする極限 を考えよう。無限小の変位は dx で表す (∆x→ dx)。このとき、一つ一つの 変位からの仕事への寄与も無限小になり( ∆Wn → dW )、(17) 式の n は、 無限大に近づいていくことに注意しよう。無限に小さな寄与 dW を無限に足 し合わせる、この様な数学的な操作を積分と呼び、例えば、物体が力 Fxを 受けつつ位置 xaから xbまで変位した場合、力がした仕事は W = ∫ xb xa Fx(x)dx (18) と表す。 25一般に定義する場合の数学記号は ‘≡’ である。例えば、この例の場合は x n≡ x1+(n−1) ∆x と表す。
図 5: 式(17)から式(18)にいたる概念図: (a) は、物体の位置の変化とと もに、変化する力の様子を表している。区間を有限ないくつかの区間にわけ、 変位に伴う仕事を、∆Wiの和として近似している。各区間で物体に作用する 力の大きさは、区間の左端の xiで作用する力の大きさ F (xi) がその区間内で は一定に作用すると見なす近似が取られている。(∆x が小さくになるにつれ て、この近似は良くなることに注意しよう。)(b) は、∆x が (a) より小さな 値の場合の様子。そして、この ∆x を無限小とした極限が連続極限と呼ばれ る。ことのき、力が物体にする仕事 W は、曲線 F (x) と x = xa, x = xb及 び x 軸で囲まれる領域の面積と等しい。
一方、物体に作用する力と仕事の関係を変位を通してではなく、時間変化 で表わした方が都合が良い場合もある。そこで、(16) 式を次のように変形し よう26: ∆W = Fx ∆x ∆t ∆t = Fxv¯x ∆t. (19) ここで ¯vx は平均の速度であり、時間間隔 ∆t を(無限小の dt まで)小さ くしていくと、平均の速度 ¯vx は(瞬間の)速度 v に近づくので (19) 式を dW = Fxvxdt、または両辺 dt で“ 割り算 ”(数学的には微分)して P = dW dt = Fxvx. (20) と書くことができる。この (20) 式は、仕事率 と呼ばれる物理量である27。(仕 事率の単位は [J/s] であり、通常 [W] ワットで表わされる。)仕事が物体 へ移動するエネルギーであると説明したが、この仕事率は単位時間(1秒間) あたりに物体に作用する力を通して物体に移動するエネルギーという意味を 持つ。例えば、時刻 t = 0 から時刻 t まで力を加え続けた場合、物体へ移動 した全エネルギー、すなわち物体に力がした仕事 W は、(20) 式を積分する ことで求めることができる: W = ∫ dW = ∫ t 0 Fxvxdt. (21) この (21) 式は、(9) 式の運動方程式 Fx= mdvdtx を使うと28 ∫ t 0 Fxvxdt = m ∫ t 0 dvx dt vx dt = m ∫ t 0 d dt [ 1 2v 2 x ] dt が得られ、上式の最後の積分はすぐに実行できて、 m ∫ t 0 d dt [ 1 2v 2 x ] dt = m [ 1 2v 2 x ]t t=0 = 1 2mv 2 x− 1 2mv 2 x0 となる。ここで、vxは時刻 t での速度、vx0は時刻 t = 0 での速度を表して いる。これまでの結果をまとめると、 W = 1 2mv 2 x− 1 2mv 2 x0. (22) となることがわかる。この (22) 式に現れる 1 2mv 2 xは、時刻 t における運動エ ネルギー と呼ばれる物理量で、1 2mv 2 x0を同様に時刻 t = 0 の運動エネルギー と見なすと、(22) 式の右辺は時刻 t = 0 から時刻 t までの運動エネルギーの 変化をあらわしている。このように (22) 式は、力 Fxによってなされた仕事 W が物体に移動したエネルギー(運動エネルギーの変化)と等しいことを示 している。この(22)式は、仕事と運動エネルギーの定理と呼ばれる物理法 則を表す式である。 26この式変形は、∆t ∆t = 1 が掛けられているだけなので、(2番目の)等式の成立に影響がな いことに注意しよう。 27仕事率は、英語表記 Power の頭文字をとり、 P が用いられることが多い。 28この式の最後の等号は、[ ] の部分を実際に時間で微分してみれば成立することが確認でき る。
3.2
力学的エネルギーの保存
実際に具体的な力を考えて、これまでの仕事とエネルギーに関する考察を さらに進めよう。ここでは、我々の身の回りでもっとも身近な力のひとつで ある重力を例にとって、力による仕事と運動エネルギーの変化を具体的に調 べてみることにしよう。重力は、地球と質量 m の物体の間に働く万有引力を 起因とする力で、地表付近における重力加速度の大きさ g とするとき29、大 きさ mg の鉛直下向きの力である。 いま、x 軸を鉛直上向きにとり、地表を x = 0(原点)として座標を設定 する30。重力による仕事だけを考えたいので、運動中の空気抵抗などは考え ない。物体を高さ x1の位置から初速 vx1で鉛直方向に投げ出して 31、ある点 x2まで運動したときに、重力が物体にした仕事を (18) 式を利用して求めよ う。この場合、(18) 式の Fxは、−mg となる (鉛直上向きを変位の正の向き に取っていて重力の向きは鉛直下向きであることに注意せよ32)。このとき、 物体がどのような運動をしても(位置 x に依らずに)、重力は大きさも向きも 変わらない33ので、(18) 式の−mg は積分の「外」に出すことができて、積 分は終点 x2と始点 x1だけで決まることがわかる。 W =−mg ∫ x2 x1 dx =−mg (x2− x1). (23) 一方、x2の位置における物体の速度を vx2と表すことにすると、仕事と運動 エネルギーの定理 (22) 式より、 −mg (x2− x1) = 1 2mv 2 x2− 1 2mv 2 x1 を得る。この式を整理すると、 1 2mv 2 x1+ mgx1 = 1 2mv 2 x2+ mgx2 (24) が成立することがわかる。この式は、任意の時間において34運動エネルギー35 K =1 2mv 2 x (25) 29標準重力加速度の大きさ (緯度 45 °、海面 ) は、g =9.80665 m/s2である。重力加速度は、 地球の緯度だけではなく、局所的な地球内部の密度にも影響を受けるので、場所によってその大 きさが異なることが知られている。例えば、羽田(東京大田区)の値は、g =9.79760 m/s2で ある。 30もちろん、鉛直上向きを z 軸として、これまでの数式で xとしてきた部分をzと読み替え ても、もちろん構わない。 31座標軸は鉛直上向きを正の向きに定義しているので v x0> 0 ならば、鉛直投げ上げ、vx0< 0 ならば、鉛直投げ下ろしとなる 32鉛直下向きを変位の正の向きに取る場合は dx は正、mg も正となるが、積分の上底と下底 の大小関係が反転して結果的に (23) 式と同じ結果になることに注意しよう。従って、(23) 式は、 x1と x2の大小関係に依らず、いつでも正しい結果を与えてくれる 33もちろん、物体の質量 m が変わらなければ、である。 34x 2は任意に (どんな値でも勝手に) 決めた点であることを思い出そう。 35Kinetic energy(運動エネルギー) の頭文字を K をとって、運動エネルギーを文字式 K で 表すことが多い。と、基準の位置(x = 0)から鉛直方向への変位 x(すなわち、基準からの高 さ)だけで決まる重力の位置エネルギー(重力ポテンシャルエネルギー)と 呼ばれる量 U (x) = mgx =−1 × [ −mg ∫ x 0 dx ] (26) の和が一定に保たれることを意味している。ここで、この重力ポテンシャル エネルギーは、質量 m の物体を x = 0 から高さ x まで変位させるときに、重 力が物体にする仕事 W の符号を反転させた量 (−W ) となっていることに注 意しよう36。なぜ、ポテンシャルエネルギーにはマイナス符号が現れるのかを 理解する為に、地表 (x = 0) に静止している物体を、高さ x = h まで持ち上 げて静止させる場合を考えよう。このとき、物体には重力の他に、持ち上げ るための外力を加えられているが、(x = 0 での「静止」した状態から、x = h までの「静止」した状態までの変化なので)物体の運動エネルギーに変化は なく、仕事と運動エネルギーの定理から、重力と外力のする仕事の和はゼロ となることに注意しよう。従って、このとき物体に作用した外力(物体を持ち 上げた力)がした仕事は、重力がする仕事にマイナスを掛けた量に等しいこ とになる。物体と地球の系37には、この外力がした仕事が、位置エネルギー として「蓄えられた」と見なすこともできるだろう。これを、我々は重力ポ テンシャルエネルギーと呼ぶのである。 一般に、運動エネルギーとポテンシャルエネルギー(位置エネルギー)の 和は力学的エネルギーと呼ばれ、重力や電磁気力など保存力と呼ばれる力の ポテンシャルエネルギーと運動エネルギーの和は一定に保たれ、物体の運動 を解析する際に重要な役割を果たすことが多い。より一般的な保存力 F に対 して、その力のポテンシャルエネルギーは、位置 x = x0がポテンシャルエネ ルギーの基準 U (x0) = 0 としてエネルギーは U (x) =−∆W = − ∫ x x0 F (x) dx (27) で定義される。 36((23) 式で、x 1= x, x2= x とした場合が、この場合の重力がする仕事。これにマイナス を掛けた量が (26) 式である。) 37地球と物体のように、互いに力やエネルギーのやり取りし合うような2つ以上の物体(地球 も物体!)を「系」と呼ぶ(地球-物体-系 ”などと呼ぶ)。ここでは、重力は地球と物体の間に はたらく力であり、重力ポテンシャルエネルギーは地球と物体の位置関係で決まる。重力ポテン シャルエネルギー、(重力の)位置エネルギーは、「物体」に蓄えられるというようり、「物体と 地球の系」に蓄えられると言った方が正確な表現である。
問い: 図 6 の (1),(2),(3) のそれぞれの A の位置から質量 m の小球、おも ちゃのジェットコースター、振り子を静かに放した。このとき、B 点(A 点 より高さが h だけ下の点)を通過するそれぞれの物体の速さについて述べて いるもののうち、適当なものはどれか?ただし、それぞれの物体にはたらく 空気抵抗や摩擦は無視できるのもとする。 1 ⃝ (1) の小球がもっとも速い 2 ⃝ (2) のジェットコースターがもっとも速い 3 ⃝ (3) の振り子がもっとも速い 4 ⃝ どれも同じ速さである。 5 ⃝ これだけではわからない。 図 6: B 点を通過する速さがもっとも大きな物体はどれか? 問い: 図 7 のように、Q 点から高さ h の斜面上にビー玉を静かに置いたと ころ、ビー玉は曲面に沿って運動したあと Q 点から飛び出し、P 点に置かれ た箱に命中した。次に、ビー玉を高さ 2h の位置から静かに放して同じように 箱にビー玉を命中させたい。このとき、箱は OP 間の距離の何倍の位置に置 く必要があるか? 図 7: ビー玉を置く高さを 2 倍にして箱に命中させるためは、箱はどこに置 けばよいか?
3.3
理解を深める為の演習問題
3-1 質量 m[kg] の物体にはたらく重力がちょうど 1 N であった。この物体の質量 m は何 kg か? 3-2 (a) 質量 60 kg の人が秒速 4 m の速足で歩いている。この人の運動エネルギー は何 J か? (b) 1.5 L の水のペットボトルが床から 1 m のテーブルの上に載せてある。 このペットボトルの重力ポテンシャルエネルギーは何 J か。 (c) 床から 1 m の高さに静止していた 1.5 L の水が入っているペットボトル が鉛直に落下した。床に落下するときのペットボトルの速さを求めよ。 3-3 粒子が x 軸に沿って移動する。もし、粒子の速度が (a)−3 m/s から −2 m/s に、(b) −2 m/s から +2 m/s に 変化したら、運 動エネルギーは増加するか、減少するか、または変化しないか? (c) それぞれの場合、粒子になされた仕事は正か、負か、ゼロか?4
第4週 運動量の保存
物体の運動の勢い(激しさ)を表す量の一つとして、「質量×速度」という 量を考え、それを運動量と呼ぶことを高校で学んだ。さらに、着目している いくつかの物体の集まり(物体の「系」と呼ぶ)を考えるとき38、その系の 外部から作用する力(「外力」と呼ぶ)がない場合は、系をなす物体の運動量 の和は変化しない(運動量の保存)。これらのことを、簡単な実験で調べてみ ることにしよう。4.1
運動量の変化と力積
先ずは、粒子が1つだけの場合を考えてみよう。ニュートンの運動の第2 法則として、2.4 節で力 ⃗F の作用と速度の変化 ⃗v に関係があることを学んだ。 従って、注目している物体の質量39 m と速度の積で定義される運動量40 ⃗ p = m⃗v (28) は力が作用すると変化し、力が作用しなければ(もしくは、いくつかの力が 作用していても、それらの合力がゼロであれば)変化しない。このことは、 (28) 式を時間で微分することで(数式的には)より明確になるだろう。 d⃗p dt = m d⃗v dt = ⃗F (29) 上の (29) 式で現れる微分は、無限小の短い時間 dt に、運動量が(やはり無 限小の大きさの変化である)d⃗p だけ変化する場合の「比」であると解釈する ことも可能だ。ここで、運動量が変化する時間が無限小でなくとも十分短い 時間、例えば、時刻 t から時刻 t + ∆t の間に作用する力が大きく変化しない 場合は、その間の運動量の変化 ∆⃗p = ⃗p(t + ∆t)− ⃗p(t) と ∆t の比は、 ∆⃗p ∆t = m ∆⃗v ∆t = ⃗F (t) (30) として良い41。すると、(30) 式の両辺に ∆t を掛けることで ∆⃗p = ⃗F (t)∆t (31) 38それぞれの物体を大きさを無視できる質点と捉えるとき、これらの系を特に質点系というこ とがある。 39質量の大きさは時間とともに変化しないと仮定する。 40運動量は p という文字で表されることがおおい。速度は、「大きさ」と「向き」を持つ量で あるので、ベクトル ⃗v として表されたことを思い出そう。この速度に、大きさだけの量(スカ ラーという)である質量 m を掛けた運動量も、ベクトル量になる。従って p の上部に⃗ を付け て ⃗p で表している。 41ここで、 ⃗F は、時間が ∆t の間でほぼ変化しないと考えたことに注意しよう。これは、 ⃗ F (t) = ⃗F (t + ∆t) が成立してるので (30) 式の右辺の ⃗F は、特に時刻 t での力 ⃗F (t) であらわ している。が得られる。しかし、力が例えば、時刻 t = t1から時刻 t = t2まで、時々 刻々と変化していく場合はどうすればよいだろうか。この場合は、力がほぼ 一定と見なせる十分に短い時間間隔 ∆t を考えて、その間の運動量の変化を 計算して足し合わせることで、t1から t2までの全運動量の変化を見積もれる と考える。すなわち42、時刻 t 2と t1の間を n 等分する ∆t = (t2− t1)/n の とき43、 ∆⃗p(t1+ ∆t) = F (t⃗ 1)∆t ∆⃗p(t1+ 2∆t) = F (t⃗ 1+ ∆t)∆t · · · ∆⃗p(t1+ n∆t) = F (t⃗ 1+ n∆t)∆t の左辺と右辺のそれぞれの和を取ればよい。改めて時間の間隔 ∆t を無限に 小さくとる場合のこれらの和を、右辺と左辺をそれぞれ、運動量と力に関す る時間積分とみなすことができ、次のように表される: ∫ t2 t1 d⃗p = ∫ t2 t1 ⃗ F (t) dt ( ≡ ⃗J ) (32) この (32) 式の左辺は積分の計算を実行することができて、これは時刻 t1か ら t2の間の運動量の変化を表していることを示している: ∫ t2 t1 d⃗p = [ ⃗ p(t) ]t2 t1 = ⃗p(t2)− ⃗p(t1). (33) また、右辺は、力積と呼ばれる物理量である。(ここで、最後の≡ は、”定義す る”を示す記号で、力積という(ベクトル量の) 物理量を ⃗J で今後表すことを 意味している。)このように、物体に与えられた ((33) 式の左辺の) 力積 ⃗J は、 ((33) 式の右辺の)運動量の変化と等しい ことがわかる。
4.2
質点系の運動量とその保存
ここでは、2つ以上の物体からなる物体系を考えよう。例えば、2つの物 体の衝突現象などを考える際には、これらの2つ物体を1つの系として取り 扱うとよい。もちろん、それぞれの物体(ここでは、質量 m1の物体1と質 量 m2の物体2)に対しては、4.1 節で学んだニュートンの運動の法則は成り 立っている。従って、時刻 t と t + ∆t の間の時間 ∆t に、物体1に力 ⃗F1が 作用し物体2に力 ⃗F2が作用すると、それぞれの運動量の変化は ∆⃗p1= ⃗F1(t)∆t , ∆⃗p2= ⃗F2(t)∆t 42時刻が t = t 1から t = t1+ ∆t の間、力は時刻 t = t1の瞬間の力 F (t1) の値を使ってい ることに注意しよう。他の時間も同様である。 43t 2= t1+ n∆t であるである。ここで、衝突現象のような場合、力 ⃗F1(t) と ⃗F2(t) の間には、どの ような関係があるだろうか。重要なことは、力 ⃗F1(t) は物体1に作用する力 であるが、これは物体2から及ぼされた力であるということである。同様に、 ⃗ F2(t) は、物体2に作用する力で、これは物体1から及ぼされた力であるとい うことである。この事実を意識して、改めて ∆⃗p1= ⃗F12(t)∆t (34) ∆⃗p2= ⃗F21(t)∆t (35) と表し直そう。すなわち、⃗F12は、物体 2 から物体 1 に作用した力を、⃗F21は、 物体 1 から物体 2 に作用した力を意味している。また、このとき、⃗F12と ⃗F21 は互いに作用・反作用の関係にあると言い、これらの力は (どの時刻 t でも!) ⃗ F12(t) =− ⃗F21(t) (36) が成り立つことが知られている。実際、このことは、運動に関するニュート ンの第3法則として、次のようにまとめられる。 ニュートンの第 3 法則: 2つの物体が相互作用するとき(力を及 ぼし合うとき)、それぞれの物体が他方の物体に及ぼす力の大き さは等しく、力の向きは反対である。 従って、(34) 式と (35) の両辺をそれぞれを加えると、時刻 t によらずに ∆p1(t) + ∆p2(t) = 0. (37) となる。任意の時刻 t で (37) 式が成り立つので、時間 ∆t を無限小として考 え、時刻 t1から t2まで、(32) 式を導いたときと同じように考えると、二つ の物体の系に対しては、 ∫ t2 t1 d⃗p1+ ∫ t2 t1 d⃗p2= ∫ t2 t1 ( ⃗ F12(t) + ⃗F21(t) ) = 0 (38) が得られる。左辺を積分して整理すると、 ⃗ p1(t2) + ⃗p2(t2) = ⃗p1(t1) + ⃗p2(t1) (39) となる事がわかる。これは、物体1の運動量と物体2の運動量の和は、時刻 に関係なく一定に保たれることになる。このことを、二つの物体の運動量が 保存するという。
問い: 図 8 のように、台車 A と台車 B に輪ゴムをかけて、手で左右にひい てから両方の手を台車から同時に放した。台車 A と B には粘着テープが張っ てあり、衝突後両者は合体する。合体後の台車の運動量は次のうちのどれに なると予想されるか。 1 ⃝ 合体後、台車は右へ動く 2 ⃝ 合体後、台車は左へ動く 3 ⃝ 合体後、台車は静止する 図 8: 2 つの台車は衝突後どの様に運動するか 問い: 摩擦が無視できる床の上に置かれた質量 1.0 kg の台車 A と質量 2.0 kg の台車 B の間にばねを押し込み、台車 A と B を同時に放す。このとき、 A と B のそれぞれぞの台車が進んでいく方向に板を立て、2 台の台車が同時 にそれぞれの板と衝突させるようにしたい。このためには、静止している A と B の位置から、板を何対何となるような位置に板を置けばよいか。 1 ⃝ 1:1 2 ⃝ 1:2 3 ⃝ 2:1 図 9: 2 つの台車は衝突後どの様に運動するか
![表 1: 直線上を運動する物体の位置と時間 時刻 位置 時間変化 変位 平均速度 速度 t [s] x(t) [m] ∆t [s] ∆x [m] v ¯ x v x [m/s] t 1 x 1 = x(t 1 ) t 2 − t 1 x 2 − x 1 x 2 − x 1 t 2 − t 1 dxdt t 2 x 2 = x(t 2 ) (t 2 → t 1 の極限) ける t 1 → t 2 の極限を考えよう 5 。このとき(3)式の分子と分母はともに小 さくなるが、それらの比は一定の値に近づく。この操](https://thumb-ap.123doks.com/thumbv2/123deta/6361030.631989/2.892.218.675.212.353/∆¯−=極限ける考えようともにさくなるそれら近づく.webp)
![図 4: (D. ハリディ, R. レスニック, J. ウォーカー, 野崎光昭 訳, 「物理学の 基礎」[1] 力学, 培風館 (2002), p 13, 例題2−2 より転載) エレベータ は、時間が t = 1 s から t = 3s と、t = 8 s から t = 9 s までは、グラフ(図 2-2(c) からわかるように、それぞれ正と負の加速度の等加速度運動をしてい る(問題文にもあるように、鉛直上向きが正の向き)。この区間の x-t グラフ (図 2-6(a)) をみてみると、この区間は、それ](https://thumb-ap.123doks.com/thumbv2/123deta/6361030.631989/10.892.217.665.208.523/ハリディレスニックウォーカーエレベータグラフわかるそれぞれ.webp)