1
行列の作成と解放
1.1
行、列数が決まっている場合
行列は C においては 2 次元配列を用いて実現される。行数、列数が既知の場合は普通に ソース 1 double a[行数][列数]; により定義可能である。問題 1
3x3行列に 0 から 1 までの乱数をセットして 3x3 行列の形で表示するプログラムを作成せよ。 (表示例) 0.240 0.143 0.339 0.191 0.341 0.477 0.412 0.003 0.9211.2
列数が未定の場合
行数は分かっているが列数が未定の場合は malloc() を用いてメモリを確保する必要がある。はじめに ソース 2 double *a[行数];と「double 型のポインタの 1 次元配列」をスタック領域から確保した後に、malloc() で確保した「double 型の値を入れ る 1 次元配列」から各列の先頭アドレスを代入する。具体的には次のようにする。なお malloc() したら free() を忘れな いこと。 ソース 3 #include <stdio.h> #include <string.h> #include <stdlib.h> #define ROWS 3 #define COLS 3 int main() {
double *a[ ROWS ];
// メモリ確保
a[ 0 ] = ( double* )malloc( sizeof(double) * ROWS * COLS ); for( int i = 1; i < ROWS; ++i ) a[ i ] = a[ 0 ] + COLS * i;
// メモリ解放 free( a[ 0 ] );
return 0; }
問題 2
ソース 3 のメモリ確保部分について説明せよ1.3
行数、列数がともに未定の場合
行数、列数がともに未定の場合は、はじめにポインタのポインタ型を ソース 4 double **a; と定義して「double 型のポインタの 1 次元配列」を malloc() で確保する。これを「行列の先頭アドレス」と呼ぶことに する。あとは前節と全く同様に「double 型の値を入れる 1 次元配列」を malloc() で確保して各列の先頭アドレスを a[i] に代入していく。逆にメモリを解放する場合は「double 型の値を入れる 1 次元配列」を free() してから「double 型のポ インタの 1 次元配列」を free() する。つまり malloc() と free() はともに 2 回行う必要がある。今後は特に言及が無い限 り行列として行数、列数がともに未定の場合を扱うことにする。問題 3
行数、列数がともに未定の場合に行列の作成と解放を行うプログラムを作成せよ2
2
次元行列構造体
行数 (rows)、列数 (cols) の 2 次元行列を次の構造体で定義する。この MATRIX 構造体を使って関数間で行列のデー タをやりとりできる。 ソース 5 struct MATRIX { double** dat; // 2次元配列 int rows; // 行数 int cols; // 列数 }; 実際に使用する場合は次のようにする。ここで make mat() は次節で作成する行列作成関数である。 ソース 6 MATRIX A; A = make_mat( 10, 10 ); A.dat[0][0] = 1;
3
行列演算関数
以下に示す行列演算用の関数を作成する。なお行列演算に失敗した場合はエラーメッセージを表示し 、exit(1); を用い て強制終了するようにせよ。
1. 行数 (rows)、列数 (cols) の行列の作成を行う関数 MATRIX make mat( int rows, int cols ); 2. 行列のメモリ解放を行う関数 void free mat( MATRIX A );
3. 行列の中身表示を行う関数 void print mat( MATRIX A );
4. 行列の中身のコピー (A → B ) を行う関数 (B のメモリは予め確保しておく。コピーには memmove() 関数を使う こと) void copy mat( MATRIX A, MATRIX B );
5. 行列の中身の部分コピー (A[ r from ∼ r to ][ c from ∼ c to ] → B ) を行う関数 ( B のメモリは予め確保してお く ) void copy submat( MATRIX A, MATRIX B, int r from, int r to, int c from, int c to );
6. 転置行列 (AT→ B ) を求める関数 ( B のメモリは予め確保しておく ) void t mat( MATRIX A, MATRIX B );
7. 行列和 (A±B → C ) を求める関数 ( C のメモリは予め確保しておく ) void plus mat( MATRIX A, MATRIX B,
MATRIX C );及び minus mat( MATRIX A, MATRIX B, MATRIX C );
8. 行列積 (A*B → C ) を求める関数 ( C のメモリは予め確保しておく ) void prod mat( MATRIX A, MATRIX B, MATRIX C );
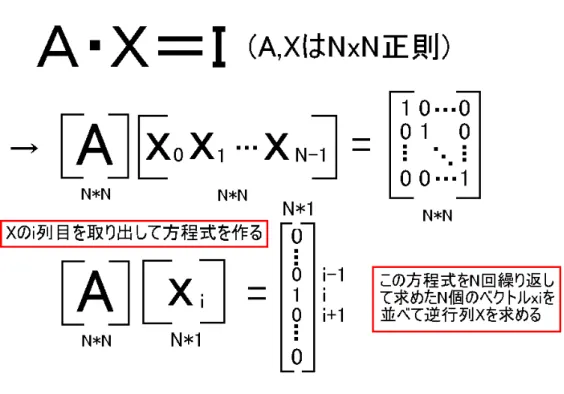
9. N次正方行列の逆行列 ( A−1 → B ) を求める関数 ( B のメモリは予め確保しておく。付録 A の線形連立方程式ラ イブラリを利用すること) void inverse mat( MATRIX A, MATRIX B );
図 1: 逆行列の求め方
問題 4
以上の関数群を作成し 、各自 main 関数を作成し 、テストして正常動作することを確認せよ。参考としてテス ト用 main 関数の作成例を付録 B に示す。4
csv
ファイルの読み書き
csvファイル ( comma separated value : カンマ区切り値 ) はテーブルデータをテキスト形式で表現するファイル形式 であり、表計算ソフトなどで広く使用されている。テーブルの各行は 1 行のテキストで表され 、各行の列 (フィールド と 呼ぶ) は数値、もしくは文字列で表され 、各フィールド の間はカンマ (,) で区切られる。例えば 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 という行列を csv ファイルで表すと 1.0, 2.0, 3.0 4.0, 5.0, 6.0 7.0, 8.0, 9.0 となる。
問題 5
行列の内容を csv ファイルに書き出す void write csv( char* filename, MATRIX A ); を前節で作成した関数 群に追加せよ。なお、書き込みに失敗した場合はエラーメッセージを出して exit(1); で終了すること。問題 6
関数群に csv ファイルから行列に値を読み込む void read csv( char* filename, MATRIX A ); を追加せよ。な お、読み込みに失敗した場合はエラーメッセージを出し 、exit(1); で終了せよ。また今回は問題を簡単にするために行数 と列数は既知であるとし 、MATRIX A は先に make mat() で作成しておくことにする。アルゴ リズムの流れは以下の通 りとなる。 1. fopen()でファイルを開く 2. fgets()で 1 行分のデータを読む 3. strtok()でカンマ毎に文字列を区切る 4. atof()で数値に変換する 5. 2∼4 を繰り返す 6. fclose()でファイルを閉じる 参考として strtok() の使用例を以下に示す。なお今回は問題を簡単にするために strtok() を使用したが、実際には様々な 理由から strtok() を使用してはいけない。詳しくはヘルプを見よ。 ソース 7 char buf[ 1024 ]; strcpy( buf, "1.0, 2.0, 3.0" ); char *p; char *q = buf; for(;;){ p = strtok( q, "," ); if( !p ) break; q = NULL;double val = atof( p );
fprintf( stdout, "%lf ", val );
}
問題 7
csvファイルを読み込み、値を適当に加工してから csv ファイルに出力するプログラムを作成し 、任意の表計 算ソフトとデータをやりとり出来ることを確認せよ付録
A
線形連立方程式
MATRIX make_mat( int rows, int cols ); void free_mat( MATRIX A );
// LU 分解 //
// src -> LU // dst = LU //
void lu_decomp( double** src, double** dst, int* pivot, int rows, int cols ) {
// src -> dst に内容をコピー for( int r = 0; r < rows; ++r ){
for( int c = 0; c < cols; ++c ){ dst[ r ][ c ] = src[ r ][ c ]; }
}
for( int r =0; r < rows; ++r ) pivot[ r ] = r;
int max_loop;
if( rows > cols ) max_loop = rows; else max_loop = cols;
for( int loop = 0; loop < max_loop; ++loop ){
// pivot計算
double maxval = dst[ pivot[ loop ] ][ loop ]; int maxrow = loop;
for( int r = loop + 1 ; r < rows; ++r ){ double tmpval = dst[ pivot[ r ] ][ loop ]; if( tmpval > maxval ){
maxval = tmpval; maxrow = r; }
}
int tmprow = pivot[ loop ]; pivot[ loop ] = pivot[ maxrow ]; pivot[ maxrow ] = tmprow;
// L 成分計算
// loop列の各行を左上の値で割りながらコピー for( int r = loop + 1 ; r < rows; ++r )
dst[ pivot[ r ] ][ loop ] /= dst[ pivot[ loop ] ][ loop ];
// 残差行列を計算
for( int r = loop + 1; r < rows; ++r ){ for( int c = loop + 1; c < cols; ++c ){
dst[ pivot[ r ] ][ c ] -= dst[ pivot[ r ] ][ loop ] * dst[ pivot[ loop ] ][ c ]; }
} } // // 線形連立方程式 Ax = y // // A[ N ][ N ] : N次正方行列 ( 入力データ ) // y[ N ] : 目的変数 ( 入力データ、長さ N のベクトル ) // x[ N ] : 説明変数 ( 出力データ、長さ N のベクトル ) //
void linear_equation( MATRIX A, double* x, double* y ) {
MATRIX LU; int N; int *pivot; double *z;
if( A.cols != A.rows ){
fprintf( stderr, "linear_equation : 正方行列でない\n" ); exit( 1 );
}
N = A.rows;
LU = make_mat( N, N );
pivot = ( int* )malloc( sizeof( int ) * N ); z = ( double* )malloc( sizeof( double ) * N );
// A -> LU に分解
lu_decomp( A.dat, LU.dat, pivot, N, N );
// Ax = LUx = y で Ux = z とおいて // Lz = y
// Ux = z を順に解く
for( int row = 0; row < N; ++row){
z[ row ] = y[ pivot[ row ] ] ; // y は pivot で入れ替えるのに注意 for( int col = 0; col < row; ++col )
z[ row ] -= LU.dat[ pivot[ row ] ][ col ] * z[ col ]; }
for( int row = N-1; row >= 0; --row){ x[ row ] = z[ row ];
for( int col = row +1; col < N; ++col )
x[ row ] -= LU.dat[ pivot[ row ] ][ col ] * x[ col ]; x[ row ] /= LU.dat[ pivot[ row ] ][ row ];
}
free_mat( LU ); free( pivot ); free( z ); }
付録
B
main
関数の例
int main() { int rows = 3; // 行数 int cols = 2; // 列数 // 行列作成 MATRIX A;A = make_mat( rows, cols );
//---// 値のセット: 行列.dat[ 行 ][ 列 ] = 値 A.dat[0][0] = 1; A.dat[0][1] = 2; A.dat[1][0] = 1; A.dat[1][1] = -3; A.dat[2][0] = -1; A.dat[2][1] = 2; //---// 内容表示 printf( "行列 A\n" ); print_mat( A ); //---// 行列 B を作成して A の内容をコピーして表示 printf( "\nコピー\n" ); MATRIX B;
B = make_mat( rows, cols ); copy_mat( A, B ); print_mat( B ); free_mat( B ); // 行列 B を削除 //---// Aの 1,2,..,rows-1 行と 1,2,...,cols-1 列の部分を B にコピー printf( "\n部分コピー\n" );
B = make_mat( rows-1, cols-1 );
copy_submat( A, B, 1, rows-1, 1, cols-1 ); print_mat( B );
free_mat( B );
//---// 転置行列
printf( "\n転置\n" );
B = make_mat( cols, rows ); // 行数と列数に注意 t_mat( A, B ); print_mat( B ); free_mat( B ); //---// 足し算、掛け算、積 printf( "\n足し算と引き算\n" ); MATRIX D;
B = make_mat( rows, cols ); D = make_mat( rows, cols );
B.dat[0][0] = 2; B.dat[0][1] = 0; B.dat[1][0] = -1; B.dat[1][1] = 2; B.dat[2][0] = 0; B.dat[2][1] = 1; printf( "\nA\n" ); print_mat( A ); printf( "\nB\n" ); print_mat( B ); plus_mat( A, B, D ); // 足し算 D = A+B printf( "\nA+B\n" ); print_mat( D ); minus_mat( A, B, D ); // 引き算 D = A-B printf( "\nA-B\n" ); print_mat( D ); printf( "\n積\n" ); MATRIX C,E;
C = make_mat( cols, rows ); // 行数と列数に注意 E = make_mat( rows, rows ); // 行数と列数に注意 C.dat[0][0] = -1;
C.dat[0][1] = 0; C.dat[0][2] = 2;
C.dat[1][1] = 2; C.dat[1][2] = 0; printf( "\nA\n" ); print_mat( A ); printf( "\nC\n" ); print_mat( C ); prod_mat( A, C, E ); // 積 E = A*C printf( "\nA*C\n" ); print_mat( E ); free_mat( A ); free_mat( B ); free_mat( C ); free_mat( D ); free_mat( E ); //---// 逆行列 printf( "\n逆行列\n" ); cols = 3; rows = 3;
A = make_mat( rows, cols ); B = make_mat( rows, cols );
A.dat[0][0] = 1; A.dat[0][1] = 2; A.dat[0][2] = 1; A.dat[1][0] = 2; A.dat[1][1] = 3; A.dat[1][2] = 1; A.dat[2][0] = 1; A.dat[2][1] = 2; A.dat[2][2] = 0; inverse_mat( A, B ); printf( "\nA\n" ); print_mat( A ); printf( "\nAの逆行列\n" ); print_mat( B ); printf( "\nA * (Aの逆行列)\n" );
C = make_mat( rows, cols ); prod_mat( A, B, C ); print_mat( C ); free_mat( A ); free_mat( B ); free_mat( C ); return 0; }
付録
C
出力結果
行列 A 1.000 2.000 1.000 -3.000 -1.000 2.000 コピー 1.000 2.000 1.000 -3.000 -1.000 2.000 部分コピー -3.000 2.000 転置 1.000 1.000 -1.000 2.000 -3.000 2.000 足し算と引き算 A 1.000 2.000 1.000 -3.000 -1.000 2.000 B 2.000 0.000 -1.000 2.000 0.000 1.000 A+B 3.000 2.000 0.000 -1.000 -1.000 3.000 A-B-1.000 2.000 2.000 -5.000 -1.000 1.000 積 A 1.000 2.000 1.000 -3.000 -1.000 2.000 C -1.000 0.000 2.000 -1.000 2.000 0.000 A*C -3.000 4.000 2.000 2.000 -6.000 2.000 -1.000 4.000 -2.000 逆行列 A 1.000 2.000 1.000 2.000 3.000 1.000 1.000 2.000 0.000 Aの逆行列 -2.000 2.000 -1.000 1.000 -1.000 1.000 1.000 -0.000 -1.000 A * (Aの逆行列) 1.000 0.000 0.000 0.000 1.000 0.000 0.000 0.000 1.000