原田恒司 ∗ 九州大学基幹教育院 (最終更新日: December 27, 2015) いろいろな例を通してイメージをつかむ。後半はちょっと難しくなってしまった。 CONTENTS I. 勾配 1 II. 発散 2 III. 回転 2 IV. 線積分 3 V. 面積分 5 VI. 体積分 6 VII. ガウスの定理 7 VIII. ストークスの定理 9 I. 勾配 1 変数の関数 f (x) の微分 f′(x) が、y = f (x) のグラフの x における傾きをあらわしていることはよく知っているだ ろう。スカラー場 ϕ(r) の勾配 (gradient)∇ϕ(r) (gradϕ(r) とも書く) も、傾きを表すものだが、ベクトル (場) として 「方向」の情報も含んでいる。∇ϕ(r) の方向は、r におい て最も登りが急な方向である。その「大きさ」は傾きの大 きさである。
x
y
∂ϕ ∂x ∂ϕ ∂yϕ
図1. 勾配の幾何学的意味。教科書p.42 [注意!]参照。 実際、∇ϕ(r) というベクトルは、ϕ(r) を通り ϕ を一定 にする面 (2 次元ならば「等高線」) に垂直である。教科書 p.42[例題 5.2] を見よ。 ∗harada(AT)artsci.kyushu-u.ac.jp デカルト座標 r = xi + yj + zk を用いて勾配を表すと ∇ϕ(r) = ∂ϕ(r) ∂x i + ∂ϕ(r) ∂y j + ∂ϕ(r) ∂z k (1.1) となる。 勾配はスカラー場 ϕ(r) からベクトル場 ∇ϕ(r) を作る ことに注意。∇ を ∇ = i ∂ ∂x+ j ∂ ∂y + k ∂ ∂z (1.2) というベクトルであると考えると、∇ϕ(r) はベクトル ∇ のスカラー場 ϕ(r) 「倍」とみなすこともできる。もちろ ん∇ は微分演算子なので、順序は重要であるが。 いくつか具体例を見てみよう。 ϕ(r) = x の場合 ∇ϕ(r) = i (1.3) ϕ(r) = x は y、z に関係なく、一様に x の正の方向に進 むと大きくなる。∇ϕ(r) はそのことをよく表しているこ とに注意。つまり、i (x 方向の単位ベクトル) は傾きが最 大の方向を表し、位置 (座標) に依存しない。 ϕ(r) = x2 の場合 ∇ϕ(r) = 2xi (1.4) こんどは y、z に関係ないのは同じだが、x 方向に進んだ ときの大きくなりかたが一様ではない。x > 0 では x の正 の方向が最も傾きが大きくなる方向であるが、x < 0 では x の負の方向が最も傾きが大きくなる方向である。傾きは x = 0 から遠ざかるにしたがって大きくなる。これはちょ うど y = x2 のグラフの傾きの場合と同じである。∇ϕ(r) は dy/dx とは違い、ベクトル (場) であることに注意。 ϕ(r) = x2+ y2+ z2 の場合 ∇ϕ(r) = 2xi + 2yj + 2zk = 2r (1.5) ϕ(r) は原点からの距離の 2 乗で、その「等高面」は原点 を中心とした球面である。上に述べたように、∇ϕ(r) は 「等高面」に垂直である。実際、∇ϕ は r に比例している。 ϕ(r) は原点から離れるにしたがって、距離の 2 乗で大き くなる。つまり大きくなる割合 (微分!) は、距離に比例す る。このことは|∇ϕ(r)| が r に比例することと対応して いる。II. 発散
ベクトル場 A(r) というのは、空間の各点にベクトル が割り当てられたもの。その全体は一種の「流れ」のよ うなものだ。その「流れ」の湧き出しや吸い込みが発散 (divergence)∇ · A(r) (divA(r) とも書く) の幾何学的イ メージである。A = Axi + Ayj + Azk とすると、 ∇ · A(r) = ∂Ax(r) ∂x + ∂Ay(r) ∂y + ∂Az(r) ∂z (2.1) 発散はベクトル場 A(r) からスカラー場∇ · A(r) を作 ることに注意。∇ をベクトルと見ると、発散はベクトル ∇ とベクトル場 A(r) との内積とみなすことができる。(実 際そういう書き方をしている。) いくつか具体例を見てみよう。 A(r) = ai + bj + ck (a, b, c は定数) の場合 ∇ · A(r) = 0 (2.2) このベクトル場は、すべての点で同じ方向、同じ大きさの ベクトルを与える。このベクトル場に対して (直感的にも 明かだと思うが) 発散はゼロである。湧き出しも吸い込み もない。 A(r) = xi + yj + zk = r の場合 ∇ · A(r) = 3 (2.3) ベクトル場 A(r) は原点から放射状に出て、遠ざかるにつ れてその大きさが大きくなっている。縮まない流体 (水は 近似的にそうみなせる) の流れの速度の場合にはそのよう なことは起らない。このような「流れ」をつくるためには、 空間の各点で流体を補給してやらなくてはならない。つま り、空間の各点に湧き出しが必要である。それが∇·A > 0 ということである。このことを理解するために、空間のあ る点に小さな閉曲面を考え、この閉曲面に入り込む「流 れ」と、出ていく「流れ」を比べよう1。図 2 を見よ。「流 れ」は等方的なので、r = r0 と r = r0+ ∆r (∆r は微小) の 2 つの球面に挟まれた球殻に流れ込む量と流れ出る量を 考えればよい。A は球面に垂直であることに注意しよう。 |A(r0)| = r0、|A(r0+ ∆r)| = r0+ ∆r であるから、この球 殻には 4πr2 0× r0だけ流れ込み、4π(r0+ ∆r)2× (r0+ ∆r) だけ流れ出している。その差は 4π(r0+ ∆r)3− 4πr03≈ 12πr 2 0∆r (2.4) である。(∆r の 2 次以上は高次の微小量なので無視した。) これだけの湧き出しがあるということだ。この球殻の体積 は 4πr2 0∆r なので、単位体積あたり 3 の湧き出しがある ことになる。これが∇ · A = 3 の意味である。 1 これから行なうのは面積分の特別な場合である。 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 図2. 発散(湧き出し)のある場合。図の点線は球殻の一部を表 す。わかりやすいように、2次元的に表した。赤い閉曲線(3次 元的には閉曲面)で囲まれた部分に流れ込む量と、そこから流れ 出す量とを比べる。側面(中心からの角度が一定の線)には流れ 込みも流れ出しもないことに注意。 A(r) = yi− xj の場合 ∇ · A(r) = 0 (2.5) ベクトル場 A(r) は z 軸を中心とした円柱状に回転して いる「流れ」に対応している。このような「流れ」では閉 曲面に入ってくる「流れ」と出ていく「流れ」がつりあっ ていて、湧き出しも吸い込みも必要ない。図 3 参照。 教科書では万有引力と関連させて付録 E で発散が説明 されている。p.280 から p.283 を見よ。 III. 回転
回転(rotation)∇ × A(r) (rotA(r) または curlA(r)
とも書く) は「流れ」で言えば渦を表している。 ∇ × A(r) = ( ∂Az(r) ∂y − ∂Ay(r) ∂z ) i + ( ∂Ax(r) ∂z − ∂Az(r) ∂x ) j + ( ∂Ay(r) ∂x − ∂Ax(r) ∂y ) k (3.1) あるいは行列式の書き方を使って、 ∇ · A(r) = i j k ∂ ∂x ∂ ∂y ∂ ∂z Ax(r) Ay(r) Az(r) (3.2) とも表せる。回転はベクトル場 A(r) から(擬)ベクトル 場∇ × A(r) を作ることに注意。∇ をベクトルと見ると、
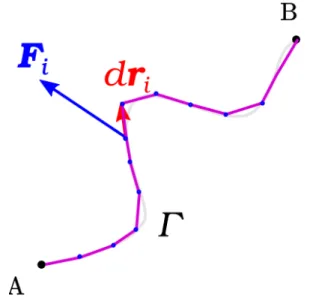
0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 図3. 今度は球面を通過する流れ込み、流れ出しがない。側面か らの流れ込みは、反対の側面からの流れ出しと釣り合っている。 この流れでは湧き出しはない。 回転はベクトル∇ とベクトル場 A(r) の外積とみなすこ とができる。(実際そういう書き方をしている。) いくつか具体例を見てみよう。 A(r) = ai + bj + ck (a, b, c は定数) の場合 ∇ × A(r) = 0 (3.3) 一様な「流れ」に対して渦はない。 A(r) = xi + yj + zk = r の場合 ∇ × A(r) = 0 (3.4) ベクトル場 A(r) は原点から放射状に出ている「流れ」で ある。直感的にもわかると思うが、このような「流れ」に は渦はない。 A(r) = yi− xj の場合 ∇ × A(r) = −2k (3.5) この「流れ」には z 軸方向に回転軸を持つ渦がある。注 意しなくてはならないのは、原点にだけ渦があるのではな く、空間のいたるところに渦がある(∇ × A(r) はすべて の r に対してゼロではない)ということである。ちょっ と直感に反するかも知れないが、これは普通の流体ではこ のような「流れ」を作ることができないという事実と対応 している。この「流れ」は z 軸から離れていくにしたがっ て、どんどん速くなっていく。 図4. 力の場F がする仕事 このことを理解するために、z が一定の面内で、図 3 の ような閉曲線を考えよう2。渦があるというのは、この閉 曲線に沿っての「流れ」がゼロでないことを意味する。z 軸 から見たときのこの閉曲線の角度の開きが ∆θ (微小量) で あるとすると、外側 (r = r0+ ∆r) での閉曲線に沿った「流 れ」は|A| = (r0+ ∆r) なので−(r0+ ∆r)∆θ× (r0+ ∆r) であり、内側では|A| = r0なので r0∆θ× r0である。(曲 線の長さ×「流れ」を向きづけして計算した。)側面では曲 線と「流れ」が垂直なので、曲線に沿った「流れ」がゼロ であることに注意。これらから閉曲線に沿った「流れ」は −(r0+ ∆r)2∆θ + r20∆θ≈ −2r0∆r∆θ (3.6) である。この閉曲線で囲まれた面積は r0∆r∆θ であるの で、曲線に沿った「流れ」は単位面積当たり−2 である。 これが∇ × A = −2k の意味である。 IV. 線積分 線積分については教科書 p.39 から p.44 に説明してあ る。力の場3 F (r) の中で物体を曲線 Γ に沿って A から B まで移動させる場合(図 4 参照)、その力の場がする仕 事は W = ˆ Γ F (r)· dr (4.1) で与えられる。 大きさ F の(一定の)力がはたらいている物体を l だけ 移動させた時に、力がする仕事は F l cos θ で与えられる、 2これから行うのは線積分の特別な場合である。 3空間の各点で、物体が受ける力が決まっている場合、力の場があると いう。例えば、地上近くでは物体がどこにあっても、物体の質量を m とすると物体は mg という力を受ける。この力の場を(一様な)重力 場という。
図5. 図4の曲線Γを折れ線で近似する。折れ線ごとにFi· dri を計算し、その和をとる。 ということを高校の時に学んだはずである。(ただし、θ は 力の働く方向と移動方向との間の角度である。) これはそ の一般化である。そのことをもっとはっきりさせるには、 曲線 Γ を一つ一つが非常に小さい折れ線で近似して考え ると良い。図 5 参照。それぞれの折れ線は十分短いので、 その区間でははたらく力は一定であると近似してよい。i 番目の折れ線にはたらく力を Fi、その折れ線に沿った移 動を表すベクトルを driとすると、この折れ線での仕事は Fi· dri で与えられる。和 ∑ iFi· dri を考えよう。折れ線 の長さをどんどん短くしていくと、どんどん「曲線に沿っ た」積分に近づいていく。この極限が式 (4.1) である。 線積分 (4.1) の結果は一般に曲線 Γ に依存することに 注意しなくてはならない。教科書 p.40 [例題 5.1] を参照 せよ。 第 III 章で A(r) = yi− xj の場合に閉曲線に沿っての 「流れ」を計算したが、これは線積分に他ならない。閉曲 線を Γc とすると ˛ Γc A(r)· dr (4.2) と表される。記号¸ は閉じた経路に沿った積分であるこ とを強調するために´ と区別して用いた。 いくつか具体例を計算しよう。 A(r) = ai + bj + ck (a, b, c は定数) の場合 O(0, 0, 0)、A(1, 0, 0)、B(0, 1, 0)、C(1, 1, 0) とする。ま ず OAC という折れ線にそって積分しよう。 ˆ OAC A(r)· dr = ˆ 1 0 adx + ˆ 1 0 bdy = a + b (4.3) 第 1 項が OA に沿った積分、第 2 項が AC に沿った積分であ る。OA 上では dr = dxi とかけるので、A(r)·dr = (ai+
bj + ck)· dxi = adx となる。一方、AC 上では dr = dyj
とかけるので、A(r)· dr = (ai + bj + ck) · dyj = bdy と
なる。 同様に OBC に沿って積分すると ˆ OAC A(r)· dr = ˆ 1 0 bdy + ˆ 1 0 adx = b + a (4.4) となる。第 1 項が OB に沿った積分、第 2 項が BC に沿っ た積分である。今の場合 OAC に沿った積分と、OBC に 沿った積分の結果は一致している。 今示したのは単に 2 つの経路に対して積分値が一致す ることだけであるが、実際は O と A を結ぶ任意のに対 して積分結果は同じになる。その説明は、教科書の p.43 から p.44、p.277 から p.279 に説明してある。すなわち、 ∇ × A(r) = 0 が成り立つならば、始点と終点が同一の 任意の 2 つの経路に対して線積分が一致する。今の場合 ∇ × A(r) = 0 であるから、任意の経路に対して線積分の 値は同一である。 A(r) = xi + yj + zk = r の場合 第 III 章で示したように、このベクトル場に対して回転 はゼロであるので、始点と終点が同一の任意の経路に対し て線積分の値は同じである。実際、経路 OAC 沿った積 分は ˆ OAC A(r)· dr = ˆ 1 0 xdx + ˆ 1 0 ydy = 1 2+ 1 2 = 1 (4.5) となり、経路 0BC に対しても同様であることはすぐにわ かるだろう。ここでは OC と直線的に C に至る経路に対 して積分を計算してみよう。OC 上の点 r はパラメタ t を 用いて r(t) = t(i + j) (0≤ t ≤ 1) と表すことができる。 それゆえ、dr = (i + j)dt と書くことができる。線積分は ˆ OC A(r)· dr = ˆ 1 0 (ti + tj + 0k)· (i + j)dt = ˆ 1 0 2tdt = 1 (4.6) となって、積分値は一致する。 A(r) = yi− xj の場合 この場合は ∇ × A(r) ̸= 0 であるので、経路によって 積分値が違う。実際、 ˆ OAC A(r)· dr = ˆ 1 0 (0i− xj) · dxi + ˆ 1 0 (yi− 1j) · dyj =−1 (4.7) であるが、一方 ˆ OBC A(r)· dr = ˆ 1 0 (yi− 0j) · dyj + ˆ 1 0 (1i− xj) · dxi = 1 (4.8) となって一致しない。
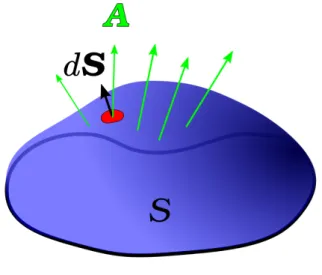
図6. 面積分 A(r) =∇ϕ(r) の場合 ベクトル場がなにかあるスカラー場の勾配で書かれると き、線積分はその端点の値だけで決まる。 ˆ B A ∇ϕ(r) · dr = ϕ(rA)− ϕ(rB) (4.9) この式の証明は教科書 p.43 を見ればよい。 これは直線上の積分に対する公式 ˆ b a df (x) dx dx = f (b)− f(a) (4.10) の一般化とみなせる。 ベクトル場が A(r) =∇ · ϕ(r) で与えられているとき、 ∇ × A(r) = 0 である。これは定義を用いて具体的に計算 すればすぐに示すことができる。 ベクトル場 A(r) = ai + bj + ck は ϕ(x, y, z) = ax + by + cz の勾配として表されるので、その線積分は経路に 依存しない。ベクトル場 A(r) = r は ϕ(r) = 1 2|r| 2 の勾 配として表されるので、その線積分は経路に依存しない。 一方、ベクトル場 A(r) = yi− xj は何かあるスカラー場 の勾配としては表すことができない。 V. 面積分 面積分はベクトル場で表される「流れ」が、その面をど れだけ通過するかを表すものだ。それゆえ、面をどちら側 に通過するか、という向きづけが問題になる。ベクトル場 A(r) の(向きづけられた)曲面 S 上の面積分は ¨ S A(r)· dS (5.1) と書かれる。A(r)· dS はベクトル場 A(r) と面素 dS と の内積を表している。面を通過する量が問題なのだから、 ベクトル場の面に垂直な成分を取り出す必要がある。内積 はその操作を表している。 ちょうど曲線上の線積分を折れ線での和の極限として定 義したように、曲面上の面積分は、曲面を微小な平面で分 割して、それぞれの平面上での積分の和の極限として定義 することができる。面素 dS はそのような微小な面だと 考えてよい。面素はベクトルであることに注意。その大き さは面積であり、その方向はその面に垂直な方向である。 (図 6 参照。)向きづけはこの方向をどちら向きにとるかと いうことである。面に垂直な方向と、A との内積は、A の 面に垂直な成分を取り出す。 いくつか具体例を計算しよう。 A(r) = ai + bj + ck (a, b, c は定数) の場合 z = 0 上の正方形 OACB (z 軸の正方向を面の向き とする)上で積分してみよう。積分範囲は 0 ≤ x ≤ 1、 0≤ y ≤ 1 で、x と y は独立に計算できる。dS = dxdyk とかけるので、 ˆ 1 0 dx ˆ 1 0 dy(ai + bj + ck)· k = c (5.2) を得る。 面素の表し方の練習として、原点を中心とした半径 1 の 球面のうち、z≥ 0 の部分で定義される半球面上で積分し てみよう。(球面の外に向かう向きを正とする。) 今度は極 座標(球座標ともいう)を用いるのが便利である。極座標 については p.98 [例題 11.1] を参照せよ。球面上では
r = er= sin θ cos ϕi + sin θ sin ϕj + cos θk (5.3) と表されることに注意。er は r 方向の単位ベクトルであ る。今の場合 r = |r| = 1 であることに注意。r におけ る面素 dS は、極座標を用いて dS = sin θdθdϕerと表せ る4。それゆえ ¨ 半球面 A(r)· dS = ˆ π/2 0 sin θdθ ˆ 2π 0 dϕ(ai + bj + ck)· er = ˆ π/2 0 sin θdθ ˆ 2π 0
dϕ(a sin θ cos ϕ
+ b sin θ sin ϕ + c cos θ) = 2πc ˆ π/2 0 sin θ cos θdθ = πc (5.4) を得る。この結果は (半径 1 の円の面積)×c とみなせるこ とに注意しよう。上の正方形 OACB の場合にも、(1 辺の 長さが 1 の正方形の面積)×c とみなせる。 実は今のベクトル場の場合、曲面の形に依らず面積分の 結果は (境界となる (z = (一定) の) 曲線で囲まれた平面 図形の面積)×c となる。境界を同じくする 2 つの曲面 S1 4半径が R の球面を考えていたのなら dS = R2sin θdθdϕ e rである。
と S2 を合わせると、ひとつの閉曲面が作られることに注 意しよう。ただし、一方の曲面の向きづけを逆にする必要 がある。S2 の向きづけを逆にしたものを ¯S2 と書くこと にしよう。定義より ¨ ¯ S2 A(r)· dS = − ¨ S2 A(r)· dS (5.5) が成り立つ。閉曲面を S = S1∪ ¯S2 と呼ぼう。このベク トル場の発散がゼロなので、この閉曲面 S に入る「流れ」 と出て行く「流れ」の量は等しく、それゆえにこの閉曲面 にわたる積分はゼロになる。 ‹ S A(r)·dS = ¨ S1 A(r)·dS + ¨ ¯ S2 A(r)·dS = 0 (5.6) すなわち、 ¨ S1 A(r)· dS = ¨ S2 A(r)· dS (5.7) となる。 A(r) = xi + yj + zk = r の場合 このベクトル場を、原点を中心とする z = 0 上の半径 1 の円上で積分してみよう。面の向きは z 軸の正の向きと する。2 次元極座標 (x = r cos ϕ, y = r sin ϕ) を用いると、 dS = rdrdϕk と表すことができる。 ¨ 円 A(r)· dS = ˆ 1 0 rdr ˆ 2π 0
dϕ(r cos ϕi + r sin ϕj + 0k)· k
= 0 (5.8) この結果は「流れ」が z = 0 面内にあり、面を通過してい かないことからもわかる。 今度は原点を中心とし、z≥ 0 の半径 1 の半球面上で積 分しよう。球面上では A(r) = er となることに注意する と計算は簡単になる。 ¨ 半球面 A(r)· dS = ˆ π/2 0 sin θdθ ˆ 2π 0 dϕ er· er = 2π (5.9) つまり、今度は境界が同じであっても、異なる曲面に対し ては積分値は異なるのである。このベクトル場に対して、 ∇ · A(r) = 3 であったことを思い出そう。そして、これ は単位体積あたり 3 の湧き出しがあることを意味してい る。z = 0 での円と、この半球面で作られる閉曲面を考え ると、その閉曲面で囲まれる体積は 2π/3 である。それゆ え、この体積中の湧き出しの総量は (2π/3)× 3 = 2π で ある。まさしくこの量を式 (5.8) と (5.9) で見ているので ある。 図7. 極座標での体積要素 VI. 体積分 体積分というのは、3 次元的なひろがりを持った図形に わたって、積分を行なうものをいう。図形の形に応じて積 分範囲を適切に考えることが重要である。 よく見かける混乱は、(一般の) 体積分と、体積を求める 積分との混同である。体積も体積分によって求まるが、そ れは (被積分関数が 1 という) 特殊な体積分である。 「図形の形に応じて」積分範囲を決めるため、普通のデ カルト座標での積分ばかりでなく、極座標や円柱座標を用 いた積分が用いられる。極座標については教科書の p.98 に、円柱座標については教科書の p.114 に説明がある。 一辺の長さが a である立方体の体積 これはデカルト座標で計算するのが便利である。体積要 素 dv は dv = dxdydz で与えられる。dv のことを d3r と か d3r などと書くこともある。 V立方体= ˚ 立方体 dv = ˆ a 0 dx ˆ a 0 dy ˆ a 0 dz = a3 (6.1) 被積分関数 (いまの場合 1) および積分領域が変数に依ら ないので積分は 3 つの 1 次元積分の積として計算できる。 半径が R である球体の体積 これは極座標を用いて計算するのが便利である。体積要 素 dv = r2sin θdrdθdϕ で与えられる。図 7 を見よ。それ
ゆえ V球体= ˚ 球体 dv = ˆ R 0 r2dr ˆ π 0 sin θdθ ˆ 2π 0 dϕ =R 3 3 · 2 · 2π = 4π 3 R 3 (6.2) を得る。この問題では被積分関数は 1 であるが、体積要素 が座標に依存していることに注意。 球の体積をデカルト座標で計算することもできる。その ために、球の z が一定の面で切ったときの断面を考えよ う。この断面は、半径√R2− z2の円である。z と z + dz の間では、半径 rz≡√R2− z2、高さ dz の円柱でよく近 似でき、この近似は dz が小さいほど精密になる。今度は その円を y が一定の線で切ってみよう。そのときの長さは 2√r2 z− y2= 2 √ R2− y2− z2で与えられる。y と y + dy の間では、長さ 2√R2− y2− z2、幅 dy の長方形でよく 近似でき、この近似は dy が小さいほど精密である。次に この長方形の長さは、(自明であるが)−√R2− y2− z2か ら +√R2− y2− z2まで x で (1 を) 積分することによっ て求まる。 V球体= ˆ R −R dz · (z = (一定) の面で切ったときの断面積) = ˆ R −R dz ˆ √ R2−z2 −√R2−z2 dy · (円を y = (一定) の線で切ったときの線の長さ) = ˆ R −R dz ˆ √ R2−z2 −√R2−z2 dy ˆ √R2−y2−z2 −√R2−y2−z2 dx (6.3) ここでは、積分領域が積分変数に依存することに注意。ま ず x で積分すると、その積分結果は y と z の関数となり、 それを y で積分すると z の関数となり、最後に z で積分 して結果が得られる。実際に計算してみると、 V球体= ˆ R −R dz ˆ √ R2−z2 −√R2−z2 dy ˆ √R2−y2−z2 −√R2−y2−z2 dx = 2 ˆ R −R dz ˆ √ R2−z2 −√R2−z2 dy√R2− y2− z2 (y =√R2− z2sin t とおくと) = 2 ˆ R −R dz ˆ π 2 −π 2 √ R2− z2cos θdθ ·√R2− z2√1− sin2 θ = 2 ˆ R −R dz(R2− z2) ˆ π 2 −π 2 cos2θdθ = 2·4 3R 3· π 2 = 4π 3 R 3 (6.4) のように求まる。 体積分については、教科書第 13 章の例題で他の例を学 ぶとよい。 VII. ガウスの定理 ガウスの定理は、発散のイメージを得るために既にある 程度使ってきている。ベクトル場 A(r) の閉曲面 S 上の 面積分と、その閉曲面によって囲まれた体積 V について の積分と結びつける。 ‹ S A(r)· dS = ˚ V ∇ · A(r) dv (7.1) ガウスの定理の導出については、教科書 p.281 から p.283 を見よ。 ベクトル場を「流れ」とみると、左辺の面積分は閉曲面 S から出ていく流れの量から入っていく流れの量を引いた ものを表す。それは (右辺で表される) 閉曲面で囲まれた 部分での湧き出し (湧き出しの総和から吸い込みの総和を 引いたもの) に等しい。 電磁気学での応用では、「流れ」は電場 (電気力線) で、 湧き出しは電荷になっている。電荷密度 ρ(r) が与えられ ているとき、その電荷分布によって作られる電場 E(r) は 重ね合せの原理から E(r) = 1 4πϵ0 ˚ ρ(r′)(r− r′) |r − r′|3 d 3r′ (7.2) で与えられる。この電場の発散∇ · E(r) を計算してみよ う。積分は r′ についてのものなので、r についての微分 ∇ は積分の中に作用し、 ∇ · E(r) = 1 4πϵ0 ˚ ρ(r′)∇ · ( (r− r′) |r − r′|3 ) d3r′ (7.3) ここで、括弧の中の量は r = r′ での振舞いが悪いので、 かわりに ∇ · ( r− r′ [|r − r′|2+ ϵ2]32 ) (7.4) を考えることにしよう。ここで ϵ は正の小さな定数である。 ∂ ∂x ( x− x′ [(x− x′)2+ ∆2]32 ) = 1 [(x− x′)2+ ∆2]32 − 3 (x− x′)2 [(x− x′)2+ ∆2]52 (7.5) であるから、 ∇ · ( r− r′ [|r − r′|2+ ϵ2]32 ) = 3 [|r − r′|2+ ϵ2]32 − 3|r − r′|2 [|r − r′|2+ ϵ2]52 = 3ϵ 2 [|r − r′|2+ ϵ2]52 (7.6)
を得る。 右辺に現れる関数は実におもしろい性質を持っている。 r̸= r′ のとき ϵ→ 0 とするとゼロになる。一方、r = r′ のときには、ϵ→ 0 とすると 3/ϵ3 のように振舞い、無限 大になる。つまり、r = r′ の近傍だけが重要で、それ以 外ではゼロと考えてよい。それゆえ、 ˚ ρ(r′)∇ · ( (r− r′) |r − r′|3 ) d3r′ ≈ ρ(r) ˚ 3ϵ2 [|r − r′|2+ ϵ2]52 d3r′ (7.7) と近似してよい5。この近似は ϵ が小さければ小さいほど 精度がよい。 最後の積分は、積分変数変換 R = r− r′ を行なってか ら、極座標を用いて ˚ 3ϵ2 [|r − r′|2+ ϵ2]52 d3r′ = 12πϵ2 ˆ ∞ 0 R2dR [R2+ ϵ2]52 (7.8) となる。R = ϵ tan t と変数変換すると、dR = ϵdt/ cos2t、 ϵ2R2 [R2+ ϵ2]52 = ϵ 4tan2t ϵ5[1 + tan2t]52 =1 ϵtan 2t cos5t = 1 ϵsin 2 t cos3t (7.9) であるから、 ϵ2 ˆ ∞ 0 R2dR [R2+ ϵ2]52 = ˆ π 2 0 cos t dt sin2t = 1 3 (7.10) -1 1 2 3 5 10 15 20 25 図8.式(7.7)のイメージ。なめらかな関数と鋭いピークを持つ 関数。 5 具体的な例で見てみよう。図 8 には ϵ = 10−3 とたときの y = 3ϵ2/[(x− 1)2+ ϵ2]52 となめらかな関数の例として y = x2+ 2x + 4 を描いている。この二つの関数の積を積分を考えてみよう。鋭いピー クを持つ関数はピークの近傍以外ではほとんどゼロなので、被積分関 数もほとんどゼロで積分はほとんどゼロになる。ピークは十分狭いの で、そこではなめらかな関数はほとんど一定値 (今の例では 7) をと る。それゆえ、ピークの近傍では被積分関数は、ピークの位置でのな めらかな関数の値 (定数) かける鋭いピークを持つ関数で良く近似さ れる。 を得る。結果が ϵ に依らないことに注意せよ。ϵ はいくら でも小さくすることができる。 以上から ∇ · E(r) = ρ(r) ϵ0 (7.11) を得る。これは (微分形の) ガウスの法則と呼ばれる。(各 点における) 電場の湧き出しは (その点での) 電荷密度で与 えられるということの数学的表現である。 ガウスの定理を用いると ‹ S E(r)· dS = 1 ϵ0 ˚ V ρ(r)d3r (7.12) が得られる。右辺の積分は、V に含まれる全電荷 Q を 表す。 ‹ S E(r)· dS = Q ϵ0 (7.13) これが教科書 p.142 の (積分形の) ガウスの法則である。 ガウスの定理はどんな複雑な閉曲面に対しても成立する が、面積分を具体的に計算できるのは簡単な閉曲面に限ら れる。閉曲面がベクトル場の持つ対称性と同じ対称性を持 つ場合には特に簡単に計算できる。 無限に長い直線上に一様に分布した電荷がつくる電場 単位長さあたりの電荷 (線密度) を λ とする。この直線 が z 軸に一致するとして、直線から r だけ離れたところ での電場 E(r) を求めよう。まず、問題の対称性から、電 場は z には依らず、z 軸に対して軸対称であることがわ かる。つまり、z 軸からの距離のみに依存する。(だから E(r) とは書かず、E(r) と書いた。) 電場 E(r) は (円柱 座標での) r 方向、つまり z 軸から遠ざかる方向の成分の みをもつ。つまり、E(r) = Er(r)er と書ける。ここで er は円柱座標での r 方向の単位ベクトルを表す。 ベクトル場 E(r) の対称性を考慮すると、z 軸を対称軸 とした (フタのついた) 円筒を考えるのがよいことがわか る。この円筒の長さを L、半径を a としよう。円筒の上 下のフタの部分では、ベクトル場 E(r) は面と平行である から、 ¨ フタ E(r)· dS = 0 (7.14) となる。円筒の側面では、ベクトル場 E(r) は一定の大き さ (Er(a)) で、面に垂直であるから、 ¨ 側面
E(r)· dS = 2πaL × Er(a) (7.15) となる。2πaL は側面の面積である。以上より
‹
円筒
E(r)· dS = 2πrL × Er(a) (7.16) を得る。
一方、この閉曲面に含まれる電荷は Q = λL で与えら れる。それゆえ、ガウスの法則から、 2πaL× Er(a) = λL ϵ0 (7.17) となる。すなわち Er(a) = λ/(2πϵ0a)、よって E(r) = λ 2πϵ0r er (7.18) を得る。 VIII. ストークスの定理 ガウスの定理を発散のイメージの説明のために用いたの と同様に、ストークスの定理は回転のイメージの説明のた め、既に暗黙のうちに用いている。ベクトル場 A(r) の閉 曲線 Γcに沿っての線積分と、その閉曲線を境界とする (向 き付けられた) 面 S 上の面積分とを結びつける。 ˛ Γc A(r)· dr = ¨ S (∇ × A(r)) · dS (8.1) ストークスの定理の導出は教科書 p.277 から p.279 を見よ。 ベクトル場を「流れ」とみると、左辺の線積分は、閉曲 線に沿ってどれだけ流れているかを表している。渦がなけ ればそれは (打ち消しあって) ゼロになる。右辺は閉曲線 に囲まれている面を通過する渦糸を数えている。 電磁気学への応用では、「流れ」は磁場に対応し、その 回転を作り出す原因である渦糸は電流密度 (単位体積あた りに流れる電流) に対応する。 z 軸に沿って正の向きに一定の電流 I が流れている場 合を考えよう。ビオ-サバールの法則 (教科書 p.177 から p.179) B(r) = µ0 4π ˆ C Ids× (r − r′) |r − r′|3 (8.2) から、この電流が位置ベクトル r = xi + yj + zk で表さ れる位置に作る磁場 B(r) は6 B(r) = µ0 4π ˆ ∞ −∞ Idz′k× (xi + yj + (z − z′)k) [x2+ y2+ (z− z′)2]32 =µ0I 4π (−yi + xj) ˆ ∞ −∞ dz′ [x2+ y2+ (z− z′)2]32 = µ0I 4π(x2+ y2)(−yi + xj) ˆ π 2 −π 2 cos θdθ = µ0I 2π (x2+ y2)(−yi + xj) (8.3) となる。磁場 B(r) の方向は、電流の方向 k と r の方向 i との外積の方向である。 6 正しくは磁束密度と言うべきだが、このノートでは B を磁場と呼ぶ。 このベクトル場に対して、z 軸に垂直な平面内で、z 軸 を中心とする半径 a の円に沿って、z 軸の正の向きに対し て右ねじの方向に積分しよう。 ˛ 円 B(r)· dr (8.4) 上に見たように、磁場 b(r) と線素 dr は平行であるので、 ˛ 円 B(r)· dr = µ0I 2πa ˆ 2π 0 adϕ = µ0I (8.5) 左辺の積分は z 軸を囲んでいれば、円形の閉曲線でなく ても同じ結果になる。また、電流も直線でなくても閉曲線 によって囲まれていれば同じ結果になる。それがアンペー ルの法則である。 ベクトル場 (8.3) の回転を計算しよう。ただし、この表 式は x = y = 0 での振舞いが悪いので、以前やったよう に、微小な正数 ϵ を導入して B(r) = µ0I 2π (x2+ y2+ ϵ2)(−yi + xj) (8.6) として考えよう。Bz = 0 および、Bx と By が z に依存 しないことから、 ∇ × B(r) = ( ∂By ∂x − ∂Bx ∂y ) k = µ0I 2π 2ϵ2 (x2+ y2+ ϵ2)2k (8.7) を得る。ここに現れる関数もおもしろい性質を持っている。 x2+ y2̸= 0 であれば ϵ → 0 でゼロになるが、x2+ y2= 0 であれば ϵ→ 0 で発散する。これを半径 a の円上で積分 してみよう。円柱座標を用いて dS = rdrdϕk と書ける ので ¨ 円 (∇ × B(r)) · dS = µ0I ˆ a 0 2ϵ2rdr (r2+ ϵ2)2 = µ0I a2 a2+ ϵ2 (8.8) となる。ここで ϵ→ 0 の極限は問題なくとれて、µ0I を 得る。 上では導線のような細い線に沿って一定の電流が流れる 単純な場合を考えたが、これは電場を考えるときに点電荷 を考えることに対応している。より一般的な電荷分布に対 して作られる電場があるように、より一般的な電流の流れ によって作られる磁場を考えることができる。一般的な電 流の流れは電流密度 ie(r) というベクトル場によって記述 される7。位置 r において流れる電流の方向 が ie(r) の 方向であり、その方向に垂直な面の単位面積あたりに流れ る電流の大きさが ie(r) の大きさである。 7教科書では電流密度を単に i(r) と表しているが、デカルト座標での 基底ベクトル i との混乱を避けるため、添字 e を付けた。
(証明はしないが) 一般的な電流密度ベクトル場 ie(r) が 与えられたとき、ビオ-サバールの法則は B(r) = µ0 4π ˚ ie(r′)× (r − r′) |r − r′|3 d 3r′ (8.9) と一般化される。 具体的な電流密度ベクトル場の例として ie(r) = 1 2π 2Iϵ2 (x2+ y2+ ϵ2)2k (8.10) を考えよう。これは (I > 0 とすると) z の正方向に流れ る電流を表し、z 軸の近傍でのみ大きな値をとる。x-y 平 面を通過する電流の総量は ¨ x-y 平面 ie(r)· dS = ˆ ∞ 0 rdr 2Iϵ 2 (r2+ ϵ2)2 = I (8.11) となるので、この電流密度ベクトル場は、ϵ が十分小さけ れば、z 軸上を流れる電流のよい近似になっている。 式 (8.9) にこの電流密度ベクトル場 ie(r′) を代入して、 ϵ が十分小さいとき x′= y′ = 0 の近傍でしか値を持たな いことを使うと、 B(r) = µ0 4π ˚ ie(r′)× (r − r′) |r − r′|3 d 3r′ ≈µ0I 4π2 ˚ ϵ2 (x′2+ y′2+ ϵ2)2 ·k× (xi + yj + (z − z′)k) [x2+ y2+ (z− z′)2]32 dx′dy′dz′ =µ0I 4π2(−yi + xj) ˆ dz′ [x2+ y2+ (z− z′)2]32 · ¨ ϵ2 (x′2+ y′2+ ϵ2)2dx ′dy′ =µ0I 4π (−yi + xj) ˆ ∞ −∞ dz′ [x2+ y2+ (z− z′)2]32 =µ0I 4π (−yi + xj) ˆ ∞ −∞ dz′ [ x2+ y2+ z′2]32 = µ0I 2π(x2+ y2)(−yi + xj) (8.12) を得る。これは以前に得た結果である。 式 (8.9) で与えられる磁場 B(r) に対して、回転を計算 しよう。そのために、 ˚ ie(r′)× (r − r′) |r − r′|3 d 3r′ =∇ × ˚ ie(r′) |r − r′|d3r′ (8.13) と書くことができることを確かめよう。実際、右辺の x 成 分は ∂ ∂y ˚ [ie(r′)]z |r − r′|d3r′− ∂ ∂z ˚ [ie(r′)]y |r − r′|d3r′ = ˚ [ie(r′)]z ∂ ∂y 1 |r − r′|d3r′ − ˚ [ie(r′)]y ∂ ∂z 1 |r − r′|d 3 r′ = ˚ [ie(r′)]z−(y − y ′) |r − r′|3 d 3r′ − ˚ [ie(r′)]y−(z − z ′) |r − r′|3 d 3r′ = ˚ [ie(r′)]y(z− z′)− [ie(r′)]z(y− y′) |r − r′|3 d 3r′ (8.14) となって、左辺の x 成分に等しいことが示せる。y 成分、 z 成分についても同様。 以上から、 B(r) =∇ × [ µ0 4π ˚ ie(r′) |r − r′|d3r′ ] (8.15) であることがわかる。 公式 ∇ × (∇ × X) = ∇(∇ · X) − ∇2X (8.16) を用いると8、 ∇ × B(r) = ∇ (∇ · X(r)) − ∇2X(r) (8.17) と表せる。ただし、ここで X(r) = µ0 4π ˚ ie(r′) |r − r′|d3r′ (8.18) を導入した。ここで ∇2=∇ · ∇ = ∂2 ∂x2 + ∂2 ∂y2 + ∂2 ∂z2 (8.19) はラプラシアンと呼ばれる。 r′ についての微分を∇′ で表すと、 ∇ 1 |r − r′| =−∇′ 1 |r − r′| (8.20) であるから ∇ · X(r) = µ0 4π ˚ ie(r′)· ∇ 1 |r − r′|d3r′ =−µ0 4π ˚ ie(r′)· ∇′ 1 |r − r′|d3r′ =−µ0 4π ˚ (∇′· ie(r′)) 1 |r − r′|d 3r′ (8.21) 8ベクトル 3 重積の公式 (教科書 p.8) を参照。今の場合、∇ は微分演 算子で X と交換しないことを考慮しなくてはならない。
を得る。最後のステップで部分積分を用いた。ここで、定 常的な電流密度ベクトルに対して ∇ · ie(r) = 0 (8.22) が電荷の保存則から成り立つ。(発散が「湧き出し」を表し ていたことを思い出そう。電荷はどこからも「湧き出し」 たりはしない。) それゆえ、∇ · X(r) = 0 である。 ∇X(r) を計算するにあたって、1/|r − r′| の r = r′ で の振舞いが悪いので、前と同様に微小な正数 ϵ を導入して X(r) を X(r) = µ0 4π ˚ ie(r′) √ |r − r′|2+ ϵ2d 3r′ (8.23) と表そう。 ∂ ∂x 1 √ |r − r′|2+ ϵ2 = −(x − x′) [|r − r′|2+ ϵ2]32 (8.24) ∂2 ∂x2 1 √ |r − r′|2+ ϵ2 = −1 [|r − r′|2+ ϵ2]32 + 3 (x− x ′)2 [|r − r′|2+ ϵ2]52 (8.25) などから ∇2√ 1 |r − r′|2+ ϵ2 = −3ϵ2 [|r − r′|2+ ϵ2]52 (8.26) この関数には以前にも式 (7.6) で出会っている。 ∇ × B(r) = −∇2 X(r) = µ0 4π ˚ ie(r′) 3ϵ 2 [|r − r′|2+ ϵ2]52 d3r′ ≈ µ0 4πie(r) ˚ 3ϵ2 [|r − r′|2+ ϵ2]52 d3r′ = µ0ie(r) (8.27) を得る。すなわち、 ∇ × B(r) = µ0ie(r) (8.28) である。この式は電場に対する式 (7.11) に対応する式で、 (微分形での) アンペールの法則と呼ばれる。(各点におけ る) 電流密度が (その点での) 磁場の回転を与えるというこ との数学的表現である。