Computing Phylogenetic Roots with Bounded Degrees and Errors is Hard (Evolutionary Advancement in Fundamental Theories of Computer Science)

42

Computing Phylogenetic Roots with Bounded Degrees and

Errors

is

Hard

Tsukiji

Tatsuie1

and Zhi-Zhong

Chen2

1 _{築地 立家}

DepartmentofInformation Science, TokyoDenki University, Hatoyama, Saitama 350-0394, Japan.

$\mathrm{t}$sukiji@j .dendai. $\mathrm{a}\mathrm{c}.\mathrm{j}\mathrm{p}$

2 _隙致中

DepartmentofMathematical Sciences,Tokyo Denki University, Hatoyama, Saitama 350-0394,

Japan. chenQr.dendai

.

$\mathrm{a}\mathrm{c}.\mathrm{j}\mathrm{p}$

Abstract. The $\mathrm{D}\mathrm{E}\mathrm{G}\mathrm{R}\mathrm{E}\mathrm{E}-\Delta$ CLOSEST PHYLOGENETIC $k\mathrm{T}\mathrm{H}$ Root PROBLEM $(\Delta \mathrm{C}\mathrm{P}\mathrm{R}k)$ is the problem of finding a (phylogenetic) tree $T$ from a given graph $G=(V, E)$ such that (1) the

degreeofeachinternal node of$T$isat least 3 andat most$\Delta$,(2)theexternalnodes($i.e$

.

leaves)

of$T$areexactlytheelementsof$V$,(3)The number of disagreements, $|E\mathrm{a}$

{

$(u, v)$ :$u$,$v$areleaves

of$T$ and$dr(u, v)\leq k\}|$ does notexceed a given number, where$d_{T}$(u,$v$) denotes the distance

between $u$ and $v$ in tree $T$

.

We show that this problem is $\mathrm{N}\mathrm{P}$-hard for every fixed constants

6,$k\geq 3.$

Our majortechnical contribution is the determination of all pylogenetic roots that approximate the almost largest cliques. In more precise, let $f_{\Delta}(k)$ be the size of alargest clique having a

$k\mathrm{t}\mathrm{h}$phylogenetic rootwithmaximumdegree$\Delta$

.

We determinetheall phylogenic$k\mathrm{t}\mathrm{h}$rootswith

maximumdegree4 that approximate the$(f_{\Delta}(k)-1)$-cliquewithinerror2, whereweallowthe

internal nodes ofphylogenyto have degree 2.

1

Introduction

A

phylogeny is

a

tree where the leaves

are

labeled by species and each internal node represents

a

speciation event whereby

an

ancestral species gives rise to two

or

more

child species. The internal

nodes of

a

phylogeny have degrees (in the

sense

ofunrooted trees, $i$

.

$e$

.

thenumber of incident edges)

at least

3.

Specifically, interspecies similarity is represented by

a

graph where the vertices

are

the

species and the adjacency relation representsevidence of evolutionary similarity.

A

phylogenyis then

reconstructed from the graph such that the leaves of the phylogeny

are

labeled by vertices of the

graph ($i.e$. species) and for anytwo vertices ofthe graph, they

are

adjacent in the graph if andonly

iftheir corresponding leaves inthe phylogeny

are

connected by

a

pathoflengthatmost $k$, where $k$is

a

predeterminedproximitythreshold. To beclear, vertices in the graph

are

called vertices while those

inthe phylogeny nodes. Recall that the length ofthe (unique) path connecting two nodes $u$ and$v$

in

phylogeny $T$is the number of edges

on

the path, which is denoted by $d_{T}(u, v)$

.

This approach gives

rise to the followingalgorithmicproblem [5]:

PHYLOGENETIC $k\mathrm{T}\mathrm{H}$ Root PROBLEM (PRfc):

Given

a

graph $G=(V, E)$, find

a

phylogeny $T$ with leaves labeled by the

elementsof$V$ such that foreach pairofvertices $u$,$v\in V$, $(u, v)\in E$if and

onlyif$d_{T}(u,v)\leq k.$ 数理解析研究所講究録 1375 巻 2004 年 42-48

43

Such

a

phylogeny$T$ (if exists) iscalled

a

phylogenetic$k\mathrm{t}\mathrm{h}$root,

or a

$k\mathrm{t}\mathrm{h}$rootphylogeny, ofgraph$G$

.

Graph $G$ is called the$k\mathrm{t}\mathrm{h}$ phylogeneticpowerof$T$

.

For convenience,

we

denote the $k$th phylogenetic

power of

a

phylogeny $T$

as

7$k$$(T)$

.

That is, Vu(T) has the vertex set $L(T)=\{u$ : $u$

are

leaves of

$T$

$\}$ and the edge set $T^{k}=$

{

$(u$,$v$) $|u$ and $v$

are

leaves of$T$ and $d_{T}(u,$$v)\leq k$

}.

Thus, $\mathrm{P}\mathrm{R}k$ asks for

a

phylogeny$T$ such that _{$G=P_{k}(T)$}

.

The input graphin$\mathrm{P}\mathrm{R}k$ is derived from

some

similarity data, whichis usuallyinexact in practice

and may have

erroneous

(spurious

or

missing) edges.

Such

errors

may

result in graphs that have

no

phylogenetic roots and hence

we are

interested in finding approximate phylogenetic roots for such

graphs. For

a

graph $G=(V, E)$, each tree $T$ whoseleaves

are

exactly theelements of$V$ iscalled

an

approximatephylogeny of$G$, and the

error

of$T$ is $|7$

$k$

ea

$E|=|$$(E-T^{k})\cup(T^{k}-E)|$

.

This motivated

Chen et.

at.

to consider thefollowing problem:

CLOSEST PHYLOGENETIC $k\mathrm{T}\mathrm{H}$ Root PROBLEM (CPRfc):

Given

a

graph $G=(V, E)$ and

a

nonnegative integer $\ell$, decide if$G$ has

an

approximate phylogeny$T$with at most $\ell$

errors.

An approximate phylogeny of $G$ with the minimum

errors

is called

a

closest $k\mathrm{t}\mathrm{h}$ root phylogeny of

graph $G$

.

The hardness of PRCforlarge$k$

seems

to

come

fromtheunbounded degreeof

an

internal nodein

the output phylogeny.Ontheotherhand,in the practice ofphylogenyreconstruction,mostphylogenies

considered

are

trees of degree 3 [7] because speciation events

are

usually bifurcating

events

in the

evolutionaryprocess. We call these restricted

versions

the$\mathrm{D}\mathrm{E}\mathrm{G}\mathrm{R}\mathrm{E}\mathrm{E}-\Delta$$\mathrm{P}\mathrm{R}k$

and

the$\mathrm{D}\mathrm{E}\mathrm{G}\mathrm{R}\mathrm{E}\mathrm{E}-\Delta$CPRk,

and denotethem for short

as

$4\mathrm{P}\mathrm{R}7\mathrm{c}$and ACPRk, respectively.

1.1 Previous Results

on

Phylogenetic Root Problems

$\mathrm{P}\mathrm{R}k$

was

first studied in [5] wherelinear-timealgorithms for PR2 andPR3

were

proposed. A

linear-time algorithm for the special

case

of PR4 where the input graph is required to be connected,

was

also presented in [5]. At present, the complexity of$\mathrm{P}\mathrm{R}k$with _{$k\geq 5$} is stillunknown.

Chen et. al. [2] presented

a

linear-time algorithm that determines, for any input connectedgraph

$G$ and constant $\Delta$ _{$\geq 3,$} if$G$ has

a

$k\mathrm{t}\mathrm{h}$root phylogeny with degree at most

$\mathrm{a}$, and if so, demonstrates

one

such phylogeny. Onthe other hand, Chen et. al. [2] showedthat CPRk is $\mathrm{N}\mathrm{P}$-complete, for any

$k\geq 2.$ One of theiropen questions asks for the complexity of$\Delta$CPRk.

Ofspecial interest is CPR2. CPR2 is essentially identical to the correlation clustering problem

which has drawn much attention recently [1], The proofof the $\mathrm{N}\mathrm{P}$-hardness of CPR2 given in [2] is

also

a

valid

proof

of

the$\mathrm{N}\mathrm{P}$-hardness

of the

correlation Clustering problem.

1.2 Our Contribution

In this

paper,

we

will show that ACPRkis $\mathrm{N}\mathrm{P}$-complete, forevery $k\geq 3$ and

IS

$\geq 3.$ This

answers

an

open question in [2].

In

a

course

of the proof

we

first reduce HAMILTONIAN PATH,

a

famous $\mathrm{N}\mathrm{P}$-complete problem, to

$4\mathrm{C}\mathrm{P}\mathrm{R}3$, and then ACPRSto ACPRk. Theformerreduction is tedious but

a

routinework.

On

the

other ha $\mathrm{d}$, the latter reduction

seems

to require

new combinatorial

investigation that is proper of

$\Delta$

CPRk.

44

-There is

a

tree$T$ of maximum degree

4

whose phylogenetic $k\mathrm{t}\mathrm{h}$power is $G$and such that $T$ has

a

uniqueunsaturated ($i.e$

.

degree $<4$) internal node $\alpha$

,

the degree ofat is

a

– 1, $\mathrm{d}\mathrm{r}(\mathrm{a}, u)$ $=h$

holds for

one

leaf$u$ and $d_{T}(\alpha,v)\geq h+1$ for all leaves $v$otherthan $u$.

-For everyapproximate phylogeny$T$of$G$ with maximum degree$\Delta$ and at most $\ell$errors, there is

at most

one

pair $(\alpha,u)$ such that $\alpha$ is

an

unsaturated internal node of$T$

,

$u$ is

a

leaf of$T$, and

$\mathrm{d}\mathrm{r}(\mathrm{a}, u)$ $\leq h;$ moreover, if$(\alpha,u)$ existsthen the degreeof$\alpha$ in $T$is

5-1.

Then,

_we

establish the reduction from ACPRZ to$\Delta \mathrm{C}\mathrm{P}\mathrm{R}k$byproviding

a

family of$(\Delta$

,

$k$, $\lfloor k/2\rfloor-$

$1$,2)-core

graphs

for every fixed

_{$4\geq 3$}

and

_{$k\geq 4.$}

Our construction of a

(A $k,\cdot\lfloor k/2\rfloor-1,2$)

more

graph

is

a

pile of $(\mathrm{A}, k’, 1,2)$

-core

graphs for $k’=5,7$

,

$\ldots$

,

$k$ if$k\geq 5$ is odd, and $k’=4,6$

,

$\ldots$

,

$k$ if$k\geq 4$

is

even.

So,

a

more

basicproblem is to

prove

that

a

certaingraph is

a

$(\mathrm{A}, k, 1,2)$

-core

graph.

The maximum size of

a

clique having

a

(nO-error) $k\mathrm{t}\mathrm{h}$root phylogeny with

maximum

degree

4

is

givenby the followingfunction,

$f_{\Delta}(k)=\{$

$\Delta\cdot(\Delta-1)9-1$,if$k$ is even,

2

.

(4-1)$k\mathrm{T}^{1}$

, if$k$ is odd.

We prove that the clique of size $f_{\Delta}(k)-1$ is

a

$(\Delta, k, 1,2)$

-core

graph. Moreover,

we

determine the

all $k\mathrm{t}\mathrm{h}$root phylogenies with maximum degree

a

that approximate the clique within

error

2, where

we

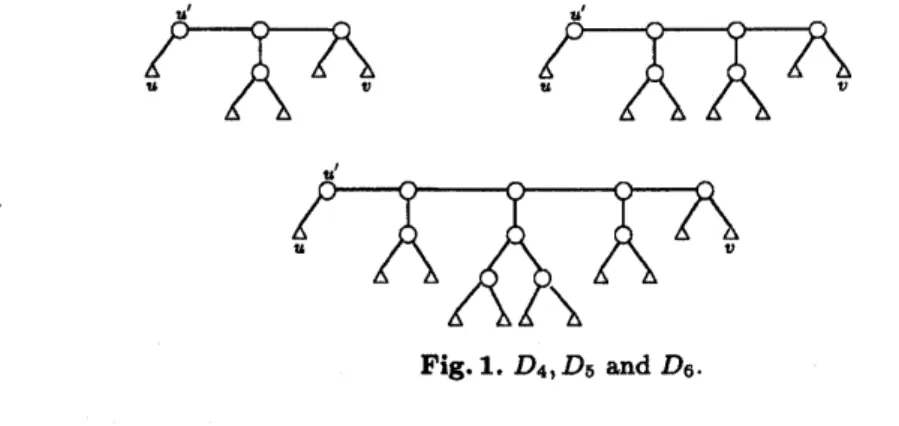
allow theinternal nodes ofphylogeny tohave degree 2. Forexample, all phylogeneticroots ofthe

$(f_{3}(5)-1)$ clique

are

$D_{5}$ in Figure 1, $E_{5}$ inFigure 2, and the tree obtained from$D_{5}$ by removingthe

leaf$u$

.

2

Notations and

Definitions

We employ standard terminologies in graph theory. In particular, for

a

graph $G$, _$V(G)$ and _$E(G)$

denote the sets of vertices and edges of $G$, respectively. An induced subgraph of

a

graph $G$ is the subgraph $H$ induced by

a

subset $W$ of $V(G)$

,

$i.e$

.

$\mathrm{E}(\mathrm{H})=$

{

$(\mathrm{u},\mathrm{v})$

:

$u,v\in W$ and $(\mathrm{w},\mathrm{v})\in E(G)$

}.

Two graphs $G=(V, E)$ and$G’=(V’, E’)$

are

isomorphicif there is

a

one-tO-One correspondence $\phi$

between $V$ and$V’$ such that $(u, v)\in E$ if and only if$(\phi(u), \mathrm{O}(\mathrm{v}))\in E’$, and

we

denoteit

as

$G\cong_{\phi}G’$

.

The distance between twovertices$u$and $v$in $G$is denotedby $d_{G}(u,v)$

.

The degree of

a

vertex$v$in $G$

is denotedby da(v), which isthe number of vertices adjacent to$v$ in$G$

.

Similarly, for

a

tree$T_{:}V(T)$,

$E(T)$

,

and $L(T)$ denote the setsofnodes, edgesand leavesof$T$, respectively.

We alsointroduce

some new

terminologies oftrees for

convenience.

For

a

tree$T$ofmaximumdegree

$\Delta$,

an

internalnode

$\alpha$of$T$isunsaturatedif$d_{T}(\alpha)\leq$A-l. Tree$T$is$i$-extensibleif$i= \sum_{v}(\Delta-deg_{T}(v))$,

where the summation is taken

over

all unsaturated internal nodes $v$ of$T$

.

A tree $T$ is $h$-away if for each unsaturatedinternal node$x$of$T$

,

the

minimum

distance

from

$x$to

a

leaf is at least $h$and

further

there is exactly

one

leaf$v_{l}$ such that $d_{T}(x,v_{li})=h.$ For any set $U$ of nodes of$T$, $\mathrm{T}[\mathrm{J}7]$ denotes the

minimum subtree containing$U$. Note that each leaf of_$T[U]$ belongs to $U$

.

A phylogeny is atreethat

contains

no

degree2nodes.

As

already mentioned,the$k\mathrm{t}\mathrm{h}$phylogeneticpowerofany tree$T$isdenoted

as

Vk(T) $=(L(T),T^{k})$, $T^{k}$ is the set of edges _{$(u, v)$} with _{$\{u,v\}\subseteq L(T)$} and_{$d_{T}(u, v)\leq k.$}

3

Construction

of

$(\Delta, k, \lfloor k/2\rfloor ・1, 2)$

-core

graphs

In this section

we

give

a

construction

of (3,$k$,$\lfloor$7c/2$\rfloor$ – 1,2)-core graphs for every odd _{$k\geq 5.$} It is

straightforward to generalize the arguments of this sectionto obtain $(\Delta, k, \lfloor k/2\rfloor ・1, 2)$

-core

graphs

45

Throughout thissection, alltreesand phylogenies

are

ofmaximum degree

3 or

less. Weabbreviate

$\mathrm{f}\mathrm{s}(\mathrm{k})$

as

$\mathrm{f}(\mathrm{k})$

.

The proofs of themost lemmas and corollaries

are

omitted due to lack of space.

A

phylogenywhose$k\mathrm{t}\mathrm{h}$phylogenetic power realizes the $f(k)$-clique

can

be

constructed

as

follows:

Start

with

a

path $P$ of length exactly $k$

.

Let $u$ and $v$ be the endpoints of$P$

.

Then connect

as

many

new

nodes

as

possible

so

that $P$ becomes

a

tree of degree 3 and every node has distance at most $k$

ffom both$u$ and $v$

.

Thistree is unique up toisomorphism and hence

we

denote it by $C_{k}$

.

Moreover,

removing

an

arbitraryleaf from$C_{k}$ yields

a

tree, which is unique up toisomorphism.We denote this

tree by$D_{k}$

.

Figure 1 depicts$D_{4}$

,

$D_{5}$, and$D_{6}$ where themissingsiblingleaf ofti hasbeen removed. By

definition, the $k\mathrm{t}\mathrm{h}$phylogenetic powerof_{$D_{k}$} is

an

$f(k)-1$ clique.

Fig.1.$D_{4}$,$D_{6}$ and$D_{6}$

.

Lemma 1. Forevery tree$T$ (of maimum degree 3),

if

there are two leaves$u$ and$v$ with$d_{T}$(u,$v$) $=k$

and allleaves$w$

of

$T$ have distance at most$k$

from

both _$u$ and$v$, then $T$ is isomorphic to

a

subtree

of

$C_{k}$

.

Corollary 1. Forany tree$T$,

if

$dr\{u,$$v$) $\leq k$

for

all leaves$u$ and$v$, then$T$ is isomorphic toa subtree

of

$c_{k}$

.

FVict 1 For every tree$T$ with _{$|L(T)|=f(k)$}-1 and $|Tk|\geq(_{2}^{f(k)-1})-2,$

we

have$d_{T}(u,v)\leq k$

for

all

but at

most teuo

unorderedpairs $(u,v)$

of

leaves

of

$T$

.

Lemma 2. Let$k\geq 4.$ Let$T$ be

an

arbitrary tree such that_$|L(T)$$|=f(k)-1$ and$|Tk|\geq(_{2}^{f(k)-1})-2.$

Then, there

are

leaves$u$ and$v$

of

$T$ with$d_{T}(u,v)=k.$

Lemma 3. Let$k\geq 6.$ Let$T$ be

an

arbitrary treehaving$f(k)-1$ leaves. Suppose that there areleaves

$u$

,

$v$,$w$

of

$T$ such that_{$d_{T}(u, v)=k$} and_{$\max(d_{T}(u, w),$$dr\{u,$}$w$)) $\geq kf$$1$

.

Then, $|T^{k}|\leq(_{2}^{f(k)-1})-3.$

Lemma 4. Let$k\geq 6.$ Let$T$ be

a

treehaving $f(k)-1$ leaves such that $|\mathrm{r}k|\geq(_{2}^{f(k)-1})$ - 2. Then$T$

is 0-extensible

or

1-extensible. Moreover,

if

$T$ is 1-extensible then$T\underline{\simeq}D_{k}$

.

For $k\in\{4,5\}$

,

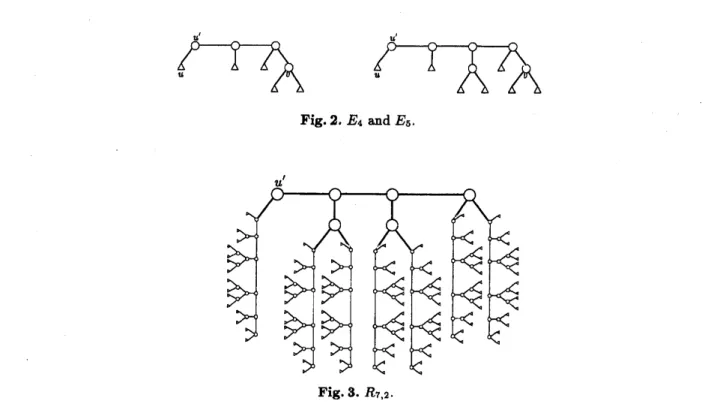
let$E_{k}$ bethetree inFigure 2.

Lemma

5.

Let$k\in\{4,5\}$

.

Let

$T$ be

a

tree

having_$f(k)$ $-1$ leaves such that $|Tk|\geq(_{2}^{f(k)-1})-2.$ Then

48

Fig.2. $E_{4}$ and$E_{6}$

.

Fig.$\theta$

.

$R_{7,2}$

Theorem 1. Forevery$k\geq 4,$ the $(f(k)-1)$ -clique is _{$a(3, k, 1,2)$}

-core

graph.

Now

we are

readytoconstruct

a

$(3, k, \lfloor \mathrm{A}/2\rfloor-1, 2)$

-core

graphfor every odd$k\geq 5.$ Werecursively

constructtrees$R_{k,\lfloor k/2\rfloor-1}$, $k=5,7,9$,$\ldots$, anddefine

a

family of$(3, k, \lfloor k/2\rfloor- 1, 2)$

-core

graphs

as

the

kthphylogenetic power of thetrees $R_{k,\lfloor k/2\rfloor-1}$ (seeFigure

3

for$R_{7,2}$ ):

-Let $h_{k}=\lfloor k/2\rfloor-$$1$

.

For each $1\leq i\leq h_{k}$

,

let_{$g(i)= \prod_{j=1}^{t}(f(2j+3)-1)$}

.

Let _$g(0)=1.$

$-\tilde{R}_{k,h_{k}}$ is

a

leveled tree of depth $h_{k}$ such that at depth _{$i(0\leq i\leq h_{k})$}

are

placed _$g(i)$ nodes and

each node $v$ at depth$i<h_{k}$ is connected to

some

$f(2i+5)-1$ nodesat depth _$i+$ l.

$-R_{k,h_{k}}$ is

an

expansion of$\tilde{R}_{k,h_{k}}$ such that each node _$v$ of $\tilde{R}_{k,h_{k}}$ at depth $i$ $(0\leq i\leq h_{k}-1)$ is

expandedto

a

copy $D(v)$ of$D_{2:+5}$ in $R_{k,h_{k}}$, where $v$ isidentified with the degree-2node of$D(v)$

and thechild nodes of$v$ in $\tilde{R}_{k,h_{k}}$

are

identified with the leaves of

$\mathrm{D}(\mathrm{v})$ in

an

arbitraryonetoone

manner.

By construction, $R_{k,h_{h}}$ is 1-extensible and $h_{k}$-away, and has

a

unique degree-2 node, namely, the

unique degree-2 nodeof$D_{5}$

.

Lemma 6. Let$k\geq 4.$ Let$T$ be

a

tree having$f(k)-1$ leaves such that$|T_{k}|$ $\geq(_{2}^{f(k)-1})-2.$ Suppose

further

that$T$ isnot0-extensible. Let_$T(w)$ bethetree obtainedby connectinga

neen

leaf

to an arbitrary

leaf

$w$

of

T. Then, $|\mathrm{T}(\mathrm{w})|^{k}\leq(_{2}^{f(k)-1})-3.$

Lemma

7.

Let$k\geq 5$ beodd. Let$T$ be

a tree

such that$L$(7 ) $=$L(Rk,hk) and$|Tk$$\oplus R_{k,h_{k}}^{k}|\leq 2.$ Then, $T$ is 0-extensible

or

1-extensible. Moreover,

47

Theorem 2. Forevery odd$k\geq 5,$ the graph$7^{\mathit{2}_{k}}(R_{k,\lfloor k/2\rfloor-1})$is $a$ $(3, k, \lfloor k/2\rfloor-1, 2)$

-core

graph.

Theseconstructions, lemmas and theorems

can

be generalized to every fixed$k\geq 4$ and $\Delta\geq 3.$ A

phylogenic $k\mathrm{t}\mathrm{h}$root of the _{$f_{\Delta}(k)$}-clique

can

be constructed in the

same

way

as

$D_{i}$ and

we

denote it

as

$Ds,i$

.

We

can

construct

a

phylogeny$R_{\Delta,k,h_{k}}$ of degree $\Delta$ recursivelyin the

same

way

as

$R_{k,h_{k}}$ but replacing$f$ and $D_{i}$ therein with $f_{\Delta}$ and $D_{\Delta,i}$, respectively; further, if$k$ is

even

then thefunction_$g(i)$ thereinshould be replaced by $\prod_{j=1}^{i}(f_{\Delta}(2j+2)-1)$

.

Lemma

7

and Theorem 2

can

be generalized

as

follows:

Lemma 8. Let$k\geq 4$ and

a

$\geq 3.$ Let$T$ be

a

tree

of

mairnurn degree$\Delta$ such that_{$L(T)=L(R_{\Delta,k,h_{k}})$}

and$|Tk\oplus R_{\Delta,k,h_{k}}^{k}|\leq 2.$ Then$T$ is $\theta$-extensible

or

1-extensible. Moreover,

if

$T$ is 1-extensible then it

is $h_{k}$-away.

Theorem 3. For every$k$

a

4,

$\mathcal{P}_{k}(R_{\Delta,k,\lfloor}c\mathit{7}2\rfloor-1)$ is $a(\Delta,$$k$

,

$\lfloor k/2\rfloor-$ $1$,$2i$

-core

graph.

4

The

$\mathrm{N}\mathrm{P}$

-hardness of

$\Delta$

CPRk

This section proves that 3CPR& is $\mathrm{N}\mathrm{P}$-hard for each odd _{$k\geq 3.$} It is straightforward to generalize

thearguments ofthis section to prove that $3\mathrm{C}\mathrm{P}\mathrm{R}k$ is $\mathrm{N}\mathrm{P}$-hardforforevery _{$4\geq 3$} and

$k\geq 3.$

Throughoutthis section, alltreesandphylogenies

are

of maximumdegree3

or

less. Proofsof most lemmas andcorollaries

are

omitted due to lackof space.

We begin with the $\mathrm{N}\mathrm{P}$-hardness proofof$3\mathrm{C}\mathrm{P}\mathrm{R}3$because the $\mathrm{N}\mathrm{P}$-hardness proofs of$3\mathrm{C}\mathrm{P}\mathrm{R}\mathrm{A}$; for largerodd$k$ arereductionsfromit.Wereduce the following version ofHAMILTONIAN PATH PROBLEM

(HP) to $3\mathrm{C}\mathrm{P}\mathrm{R}3$, whose $\mathrm{N}\mathrm{P}$-hardnessproofs

can

be foundin [3] and [6, Section 9.3].

HAMILTONIAN PATH PROBLEM (HP): Given agraph $G=(V, E)$ such that

- all vertices

are

of degree3

or

less,

- twospecificvertices

are

of degree 1 and each ofthemis adjacent to

a

vertex of degree 2, and

- thereis

no

cycle of length less than

5.

Find

a

Hamiltonian

pathof$G$, $i.e$

.

find

a

linearordering of the vertices of$G$ such that each pair

of consecutive vertices

are

adjacent in $G$

.

Let $G=(V, E)$ be

an

arbitrary instance of $\mathrm{H}\mathrm{P}$, hence the maximum degree of _$G$ is 3 and _$G$

contains

no

cycle oflength less than 5. Let $T=(V, E(T))$ be

an

approximate phylogeny of $G$

.

We

define

a

fractionalvalue$cost_{\mathit{3}}(v)$ associated with each vertex$v\in V$

as

follows:

COSt3

$(v)= \frac{1}{2}|$

{

$u$ : $(u,v)\in E$and$d_{T}(u,$$v)>3$

}

$|$

$+|$

{(

$u$,$w$) : $u\neq w$,$(u,$$v)\in E$,$(v,$$w)\in E$, $(u,$ $w)$

\not\in

$E$and$d_{T}(u,$$w)\leq 3$

}

$|$

.

Lemma 9. The

surn

_of

$cost_{\mathit{3}}(v)$ overall vertices $v\in V$ is no

more

than $|7$$3\oplus E|$

.

Lemma

10. Let

$v$ be

a vertex

of

$G$ having threepairwise nonadjacent neighbors$u_{1},u_{2}$ and113. Then,

COSt3

$(v)= \frac{1}{2}$

or

cOst3$(v)\geq 1.$ Moreover,

if

$cost_{\mathit{3}}(v)$ $= \frac{1}{2}$, then$d_{T}(u_{i}, v)>3$

for

one

$u_{\dot{*}}\in\{u_{1},u_{2},u_{3}\}$

and$d_{T}(u_{j}, v)=3$

for

the other

two

$u_{j}\in\{u_{1},u_{2},u_{3}\}-$$(u_{\mathrm{i}}\}$.

48

Theorem

5. For

every

odd$k\geq 3,$

3CPR&

is NP-complete.

It is straightforward togeneralize Theorem 5 to every $4\geq 3$ and $k\geq 4,$ obtaining thefollowing

theorem.

Theorem 6. For

every

$\Delta\geq 3$ and every$k\geq 3,$ 3CPR& is NP-complete.

5

Summary

and

an

Open Question

Wehave provedthat

ACPRk

is$\mathrm{N}\mathrm{P}$-completefor every $\mathrm{i}$ _{$\geq 3$}and

$k\geq 3.$

A

more

fundamental

problem

is the TREE $k\mathrm{T}\mathrm{H}$ Root PROBLEM $(\mathrm{T}\mathrm{R}/\mathrm{c})$

,

where the nodes (not only the leaves) of$T$ correspond

to the vertices of $G$

.

Kearney and Corneil proved that CTRA; is $\mathrm{N}\mathrm{P}$-complete when $k\geq 3[4]$

.

We

conjecturethat $4\mathrm{C}\mathrm{T}\mathrm{R}k$is $\mathrm{N}\mathrm{P}$-completefor

every

fixed _{$4\geq 3$} and _{$k\geq 2.$}

References

1. N. BANSAL, A. BLUIVI, AND S. CHAWLA, Correlation Clustering, in Proceedings of the $43\mathrm{r}\mathrm{d}$ Symposium

on Foundations ofComputer Science (FOCS 2002), pages 238-250, 2002.

2. Z.-Z. CHEN, T. JIANG, AND G.-H. LIN, Computing phylogenetic roots with bounded degrees and errors, SIAM Journalon Computing,toappear. A preliminary versionappearedin Proceedings ofWADS2001.

3. M. R. GAREY, D. S. JOHNSON AND R. E. TARJAN, The Planar Hamiltonian Circuit Problem is

$NP$-Complete,SIAMJournalon Computing, _{$5(4):704-714$}, 1976.

4. P. E. KEARNEYAND D. G. CORNEIL, $\mathrm{R}ee$powers, Journal of Algorithms, 29:111-131, 1998.

5. G.-H. Lin, P. E. KEARNEY, AND T. JIANG, Phylogenetic $k$-root and Steiner$k$-rvot,in The 11thAnnual

International SymposiumonAlgorithms and Computation (ISAAC 2000), volume 1969 of Lecture Notes inComputer Science, pages539-551, Springer, 2000.

6. C. H. PAPADJMITRIOU, Computatational Compleity,Addison-Wesley, 1994.

7. D. L. SWOFFORD, G. J. OLSEN, P. J. WADDELL, AND D. M. HILLIS, Phylogenetic inference,In D. M. Hillis, C. Moritz, and B. K. Mable, editors, MolecularSystematics (2nd Edition), pages407-514, Sinauer