The frequency characteristics of the ripple by which the temperature is accompanied was also discussed.

1

On the Electron ~nergy In an Ar~ernat:ing Field

Mitsugu KONOMI Summary : The purpose of present study is to discuss the frequency characteristics of the energy of electrons in a gas when an alternating electric field is impressed. The basic equation was derived on the assumption that the distribution of electron energy is Maxwellian, collision between electrons and molecules is elastic and the mean free path of electron is independent of its energy.

The transient response of the electron temperature to a stepwise variation of the field was treated of. and the results were shown in figures. Taking electrons in helium as an example. the progress of the variation of the temperature immediately after the impression of the field was numerically computed to get a general idea of the transient response to an a.c. field.

The frequency characteristics of the ripple by which the temperature is accompanied was also discussed.

An additional remark was given on the pulsation of electron density in a luminous column of h. f. glow where the ambipolar diffusion is the sole mechanism of disappearance of electrons.

Int:roduct:i

⁰

n

Mobility. coefficient of diffusion, number of ionization by collision. etc. which play an important role in electrical discharge phenomena cannot be treated of without a thorough information about the energy of electrons in the electric field.

(I)

In connection with his theory on electrodeless discharge. Townsend gave a brief account of the electron energy in h. f. field.

m

Yamamoto and Nobata gave an approximate Solution for the waveform of the electron energy in a sinusoidal field.

(3)(4)

The author also tried to get the waveform of electron temperature, but his result was valid only for the case where the the frequency of the field is sufficiently low. So, it requires a further study to get a more general idea on the electron energy in an a .c, field.

Basic Fquation

In an electric field an elelectron in a gas advances in the field until it comes into collision with a gas molecule, meanwhile acquiring energy from the field, and gives a certain fraction of its energy to a molecule which is subjected to collision. Thus a number of electrons repeat gaining and losing energy alternately. and, as a result. they continually convert the energy gained from the field into the energy of random motion. The energy of the random motion might be diverse widely for an individual electron, and. if the distribution follows Maxwell's low. a concept of electron temperature arises.

As other authors have hitherto done, we hereafter assume that the distridution of electron energy is Maxwellian.

When an electron collides with a gas molecule after abvancing in the field. the direction of

the velocity that the electron has immediately after the collision might be spontaneous. So,

when a large number of electrons is taken into account, it may be regarded that an electron statistically loses its velocity by collision with a molecule, or in other words. an electron stt r ..s for a new free travel without any initial velocity.

53, the velocity that an electron pocesses after a free time r is

V = e S t ^{€(t)dt V =0 at t-r. . (1)}

m t-r

where e is the charge of an electron. m its mass and e(t) the intensity of the electric field.

If r is the mean free time. the probability with which free time lies between rand r + dr is exp(-r!r') dr/;.

We shall consider a crowd of electrons each of which collides with gas molecules many times in an unit time. Let s be the number of electrons, Vn the number of collisions of the electron per unit time, tnp the time at which the pth collision occurs anb Vnp the free time betweentp-r-Dth and pth collisions of this electron. So

),I.

::E 't"np = 1 and

~-1

· .. ···· .. · .. · .... ··· .. · .. ···(2)

•.. ·• ... ··· .. ·•··· .. ·· .. •••••···•·•···· .. (4) Then the energy gained by an electron per unit time averaged over the free time is

') I

lJ. SO 'l"np stnD

Wg=~c-.~::E e--~-- { e(t)dt}2drnp .. ··· .. · .... ·.. ··· .... ··· .... ···(3)

Zsm. ·~l

^1'-1 _-,",

t

_ntJ

--r _np

When a number of colllisions occurs between an electron and molecules while the intensity of the field varies little, whole electrons might come into collisions almost simultaneously

^J

8) t l P =t2P = ... = t p holds in (3)

2

v. SO ^t'p st ^p

w« =2 e -L e---;- { e ro dt}2drp

m'~·l _,", ^tnp-t'np

If the field varies so slow that t p in (4) can be regarded constant.

e

²

SO --:p- st ')

Wg = _-2m~ 2 e: r { e (t) dt} -dt" ·(5)

-00

t p -t'p

or, to a further approximation, we have

··•···· .... ·• .. ·· ... •· .. · .. ···· .. •··· .. · .. · .. (6)

.. •.. • .... •··••· .. ·•·• .... · .. ···•• .. ···· .... ·• .. •.. (7) According to what has been known for the d. c. field, the electron mobility is given by

b=0.75~

m

So the rate of energy gain from the field of intensity Eo is ^Wll =0. 75e2~Eo2 [m,

On the basis of this fact, it may be reasonable to adopt the following expression instead of (6),

· .. · .. · .... ···· .. ···· .... ·•· .... •· .. · .. ··· .. ·· .... ·(8)

If e(t) is a periodic function of time and the variation of the field is not small in the mean

free time" the time at which collision occurs is diverse and as a result. the rate of gain of

energy tends to vary less with time as the repetition frequency increases.

Next, we shall consider the loss of electron energy due to collision with gas molecules.

The amount of energy loss due to collision depends on the kind of collision, elastic or

(~.l

inelastic. Cravath showed that the average energy lost by an electron in an clastic collision with a spherical molecule of mass IvI is a fraction of its energy given by

8 mM Q .Q

f = --3---.(ni -1 !Vi)

^-:l-

(1 - - u .) = 7) ( 1 .- --'G') ·(a)

where

8 mM

7J

=---~

-

3 (m+MF ···(1(1)

and u and Q is the average energy of electrons and gas molecules respectively.

Thus the rate of electron energy due to collision is

WI =~_"l (u-,Q) ···nI)

•••••••••••••.•••••••••••.•••••.••.••.••••••••••••• (J2l

Then the equation for the energy of electrons is given by -di,=WR du -WI

In general, it takes time for the energy of electrons to attain the stable state of Maxwellian distribution from that other than Maxwellian, the time of relaxation, however, shall be assumed not more than the mean free time of electron.

For Maxwellian distribution of electron energy, r is expressed by

- B A

r = 7-=f-- •.••.•.•.•.•.••..••.•.••.•••.•••..••••••.•••••••..• (13)

•.•••••.•••••••••••••••••.••••••••..•.• '" •••••.••• (14)

••••••••••••••••.••.••••••••••••••••••••••••••••••• (1;1)

where T is the mean free path of electron, T the electron temperature and B =/~~~- -

k is the Boltzmann's constant.

Putting 0:3) into (6) and (I]) and remembering that u=3kT/2, we have

dT - e:!(t) » ~-'----(T T )

-at= C J. V' c.-cT'c,-- - -IiI V T -

H

T s is the gas temperature.

(l5) is the basic equation of the electron temperature for the case where the variation of the field is small in the mean free time.

The mean free path generally depends on the electron energy, but as other authors did, we assume that it is independent on the energy. This assumption holds good for helium.

S:ep R~sponse of ~he Eladron Ternper aeure

We shall at first consider the response of the electron temperature when a d.c. field of the intensity Eo is suddenly impressed to electrons in a gas.

The basic equation in this case is

... ··•··••··· .. ·.... •·.. •.... ·Olil

Solving on the initial condition that T=T

o

at t= 0,

•••••••.•.••••••••..•••••••••••.•.•••.•.••••••••••. (17)

where

D, = I( T{_)'~-BC-G~O)~ +_~._

D~ ⁼ I (l'R~-_-F ^{+ Be} (J.~QJ~~ ^{_T R_}

2 71 2

.. ·· .. •••••• .. •.. ·• .. ••• .. •.. · .. •.. •··•• .... •••• .. ·(181

••••....••...•.•....••..•.••.••.•...•....•..••. ·(t9)

The final steady temperature, T"" can be obtained by putting t =

⁰⁰

in (17)

T",=D

1

t,.;,lQ)

Epuilibrium between the rate of energy gain and that of energy loss is to be established at the steaby state, and this condition is

•••••••.•••••••••••••.••••••••••••••••••••••••••••• (:21)

The solution of the above equation is obviously identical to t.,)(l).

It is usual that the condition

.•.•.•••••••••••••••.••••.••••••••.•••.•.•••.•••••. (2'1)

is valid, (lij can be simplified to

... (23)

and 00 can de written

- - T

T _... = I

_~r;~

^{BC l Eo + _!L.} ₂ ... (2.J)

o .. ,~ .. • • •

.1: .JT:

t - - -

Fig.!

The mean free path is about

. .

:

^I

131

~.--"

., (I."".

T~,

...

,,!

1 , ,

1-.,01 ,~~.

r.

I t 1t

Y

^I

I

I..," [~ T_

I _{II V I} II

y-- ^-I _~bf; ^\1 _I

^{/ v}

^{I I}

LL _{I ...} Uk _j/~ ^{1-- L.-:;}

^~v

^{I I I}

' ~'- •• ~ f:::/ II

... ^-

-...-

~

...

.. ^," -.

-' r

I

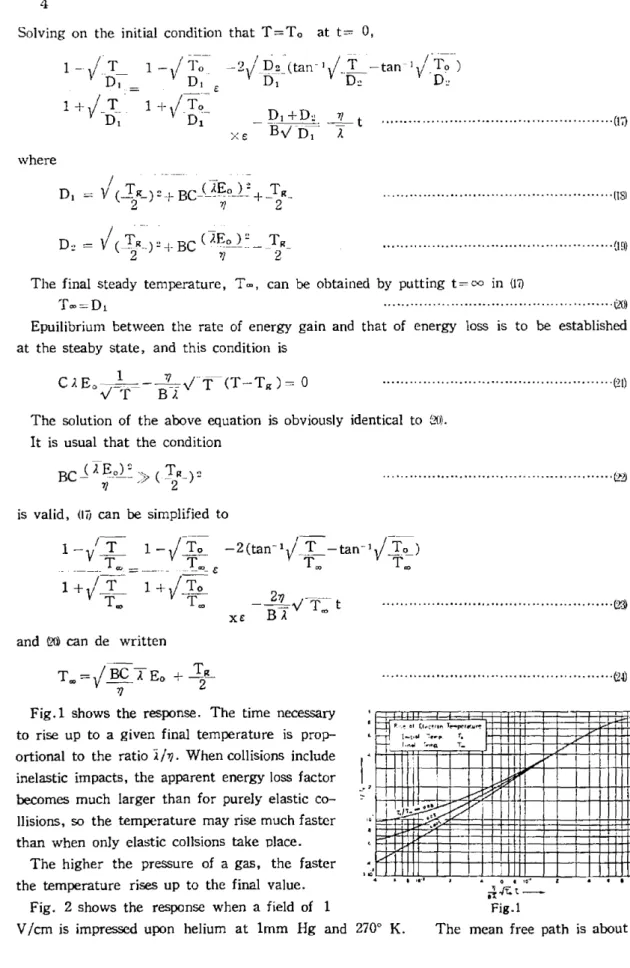
Fig.l shows the response. The time necessary to rise up to a given final temperature is prop- ortional to the ratio ~/7). When collisions include inelastic impacts, the apparent energy loss factor becomes much larger than for purely elastic co- llisions, so the temperature may rise much faster than when only elastic collsions take place.

The higher the pressure of a gas, the faster the temperature rises up to the final value.

Fig. 2 shows the response when a field of 1

V fern is impressed upon helium at Irnm Hg and 270

⁰

K.

5

••

~

^{" , of}IItull~J T,~,

""'~'-",~'

:n~·K

--- ^~-

fi"->! '"",

'''.:.ov'"

~t-I~~ I"l1l!l4t :-1~·K

,

V

v

/ 1 If.

v

v

...1-'

V

^{, /}

.

r' >

. .

^{eIll' ~}

..

f :

5.3/10-~cm and the energy loss factor for elastic collision is about 3.63:<10-

⁴

in this case. The final steady temperature is about 14,OOocK.

Next, we shall consider the fall of the temp- erature after the field is removed. Since electrons cease gaining the energy from the field imrned- iately after the removal of the field, the equation for this case is

Fig. 2

... (:2.:\)

Solving the equation on the condition that T=T'o at t=O, we have

...•.•...•... ···(2(;)

llg~~_~~ 15:-- ^{1 _ < - B'Q;: ,F'r;- t}

1_ ^{T_ +1} /J~ ⁺¹

'r, T

g

Fig. 3 shows the result. The time necessary to to fall down to the gas temperature from a given initial temperature is also proportional to the ratio T / ^7j.

Fig. 4 shows the decay of the temperature in helium at I mm Hg and 270

⁰

K from the initial temperature of 14,000

⁰

K.

Fig. 4

r",u",I[IrrtronT(',.,:>.:rJt"r~

{ !", t,

J!

'-,·.,P

^1·\:'OO·K

. r,M'

^T\,mp .n~'",

~('~"'lttl l"-l!nl/~ .:'73·K

\

\

\

_f---

t - -

\

I

\

1\

- ~

^~~

^{- - -} -

^-

I---~~-

~ ^-

^~-

^{--- - c---}

1 -

---

f---

~ ^{r--- --}

^I~

f - - -

f--~ -

'-, ^{- -}

--- _~ -.:.:.:.::

^~

--

-

.r.

'0

I:

Fig. 3

I~ 1s z o :,4 ~.Il

u~ ^{.[T; t}

_L -

r"'l of

Elect.ron

TcmpuJturc

^{l -}

f - -

Jnilodl Temp. T:

^{f -}

\\ _{FiMI T('mp. T9}

f - -

.~ ~

-~

to-.'{.-{;.

-~ _~\ ^\\

""

~ -,

:::::"... r:::::=;:::

_ \

~~ ^{3 ~ - - - - -}

^{- ~ .~I ~}

^{---= - -}

~

&1\ ^~

^{f---. ! -}

, ~

~

^{- - , ~}

~ _~ -

^~

^----=

~

^,~

1\ -. -- ^-- "'"-- -

1\ ~

1'\ ^... ---

, r-- I"-- -

ID o 0.40 1[1

-,

By comparing Fig. 4 with Fig. 2. we find that the fall of the temperature is much slower than the rise.

When a field whose waveform is rectangular as shown in Fig. 5(A). the response of the

temperature to the field might be such as shown in Fig. 5 (8) . At a lower frequency of

repetition, the temperature rises up with wider steps in the mark interval of the field and the final state can be attained with a smaller number of repetition. whereas the decay of the temper- ture in the space interval of the field is more remarkable than at higher frequency.

To compute the response of the temperature to a rectangular field. (Ii) and (26) have to be utilized alternately for the successive mark and space interval of the field till the steady condition is attained.

(8)

Respons\." of Electron T~rnpl'r<liun" to

il

Redo.'lnguJ,)r

_W~V~

Field.

t - -

T",-- - - -

t - Fig. 5 Eledron Temperature in a Sinusoidal Field

Putting e(t) ="';2 E sinet in U~, we have

••••••••••••••••••••••••••••••••••••••••••••••.•••• (27)

no 5P<-~"'~ll«I""T_f'O">l>o"'U~,tr-

V ^{e---- r-,} 1~1"""':"'.>I r~ld.

OJIT7V!O'Itlll'l"l ....

...

IhI~"1I!rI ."'11II"I"177~""

\ r

I t-

'",

- t -

I---- f--

-

1--1\

^.~

^-

\ ^-

1 - -

·~t ^{- e-- -}

^{~-l -r----}

,.'" ^{e-- -\}

^{-f -- ~}

^-

^{1 -}

v ^-

^{I - - - - 1 ---~ --~>---}

.' ^{- -}

- ; 7 ..-::

• f---.

r;..

^1--

_

^.

_--

t - - - I - - _.

_.

1---~

. -

_/

. ^-- _1/ V

~ c

which is nonlinear and can not be solved analytically.

To find the general characteristics of the response of the electron temperature to a sinus- oidal field, we shall take an example where a sinusoidal field of O.707V fcrn effective is impressed upon helium at 1 mm Hg and 273° K.

Fig.6 shows the results of numerical computation. At a frequency as low as lOke, the temperature rises up to about 14~ ()(X)0 K in the first quarter cycle, which corrresponds to the steady temperature for the d. c. field of 1 V/ em,

the peak value of the a.c. field. The temperature then falls down to about 3,000

⁰

K at the end of the second quarter cycle, and it again rises up to 14.000 OK by the end of the third cycle.

Thereafter a progress identical to the second quarter cycle repeats in the fourth quarter cycle.

Thus, the steady state can be attained in only one cycle of the field, and the pulsation of the temperature in the stead ystate is remarkable at this fpequency.

At a frequency as high as 10 me, the tempe- ....

^r:>o

~

Awl.~("';I_

rature rises up to not higher than about 770

⁰

K Fig. 6

by the end of the first quarter cycle and thereafter it continues to rise for a moment. There

is not any dip .of the temperature in the descending period of the field. It rises again up to

about 1,400° K by the end of the third quarter cycle and then continues to rise to a crest

value of about 1,700° K at the end of one cycle. As the steady mean temperature is about

10,0000 K·in this case, the steady state can be attained after several cycles of the field,

7 and the pulsation of the temperature around the mean may be small at such a frequency.

The mean free time corresponding to the mean free patcf 5.3 ^Y 10- ~cm for helium at 1 mm Hg and the electron ternperture of 10 ~ 000" K is about 8.5>: 10-

J (\

£ec., SO about 120 collisions occur in one cycle of 10 me. The product ^w-:, shift of the phase of the field in the mean free time, is about 5.4>: 10- ~ in this case.

If the frequency of the field is sufficiently low that the equilibrium is established at every instant between the time rate of energy gain and that of energy loss, the steady temperature can be found by

...es

Solving with T

t

T = I~-i~~)

^Z

^{+- Be -} (-;:-El~ ( ¹ _-~:-s2wt) ⁺ _{J'~_}

2 ~ 2

If the condition (z"21 is valid.

/2BC- i . '

T = V-- ---- ), E

^I

sinot

11

I

and the value averaged over one cycle of the field is

Next, we shall consider the steady condition.

Let

then,

e ² ( t) = ^E e

²

+ f(t)

... f2!))

...•...••...•...•...•.

"~l])

... ··· .. · .. ···· .. · .. · .. · .. ···r;l)

••.•••• , .•.••.•••...••..• , ..•••.••.•• , •••.•.••••••• (:)2)

..•.••..•..•...•..••.•..•...••...•..•...•.

'~33J

where E _c is the effective value of e(t) and f(t) is the time dependent component.

We separate the temperature into an a. c. and a d. c. component. Thus we put

T=T

m {

1 +~(t)}

Putting l:>~ into (IG) and neglecting T

R:

for simplicity

^t

... '" ,

'l:~~)

_~~1" ~~t-=BC-(~-;~)--= ~-,:f.:-{l f(t)}--v·'t~r} ··· .. ··· .. ···n~t

With regard to the mean temperature in the steady state, the following relation holds from C35l.

from which we have

-

Tm ⁼ 1-~~-.fEc

7J

. (:)J)

... , ..•... ···tJi')

8

Thus. if a large number of collisions occurs even in the shortest period of the component wave in the periodically varying field. the mean temperature can be determined by the effective intensity of the field and is independent of the frequency of the component wave.

Putting ^(:3.\) into t.,=)),

AF(t) =-_l7- VT- - - ^{1 __ -: (f(t) --F(t){ 2 +F(t)}] (33)}

dt Bj '" « ^{1 + F(t)}

The periodic solution of (3-~ gives the waveform of the ripple in the steady temperature.

00, however, can not be solved analytically.

The amount of ripple may be small compared to the mean at higher frequency of the field, so we shall now discuss where F ^(t) <1. ⁽³⁸⁾ can be simplified to

eIF(t) 1J { (

- - = - - - f(t) -2F t)}

dt

^t"m

...

~)

which is solvable. ~m is the mean free time corresponding to the mean temperature.

For a sinusoidal field,

where

tan e = _17_

W1:'m

'" ..•••.•.•.•••..•..••••...••.•.••.•••.•••.•••••. '(40)

... ·(to

By the assumption, (40) is valid only for (w)rm)2}> 1J~. then F(t) = __ 1 __ sin2wt

2wt'"m

•••..••..••••••••••.••.•••..•••.•••.••...••••••••• '(421

Thus, for a given gas the amplitude of ripple is proportional to the square root of the mean temperature and inversely proportional to the frequency of the field.

The lowest frequency that satisfies the condition (wrm)

2

> 100172 is about 670 kc for our example and the amplitude of the ripple amounts to about 5 % of the mean

t

so the ripple may be negligible above this frequency.

When the frequency of the field is so high that intensity of the field varies appreciably in the mean free time of electron, (;.'7) tends not to hold. tnp in (3) is diverse for each free path and electron. so the energy gain should be averaged over the time or the phase angle.

For

E

(t) = V 2· E sinot , average energy gained by an electron in a free time is

~1! 0 -

t

CeE )

2

1 S S - ~-{ S . ^{d }" d J d ( )}

Wg =-_.---._- ---- ( e r smot t · r wt

fit' 2it'

^{0 _a>}

t-1:"

(eEwr)

²

(eB TE)

²

= m(lJZ{ 1~- ^(wr) 2} = mrCBWA) 2 -+ -t} ...

^(~

Equilibrium should be established between the rate of the gain of energy and that of loss of it, so

.. · .. •.... •• .. · .... •••·• .. ···• .. · .. •... · .. •.. ·(44)

9 The solution is

For a given effective intensity of the field, the electron temperature decreases as the frequency increases, and if (Cu.):! > I, the temperature is given by

2e~ E

T=T g + --(---)~

3mk7}

^W

••••••••••••••••••••.••••••••••••••.•••••••••••••••(46)

., ....••...•... ·(4i)

For helium at 1 mm Hg and 273

⁰

K, the lowest frequency that satisfies the condition

(wr)~>100 is about 1,870 me at the temperature of 10,000

⁰

K, and, in order to get this temperature at this frequency of the field, the field of about 5. 9Vfern effective must be applied. The temperature which can be attained by the field of 0.707 Vfcrn effective is only about 370

^{0 K}

at this frequency.

Densi~y of Electrons in the Luminous Cloumn of H.F. Gbw Discharge

At low current density in the luminous column of glow discharge, the energy distribution of electrons will not be Maxwellian, but at higher current density and with a small potential gradient as usually observed, the distribution again approaches to Maxwellian. With their much higher temperature than the positive ions, electrons diffuse more rapidly than positive ions, thus they tend to accumulate on the wall surface of the discharge tube, charging it up to a negative potential. As a result, positive ions are drawn to the wall and there quickly be neutralized. This type of diffusion is termed ambipolar diffusion. The ambipolar coefficient of diffusion is given by

D, = ----.Lb+ T e

where b , is the mobility of positive ions.

Let us call z the number of times per second that an electron in its random motion gets the ionization energy and is able to ionize the gas atoms, and' N the numbr of electrons per unit volume, the time rate of the change of the change of electron density is given by

If we assume cVi}'-2kT, ^Z is given by -'kT' eVi

z =QV·'1.~

^E

where

•..•...••....••..•...•..•...•...•..

(~&

.•••.•••.••..•.•.••.••..••.••••.•••••.••.••.••.. ,. '(48}

···00

Q =~~:~(2~e~ ^{__. / k}

J. V nm ³

Vi is the ionization potential and a the constant which depends UIXlI1 the kind of gas.

If we put T~--= T

^{m {}

1 -j F(t)}, and assume that F(t).-> 1 , zo __ = Urn {I --\- SF(t)}

D a

..•... ··(50

10

where

and

Urn = ---~Q-'=--€-p

kb

+

VT m

{3=~_I-

eV' kT m

" '"

'~2l

•.••....•...•.•••••....••..•.•••.••••..••••.••..•••

(5.~

We now consider a cylindrical discharge vessel. Taking the axial symmetry of the features of the luminous column into account, we have

... 54)

··· ..···..·· ..···..·..··· ..·..···ffl Next, we separate the electron density into a d.c. and an a. c. component,

N=N

m {

1 +G(t)}

in which G (t)« 1. Putting 50 and IP5) into (iH),

{ 1 + G (t) }( j:N ^m + _1~ ^dN m ₊ Urn N rn ) + Urn _~Nrn F(t) = N rn dGJ!2 _~

~2 r ~ ili

Fquilibrium should be established between the mean I ate of electron creation due to ionizing collision and that of loss of electrons due to ambipolar diffusion at steady state, so we have

d2N~_+_1_ dNrn + _{Urn Nm=0,}

dr ² r ~ ... (5t)

from which the radial distribution of the mean electron density can be determined as usual.

So,

dG (t) = U rn$F (t) dt

Putting M into ~, we have

...(58)

... C5!J)

G (t) = . .!Jrn_~V~II11.~ ^cos2wt

4w~ i B .

The ripple of the electron density is inversely proportional to the square of the frequency of the field.

Conclusion

As the results of the study on the response of the electron temperature to a varying field, the following conclusions have been obtained.

When a large number of collisions occurs between electrons and molecules in the mean free time of electrons,

(1) As regards the step response, the time necessary to reach the steady temperature is inversely proportional to gas pressure and the energy loss factor.

The temperture rises up more rapidly after a d ,c. field is suddenly impressed than it

falls down after the field is removed.

11

(2) As the frequency of a sinusoidal field is increases, the temperature rises with smaller steps and it takes more cycles than at lower frequencies to reach the final steady tempe- rature,

If the amplitude of the ripple of is much small compared with the mean. it is proport- ional to the square root of the mean temperature and inversely proportional to the frequency of the field.

The ripple of the electron density in the luminous column of h. f. glow discharge is inversely proportional to the square of the frequency of the field.

As the variation of the field becomes remarkable in the mean free time of electrons, the temperature tends to decrease as the frequency increases, and it is inversely proporti- onal to the square of the frequency at sufficiently high frequency.

The author wishes to thank Mr. M. Matsumoto for the assistance in this study.

References

(l) J. S. Townsend, Phil. Mag., 13, 752. 1932.

(2) K. Yamamoto and K. Nobata, J. I. E. E. of Japan, 69, 47. 1947.

(3) M. Konorni, Bull. Kyushu Inst . of Tech., 3, 3, 1953.

(4) M. Konomi Trans 1. E. E. of Japan, 4, 365, 1952.

(5) A. M. Cravath, Phys, Rev., 36, 248, 1930.