n $%&'() r r ()= ()= z z r r ! A 1 ! cos2 w pl n ! 1 n ! 2 nR S

(1)

OS1125

＜M&M2014カンファレンス・2014年7月19〜21日＞

1. 緒言

近年，加工技術の進歩により微小な構造体が製造され，

ナノスケールでの摩擦特性を調べることが重要となり，

ナノトライボロジーと呼ばれている．微小な探針と試料表面に働く力を測定する原子間力顕微鏡(AFM)により表面の凝着力や摩擦力の測定が行われている．探針はスキャニング回数を増やすごとに摩耗によって先端の形状が変わっていく．Griersonら⁽¹⁾は摩耗した探針の形状を指数則に近似して平面との凝着解を導いた．また実際の材料は平面ではなく微小な凹凸を有する面である．Guduruは

(2)解析的に凝着問題の解を得るために軸対称の波形状を有する面に対して球状圧子が接触する問題を解いた．

本研究では指数則に従う形状の圧子と軸対称の波形状を有する等方性弾性体の接触・凝着問題を解く．

Lennard-Jonesポテンシャルに基づく凝着解析の結果と比

較し，解析解の妥当性を検討する．

2. 指数則形状の圧子と波状表面の接触問題

ここでは，軸対称の形状を考え接触問題を解く．図１に示すように，剛体圧子が軸対称の波に近づく問題を解く．指数則に従う圧子の形状を以下のように定義する

z_pl

( )

r ⁼ ^r

n

nR^n!1S^n!2 ⁽¹⁾

ここで，Rは圧子半径，Sは圧子の鋭さを表す，nは指数，

rは原点からの距離とする．n=2のときに圧子形状は球状

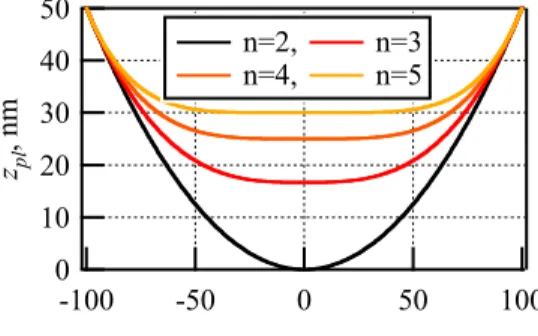
になる．図2にR=100, S=1の圧子形状を示す．ここでは，

r=100で圧子の位置が一致するようにした．指数nの値が大きくなるに従い圧子の先端が平らになる．次に，軸対称の波を有する面は以下の式で表す．

z_w

( )

r ⁼^!A^$_%^&^1!^cos^2"r_# ^'₍⁾ ⁽²⁾

ここで，Aは振幅，λ^{は波長である．式}^{(1)および式}^(2)よ

指数則形状の剛体圧子と弾性波状面の接触問題

林高雄^*1，古口日出男^*2

Contact problems of a rigid indenter for power-law profile and

an elastic wavy surface Takao HAYASHI

^*3

and Hideo KOGUCHI

*³ Nagaoka University of Technology, Dept. of Mechanical Engineering Kamitomiokamachi 1603-1, Nagaoka City, Niigata, 940-2188 Japan

In this study, the contact and adhesion problems of power-law profile indenter and wavy surface is considered. The solution of contact problem based on the axisymmetric contact is solved. The adhesion problem is solved based on the JKR theory. The solution is compared with the adhesion analysis based on the JKR theory.

Key Words : Contact mechanics, Adhesive contact, Wavy surface,

Fig. 1. Model for contact and adhesion problems

50 40 30 20 10 0 zpl, nm

-100 -50 0 50 100

x-coordinate, nm n=2, n=3 n=4, n=5

Fig. 2 Profiles of Indenter

*1正員，長岡技術科学大学（〒940-2188 新潟県長岡市上富岡町1603-1）

*2正員，長岡技術科学大学

E-mail: hayashi_takao@stn.nagaokaut.ac.jp

(2)

2

り二面間の初期間隔は以下のようになる．

g r

( )

⁼ ^r

n

nR^n!1S^n!2 +A 1!cos2"r

#

$

%& '

() ⁽³⁾

接触半径がaのとき，軸対称問題の押し込み深さδ^は式 (3)を用いて以下のように書くことが出来る．

!_con

( )

a ⁼^a ^g^"

( )

^#

a²$#²

0 d#

%

a

= &a'

(

n/ 2

)

2R^n$1S^n$2' n+1 2 (

)* +

,- +&²aA

. H₀ 2&a . (

)* +

,- (4)

ここで，Γ(･) はガンマ関数，Hn(･) はn次のStruve関数をそれぞれ表している．この式でn=2としたときに球状圧子のGuduruの解と一致する．軸対称の圧力分布は以下の式より求めることができる

p_con

( )

r ⁼^E

*

!

"

# $

( )

$²%r² d$

r

&

a ⁽⁵⁾

ここで，E^*=E/(1-ν²⁾は複合ヤング率である．式(5)に式(4) を代入すると

p_con

( )

r ⁼^E

*

! l_n+4!²A

"² a²#r²

$

%&

+!²A

"

H₀

(

2!'/"

)

'²#r²

r

(

a ^d'

#2!³A

"²

'H₁

(

2!'/"

)

'²#r² d'

r

(

a ⁾

*+ (6)

lnの部分ををn=3~5について計算すると以下の式になる．

l_n=3= 3!

8R²S

{

a a²"r²

(

2a²+3r²

)

+3r⁴log a+ a²+r² r

#

$

%%

&

' (( )

*+ ,+

l_n=4=8

(

a²+2r²

)

9R³S² a²"r² l_n=5= 15!

128R⁴S³

{

a a²"r²

(

2a²+3r²

)

+3r⁴log a+ a²+r² r

#

$

%%

&

' (( )

*+ ,+

(7)

式(6)を接触領域で積分することで接触荷重Pを求めるこ

とができる．

P_con

( )

a ⁼²^!

"

₀^a^{rp r}

( )

^dr

=2E^* L_n+4!²a³A

#² +!aA

2 H₁ 2!a

#

$

%& ' ()

*+ , -!²a²A

2 H₂ 2!a

#

$

%& ' ().

/0

(8)

ここで，Lnはn=3~5について

L_n=3= 3!a⁴ 16R²S L_n=4 = 8a⁵

15R³S² L_n=5= 5a⁶!

32R⁴S³

(9)

となる．

3. JKR理論による凝着問題

ここでは，導出した弾性問題の解を凝着問題に拡張する．JKR理論において凝着力と押し込み深さは以下のように書くことができる．

P_ad=P_con

( )

a ^! ⁸^"#^a³^E^*

$_ad=$_con

( )

a ^! ²^"#_E*^a

(10)

ここで，γは二面間の表面エネルギ，P_con(a)およびδcon(a) は凝着を考慮しないときの接触荷重と押し込み深さである．式(8)と式(6)を式(10)に代入すると

P_ad

( )

a ⁼^2E^* ^Ln+4!²a³A

"² +!aA

2 H₁ 2!a

"

#

$% &

'( )*

+ ,!²a²A

2 H₂ 2!a

"

#

$% &

'(-

./, 8!0a³E^*

(11)

!_ad

( )

a ⁼ ^"^a#

(

ⁿ^{/ 2}

)

2R^n$1S^n$2# n+1 2

%

&

' (

)* +"²aA

+ H₀ 2"a +

%

&

' (

)* $ 2",a E^*

(12)

となる．これらの理論解を用いて，凝着問題を調べる．

4. 解析結果

はじめに，本研究の解をLennard-Jones型ポテンシャルをもとにした凝着解析の結果と比較する．凝着解析ではモデルを格子点に分割して解析を行う．各格子点での二面間の表面力PLJを以下の式を用いて求める．

p_LJ

( )

x,y ⁼^8!₃_" _{g x,}

( )

^" _y

#

$

%%

&

' ((

3

) "

g x,

( )

y

#

$

%%

&

' ((

* 9

+ ,, ,

-

. // /

0 1x1y (13)

ここで，ε^{は平衡原子間距離，}^g^{は二面間の格子の間} 隔，Δx, Δyはそれぞれx軸方向とy軸方向の格子点間隔を示す．二平面全体に作用する表面力を式(13)から求めた各接点での表面力の総和とする．表面形状は理論解と同様に式(1)と式(2)を用いて各接点での

(3)

3

高さを決定した．凝着解析では圧子の位置を入力とし，反復計算によって二平面間に作用する表面力と変位を決定する．

解析条件として，材料は銅を想定し E=128GPa,

ν=0.34，二面間の表面エネルギはγ^=2.5N/m ^とした．

圧子の形状はR=100nm，S=1，n=3 である．解析で得られた凝着力を JKR 理論による最大凝着で正規化する．JKR理論での最大凝着力は

P_JKR=3

2!"R (14)

である．図3に理論解とL-Jポテンシャルに基づく凝着解析の結果を比較する．凝着解析において二面間の平衡原子間距離はε^=0.2nm^とし，^Adhesion^が圧子を表面に近づけ，Detachmentが表面から離す過程を示している．理論解と凝着解析の結果がよくあっているため，理論解は正しいと考える．また，凝着解析で，圧子を離す過程において引き剥がれが発生するのは理論解で最大凝着力が生じた点に近いので，

理論解で引き剥がれが発生する点を最大凝着力が生じた点とする．

つぎに，理論解を用いて波の高さの影響を調べるため，振幅 A の値を変えて各条件での最大凝着力 P_maxを求めた．図4にそれぞれの解析結果を示す．

圧子の指数nが大きくなるほど最大凝着力が大きくなる．これは図１のように指数が大きくなると圧子先端が平らになり，凝着半径が大きくなるため最大凝着力が大きくなったと考えられる．また，振幅A を大きくすると最大凝着力も大きくなる．

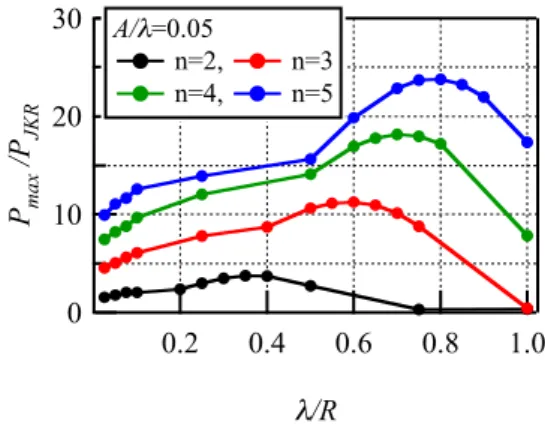
波長λを変えたときの最大凝着力を図5に示す．

ここでは圧子半径Rを用いて無次元化している．最大凝着力は図4の振幅を大きくしたときと同じく，n を大きくすると大きくなる．さらに，各指数nでの最大凝着力は極大値があり，指数nを大きくすると

極大点のλは大きくなる．

5. 結語

本研究では，指数則に従う圧子と波形状の表面の接触・凝着問題の解を導いた．解析解とL-J型ポテンシャルに従う，凝着解析と比較し両者がよくあっていたことから，理論解の正しさが確かめられた．

また，凝着解析との比較で，引き剥がれは理論解の最大凝着力の点で発生することがわかった．波の波長を変えて最大凝着力を求めたところ，最大凝着力に極大点があり，指数が大きくなるほど極大点の波長は大きくなる．

文献

(1) Grierson, D., et al., Adhesion of nanoscale asperities with power-law profiles, Journal of Mechanics and Physics of solids, Vol. 61, (2013), pp. 597-610.

(2) Guduru, P.R., Detachment of a rigid solid from an elastic wavy surface: Theory, Journal of Mechanics and Physics of solids, Vol. 55, (2007), pp. 445-472.

Fig. 3. The relationship between normalized applied force and distance between surface and indenter

60 40 20 0 Pmax/PJKR

0.5 0.4 0.3 0.2 0.1 0.0

A/!

! /R=0.05 n=2 n=3 n=4 n=5

Fig. 4. The maximum adhesion force for each value of amplitude

30 20 10 0 Pmax /PJKR

1.0 0.8 0.6 0.4 0.2

!/R A/!=0.05

n=2, n=3 n=4, n=5

Fig. 5. The variation of maximum adhesion force for each value of wavelength