第
1
章 物理入門
1.1
相空間
古典力学,つまりニュートン力学 (Isaac Newton, 1642–1727) は 1. 等速直線運動: 力が加わらないときには等速で直線的に運動をする 2. 運動方程式 (力は加速度に比例する) F = ma 3. 作用反作用の法則; 机の上のボールは机がボールの重力に等しい力を与 えるから机にめり込まない. で記述されます.ここで F は力,a は加速度を表します.2 番目の運動方程式 を考えましょう.時刻 t における位置を x(t) で表せば,その微分 v(t) = x′(t) が速度,さらに微分をすれば v′(t) = x′′(t)が加速度を表すことはわかるで しょう.力 F は質点の位置と速度で決まるとすれば,運動方程式は,加速度 が位置と速度から決定されることを意味しています. 私たちは質点の運動を考えるとき,その位置のみに注目してしまう.だか ら,私たちの世界は 3 次元だなんて簡単に言ってしまうのでしょうが,質点 には速度があり,速度も表すには 3 次元の空間が必要です.運動方程式をみ れば加速度は位置と速度で決まることになるはずですから,質点の運動は位 置を表す 3 次元,速度を表す 3 次元のそれぞれの点が定まれば,運動は完全 に記述できることになります.いっそ,位置の 3 次元と速度 3 次元,あわせ て 6 次元の空間の 1 点とみなしてしまえば,質点の運動は完璧に記述できる ことになるでしょう.この空間を相空間といいます.質点が 2 つならば,そ れぞれに位置と速度が 6 次元ですから,合わせて 12 次元の空間が相空間で あることになります.質点が増えればどんどん大きな次元が必要になるので すね. 例 1 もっとも単純な例ですが,質点の落下を考えてみましょう.落ちるだけ なのですから,位置も 3 次元で考える必要はないでしょう.高さの方向の 1 次元だけにしましょう.同様に速度方向も縦方向のみを考えれば,質点の運 動は 2 次元で記述できることになります.質点の質量を m とすれば,下向きv x 図 1.1: 相空間における質点の運動 に重力 mg が働いているから運動方程式は x′(t) = v(t) mv′(t) = −mg と表されることになります.これは容易に解けて,時刻 0 での位置と速度を x(0) = x0,v(0) = v0とすると x(t) = x0+ v0t− 1 2gt 2 v(t) = v0− gt となります.したがって,t を消去すると質点の落下の運動は x = x0+ v02 2g− v2 2g と質点の軌道は図 1.1 のように (x, v) 平面の放物線として表されることがわ かりました. 例 2 もう 1 つ,単純なモデルであるふりこの運動について述べておきましょ う.1 つの平面を移動するふりこは鉛直線からの角度 θ とその角速度を考え れば記述でき m す.ふりこのおもりを m,長さを l とすると (図 1.2) lθ′ = v mv′ = −mg sin θ となります.このままでは解けませんが,θ が十分に小さいときには sin θ∼ θ とみなせるので,上の方程式は lθ′ = v mv′ = −mgθ
θ θ mg mg sin θ 図 1.2: ふりこの運動 で近似できるはずです.この方程式の解は ξ = lθ + i √ g lv とおけば ξ′=−i √ g lξ となるので θ(t) = A sin (√ g lt + ω0 ) で与えられます.ここで A や ω0は最初の位置や速度で決定されます.予想 通り,ふりこは図 1.3 のように周期運動がすることが導かれました.2 次元 図 1.3: sin θ = θ とみたときの,ふりこの相空間での運動 の相空間の各点 (x, v) からその速度にあたるベクトル (x′, v′)を生やしてみま
しょう.相空間の運動はこの速度ベクトルが接線になるように移動するわけ ですから,この図をみるだけで大まかな運動がわかることになります.振り 子では図 1.3 のようになり,回転運動が見えています.これをベクトル場と いいます. 図 1.4: 本当のふりこの相空間での運動 もっとも, ふりこの振り幅 θ が大きくなると sin θ∼ θ とみなすことがで きなくなりますので,その解を簡単には表すことはできません.本当の解は 微分方程式を解くことができないので記述はできませんが,図 1.4 のように ベクトル場に表すとなんとなく解が見えてくることがわかるでしょう.θ が 大きいところでは図 1.3 と大きく異なる挙動をします. 以上の例からもわかるように,位置だけではなく速度も含めて考えると見通 しがよくなることがわかりました.
1.2
微分方程式とベクトル場
2次元の微分方程式を考えましょう. dx dt = f (x, y) dy dt = g(x, y) 微分方程式を解くとは,この式をみたす (x(t), y(t)) を求めること,すなわち x′(t) = f (x(t), y(t)) y′(t) = g(x(t), y(t)) を求めることです.しかし,通常の方程式は解けることはほとんどありませ ん.そこで,せめて与えられた点 (x0, y0)の近所の行動だけでもわかる努力 をしてみましょう.それにはテイラー展開を用います.まず,(x0, y0)の近くでは dx dt = f (x0, y0) dy dt = g(x0, y0) と考えられるはずです.これは容易に解けて,t = 0 で (x0, y0)にいるとす ると x(t)− x0) = f (x0, y0)t y(t)− y0 = g(x0, y0)t と直線的に動くことがわかります.問題は f (x0, y0) = g(x0, y0) = 0となっ てしまった場合です.この場合には今の近似は成り立たなくなります.この 場合を特異点といいます.こうなったら,テイラー展開を一歩すすめて dx
dt = f (x0, y0) + ax(t) + by(t) = ax(t) + by(t) dy dt = g(x0, y0) + cx(t) + dy(t) = cx(t) + dy(t) まで考えればいいでしょう.ここで a =∂f ∂x(x0, y0), b = ∂f ∂y(x0, y0), c = ∂g ∂x(x0, y0), d = ∂g ∂y(x0, y0) です.これはベクトル x = ( x y ) と行列 A = ( a b c d ) を用いると d dtx = Ax と線形の微分方程式になります. まず,もっともやさしい例から始めましょう.それは行列 A が対角行列 ( λ 0 0 µ ) の場合です.この場合は,もとの形に戻せば dx dt = λx dy dt = µy
となって,2 つの独立な方程式が得られることになる.この時刻 t = 0 におけ る初期値が (x0, y0)である解は x(t) = x0eλt y(t) = y0eµt と解くことができます.次に簡単なのは A = ( λ −µ µ λ ) の場合です.この場 合には極座標 r =√x2+ y2と tan θ = y xに変換します.微分方程式は dx dt = λx− µy dy dt = µx + λy ですので, dr dt = d dt(x 2+ y2)1/2) = 1 2(x 2+ y2)−1/2 ( 2xdx dt + 2y dy dt ) = 1
r(x(λx− µy) + y(µx + λy))
= 1 rλ(x 2+ y2) = λr となります.一方, d tan θ dt = d dt y x= xdy/dt− ydx/dt x2
=x(µx + λy)− y(λx − µy)
x2 = µ x2+ y2 x2 および d tan θ dt = 1 cos2θ dθ dt = (1 + tan 2θ)dθ dt = x 2+ y2 x2 dθ dt ですので, dθ dt = x2+ y2 x2 d tan θ dt = x2 x2+ y2 × µ x2+ y2 x2 = µ となります.以上から dr dt = ar, dθ dt = µ を得ます.これは容易に解けて,0 での初期値 r = r0と θ = θ0のときの解は r(t) = r0eλt θ(t) = θ0+ µt
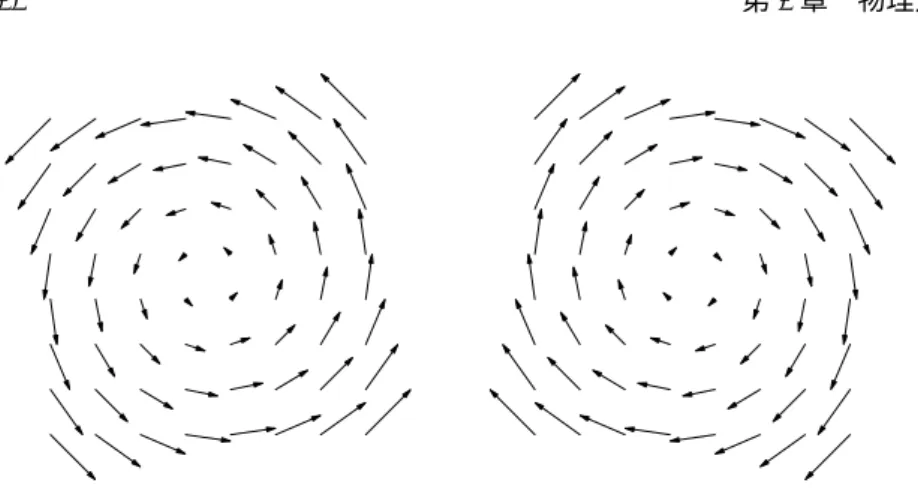
となります.すなわち,角度は一定の角速度 µ で回り,r は指数的に変化す ることがわかります.λ < 0 のときには原点に回転しながら収束し,λ > 0 な ら回転しながら無限に発散することがわかります.このとき原点を渦状点と よび.λ < 0 のときには安定,λ > 0 のときには不安定といいます.λ = 0 の ときには常に一定の円の上を回転するので,原点を渦心点といいます. いま 1 つやっておきたいのが ( λ 1 0 λ ) の場合である.この行列は,ジョル ダン標準形とよばれます.この場合はもとの形に戻せば dx dt = λx + y dy dt = λy となります.下の式はすぐに解けて y(t) = y0eλt,これを上の式に代入すると dx dt = λx + y0e λt となり,これは線形微分方程式なので,定数変化法で解を x(t) = C(t)eλt とおくと, dx dt = C(t)λe λt+ C′(t)eλt = λx(t) + C′(t)eλt により,C′(t) = y0を得ます.初期値を考慮すれば C(t) = x0+ y0tなので, x(t) = (x0+ y0(t− t0))eλt y(t) = y0eλt であることがわかります.ベクトル場を用いて解の概略を考えましょう. 1. λ, µ > 0のとき 2. λ, µ < 0のとき 3. λ > 0, µ < 0,または λ < 0, µ > 0 のとき 4. ジョルダン標準形で λ > 0 のとき 5. ジョルダン標準形で λ < 0 のとき この他に λ, µ が 0 に等しい場合もありますが,面白くないので省略しましょ う.これらのベクトル場はそれぞれ,図 1.5 のようになります. (1),(2),(4), (5)のときは原点を結節点,そのうち時間の経過とともに原点に近づいてくる
図 1.5: ベクトル場の図,結節点 (λ > 0 と λ < 0) 図 1.6: ベクトル場の図,鞍点 (λ > 0 と λ < 0) (3)と (5) の場合は安定結節点,(1) と (4) を不安定結節点といいます.(2) で は鞍状点といいます. 渦状点や渦心点のベクトル場は,図 1.8 のように,λ > 0 のときには,解 は原点のまわりを回転しながら遠ざかり,λ < 0 のときには近づく.λ = 0 の ときには,図 1.9 のように,原点のまわりをぐるぐるまわります.渦状点で も渦心点でも µ > 0 のときには右まわり,µ < 0 のときには左まわりになり ます. 定理 1 行列の固有値は det(xE− A) = 0 の解である.この方程式を固有方程式という.とくに A が 2 次正方行列なら ば,その固有方程式は x2− (Tr A)x + det A = 0 となる.ここで,E は単位行列,det A は A の行列式,Tr A は A のトレー
図 1.7: ベクトル場の図,結節点 (Jordan 標準形,λ > 0 と λ < 0) 図 1.8: 固有値が複素数の場合のベクトル場 (λ > 0 と λ < 0) ス (対角成分の和) を表す. この定理をみればわかるように実行列であっても固有値は実数とは限りません. 定理 2 2 次正方行列に異なる固有値 λ, µ があるとしよう.a = ( a1 a2 ) と b = ( b1 b2 ) を対応する固有ベクトルとする.すなわち,a と b は 0 ベクトル ではなく Aa = λa Ab = µy をみたすとする.このとき,この 2 つのベクトルを並べた行列 P = ( a1 b1 a2 b2 ) は P−1AP = ( λ 0 0 µ ) となる.
図 1.9: 固有値が複素数の場合のベクトル場 (λ = 0,µ > 0 と µ < 0) これを行列の対角化といいます.微分方程式 dx dt = Ax の左から P−1をかけると dP−1x dt = P −1AP P−1x となりますので,P−1x = y = ( y1 y2 ) とおけば dy dt = ( λ 0 0 µ ) y すなわち,対角行列の場合に帰着できます.固有値が複素数になるときには, 固有多項式は実係数の 2 次方程式ですから,λ± µ の形をしています.この 場合には行列 U = ( 1/√2 i/√2 −i/√2 1/√2 ) とすると (P U )−1A(P U ) = U−1P−1AP U = ( λ −µ µ λ ) と表せます. この他に,固有値が λ しかない場合には P−1AP = ( λ 0 0 λ ) と対角化でき る場合と P−1AP = ( λ 1 0 λ ) となる場合があり,下の場合がジョルダン標準 形です. 一般的な例を考えてみましょう.
問い 1 ボルテラの微分方程式 dx dt = x− xy dy dt =−y + xy の相図を描いてみよ. 図 1.10: ボルテラの微分方程式とファン・デル・ポールの方程式 この方程式は 2 つの特異点 (0, 0) と (1, 1) をもち,(0, 0) は鞍状点,(1, 1) は渦 心点になります.ベクトル場は,図 1.10 のようになります.このモデルは x をバッタ,y をカマキリと思ったときの生物モデルです.バッタは自分の数に 比例して増大しますが,カマキリがいると食われてしまって減少します.一 方,カマキリは自分達だけでは友食いをして減少しますが,バッタがいれば 増えることができます.このモデルの解はバッタとカマキリが増加減少をく りかえすという自然現象に近いものとなっています. 問い 2 次の相図を求め,解の漸近的挙動を推定せよ. dx dt = x 2+ y2− y dy dt = x− 2xy Aが 0 行列のときには,この方法だけでは解の全体像を想像することはでき ないし,この方法がいつもうまくいくわけではないことには注意しておきま しょう. 例 3 ファン・デル・ポールの方程式 dx dt = y dy dt =−εy(1 − y) 2− x
は ε = 0 のときには,x2+ y2の値は解の時間発展とともに変わりません,し たがって,円の上を回転する解になりますが,ε > 0 になると,1 つの周期解 が存在し,周期解の近くの解はその周期解に近づいていくことが知られてい ます.この周期解を極限周期解とよびます.この極限周期解は上のような不 動点の近傍での線形化では求められません.
1.3
万有引力と電磁力
2つの質量 M と m の質点があるとき,m には M から万有引力 F =−GM m r2 e が働くことが知られています.ここで e は M から m 方向への単位ベクトルで す.したがって,2 点間には引き合う力が働くことになります.地球の表面に 1kgの物体をおいたとき,地球の中心に地球の質量 M が集中しているとみな せますから,r = 6400km を代入したときに働く力が重力加速度 g = 9.8m/s2 になるわけです.いろいろな場所に単位重さををおいて力の働く方向と強さ をベクトルで表すと,ベクトル場のような図が得られます.2 つ質点がある 図 1.11: 中心力場と 2 質点の作る重力場 ときには図 1.11 の右図のようになります.位置の空間は相空間では質点の運 動を表すわけではありませんが,どのような動きをするかの示唆は得ること ができます.これを重力場といい,Gで表すことにします. 電気でも Q, q クーロンの電荷をもつ点の間にはクーロン力 (Charles Coulomb, 1736–1806) F = kQq r2e が働きます.重力場とは異なるのは電荷には符号があることです.重力場と 同様に各所に 1 クーロンの電荷をおいたときにその力のベクトルを描いた物を電場といいます.マイナスの電荷をもつ点が 1 つだけあるときには,プラ スの単位電荷は引きつけられるので,図 1.11 になり,プラスの電荷をもつと きには反発するのでベクトルの方向が逆になります.2 つの電荷がプラスの 電荷をもつと反発するので図 1.12 左図になり,2 つの電荷がマイナスの電荷 図 1.12: 電力場,反発と吸引 をもつときには,図 1.11 右図になります.2 つの電荷がプラスとマイナスの 電荷をもつときには,図 1.12 右図になります. N極と S 極がばらばらに存在することが確かめられたらば,磁力でも同じ 式が成り立つはずです.クーロン力や磁力でも電場Eや磁場Bを考えることが できます.電場はそこに 1 クーロンの電荷を置いたときにその電荷にかかる力 を表します.磁場ではそこに単位磁力をおいたときにその点にかかる力と言 いたいところですが,単位磁力という概念がありませんので,これでは考えら れません.クーロン力と磁力の間には密接な関係があります.電流が流れれば 磁場が生じ,逆に磁力が動けば電流が生じるという相互に同じような働きを します.これを実験的に確かめたのが Faraday(Michael Faraday, 1791–1867) で,数式にまとめたのが Maxwell(James Maxwell, 1831–1879) です.速度 v で移動する q クーロンの電荷に働く力は F = q(E + v× B) で表されます.ここで× は外積を表します. 電荷が移動するということは電流が流れることになります.電荷が連続的 な場合には単位長さあたりの電荷密度を ρ とすると 1 時刻に単位面積を通過 する電荷の総量は ρv です.これは単位面積を通過する電流 j になりますの で,電流密度です.これで電流が流れている場合にも力を求めることができ ます. 上の式から電場と磁場がわかれば力がわかり,それから運動方程式を適用 すれば運動が記述できることになります.それで,必要なのは電場と磁場の 間に成り立つ式を考えればいいことになります.これらは以下の式にまとめ られます.
1. div E = ερ 0 2. rot E =−∂∂tB 3. div B = 0 4. c2rot B = ∂E ∂t + j ε0 これが電磁気学のすべてといってもいいそうです.ここで ε0は定数です. ∇ = ∂ ∂x ∂ ∂y ∂ ∂z でナブラといいます.· は内積を表し,ナブラを用いると発散 div は div f (x, y, z) g(x, y, z) h(x, y, z) = ∇ · f (x, y, z) g(x, y, z) h(x, y, z) = ( ∂f ∂x+ ∂g ∂y + ∂h ∂z ) (x, y, z) と表せます.また× は外積を表し,ナブラを用いると回転 rot は rot f (x, y, z) g(x, y, z) h(x, y, z) = ∇ × f (x, y, z) g(x, y, z) h(x, y, z) = ∂h ∂y − ∂g ∂z ∂f ∂z − ∂g ∂x ∂g ∂x− ∂f ∂y (x, y, z) と表せます. 同じように関数 f (x, y, z) について勾配 grad f (x, y, z) =∇f(x, y, z) = ∂f ∂x ∂f ∂y ∂f ∂z (x, y, z) はグラディエントと読みます. 発散,回転,勾配と言われるには当然理由があるのですが,ここではそれ については述べません. 上の式の解説を試みましょう.電荷がまったく存在しないところにも電場 は存在します.電荷がまったく存在しない領域を囲む領域 D を考えると,D の表面 ∂D の上全体を考えると入ってくる電場と出て行く電場は釣り合って いるはずです.もし,電荷が中に存在していればその値が求まるでしょう.こ れを表したのが div E = ερ 0 です.磁場では単位磁化というのが存在しないの で,常に 0 になります.それを表したのが div B = 0 です.電場は磁場に影 響し,磁場は電場に影響することを表したのが残りの式です. 具体的には,ガウスの定理より ∫ D div E dxdydz = ∫ ∂D E· n dS
ここで n は ∂D の微小面積 dS の外側向きの単位法線ベクトルを表します. 左辺は電磁場の方程式より ∫ D ρ ε0 dxdydz ですから D 内の全電荷を ε0で割ったものです.右辺は電場の領域 D への出 入りを表面全体について足したものを表していることがわかります. 同様にストークスの定理より,2 次元の領域 S の縁を左回りにする曲線を Cとすると ∫ S rot E· n dS = ∫ C E· ds が成り立ちます.ここで s は C を左回りにまわる単位接線ベクトル表します. 電場の方程式より左辺は ∫ S −∂B ∂t · n dS 右辺は電場が境界で接線方向にむいている量の総和です.S に垂直な磁場の 時間変化が C の境界の電場を与えていることになります.同様に ∫ S c2rot B· n dS = ∫ S ∂E ∂t · n dS + ∫ S j ε0 · n dS です.したがって,C の境界での磁場は S を垂直に通る電場の変化と電流に よって与えられることになります. 重要なことは真空中の静電磁場の場合です.電荷がないのですから 1. div E = 0 2. rot E =−∂∂tB 3. div B = 0 4. c2rot B = ∂E ∂t となります.前の考察から動く電場は磁場を作り,動く磁場は電場を作るの で真空中を伝わっていくことになります.これが電磁波です.電磁波の方程 式を考えましょう.(4) を微分して c2rot∂B ∂t = ∂2E ∂t2 左辺は
−c2rot rot E =−c2grad div E + c2∆E = c2∆E
を得ます.したがって,
∂2E
∂t2 = c 2∆E
は波動方程式と呼ばれる波の方程式です.もちろん磁場Bも同じ方程式をみ たします.ここで ∆ = ∂ 2 ∂x2 + ∂2 ∂y2 + ∂2 ∂z2 でラプラシアンといいます.ここで用いた
rot rot = grad div−∆ div rot = 0 は定義に基づけば容易に確かめられます. この方程式の解は速度 c をもつ波,例えば E = sin(x + ct) sin(y + ct) sin(z + ct) になります.このことはよく考えてみると不思議です.電磁波は真空中では 速度が一定なのです.速度は相対的なものですから,すれ違う電磁波からお 互いをみれば 2 倍の速度になるはずです.この考察の矛盾をなくすために生 まれたのが相対性理論です.