RSA FA FA AND Booth FA FA RSA 3 4 5

特別研究報告書

題 目

冗長二進数を用いた

RSA 用乗算器の高速化

High-Speed Multiplication for RSA Code

using Redundant Binary System

指 導 教 員

矢野 政顕 教授

報 告 者

学籍番号：

1065085

氏名： 松村 暢也

平成

16 年 2 月 16 日

高知工科大学

電子・光システム工学コ−ス

内容梗概

本論文は著者が高知工科大学大学院工学研究コース修士課程在学中に行って きた冗長二進数を用いたRSA 用乗算器の高速化に関する研究成果をまとめたも のである。 情報をやりとりする通信の分野では、いかにして情報を伝達するか、また情 報の重要度によっては、いかにして送信者、受信者以外の第三者から情報を守 るかといったことが研究され続けている。このことは、高度情報化社会いわれ る現在の社会で、いかに情報に価値があるかということを物語っている。情報 の価値が高くなったことで、一般の生活にまで暗号化技術が浸透している。暗 号は情報の秘匿と認証に用いられている。暗号を用いる認証の例には電子署名 がある。このようにさまざまな面で活用されている暗号には、大きく分けて二 つの種類がある。一つは共通の鍵を使用して暗号化、復号化を行う「共通鍵暗 号」、もう一つは秘密鍵と公開鍵という二種類の鍵を用いる「公開鍵暗号」であ る。公開鍵暗号を用いた方が鍵数を少なくできるため、現在、通信等では公開 鍵暗号が広く用いられている。 しかし、公開鍵暗号は暗号化する際に複雑な演算を行わなければならない。 そのため、通信などで暗号化が用いられるためには高速な処理が必要となる。 そこで、本論文では乗算剰余演算を高速に行うための回路として冗長二進数を 用いた乗算器を提案する。そして、FA を用いた二種類の乗算器との演算時間と ゲート数の比較を行った。比較を行った結果、演算速度については入力のビッ ト数が増加した場合、冗長二進数を用いた乗算器がFA を用いたものより高速で あり、入力ビット数増加による演算時間の増加率も小さいという結果が得られ た。また、部分積生成にあたる AND 回路に Booth デコーダを適用することで 更に高速化が期待できる。しかし、ゲート数に関しては冗長二進数を用いた乗 算器がFA を用いたものと比べて三倍程度増加した。これは、FA の入力ビット 数に対して冗長二進加算器の入力ビット数が二倍になることに関係し、そのた め回路規模が大きくなってしまう。今後の課題としては、冗長二進数を用いた 乗算器の高速性を維持しつつ回路規模を低減させることである。 本論文の第1 章では研究の背景、目的について述べ、第 2 章では RSA 暗号の 演算方法と従来の乗算方法について説明する。第 3 章では冗長二進数を用いた 乗算器について提案する。第 4 章では従来手法の乗算器と提案手法の乗算器に ついて演算速度と面積についての比較・検討結果について述べる。最後に第 5 章では本研究で得られた成果を要約し、今後に残された課題について述べ、結 論とする。 なお、本研究は東京大学大規模集積システム設計教育研究センターを通し、 シノプシス株式会社の協力で行われたものである。

This paper summarizes High-Speed Multiplication for RSA Code using Redundant Binary System, which is performed for the degree of Master at the Graduate School of Engineering, the Kochi University of Technology.

In the communication field, many researches have been carried out into encryption, which is used to protect communication from unauthorized transmitter and receiver. This means that the information becomes more and more valuable in modern society; so-called an advanced information society. The encryption technology becomes popular in a daily life because the value of information is recognized higher and higher. Cipher is used for information secrecy and authentication. The electronic signature is one example of authentication using cipher. The cipher is classified into two types. The one is common key cryptography, which perfumes encryption and decryption using a common key. The other is public key cryptography, which uses two keys; a secret key and a public key. Recently, the public key cryptography is used in communication area, because of its small number of keys comparing to the common key cryptography.

The public key cryptography, however, requires complicated arithmetic operation for encryption and decryption. Therefore, high speed arithmetic processing is necessary in transmitters and receivers’. This paper proposes a multiplier using Redundant Binary System (RBS) as a circuit that performs index and surplus calculations at high speed. We compared the multiplier using RBS with two kinds of multipliers using Full-Adder (FA), with regard to data arrival time and gate count. As for data arrival time, the multiplier using RBS is faster than the multipliers using FA, and this tendency is grown when the number of input data bits is increased. Improvement in the speed is expected when Booth decoder is applied to the partial product generation. As for gate count, the multiplier using RBS requires more gates than the multipliers using FA. Future researches should focus on the reduction of gate count.

This paper consists of 5 Chapters. The first Chapter describes background and purpose of this research. Chapter 2 explains the arithmetic operation method of RSA code comparing with ordinary ones. In Chapter 3, we propose the multiplier using RBS, and Chapter4 shows the comparison results of multipliers regarding to data arrival time and gate count. Finally, Chapter 5 summarizes this paper suggesting future research subjects.

This work is supported by VLSI Design and Education Center (VDEC), the University of Tokyo in collaboration with Rohm Corporation and Synopsys, Inc.

目次

第

1章 はじめに・・・・・・・・・・・・・・・・・・1

1・1 研究背景

・・・・・・・・・・・・・・・・・・・

1

1・2 研究目的

・・・・・・・・・・・・・・・・・・・

2

第

2章 RSA 暗号と乗算回路・・・・・・・・・・・・・3

2・1 RSA 暗号

・・・・・・・・・・・・・・・・・・・

3

2・2 モンゴメリ乗算

・・・・・・・・・・・・・・・・

5

2・3 右向き k−ary 法

・・・・・・・・・・・・・・・・

7

2・4 乗算器

・・・・・・・・・・・・・・・・・・・・

8

第

3章 「冗長二進加算器」を用いた高速乗算回路・ ・ 17

3・1 桁上げの伝播がない加算器とは

・・・・・・・・・・

17

3・2 冗長二進法を用いた加算器

・・・・・・・・・・・

17

3・3 冗長二進加算器を用いた乗算器の設計

・・・・・・・

24

第

4章 各種乗算器の比較・検討・ ・ ・ ・ ・ ・ ・ ・ ・ 27

第

5章 おわりに・・・・・・・・・・・・・・・・・36

謝辞・・・・・・・・・・・・・・・・・・・・・・・・

37

参考文献・・・・・・・・・・・・・・・・・・・・・・

38

付録・・・・・・・・・・・・・・・・・・・・・・・・

39

第

1 章 はじめに

1・1 研究背景

情報をやりとりする通信の世界では、いかにして情報を伝達するか、また情 報の重要度によっては、いかにして送信者、受信者以外の第三者から情報を守 るかといったことが研究され続けている。このことは、高度情報化社会といわ れる現在の社会で、いかに情報に価値があるかということを物語っている。情 報の価値が高くなったことで、一般の生活にまで情報を守るための暗号化技術 が浸透している。現在、暗号は戦争という暗いイメージの中だけではなく、我々 の生活で欠かすことのできない技術なのである。この場合の暗号は情報の秘匿 を目的としている。 また一方、国際的なスケールで実印・印鑑登録証明システムのサイバー世界 版が構築され、その制度化が進んでいる。これは、電子署名とその電子認証シ ステムを暗号によって行うというものである。これは暗号を使うものの一例で あ る が 、 こ の 他 に 、 交 通 や 物 流 の 分 野 で は 自 動 料 金 収 受 シ ス テ ム( Ｅ Ｔ Ｃ:Electronic Toll Collection System)、また医療関係では電子カルテなどがある。 この場合の暗号は認証に使われている。 このようにさまざまな面で活用されている暗号には、大きく分けて二つの種 類がある。一つは共通の鍵を使用して暗号化、復号化を行う「共通鍵暗号」、も う一つは秘密鍵と公開鍵という二種類の鍵を用いる「公開鍵暗号」である。こ の二種類の暗号では最低限必要な鍵の数が違ってくる。具体的に言うと共通鍵 暗 号 で は 通 信 者 の 数 を n と し た と き 最 低 限 必 要 な 鍵 数 kmin は kmin＝ (n-1)+(n-2)+(n-3)+…+1 個となる。同じように公開鍵暗号の場合は kmin=2×n 個 となる。つまり、インターネットなど不特定多数の人が用いる場合の暗号化に は公開鍵暗号を用いたほうが鍵数を少なくできる利点がある。このため現在、 通信等で用いられる暗号には公開鍵暗号が用いられている。

1・2 研究目的

1.1 で述べたように、さまざまな面で暗号の活躍はめざましいものがある。し かし、公開鍵暗号は暗号化する際に共通鍵暗号と比べて複雑な演算を行わなけ ればならない。そのため、通信などで暗号化が用いられるためには高速な処理 が必要となる。そこで、本論文では公開鍵暗号の中でも主流である、RSA 暗号 について、そこで用いられている乗算剰余演算の高速化回路を提案する。 まず、第2 章では RSA 暗号の演算手法と従来の乗算手法について説明し、第 3 章以降では提案手法である冗長二進数を用いた乗算器について説明する。また、 第４章では従来手法の乗算器と提案手法の乗算器の演算速度と面積について比 較検討する。第5 章では本研究についてまとめる。

第

2 章 RSA 暗号と乗算回路

2・1 RSA 暗号

RSA 暗号とは、1977 年に MIT(マサチューセッツ工科大学)のリベスト (Rivest)、シャーミル(Shamir)、アドルマン(Adleman)のグループが発表した暗 号化方式である。この暗号は素因数分解の難しさを利用したもので、素数の性 質をうまく活用している。RSA 暗号では、送信者は公開鍵で暗号化し、暗号化 された文書を受け取った受信者は秘密鍵を用いて復号化する。その関係を図2.1 で簡単に示す。 の秘密鍵 の公開鍵 の公開鍵 の秘密鍵 各受信者の公開 鍵で暗号化 各受信者自身の 秘密鍵で復号化 受信者B 暗号文b 受信者B 平文 受信者C 受信者C 平文 暗号文c 送信者A 平文 受信者D の公開鍵 受信者D の秘密鍵 暗号文d 平文 図2.1 公開鍵暗号の仕組み この公開鍵はインターネットのホームページ上などに公開しておき、秘密鍵 は自分以外に知られないようにしておく。

RSA 暗号化の演算には次のような数学的定義が存在する。 a,b を整数とし、n を正の整数とする。このとき、n

(

a− ならば a は b に nb

)

を法として合同と言い、

(

n b a ≡ mod

)

)

)

(2・1) と記述する。 RSA 暗号では式(2・1)の定義を踏まえて次の定理が重要となる。 ●オイラーの定理 (a,n)=1 ならば ( )

₍

_n aφ n ≡ 1 mod (2・2) となる。ここで、

φ

( )

n はオイラー関数と呼ばれ、

( ) (

n = p −1

) (

⋅ q −1

)

φ

(2・3) と表される。このp と q は互いに異なる素数で、p と q の積が n である。 ●フェルマーの定理 P を素数とすれば、全ての a に対して

(

P a aP ≡ mod (2・4) a P でなければ、 ( )

₍

_P a P−1 ≡ 1 mod

)

)

)

(2・5) となる。 これらの考え方を用いてRSA 暗号化の数学的手法は次のようになる。

(

M C Pe = _mod (2・6) このとき、 は平文、 は公開鍵、 は暗号文、 は法の値で公開鍵とな る。例えば、 =5、 =3、 =33 とすると、 P P e C M e M

(

mod 33 26 125 53 = = (2・7) となる。つまり暗号文 C は 26 となる。

逆に、復号化する場合も式(2・6)を用いて、

(

M P Ce′ = _mod

)

)

)

(2・8) と表せる。このとき、 は秘密鍵である。 =7 として前述の暗号文 =26 を 復号化してみると、 e ′ e ′ C

(

mod33 5 8031810176 267 = = (2・9) というふうに平文 の値5 が得られる。これは、 =33 より(P,M)=1、オイラ ー関数 =20 となるため、 P M

( )

n

φ

( )

( )

₍

₎

33 mod 1 1 20 21 7 3 P P P P P P P = = + = φ n ⋅ = ⋅ = (2・10) となるからである。 式(2・6) 、式(2・8)を見てもわかるように、RSA 暗号のような公開鍵暗号は、 送信側も受信側も同じ装置で通信できるので、装置のコストを下げやすい。ま た、第１章で述べたように共通鍵暗号に比べて公開鍵暗号は鍵の数を抑えるこ とができる。その為、公開鍵暗号は、通信の分野で最も広く使われているもの である。 しかし、式(2・6)や式(2・8)のような乗算剰余演算は、通信等で用いられるこ とからも高速性が要求される。この乗算剰余演算を高速に行うために、モンゴ メリ乗算や右向き k-ary 法を用いる手法が提案されている[1]。以下でモンゴメ リ乗算、右向きk-ary 法について説明する。

2・2 モンゴメリ乗算

例えば、

(

C AB mod (2・11) を求めるにあたり、 は から を引く操作を繰り返して余りを求め るが、引く回数は の値に依存する。減算の回数は乗算剰余演算のスピード に影響する。そこで、減算の回数を減らす方法としてモンゴメリ乗算が用いら れている。 C mod AB AB C モンゴメリ乗算を行うにあたって

(

C

)

X AR 2 mod = (2・12)

(

C

)

Y B mod = (2・13) を求める。このX ,Y を用いてモンゴメリ乗算

(

C R XY mod

)

(2・14) が行われるが、 R XY が割り切れるとは限らないので、割り切れるような値

(

C R UC XY mod +

₎

)

)

(2・15) のU を決める。このとき、式(2・14)と式(2・15)の解は同値である。また、U の 値は

(

R C XY U = ′ mod (2・16) で求められる。このときの C は ′

(

R C C′ = − −1 mod (2・17) となる値である。 式(2・15)の解をX ′とし、再び

(

C R UC Y X mod + ′ ′

₎

)

)

(2・18) を解く。このとき、Y は1 とする。ここで求められた解が式(2・11)と同値にな る。ここで、 より であり、 ′ Y C , C X < < XY < C2

(

R C C′ = − −1 mod (2・19) より

(

R C C = − ′−1 mod (2・20) で あ る か ら が 成 立 す る 。 よ り と で き る の で 、 となる。つまり、 より R C < CR R C < XY <

CR

C

2

<

C XY < 2 < CR C R XY < となり、よって C R XY 2 < が成立する。このことより、式(2・14)は高々1 回の減算で求めるこ とができる。

2・3 右向き k-ary 法

次に、べき乗演算を高速化する手法として右向き k-ary 法を紹介する。右向 き k-ary 法はべき乗の値を k ビットずつに区切ることで乗算回数を減らすもの である。例として の演算を、通常のべき乗演算で行う右向きバイナリ 法と、右向きk-ary 法で行い、その過程を図 2.2(a),(b)に示す。

(

C A11 mod

)

初期値:1 × × × × × × × A2_{(mod C)}

12_{A(mod C) (A}2₎2_{A(mod C) (A}5₎2_{A(mod C)}

A A

A

(a) 右向きバイナリ法

初期値:A[b1]_=A2 _(A2₎2_{(mod C) (A}4₎2_{(mod C) A}8_A3_{(mod C)}

× × × A3_{(mod C)} A[b0]_=A3_より (b) 右向き k-ary 法 の11 を二進数で示すと“1011”であり、この値を k ビットずつに 区切る。ここでは2 ビットずつに区切り、b1=“10”、b0=“11”とする。

(

C

)

A11 mod 図2.2 右向きバイナリ法と右向き k-ary 法 図2.2 からもわかるように、乗算の回数は、(a)右向きバイナリ法では 7 回、 (b)右向き k-ary 法では 3 回と右向き k-ary 法のほうが少ない。これより、右向 きバイナリ法より右向き k-ary 法が高速に計算できることが分かる。ただし、 右向きk-ary 法では を前計算しておかなければならない。この前計算 はk ビットで区切った場合、2 個の値を用意しなければならない。

(

C A mod3

)

1 − k 右向きk-ary 法に用いられるべき乗演算回数は、



n k



× k (2・21)

ただし、n kが割り切れる場合

( )

{

−1 × n k k

}

(2・22) となる。例えば1024 ビットのべき乗数を 1~1024 の幅で区切った場合のべき乗 演算、つまり乗算の回数の変化を図2.3 に示す。 図2.3 kbit同時演算によるべき乗演算回数(k=1∼1024) 0 200 400 600 800 1000 1200 1 65 129 193 257 321 385 449 513 577 641 705 769 833 897 961 しかし、右向き k-ary 法を用いても入力ビット数が多くなれば乗算回数が多 くなることに変わりない。通常RSA 暗号では 1024 ビット以上の値を用いるた め、右向きk-ary 法のみの適用では高速な RSA 暗号化回路を実現できない。こ のため、回路全体の高速化には乗算器の高速化を行うことが必要となる。

2・4 乗算器

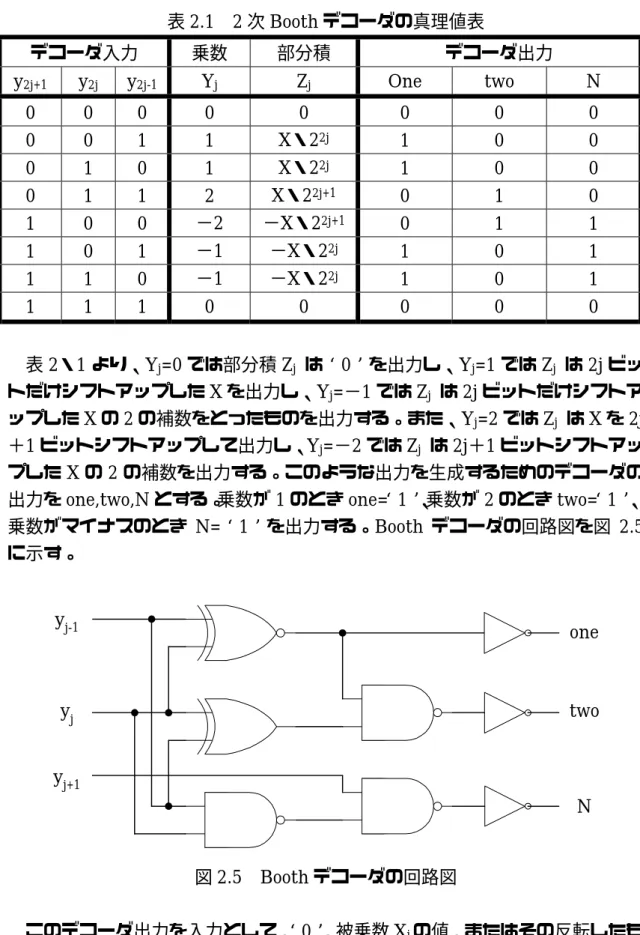
乗算器の構成を図2.4 に示す。

部分積生成 部分積加算 桁上げ信号吸収 被乗数X （Nビット） 乗数Y （Nビット） 積Z （2N−1ビット） 図2.4 乗算器の構成 通常、ハードウェアで乗算器を実現する際、筆算と同じ手法をとる。乗算 器の演算時間は、部分積生成時間と部分積加算時間、ならびに桁上げ信号吸収 での加算時間の和となる。このため、演算時間を削減するためには部分積生成 部や加算部を高速に処理しなければならない。そこで、部分積生成には 2 次 Booth を用い、加算部には Wallace tree、先見桁上げ加算器(Carry Look-ahead Adder:CLA )や 2 進先見桁上げ加算器(Binary Look-ahead Carry Adder:BLCA) を用いて高速な乗算器を実現している[2]。 2 次 Booth は部分積を削減するためのもので、例えば 6 ビット入力の場合、 乗数Y は

(

)

(

)

(

)

(

)

(

0 1 0 1 2 1 2 3 4 3 4 5 0 0 1 1 2 2 3 3 4 4 5 5 0 0 1 1 2 2 3 3 4 4 5 5 2 2 2 2 2 2 2 2 1 2 2 2 1 2 2 2 2 2 2 2 2 2 − + + ⋅ − + + + ⋅ − + ⋅ + + ⋅ − = ⋅ + ⋅ − + ⋅ + ⋅ − + ⋅ + ⋅ − = ⋅ + ⋅ + ⋅ + ⋅ + ⋅ + ⋅ − = y y y y y y y y y y y y y y y y y y y y y Y

)

(2・23) と変形することができる。なお、MSB である[ ]は符号ビットである。乗数の 三つの連続するビットをまとめることで、乗数の数を減らし部分積数を削減す 5 y る。この場合、部分積数を6 から 3 に減らすことができる。このとき、2 次 Booth のデコーダは、表2.1 のような真理値表となる。表中の X は被乗数である。

表2.1 2 次 Booth デコーダの真理値表 デコーダ入力 乗数 部分積 デコーダ出力 y2j+1 y2j y2j-1 Yj Zj One two N 0 0 0 0 0 0 0 0 0 0 1 1 X・22j _{1 0 0} 0 1 0 1 X・22j _{1 0 0} 0 1 1 2 X・22j+1 _{0 1 0} 1 0 0 −2 −X・22j+1 _{0 1 1} 1 0 1 −1 −X・22j _{1 0 1} 1 1 0 −1 −X・22j _{1 0 1} 1 1 1 0 0 0 0 0 表2・1 より、Yj=0 では部分積 Zj は‘0’を出力し、Yj=1 では Zj は 2j ビッ トだけシフトアップしたX を出力し、Yj=−1 では Zj は 2j ビットだけシフトア ップしたX の 2 の補数をとったものを出力する。また、Yj=2 では Zj は X を 2j ＋1 ビットシフトアップして出力し、Yj=−2 では Zj は 2j＋1 ビットシフトアッ プしたX の 2 の補数を出力する。このような出力を生成するためのデコーダの 出力をone,two,N とする。乗数が 1 のとき one=‘1’、乗数が 2 のとき two=‘1’、 乗数がマイナスのとき N=‘1’を出力する。Booth デコーダの回路図を図 2.5 に示す。 y_j-1 y_j y_j+1 one two N 図2.5 Booth デコーダの回路図 このデコーダ出力を入力として、‘0’、被乗数 Xjの値、またはその反転したも

の、1 ビット前の被乗数 Xj-1の値、またはその反転したものを出力するマルチプ レクサを用いることで部分積生成を行う。このマルチプレクサの回路図を図2.6 に示す。 one two N X_j-1 X_j Z_j 図2.6 2 次 Booth に用いられるマルチプレクサの回路図 ここで、MSB である[ ]は符号ビットとしているので、この部分の生成方法 は図2.6 とは別の回路になる。Booth デコーダの出力 one,two のどちらか一方 5 y が‘1’の場合、N が‘0’ならば被乗数の MSB である XN-1を各部分積の符号 ビット ZjNとして出力し、N が‘1’ならば XN-1を反転して出力する。one,two ともに‘0’ならば‘0’を出力する。この符号ビット生成回路を図 2.7 に示す。 X_N-1 one two N Z_jN 図2.7 2 次 Booth に用いられる符号ビット生成回路 図2.5 から図 2.7 までの回路を組み合せたものが、2 次 Booth による部分積生 成回路である。

高速に行うものである。FA は三つの同じ重みの入力を二つの出力にする。この 性質を利用して、入力を 2/3 ずつに減少して 2 値に絞り込んでいく。tree を組 んだ例を図2.8 に示す。 8入力 7入力 6入力 5入力 4入力 図2.8 tree 構成例(4∼8 入力)

このtree で各ビットを 2 値ずつにまとめ、最終段で CLA や BLCA を用いて 部分積の加算を終える。 CLA の例として 4 ビット CLA を取り上げる。 入力をA,B、桁上げを C としたとき各ビットの桁上げ は次のような 式になる。 3 0 C C ∼

(

)

0 1 0 0 0 1 0 0 0 Q C G B A C B A C ⋅ + = ⊕ + ⋅ = − − (2・24)

(

)

1 0 1 1 1 0 1 1 1 Q C G B A C B A C ⋅ + = ⊕ + ⋅ = (2・25)

(

)

2 1 2 2 2 1 2 2 2 Q C G B A C B A C ⋅ + = ⊕ + ⋅ = (2・26)

(

)

3 2 3 3 3 2 3 3 3 Q C G B A C B A C ⋅ + = ⊕ + ⋅ = (2・27) 式(2・24)の C は‘0’であり、 −₁ n n n A B G = ⋅ (2・28) n n n A B Q = ⊕ (2・29) と置いている。ここで、それぞれの桁上げは次段までの入力で表すことができ る。それらの式は式(2・30)から式(2・32)となる。

(

)

1 0 1 1 0 1 1 0 1 0 1 1 Q Q C Q G G Q Q C G G C ⋅ ⋅ + ⋅ + = ⋅ ⋅ + + = − − (2・30)

(

2 1 0 1 2 1 0 2 1 2 2 1 0 1 1 0 1 2 2 Q Q Q C Q Q G Q G G Q Q Q C Q G G G C ⋅ ⋅ ⋅ + ⋅ ⋅ + ⋅ + = ⋅ ⋅ ⋅ + ⋅ + + = − −

)

_(2・31)

(

)

3 2 1 0 1 3 2 1 0 3 2 1 3 2 3 3 2 1 0 1 2 1 0 2 1 2 3 3 Q Q Q Q C Q Q Q G Q Q G Q G G Q Q Q Q C Q Q G Q G G G C ⋅ ⋅ ⋅ ⋅ + ⋅ ⋅ ⋅ + ⋅ ⋅ + ⋅ + = ⋅ ⋅ ⋅ ⋅ + ⋅ ⋅ + ⋅ + + = − − (2・32) これらの式から分かるように、全ての桁上げが入力 A,B のみによって定まる ため、桁上げ伝播に関する遅延を考えなくてもよい。しかし、入力のビット数 が増えるとMSB に近い桁上げの論理式は長くなり、その結果、LSB 側と MSB 側の出力に遅延が生じる。これを避けるため入力ビット数が多い場合、4 ビット ずつに区切って用いるのが一般的である。この場合、入力 4 ビットおきに桁上 げの伝播が発生して伝播遅延のある加算器となる。4 ビット CLA の回路図を図 2.9 に示す。

G₃ C_-1 Q₃ G₂ Q₂ G₁ Q₁ G₀ Q₀ B₀ A₀ B₁ A₁ B₃ A₃ A₂ B₂ S₀ C₀ S₁ S₂ S₃ C₁ C₂ C₃ 図2.9 4 ビット CLA 多ビット入力の加算を行う場合 CLA よりも高速な加算器として BLCA があ る。BLCA は CLA の論理式を見直すことで高速な回路を実現している。 加減算の可能なBLCA を考える。最下位ビットへの下からの桁上げC₋₁を 1 1 2 1 1 1 − − − − − − + ≡ ⋅ + = q g C Q G C (2・33) のように定義する。このとき、加算時の C は ₋₁

(

)

(

)

2 2 2 1 1 1 1 1 0 0 0 0 0 0 − − − − − − − − ⋅ + = ⋅ ⊕ + ⋅ = ⋅ ⊕ + ⋅ = C C C B A B A C (2・34) となり、減算時の C は ₋₁

(

)

(

)

2 2 2 1 1 1 1 1 1 0 0 0 0 0 − − − − − − − − ⋅ + = ⋅ ⊕ + ⋅ = ⋅ ⊕ + ⋅ = C C C B A B A C (2・35) となる。ここで、 C は加算時‘0’、減算時‘1’なので C_{−1 −2} =1となる。 これより、 1 1 1 1 − − − −

≡

≡

Q

q

G

g

(2・36) となる。この式を次のように表す。

(

g −1 , q −1

)

≡

(

G −1 , Q −1

)

)

)

(2・37) 次に C を式(2・33)の C を用いて表すと、 _{0 −1}

(

)

(

0 0 1

)

0 1 1 1 0 0 1 0 0 0 − − − − − ⋅ + ⋅ + ≡ + ⋅ + ≡ ⋅ + = q Q g Q G q g Q G C Q G C (2・38) となり、式(2・33)と同様に、 0 0 0 g q C ≡ + (2・39) と表す。このとき、 1 0 0 1 0 0 0 − −

⋅

≡

⋅

+

≡

q

Q

q

g

Q

G

g

(2・40) である。ここで、二項演算子◎ を用いて次のように表記する。

(

g 0 ,q 0

)

≡

(

G 0 ,Q 0

)

◎

(

G −1,Q −1 (2・41) このようにしてn ビット目の式を求めると、

(

gn,qn

) (

≡ Gn,Qn

) (

◎Gn−1,Qn−1

)

◎・・・◎

(

G0,Q0

) (

◎Gn−1,Qn−1 (2・42) となり、各ビットのG,Q の値から各ビットの桁上げ信号が得られる。しかし、 式(2・42)のままでは各ビットの g,q の値は伝播し、n ビット目への桁上げ生成 にはn-1 段の二項演算子を行うセルが必要となる。そこで tree 状の構成をとっ てセルの段数を減らす。そのtree を図 2.10 に示す。

(G_-1,Q_-1) (G₀,Q₀) (G₁,Q₁) (G₂,Q₂) (G₃,Q₃) (G₄,Q₄) (G₅,Q₅) (G₆,Q₆) (G₇,Q₇) (g_-1,q_-1) (g₀,q₀) (g₁,q₁) (g₂,q₂) (g₃,q₃) (g₄,q₄) (g₅,q₅) (g₆,q₆) (g₇,q₇) 図2.10 二項演算子を行うセルの tree 構造 例として、16 ビットの BLCA を図 2.11 に示す。図中の R はレジスタ、 QG,PB,NB は二項演算子を行うセルであり、SM は前段の桁上げと中間和を加 えるためのXOR 回路である。 R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R QG QG QG QG QG QG QG QG QG QG QG QG QG QG QG QG PB PB PB PB PB PB PB PB PB PB PB PB PB PB PB PB PB PB PB PB PB PB PB PB PB PB PB PB PB PB PB PB NB NB NB NB NB NB NB NB NB NB NB NB NB NB NB NB NB NB NB NB NB NB NB NB NB NB NB NB NB NB NB NB B15A15 B14A14 B13A13 B12A12 B11A11 B10A10 B9 A9 B8 A8 B7 A7 B6 A6 B5 A5 B4 A4 B3 A3 B2 A2 B1 A1 B0 A0 SM SM SM SM SM SM SM SM SM SM SM SM SM SM SM SM S15 S14 S13 S12 S11 S10 S9 S8 S7 S6 S5 S4 S3 S2 S1 S0 NC-1 =1 Ng-1 =1 q-1 =1 図2.11 16 ビット BLCA

第

3 章

「冗長二進加算器」を用いた高速乗算回路

3・1 桁上げの伝播がない加算器とは

第2 章で示した乗算器では加算器として FA を用いているため、桁上げが伝播 する。その為、ビット数が増加した場合、桁上げ伝搬時間が増加し、乗算器の 演算時間が大きくなる。RSA 暗号では 1024 ビット以上の入力が用いられるた め、これまでに示した乗算器では桁上げの伝播遅延により高速性を期待できな い。桁上げ伝播の影響がない加算手法である冗長二進法(Redundant Binary System)を用いた加算は乗算器の高速化に寄与すると考えられる。ここでは、冗 長二進法を用いた加算器について説明する。

3・2 冗長二進法を用いた加算器

冗長二進法とは、通常の二進数に‘−1’を加えた数体系である[3]。‘−1’の 値を用いることで加算時の桁上げ伝播を防ぎ、高速な加算器を作ることができ る。二進数で加算した場合と冗長二進数で加算した場合のモデルとして7＋1 の 計算を行ったものを図3.1 に示す。

0 1 1 1

0 0 0 1

+

0 1 1 0

0 0 0 1

0 1 0 0

0 0 1

0 0 0 0

0 1

1 0 0 0

中 間 和 桁 上 げ 中 間 和 桁 上 げ 中 間 和 桁 上 げ 和

1 0 0 - 1

0 0 0 1

+

1 0 0 0

和 (a) 二進数の加算 (b) 冗長二進数の加算 図3.1 二進数の加算と冗長二進数の加算モデル

冗長二進数の場合、十進数の7 を“100-1”で表しているが、“1-111”や“10-11” も十進数の7 を意味し、表し方は一通りではない。 図3.1 に示すように、二進数の加算では桁上げが伝播しているが、冗長二進数 の加算では桁上げの伝播がなく二進数の加算よりも高速に演算結果が得られる。 ただし、冗長二進数をハードウェアで実現する際、冗長二進数の‘0’,‘1’, ‘−1’はそれぞれ 2 ビットの二進数“00”,“01”,“10”に対応づける。その 際、“11”を‘0’として考える。 入力をA,B とし、桁上げを C、中間和を ss、和を S とする。このとき、i ビ ット目の中間和ssiとi ビット目の桁上げ Ciは、i ビット目の入力 Ai,Biとi-1 ビ ット目の入力Ai-1と Bi-1から求められ、i ビット目の和 Siは、i ビット目の中間 和ssiとi-1 ビット目の桁上げ Ci-1との加算により求められる。この加算器の真 理値表を表3.1 に示す。 表3.1 冗長二進加算器の真理値表(1) 入力ビット 前段の入力ビット 中間和 桁上げ Ai(1) Ai(0) Bi(1) Bi(0) Ai-1(1) Ai-1(0) Bi-1(1) Bi-1(0) ssi(1) ssi(0) Ci(1) Ci(0)

0 0 0 0 1 1 1 1 0 1 1 0 1 0 0 1 ‐ ‐ _{0 0 0 0} 0 0 0 1 1 1 0 1 1 0 を含む 0 1 0 0 0 1 0 0 0 1 1 1 1 0 を含まない 1 0 0 1 0 0 1 0 1 1 1 0 1 0 を含む 0 1 1 0 1 0 0 0 1 0 1 1 1 0 を含まない 1 0 0 0 0 1 0 1 ‐ ‐ 0 0 0 1 1 0 1 0 ‐ ‐ 0 0 1 0 表3.1 から各出力の論理式を求めると次のようになる。

(

) (

{

⊕ ⊕ ⊕

)}

⋅α = _{(1) (0) (1) (0)} ) 1 ( i i i i i A A B B ss (3・1)

(

) (

)

{

⊕ ⊕ ⊕

}

⋅α = _{(1) (0) (1) (0)} ) 0 ( i i i i i A A B B ss (3・2)

(

)

(

)

{

⊕ ⋅ ⋅ + ⋅ ⋅ ⊕

}

⋅α + ⋅ ⋅ ⋅ = _{(1) (0) (1) (0) (1) (0) (1) (0) (1) (0) (1) (0)} ) 1 ( i i i i i i i i i i i i i A A B B A A B B A A B B C (3・3)

(

)

(

)

{

⊕ ⋅ ⋅ + ⋅ ⋅ ⊕

}

⋅α + ⋅ ⋅ ⋅ = _{(1) (0) (1) (0) (1) (0) (1) (0) (1) (0) (1) (0)} ) 0 ( i i i i i i i i i i i i i A A B B A A B B A A B B C (3・4) このとき、 ) 0 ( 1 ) 1 ( 1 ) 0 ( 1 ) 1 ( 1 − − − − ⋅ + ⋅ = A_i A_i B_i B_i α (3・5) 次に、中間和と桁上げから和を求める真理値表を表3.2 に示す。 表3.2 冗長二進加算器の真理値表(2) 中間和 前段の桁上げ 和 ssi(1) ssi(0) Ci-1(1) Ci-1(0) Si(1) Si(0)

0 0 0 0 0 1 0 1 0 0 1 0 1 0 0 0 0 1 0 1 × × 0 1 1 0 1 1 0 0 1 0 0 1 1 1 1 0 1 0 × × 表3・2 中の×は起こりえない入力の組合せに対する出力である。この場合の 出力をdon’t care として、表 3.2 より式を求めると、 ) 1 ( 1 ) 1 ( ) 1 (

=

i

⊕

i− i

ss

C

S

(3・6) ) 0 ( 1 ) 0 ( ) 0 (

=

i

⊕

i− i

ss

C

S

(3・7) となる。この式(3・1)から式(3・7)までを用いて設計した回路を図 3.2 に示す。

A1(

1

)

B1(0)

A1(

0

)

B1(1)

A0(

1

)

B0(0)

A0(

0

)

B0(1)

ss(1) ss(0) C(1) C(0)

C-(1)

C-(0)

S(1) S(0)

S(1)

C(0)

C(1)

S(0)

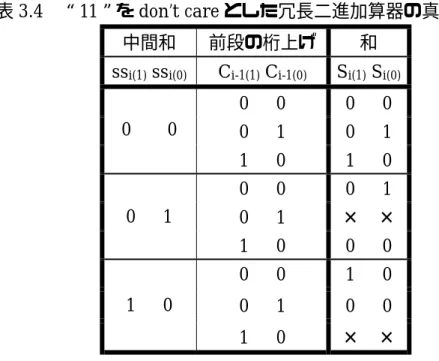
図3.2 冗長二進加算器(1) この回路では“11”という信号を用いているが、‘0’を表すのには“00”が あるので“11”を don’t care として回路の簡単化を図った。その真理値表を表 3.3 に示す。

表3.3 “11”を don’t care とした冗長二進加算器の真理値表(1)

入力ビット 前段の入力ビット 中間和 桁上げ Ai(1) Ai(0) Bi(1) Bi(0) Ai-1(1) Bi-1(1) ssi(1) ssi(0) Ci(1) Ci(0)

0 0 0 0 0 1 1 0 1 0 0 1 ‐ ‐ 0 0 0 0 0 0 0 1 1 を含む 0 1 0 0 0 1 0 0 1 を含まない 1 0 0 1 0 0 1 0 1 を含む 0 1 1 0 1 0 0 0 1 を含まない 1 0 0 0 0 1 0 1 ‐ ‐ 0 0 0 1 1 0 1 0 ‐ ‐ _{0 0 1 0} 入力の“11”を don’t care としているので、前段の入力は Ai-1(1)とBi-1(1)のみ

見ればよい。表3.3 から式を求めると次のようになる。 α ⋅ ⋅ ⋅ + ⋅ ⋅ + ⋅ ⋅ + ⋅ ⋅ =( (1) (0) (0) (1) (0) (1) (0) (1) (0) (1) (1) (0)) ) 1 ( i i i i i i i i i i i i i A A B A A B A B B A B B ss (3・8) α ⋅ ⋅ ⋅ + ⋅ ⋅ + ⋅ ⋅ + ⋅ ⋅ =( (1) (0) (0) (1) (0) (1) (0) (1) (0) (1) (1) (0)) ) 0 ( i i i i i i i i i i i i i A A B A A B A B B A B B ss (3・9) α ⋅ ⋅ + ⋅ + ⋅ = _{(1) (1)} ( _{(0) (1) (1) (0)}) ) 1 ( i i i i i i i A B A B A B C (3・10) α ⋅ ⋅ + ⋅ + ⋅ = _{(0) (0)} ( _{(1) (0) (0) (1)}) ) 0 ( i i i i i i i A B A B A B C (3・11) このとき、 ) 1 ( 1 ) 1 ( 1 − − + = A_i B_i α (3・12) である。 次に、中間和と前段の桁上げ、そして和の関係を示した真理値表を表3.4 に示 す。

表3.4 “11”を don’t care とした冗長二進加算器の真理値表(2) 中間和 前段の桁上げ 和

ssi(1) ssi(0) Ci-1(1) Ci-1(0) Si(1) Si(0)

0 0 0 0 0 1 0 1 0 0 1 0 1 0 0 0 0 1 0 1 × × 0 1 1 0 0 0 0 0 1 0 0 1 0 0 1 0 1 0 × × 表3・4 中の×は起こりえない入力の組合せに対する出力である。この場合の 出力をdon’t care とすると、式は次のようになる。 ) 0 ( 1 ) 1 ( ) 1 ( 1 ) 0 ( ) 1 (

=

i

⋅

i−

+

i

⋅

i− i

ss

C

ss

C

S

(3・13) ) 1 ( 1 ) 0 ( ) 0 ( 1 ) 1 ( ) 0 ( = i ⋅ i− + i ⋅ i− i ss C ss C S (3・14) 式(3・8)から式(3・14)までを用いて設計した冗長二進加算器の回路を図 3.3 に示す。 この回路図からも分かるように、桁上げは次段の桁上げに影響を及ぼしてい ないので、並列に冗長二進加算器を並べても加算器間での遅延時間は伝播しな い。そのことを示したグラフを図3.4 に示す。図 3.4 は入力が 16,32,64 ビット の CLA、BLCA、冗長二進加算器の演算時間を比較したものである。冗長二進 加算器は入力ビット数にかかわらず一定の演算時間であるから、この演算時間 を 1 として各加算器の演算時間を相対値で表した。入力ビット数が増加すれば CLA も BLCA も演算時間が増加するため、多ビットの加算を行う場合、冗長二 進加算器のほうが高速な加算器となることが分かる[4]。続いて、3・3 節では冗 長二進加算器を用いた乗算器の設計を行う。

A_j-1(1) B_j-1(1) A_j(1) A_j(0) B_j(1) B_j(0) ss_j(1) ss_j(0) C_j(1) C_j(0) C_j-1(1) C_j-1(0) S_j(1) S_j(0) 図3.3 冗長二進加算器(2) 0 1 2 3 4 5 6 7

16bit 32bit 64bit ビット数(bit)

演算時間の比

RCA BLCA 冗長二進加算

3・3 冗長二進加算器を用いた乗算器の設計

冗長二進加算器を用いた乗算器のブロック図を、図3.5 に示す。 部 分 積 生 成 (A N D 回 路 ) 部 分 積 加 算 ( 冗 長 二 進 加 算 セ ル ) 被 乗 数X (N ビ ッ ト ) 乗 数Y (N ビ ッ ト ) 積Z (2 N -1 ビ ッ ト ) 図3.5 冗長二進加算器を用いた乗算器のブロック図 部分積生成にはAND 回路を用い、入出力は冗長二進数の状態で行う。なお、 二進数を冗長二進数に変換する際には、二進数の各ビットに‘0’を拡張すれば よい。一方、冗長二進数を二進数に変換する場合は、奇数ビット目と偶数ビッ ト目を分けて奇数ビットの集まりから偶数ビットの集まりを減算すればよい。 乗算自体は冗長二進数のまま実行できるので、二進数への変換は最後の積を得 るときに行えばよい。 部分積加算に用いている冗長二進加算セルは、図3.3 で示した冗長二進数加算 器をFA と同じように tree 状に構成している。例として 6 ビット乗算における 部分積加算のブロック図を図3.6 に示す。

X₀Y₁X₁Y₀ X₁Y₁X₂Y₀ X₃Y₁X₄Y₀ X₂Y₁ X₅Y₁0 X₄Y₁X₅Y₀ X0Y2 X₃Y₀ X0Y3X1Y2 X1Y3X2Y2 X3Y3X4Y2 X2Y3 X5Y3 0 X4Y3X5Y2 X3Y2 0 0 X0Y5X1Y4 X1Y5X2Y4 X3Y5X4Y4 X2Y5 X5Y5 0 X4Y5X5Y4 X3Y4 X0Y4 0 Z₁ Z₂ Z₃ Z₄ Z₅ Z₆ Z₇ Z₈ Z₉ Z₁₀ Z₁₁ X₀Y₀ Z₀ 図3.6 6 ビット乗算器の部分積加算部 この乗算器では冗長二進数を用いているので、FA を用いた二進数の乗算器と 比べ、回路規模や、消費電力が大きくなるが、ビット数の増加に伴う部分積加 算の段数の増加は少ない。この様子を図3.7 に示す。 0 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 _{10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63} n(個) 段数(段) 冗長二進加算器 FA 図3.7 n 個同時加算時の加算器段数 部分積加算の段数は、部分積生成時に同じ重みの値が最大でいくつあるかで

きまる。具体的にはn ビットの入力に対する AND 回路での部分積生成では最大 でn 個の同じ重みの値が出力されることになり、2 次 Booth を用いた場合では 最大で(n/2)+1 個出力される。加算器の段数はこの値から、FA の場合 3 入力が 2 出力となるので、

( ) ( )

1

3

2

2

×

≤

i

n

_(3・15) を満たす の値が段数となる。一方、冗長二進加算器では2 入力が 1 出力となる ので、

i

( )

1

2

1

_≤

×

i

n

(3・16) を満たす の値が段数となる。

i

第

4 章 各種乗算器の比較・検討

RSA 暗号用の高速乗算器を設計するにあたり、第 2 章、第 3 章で示した乗算 器がどの程度の性能を持つかを調べるために比較・検討を行った。

比較対象の乗算器は

・ Wallace tree, CLA を用いた乗算器（図 4.1(a)）

・ 2 次 Booth, Wallace tree, BLCA を用いた乗算器（図 4.1(b)） ・ 冗長二進加算器を用いた乗算器（図4.1(c)） の三種類で、各6,8,16 ビットの回路とした。それぞれの回路のブロック図を図 4.1 に示す。 部分積生成(AND回路) 桁上げ信号吸収(CLA) 部分積生成(2次Booth) 桁上げ信号吸収(BLCA) 部分積加算、桁上げ信号吸収 （冗長二進加算器） 部分積加算（Wallace tree） 部分積生成(AND回路) 部分積加算（Wallace tree） (a) (b) (c) 図4.1 比較対象となる乗算器のブロック図 比較項目は演算時間とゲート数である。比較の対象となる回路はVHDL で設 計し(各 6 ビット乗算器の VHDL ソースコードは付録を参照)、Synopsys 社の design analyzer を使用して論理合成、最適化を行い、それぞれの回路に対する 演算時間、ゲート数のデータを出力した。なお、library には rohm035_h を用 いた。 論理合成した回路として、6 ビットのものと 8 ビットのものを図 4.2(a),(b),(c) に示す。回路図中の太線がクリティカルパスを示している。

各乗算器の演算時間、ゲート数の算出結果を表4.1 に示す。 表4.1 各回路のゲート数、演算時間の算出結果 Bit Circuit The number of Gate

[gate]

Data arrival time [ns] (a) 169 6.36 (b) 126 5.55 6 (c) 661 6.23 (a) 377 9.04 (b) 240 7.23 8 (c) 1215 6.38 (a) 1612 14.48 (b) 1087 11.54 16 (c) 5123 8.61 表4.1 中の Circuit(a),(b),(c)は図 4.1 で示したようにそれぞれ、Wallace tree, CLA を用いた乗算器、2 次 Booth, Wallace tree, BLCA を用いた乗算器、冗長 二進加算器を用いた乗算器である。

表4.1 から分かるように、演算時間の最も短い乗算器は冗長二進加算器を用い た乗算器である。しかし、通常の乗算器と違い各ビットが倍の長さを持つため、 ゲート数は大幅に増加する。表 4.1 の演算時間をグラフで表したものが図 4.3、 ゲート数をグラフで表したものが図4.4 である。

0 1000 2000 3000 4000 5000 6000 bit数 (bit)

The number of Gate (gate)

(a) (b) (c) 16bit 8bit 6bit 図4.3 各乗算器の演算時間 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 bit数 (bit)

Data arrival time (ns)

(a) (b) (c) 8bit 16bit 6bit 図4.4 各乗算器のゲート数

図4.3 より、2 次 Booth, Wallace tree, BLCA を用いた乗算器と冗長二進加算 器を用いた乗算器の比較では8 ビット、16 ビットそれぞれの回路で冗長二進加 算器を用いた乗算器のほうが高速であるが、ビット数が増えた場合の演算時間 の増加率は冗長二進加算器を用いた乗算器のほうが小さい。よって、多ビット の入力の場合、高速性を求めるのであれば冗長二進加算器を用いた乗算器の回 路が有効であるといえる。

第

5 章 おわりに

著者が提案した冗長二進加算器を用いた乗算器は、従来のFA を用いた乗算器 より高速であり、入力ビット数増加による演算時間の増加率が小さい回路であ るという結果が得られた。また、冗長二進加算器を用いた乗算器の部分積生成 回路である AND 回路に Booth デコーダを適用することで更なる高速化が期待 できる。 しかし、冗長二進数を用いた乗算器では、FA を用いた乗算器と比べて入力ビ ット数が二倍になるため、回路規模は三倍程度増加したものとなった。そのた め、消費電力も増加する。これは、従来手法のFA に相当する、冗長二進加算器 の回路規模がFA と比べて大きくなったことが原因である。このため、高速性を 維持しながら回路規模の縮小、消費電力の低減をはかることが今後の課題であ る。

謝辞

本研究を行うに際し、懇切丁寧な御指導を御鞭撻賜りました高知工科大学大 学院工学研究科基盤工学専攻電子・光システム工学コース矢野政顕教授に心か ら感謝いたします。また、同研究室の原央教授、橘昌良助教授、ほか矢野研究 室の皆様に心から感謝し、お礼申し上げます。

参考文献

路”，培風館，pp.155‐171， Octover1996. [3] 有山一弘，“冗長 2 進表現を用いた剰余数システムに関する研究”， http://www-tysm.ee.kanagawa-u.ac.jp/~toyo/data/master/1996Ariyama.pdf， pp.14‐25，1996. [4] 松村暢也，矢野政顕，“RSA 暗号に使用されている乗算剰余演算器の高速化”， 電気関係学会四国支部連合大会，p.189，2003. [1] 梶原裕輝，永田真，瀧和男，“RSA 用高速べき乗剰余演算器の設計”， 信学技報，Vol.102，No.476，pp.157‐162，November 2002. [2] 榎本忠儀，“入門から実用まで CMOS 集積回

付録

6 ビット×6 ビットの各乗算器の VHDL ソースコードを付録として示す。な

．Wallace tree, CLA を用いた 6 ビット乗算器の VHDL ソースコード

se IEEE.std_logic_1164.all; us

ntity multiplier66_FA is

port (X : in std_logic_vector(5 downto 0); Y : in std_logic_vector(

zero : in std_logic;

Z : out std_logic_vector(11 downto 0));

end multiplier66_FA; architecture rtl of multiplier66_FA is component FA port (A : in std_logic; B : in std_logic; C : in std_logic; S : out std_logic; C_out : out std_logic); end component;

component CLA_4

port (A : in std_logic_vector(3 downto 0); B : in std_logic_vector(3 downto 0); C : in std_logic;

S : out std_logic_vector(3 downto 0); C_out : out std_logic);

お、以下に示すVHDL ソースコードは最上位の階層のものである。 1 --- library IEEE; u use IEEE.std_logic_arith.all; e IEEE.std_logic_unsigned.all; e 5 downto 0);

end component; mponent HA

S : out std_logic;

4, X0Y5, X1Y0, X1Y1, X1Y2, X1Y3, X1Y4, X1Y5, X2Y0, 4, X2Y5, X3Y0, X3Y1, X3Y2, X3Y3, X3Y4, X3Y5, X4Y0, 4Y5, X5Y0, X5Y1, X5Y2, X5Y3, X5Y4, X5Y5, C00, C01, C02, C03, C04, C05, C06, C07, C08, C09, C10, C11, C12, C13, C14, C15, C16,

C21, C22, C23, C24, C25, S00, S01, S02, S03, S04, S05, S06, , S16, S17, S18, S19, S20, S21

: s

gnal A, B : std_logic_vector(7 downto 0);

egin

(0) <= X(0) and Y(0); nd Y(0);

Y(1); 2Y1 <= X(2) and Y(1); (1); co port (A : in std_logic; B : in std_logic; C : out std_logic); end component;

signal X0Y1, X0Y2, X0Y3, X0Y X2Y1, X2Y2, X2Y3, X2Y X4Y1, X4Y2, X4Y3, X4Y4, X C17, C18, C19, C20, S07, S08, S09, S10, S11, S12, S13, S14, S15 td_logic; si signal CC : std_logic; b Z X1Y0 <= X(1) a

X2Y0 <= X(2) and Y(0); X3Y0 <= X(3) and Y(0); X4Y0 <= X(4) and Y(0); X5Y0 <= X(5) and Y(0); X0Y1 <= X(0) and Y(1); X1Y1 <= X(1) and X

X3Y1 <= X(3) and Y X4Y1 <= X(4) and Y(1); X5Y1 <= X(5) and Y(1); X0Y2 <= X(0) and Y(2); X1Y2 <= X(1) and Y(2); X2Y2 <= X(2) and Y(2);

X3Y2 <= X(3) and Y(2); 4Y2 <= X(4) and Y(2); d Y(2);

Y(3); 5Y3 <= X(5) and Y(3);

; 3Y5 <= X(3) and Y(5); = X(4) and Y(5); 5Y5 <= X(5) and Y(5);

X0Y1, X1Y0, Z(1), C00); , X1Y1, X2Y0, S00, C01); , X2Y1, X3Y0, S01, C02); , X3Y1, X4Y0, S02, C03); , X4Y1, X5Y0, S03, C04); , X5Y1, zero, S04, C05); X0Y4, X1Y3, S05, C06); , X1Y4, X2Y3, S06, C07); , X2Y4, X3Y3, S07, C08); , X3Y4, X4Y3, S08, C09); , X4Y4, X5Y3, S09, C10); , X5Y4, zero, S10, C11); S00, C00, Z(2), C12); , S01, C01, S11, C13); X X5Y2 <= X(5) an

X0Y3 <= X(0) and Y(3); X1Y3 <= X(1) and Y(3); X2Y3 <= X(2) and Y(3); X3Y3 <= X(3) and Y(3); X4Y3 <= X(4) and X

X0Y4 <= X(0) and Y(4); X1Y4 <= X(1) and Y(4); X2Y4 <= X(2) and Y(4); X3Y4 <= X(3) and Y(4); X4Y4 <= X(4) and Y(4); X5Y4 <= X(5) and Y(4); X0Y5 <= X(0) and Y(5); X1Y5 <= X(1) and Y(5); X2Y5 <= X(2) and Y(5) X

X4Y5 < X

U00 : FA port map(zero, U01 : FA port map(X0Y2 U02 : FA port map(X1Y2 U03 : FA port map(X2Y2 U04 : FA port map(X3Y2 U05 : FA port map(X4Y2 U06 : FA port map(zero, U07 : FA port map(X0Y5 U08 : FA port map(X1Y5 U09 : FA port map(X2Y5 U10 : FA port map(X3Y5 U11 : FA port map(X4Y5 U12 : FA port map(zero, U13 : FA port map(X0Y3

U14 : FA port map(S05, S02, C02, S12, C14); S03, C03, S13, C15); S04, C04, S14, C16); X5Y2, C05, S15, C17); C06, zero, S16, C18); C07, C15, S17, C19); C08, C16, S18, C20); C09, C17, S19, C21); C10, zero, S20, C22); , C11, zero, S21, C23); 8&S17&S16&S12&S11; 19&C18&C14&C13&C12;

wnto 0), B(3 downto 0), zero, Z(6 downto 3), C24); wnto 4), B(7 downto 4), C24, Z(10 downto 7), C25); Z(11), CC); nd rtl; --- 6 ビット乗算器の --- to 0); wnto 0); U15 : FA port map(S06,

U16 : FA port map(S07, U17 : FA port map(S08, U18 : FA port map(S13, U19 : FA port map(S14, U20 : FA port map(S15, U21 : FA port map(S09, U22 : FA port map(S10, U23 : FA port map(X5Y5 A <= S21&S20&S19&S1 B <= C22&C21&C20&C U24 :

CLA_4 port map(A(3 do U25 :

CLA_4 port map(A(7 do U26 :

HA port map(C25, C23, e

---2．2 次 Booth, Wallace tree, BLCA を用いた

VHDL ソースコード ---library IEEE; use IEEE.STD_LOGIC_1164.ALL; use IEEE.STD_LOGIC_ARITH.ALL; use IEEE.STD_LOGIC_UNSIGNED.ALL; entity multiplier66_2 is

Port ( X : in std_logic_vector(7 down Y : in std_logic_vector(7 do

zero : in std_logic;

Z : out std_logic_vector(14 downto 0));

ownto 0); nto 0); Y_minus : in std_logic;

to 0); o 0); A2 : out std_logic_vector(5 downto 0);

A_bar_g0 : out std_logic; A_bar_g2 : out std_logic; C1 : out std_logic; nd component;

Port ( A0 : in std_logic_vector(5 downto 0); td_logic_vector(5 downto 0); ar1 : in std_logic; C2 : in std_logic; std_logic; ector(9 downto 0); end multiplier66_2;

architecture Behavioral of multiplier66_2 is component Booth_six is

Port ( X : in std_logic_vector(5 d X_minus : in std_logic;

Y : in std_logic_vector(5 dow A0 : out std_logic_vector(5 down A1 : out std_logic_vector(5 downt

A_bar_g1 : out std_logic; C0 : out std_logic; C2 : out std_logic); e component Wallace_tree_six is A1 : in std_logic_vector(5 downto 0); A2 : in s A_bar0 : in std_logic; A_b A_bar2 : in std_logic; C0 : in std_logic; C1 : in std_logic; one : in zero : in std_logic;

S : out std_logic_vector(10 downto 0); C_out : out std_logic_v

C_minus : out std_logic); omponent BLCA_six is ); B : in std_logic_vector(10 downto 0); : in std_logic; ic; ic; downto 0)); gnal A downto 0); _logic_vector(10 downto 0); ignal C_out : std_logic_vector(9 downto 0);

nto 0), zero, A0(5 downto 0), A1(5 downto 0), _bar_g1, A_bar_g2, C0, C1, C2);

map

0), A2(5 downto 0), A_bar_g0, A_bar_g1, A_bar_g2,

s;

, zero, zero, one, one, zero, one, end component;

c

Port ( A : in std_logic_vector(10 downto 0 g_minus1 q_minus1 : in std_logic; g_minus_bar1 : in std_log q_minus_bar1 : in std_logic; g_minus2 : in std_log q_minus2 : in std_logic; g_minus_bar2 : in std_logic; q_minus_bar2 : in std_logic; C_minus : in std_logic; S : out std_logic_vector(10 end component; si 0, A1, A2 : std_logic_vector(5

signal A_bar_g0, A_bar_g1, A_bar_g2, C0, C1, C2, C_minus : std_logic; signal S, CC : std

s begin

compBooth : Booth_six port map (X(5 downto 0), zero, Y(5 dow A2(5 downto 0), A_bar_g0, A compWallace : Wallace_tree_six port (A0(5 downto 0), A1(5 downto

C0, C1, C2, one, zero, S(10 downto 0), C_out(9 downto 0), C_minus); CC <= C_out(9 downto 0) & C_minu

compBLCA : BLCA_six port map

Z(10 downto 0)); end Behavioral; --- のVHDL ソースコード --- o 0); (11 downto 0); std_logic_vector(23 downto 0)); nd multiplier66_RB;

Port ( A : in std_logic_vector(1 downto 0); B : in std_logic_vector(1 downto 0); A_minus : in std_logic;

o 0));

ignal X0Y1, X0Y2, X0Y3, X0Y4, X0Y5, X1Y0, X1Y1, X1Y2, X1Y3, X1Y4, X1Y5, X2Y0, , X3Y0, X3Y1, X3Y2, X3Y3, X3Y4, X3Y5, X4Y0, X4Y1, X4Y2, X4Y3, X4Y4, X4Y5, X5Y0, X5Y1, X5Y2, X5Y3, X5Y4, X5Y5, C00,

6, C07, C08, C09, C10, C11, C12, C13, C14, C15, C16, ---3．冗長二進加算器を用いた 6 ビット乗算器 ---library IEEE; use IEEE.STD_LOGIC_1164.ALL; use IEEE.STD_LOGIC_ARITH.ALL; use IEEE.STD_LOGIC_UNSIGNED.ALL; entity multiplier66_RB is

Port ( X : in std_logic_vector(11 downt

Y : in std_logic_vector zero : in std_logic; Z : out e architecture rtl of multiplier66_RB is component RBcell B_minus : in std_logic;

C_minus : in std_logic_vector(1 downto 0); S : out std_logic_vector(1 downto 0); C : out std_logic_vector(1 downt end component;

s

X2Y1, X2Y2, X2Y3, X2Y4, X2Y5 C01, C02, C03, C04, C05, C0

C32, C33, S00, S01, S02, S03, S04, S05, S06, S07, S08, S09, S10, S11, S12, S13, S14, S15, S16, S17, S18, S19, S20, S21, S22, zz : std_logic_vector(1 downto 0);

3) nand Y(1)) nand (X(2) nand Y(0)); d (X(2) nand Y(1)); (X(4) nand Y(0)); nand Y(1)); 3Y0(0) <= (X(7) nand Y(1)) nand (X(6) nand Y(0)); 0)) nand (X(6) nand Y(1)); nd Y(0)); nand (X(10) nand Y(0));

Y(1)); d Y(3)) nand (X(0) nand Y(2)); 0Y1(1) <= (X(1) nand Y(2)) nand (X(0) nand Y(3)); (X(2) nand Y(2)); 1Y1(1) <= (X(3) nand Y(2)) nand (X(2) nand Y(3)); nand Y(3)) nand (X(4) nand Y(2)); and Y(3)); nd Y(2)); nd (X(6) nand Y(3)); nd (X(8) nand Y(2)); )); d Y(2)); Y(3)); nand Y(5)) nand (X(0) nand Y(4)); 0Y2(1) <= (X(1) nand Y(4)) nand (X(0) nand Y(5)); begin

Z(0) <= (X(1) nand Y(1)) nand (X(0) nand Y(0)); Z(1) <= (X(1) nand Y(0)) nand (X(0) nand Y(1)); X1Y0(0) <= (X(

X1Y0(1) <= (X(3) nand Y(0)) nan X2Y0(0) <= (X(5) nand Y(1)) nand X2Y0(1) <= (X(5) nand Y(0)) nand (X(4) X

X3Y0(1) <= (X(7) nand Y(

X4Y0(0) <= (X(9) nand Y(1)) nand (X(8) na

X4Y0(1) <= (X(9) nand Y(0)) nand (X(8) nand Y(1)); X5Y0(0) <= (X(11) nand Y(1))

X5Y0(1) <= (X(11) nand Y(0)) nand (X(10) nand X0Y1(0) <= (X(1) nan

X

X1Y1(0) <= (X(3) nand Y(3)) nand X

X2Y1(0) <= (X(5)

X2Y1(1) <= (X(5) nand Y(2)) nand (X(4) n X3Y1(0) <= (X(7) nand Y(3)) nand (X(6) na X3Y1(1) <= (X(7) nand Y(2)) na

X4Y1(0) <= (X(9) nand Y(3)) na

X4Y1(1) <= (X(9) nand Y(2)) nand (X(8) nand Y(3 X5Y1(0) <= (X(11) nand Y(3)) nand (X(10) nan X5Y1(1) <= (X(11) nand Y(2)) nand (X(10) nand X0Y2(0) <= (X(1)

X

X1Y2(0) <= (X(3) nand Y(5)) nand (X(2) nand Y(4)); X1Y2(1) <= (X(3) nand Y(4)) nand (X(2) nand Y(5)); X2Y2(0) <= (X(5) nand Y(5)) nand (X(4) nand Y(4)); X2Y2(1) <= (X(5) nand Y(4)) nand (X(4) nand Y(5)); X3Y2(0) <= (X(7) nand Y(5)) nand (X(6) nand Y(4));

X3Y2(1) <= (X(7) nand Y(4)) nand (X(6) nand Y(5)); X4Y2(0) <= (X(9) nand Y(5)) nand (X(8) nand Y(4)); X4Y2(1) <= (X(9) nand Y(4)) nand (X(8) nand Y(5)); ) <= (X(11) nand Y(5)) nand (X(10) nand Y(4)); 5Y2(1) <= (X(11) nand Y(4)) nand (X(10) nand Y(5)); X5Y2(0

X

X0Y3(0) <= (X(1) nand Y(7)) nand (X(0) nand Y(6)); X0Y3(1) <= (X(1) nand Y(6)) nand (X(0) nand Y(7)); X1Y3(0) <= (X(3) nand Y(7)) nand (X(2) nand Y(6)); X1Y3(1) <= (X(3) nand Y(6)) nand (X(2) nand Y(7)); X2Y3(0) <= (X(5) nand Y(7)) nand (X(4) nand Y(6)); X2Y3(1) <= (X(5) nand Y(6)) nand (X(4) nand Y(7)); X3Y3(0) <= (X(7) nand Y(7)) nand (X(6) nand Y(6)); X3Y3(1) <= (X(7) nand Y(6)) nand (X(6) nand Y(7)); X4Y3(0) <= (X(9) nand Y(7)) nand (X(8) nand Y(6)); X4Y3(1) <= (X(9) nand Y(6)) nand (X(8) nand Y(7)); X5Y3(0) <= (X(11) nand Y(7)) nand (X(10) nand Y(6)); X5Y3(1) <= (X(11) nand Y(6)) nand (X(10) nand Y(7)); X0Y4(0) <= (X(1) nand Y(9)) nand (X(0) nand Y(8)); X0Y4(1) <= (X(1) nand Y(8)) nand (X(0) nand Y(9)); X1Y4(0) <= (X(3) nand Y(9)) nand (X(2) nand Y(8)); X1Y4(1) <= (X(3) nand Y(8)) nand (X(2) nand Y(9)); X2Y4(0) <= (X(5) nand Y(9)) nand (X(4) nand Y(8)); X2Y4(1) <= (X(5) nand Y(8)) nand (X(4) nand Y(9)); X3Y4(0) <= (X(7) nand Y(9)) nand (X(6) nand Y(8)); X3Y4(1) <= (X(7) nand Y(8)) nand (X(6) nand Y(9)); X4Y4(0) <= (X(9) nand Y(9)) nand (X(8) nand Y(8)); X4Y4(1) <= (X(9) nand Y(8)) nand (X(8) nand Y(9)); X5Y4(0) <= (X(11) nand Y(9)) nand (X(10) nand Y(8)); X5Y4(1) <= (X(11) nand Y(8)) nand (X(10) nand Y(9)); X0Y5(0) <= (X(1) nand Y(11)) nand (X(0) nand Y(10)); X0Y5(1) <= (X(1) nand Y(10)) nand (X(0) nand Y(11)); X1Y5(0) <= (X(3) nand Y(11)) nand (X(2) nand Y(10)); X1Y5(1) <= (X(3) nand Y(10)) nand (X(2) nand Y(11)); X2Y5(0) <= (X(5) nand Y(11)) nand (X(4) nand Y(10)); X2Y5(1) <= (X(5) nand Y(10)) nand (X(4) nand Y(11)); X3Y5(0) <= (X(7) nand Y(11)) nand (X(6) nand Y(10));

X3Y5(1) <= (X(7) nand Y(10)) nand (X(6) nand Y(11)); X4Y5(0) <= (X(9) nand Y(11)) nand (X(8) nand Y(10)); X4Y5(1) <= (X(9) nand Y(10)) nand (X(8) nand Y(11)); X5Y5(0) <= (X(11) nand Y(11)) nand (X(10) nand Y(10));

ownto 2), C00); C00, S00, C01); C01, S01, C02); C02, S02, C03); C03, S03, C04); , S04, C05); C06); , C06, S06, C07); , C07, S07, C08); C08, S08, C09); C09, S09, C10); , S10, C11); wnto 4), C12); Z(7 downto 6), C13); 11, C14); 12, C15); 13, C16); 14, C17); , C18); , C19); , C20); 20, S18, C21); 21, S19, C22); 22, S20, C23); 23, S21, C24); S22, C25); nto 8), C26); (11 downto 10), C27); X5Y5(1) <= (X(11) nand Y(10)) nand (X(10) nand Y(11));

zz <= zero & zero;

comp00 : RBcell port map(X0Y1, X1Y0, zero, zero, zz, Z(3 d comp01 : RBcell port map(X1Y1, X2Y0, X0Y1(1), X1Y0(1), comp02 : RBcell port map(X2Y1, X3Y0, X1Y1(1), X2Y0(1), comp03 : RBcell port map(X3Y1, X4Y0, X2Y1(1), X3Y0(1), comp04 : RBcell port map(X4Y1, X5Y0, X3Y1(1), X4Y0(1), comp05 : RBcell port map(X5Y1, zz, X4Y1(1), X5Y0(1), C04 comp06 : RBcell port map(X0Y3, X1Y2, zero, zero, zz, S05, comp07 : RBcell port map(X1Y3, X2Y2, X0Y3(1), X1Y2(1) comp08 : RBcell port map(X2Y3, X3Y2, X1Y3(1), X2Y2(1) comp09 : RBcell port map(X3Y3, X4Y2, X2Y3(1), X3Y2(1), comp10 : RBcell port map(X4Y3, X5Y2, X3Y3(1), X4Y2(1), comp11 : RBcell port map(X5Y3, zz, X4Y3(1), X5Y2(1), C10 comp12 : RBcell port map(S00, X0Y2, zero, zero, zz, Z(5 do comp13 : RBcell port map(S01, S05, S00(1), X0Y2(1), C12, comp14 : RBcell port map(S02, S06, S01(1), S05(1), C13, S comp15 : RBcell port map(S03, S07, S02(1), S06(1), C14, S comp16 : RBcell port map(S04, S08, S03(1), S07(1), C15, S comp17 : RBcell port map(C05, S09, S04(1), S08(1), C16, S comp18 : RBcell port map(zz, S10, C05(1), S09(1), C17, S15 comp19 : RBcell port map(zz, C11, zero, S10(1), C18, S16 comp20 : RBcell port map(X0Y5, X1Y4, zero, zero, zz, S17 comp21 : RBcell port map(X1Y5, X2Y4, X0Y5(1), X1Y4(1), C comp22 : RBcell port map(X2Y5, X3Y4, X1Y5(1), X2Y4(1), C comp23 : RBcell port map(X3Y5, X4Y4, X2Y5(1), X3Y4(1), C comp24 : RBcell port map(X4Y5, X5Y4, X3Y5(1), X4Y4(1), C comp25 : RBcell port map(X5Y5, zz, X4Y5(1), X5Y4(1), C24, comp26 : RBcell port map(S11, X0Y4, zero, zero, zz, Z(9 dow comp27 : RBcell port map(S12, S17, S11(1), X0Y4(1), C26, Z

comp28 : RBcell port map(S13, S18, S12(1), S17(1), C27, Z(13 downto 12), C28); 5 downto 14), C29); 7 downto 16), C30); (19 downto 18), C31); (21 downto 20), C32); omp33 : RBcell port map(zz, C25, C19(1), S22(1), C32, Z(23 downto 22), C33); nd rtl;

---

comp29 : RBcell port map(S14, S19, S13(1), S18(1), C28, Z(1 comp30 : RBcell port map(S15, S20, S14(1), S19(1), C29, Z(1 comp31 : RBcell port map(S16, S21, S15(1), S20(1), C30, Z comp32 : RBcell port map(C19, S22, S16(1), S21(1), C31, Z c

e