不等分散をもつ関数関係モデルの選択
Selection for functional relationship models with different variances
数学専攻 守屋 順之
全文
数学専攻 守屋 順之
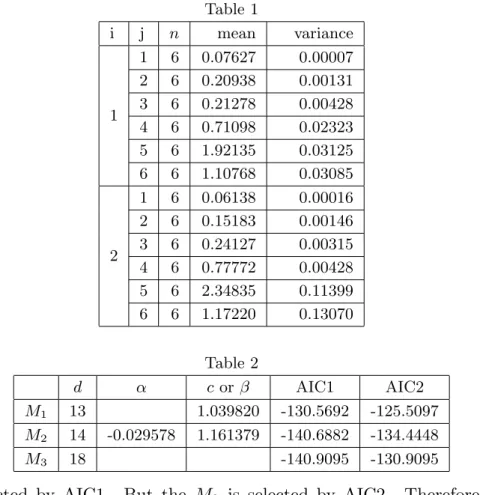
図
関連したドキュメント
The inclusion of the cell shedding mechanism leads to modification of the boundary conditions employed in the model of Ward and King (199910) and it will be
In this paper, we study the generalized Keldys- Fichera boundary value problem which is a kind of new boundary conditions for a class of higher-order equations with
On the other hand, from physical arguments, it is expected that asymptotically in time the concentration approach certain values of the minimizers of the function f appearing in
Kilbas; Conditions of the existence of a classical solution of a Cauchy type problem for the diffusion equation with the Riemann-Liouville partial derivative, Differential Equations,
Answering a question of de la Harpe and Bridson in the Kourovka Notebook, we build the explicit embeddings of the additive group of rational numbers Q in a finitely generated group
Then it follows immediately from a suitable version of “Hensel’s Lemma” [cf., e.g., the argument of [4], Lemma 2.1] that S may be obtained, as the notation suggests, as the m A
In our previous paper [Ban1], we explicitly calculated the p-adic polylogarithm sheaf on the projective line minus three points, and calculated its specializa- tions to the d-th
Definition An embeddable tiled surface is a tiled surface which is actually achieved as the graph of singular leaves of some embedded orientable surface with closed braid