Three Dimensional Large Amplitude Shallow Water Wave (Mechanisms and Mathematical Aspects of Nonlinear Wave Phenomena)

ThreeDimensional LargeAmplitudeShallow Water Wave TomoakiHirakawa,MakotoOkamura

InterdisciplinaryGraduate School ofEngineeringScience EarthSystemScience Technology

KyushuUniversity

1.

Introduction

Fluidphenomena aroundusoften cannot beseen.Waterwaves arephenomenathat commonlyand clearlyseen inourordinarylife. And suchwaterwavemotion isanattractivesubjectoffluiddynamics.Thoroughumde1standing ofthe phenomenonisnotsimple andmanyworkshave beendoneonwaterwave.

Above all, three-dimensional interactions of solitary

waves

have been actively studied for the last several decades. Although KoIteweg-de Vries $(KdV)$equation has been known for solitary waves, intemtions ofsolitary

waves

attracted muchattention afteraproposition ofMiles’ theo1y(1981)andaderivation ofapproximatedequations

such as the Kadomtsev-Petviashvili (KP) equation(1970). Anexperiment of thereflection ofsolitarywavesthat coresponds to theinteractionof

an

incident

wave

andits reflected wave

was

firstconducted by Perroud(1956).$A$

vertlcalreflecting wall

was

obliquelysetinawatertank,sothat

an

incident

wave

traingenerated along the tankcanhit the reflectingwallatanangle andinteract withitsownreflectedwave. Hefoumdoutthatwhenanincidentwave rmpingesonthereflectingwall,the incidentand the 1eflectedwavesstronglyinteracteachother and thewaveform of theinteracnng region resembles Mach reflection thatwasknownasaphenomenon of compressibleshockwaves. Although the accuracy of the experiment

was

not high because ofa deficient wave generator, measurement insmnents and the small watertank, the realizationofMach reflection in the interaction ofsolitary

waves was

remarkable. After20 years ofthe finding, Miles(1977)theoreticallyinvestigatedreflectionsof solitary

waves

inthe caseofsmallamphtude shallow waterwaves $\epsilon<<1(\epsilon=a_{i}/d$ : $\epsilon=the$nonlinear_parameter,

$a_{i}=$ theincident

waveamplitude, $d=$ _{the uniform waterdepth).} Heobtainedthesolution forthe oblique inte1action betweentwo solitons and provided an asymptotic description ofthe diffiactionofa soliton at the $\infty mer$ ofinteraction angle $-\sqrt{3\epsilon}<\psi<\sqrt{3\epsilon}$_.Hepredicted that themaximum mnup_{ofan incident wavebecomesfourtimeshigher than the}

incidentwave amplitude. Tanaka’s numerical 1esultfor $\epsilon=0.3$ shows better_{agreement withthe prediction for}

non-g1azing reflection than theprediction for strong resonantinteraction. Stationarystateswerealsonotattainedwhen it

was

closeto $\psi=\sqrt{3\epsilon}$_.Recently, Yeh,Li&Kodama₍₂₀₁₀₎havemodified theinteraction_pa1ameter

usedinMiles’ theory. This modification affects

some

$res\Lambda ts$ when the intemtion angle becomes relatively large. Using a new

modified interactionparameter, the $Ies\iota Ut$proposed byTanaka agrees with that ofMiles’ _{$ffi\infty Iy$}for non-g1azing

reflection better than that of theresonantinteractionmodel. Li,Yeh&Kodama(2011)conducted experimentsfor reflection ofan obliquely incident solitary wave at a veltical wall in the laboratory wave tank in the

cases

of $\in=0.076-0.367$ with $\psi=30^{o}$ and $20^{o}$. This laboratory experiment presents results suppoting Miles’

theoretical predictions,aswellasgood agreementwithTanaka’s numerical result

Inthisstudy,weextendweakly nonlinearinteractionsofshallowwaterwavesto strongnonlinear

cases

witha numericalscheme,suchasthe Newtonmethodand theGaleIkmmethod,and calculateperiodicsteadystatesolutions. Awavebecomesasolitarywaveinshallow water thatisnotperiodic.Becausesucha nonperiodicwave isdifficultto beformed withperiodic functions,wedecideparameters

so

thata waveforms flat surface between adjacentwave crests. When the nonlinear parameter $\epsilon$ issmall,mostofour results well reproduce Miles’theo1y.However,inrather

strong nonlinearity

cases

of$\epsilon>0.1$_,

our

oesMts do _not agreewell with Miles’ theo1y because the nonlinearity

parameter $\epsilon$ in this studyisoutofMiles’approximation ofweakdy nonlinearity $\epsilon$ く$<$ $1.$This tendencyisnatural and

already$repoIt\propto 1$by otherresearchers.

2.

Formulation of the problem

2.1

Fundamentalequationforwater

waves

We consider fiee surface gravity

waves

on an inviscid, incompressible fluid of uniform depth and also

$i_{IT}$otationdflowis assuned. $d$ is anuniform depth, $\phi$ is velocitypotential, $z=\eta(x,y, t)$ issurface displacement, $\chi,$$y$ arehonzontal coordinates and $z$ isve1tical coordinate. Fumdamental equations forwaterwaves arewrittenas

follows

$\phi_{t}+\frac{1}{2}\nabla\phi\cdot\nabla\phi+gz=0$

on $z=\eta(x, y, t)$ (22)

$\frac{D}{Dt}(\frac{P}{\rho})=(\frac{\partial}{\partial r}+\nabla\phi\cdot\nabla)[\phi_{t}+\frac{1}{2}\nabla\phi\cdot\nabla\phi+gz]=0$ on _{$z=\eta(x,y, t)$}

(2.3)

$\phi_{Z}=0$ as $z=-d$ _(2.4)

where $g$ isthegravitationalacceleration. Equation(2.3)is aLagrangederivative ofBemoulli’s equation_(22).In

stead ofequation(2.3),equationof Lagrangederivativeofafimction$F(x,y,z, t)=z-\eta(x,y, t)=0$ onthe free surface $z=\eta(x,y, t)$ can_{be used for the boundary condition:}

$\frac{DF}{Dt}=(\frac{\partial}{\partial t}+\nabla\phi\cdot\nabla)F=0$

on

$z=\eta(x,y, t)$ (2.5)

However,thisequationincludesthe fiee surface displacement $\eta(x,y, t)$ as an

_unknow1L

_{forthis reason, wemust}

reduce$\eta by\propto|$uation($22)$._Inthispoint because equation_(2.3)isa$f_{0I}m$aheady

$\eta$ isreduced,(2.3)isuseful.

2.2

Formulation for$numeI^{\cdot}$ical calculation

Wenornalize vanablesasfollows.

$(x^{*},y^{*},z^{*}, H^{*})=(Kx, Ky, Kz, KH)$, $t^{*}=\omega t,$ $\Phi^{*}=\frac{K^{2}}{\omega}\phi,$ $G= \frac{K}{\omega^{2}}g$, (2.5)

where $K$ is awavenumber, $\omega$ is afrequency ofan incidentwaterwave.

Inordertocalculateasteadyprogressive wave,

we

considermovingcoordinate,

$T=px^{*}-t^{*}, Y=qy^{*}, Z=z^{*}$

, (2.6)

Here, $p=\sin\theta,$ $q=\cos\theta$. Whena wavenumbervectorofsolitarywave $(k_{\chi/}k_{y})$_,wehave lelations:

$k_{x}=K\sin\theta,$ $k_{y}=K\cos\theta$, tane $=k_{x}/k_{y},$

Interactions pattem for solitary waves in$T$ and $Y$-axis canbe treated as periodof$2\pi$. Use equation _(2.6) and

substitute

as

$\Phi(Y, Z, T)=\Phi^{*}(x^{*},y^{*},z^{*}, H^{*}) , H(Y, T)=H(x^{*},y^{*}, t^{*})$_,

Using derived nondimensionalvariables,wechange the form ofthefundamentalequation for waterwaves asfollows.

$p^{2}\Phi_{TT}+q^{2}\Phi_{YY}+\Phi_{ZZ}=0$ _{for $Z\leq H(Y, T)$, (2.7)}

$P(Y_{t}Z_{r}T)=- \Phi_{T}+\frac{1}{2}(p^{2}\Phi_{T}^{2}+q^{2}\Phi_{Y}^{2}+\Phi_{Z}^{2})+GZ=0$ (2.8) on $Z=H(Y, T)$, $Q(Y,Z, T)=\Phi_{TT}+p^{2}\Phi_{T}(-2\Phi_{TT}+p^{2}\Phi_{T}\Phi_{TT}+q^{2}\Phi_{Y}\Phi_{YT}+\Phi_{Z}\Phi_{ZT})$ $+q^{2}\Phi_{Y}(-2\Phi_{YT}+p^{2}\Phi_{T}\Phi_{YT}+q^{2}\Phi_{Y}\Phi_{YY}+\Phi_{Z}\Phi_{YZ})$ $+\Phi_{Z}(-2\Phi_{ZT}+p^{2}\Phi_{T}\Phi_{ZT}+q^{2}\Phi_{Y}\Phi_{YZ}+\Phi_{Z}\Phi_{ZZ}+G)=0$ on $Z$ (2.9) $=H(Y, T)$, $\Phi_{Z}=0$ on $Z=-d$, (2.10)

Weintroducethewavesteepness

$WS= \frac{1}{2}[H(0,0)-H(\pi, O)]$ _(2.11)

which_{is halfofthe difference between the peak}$H(0,0)$ _andthetrough $H(\pi, 0)$.

Assumingthevelocitypotential $\Phi$

as

periodic

$\Phi(Y,Z, T)=\sum_{k=0}^{N}\sum_{j=1}^{N}X(Z)\cos(kY)$sinCT)_{, (2.12)}

andwe have atruncatedseriesasfollows:

$\Phi(Y_{\fbox{Error::0x0000}}Z,T)=\sum_{k\not\subset 0}^{N}\sum_{j=1}^{N}A_{k_{j}’}[\cosh(\alpha_{kj}Z)+\sinh(a_{kj}Z)\tanh(a_{kj}d)]\cos(kY)\sin(jT)$_,

(2.13)

$\alpha_{kj}=\sqrt{p^{2}j^{2}+q^{2}k^{2}}.$

3.

Numerical scheme

At firs,wenumerically calculate the freesurfacedisplacement by applying Newton’s methodtothe dynanuc boundary$\infty$ndition(2.8).The recurrent

$H_{n+1}=H_{n}- \frac{dZ}{dP(Y,H_{n\prime}T)}P(Y, H_{n}, T)$_{, (3.1)}

Next

we useGalerkm’smethod toobtain theindependent relationsforunknowns$A_{kj}$:

$F_{lm}(A_{lm/}G)= \int_{0}^{\pi}dY\int_{0}^{\pi}dTQ(Y, H(\mathcal{A}_{lm}, G), T)\cos(lY)\sin(mT)=0$_{, (3.2)}

(3.2)can$k$conside1edas$M$-point Fourier transfonn.Because when _$l+m$ isodd,_(3.2)ist1ivial,_{the numberof}

independent 1elatlons(32)is $M(M+1)/2$.Anotherindependentrelationisexpressedas

$W(A_{kj}, G)=2WS-[H(0,0,\cdot \mathcal{A}_{kj}, G)-H(\pi, 0,\cdot \mathcal{A}_{kj}, G)]=0$_{, (33)}

whichisa different expression ofthewavesteepness(2.11).Finally,we canobtainasufficient numberofindependent relations andwe

can

solve the nonlinear equations(3.2)and(3.3).Here,the third orderapproximationforshort-crested

wave

calculatedby Hsu$et$. al. (1979)isused

as

the imtial solution ofiteration.We stoptheiterationifthe difference

between unknowns beforeandafter iterationis smaller than $10^{-10}$_{. The numberofexpansion terms ofa solution}

$N(N+1)/2$ isset

as

$N=30$.The samplingpointforfflerkin’s method(two-dimensional$Fo\iota mer$transform)is

setas $2^{}.$

4.

Result

We calculated numerical solutions for various incident amplitudes, depths $d$ and angles of

incidentwaves $\theta$

bychanging initialconditions suchas

wave

steepness $WS$_,

an

initialdepths and

angles of wavecomponents $\theta_{i}$.Notethatwavecomponentswithanangle of $\theta_{i}$ not alwaysforman

incident wavewith the

same

angle and we

can

evaluate the angle ofan incident

wave

only from resulting waveforms. Anincident waveamplitudeisalsoevaluated from aresultas;

$a_{i}=H (\begin{array}{ll}\pi \pi\overline{2}^{1}\overline{2} \end{array})-H(\frac{\pi}{2}\prime 0)$ , (4.1)

because ofthesymmetriccondition.Andwedefine the $a_{M}$

as

thecenteroftheinteracting regionofwave profleas;

$a_{M}=H(0,0)-H( \frac{\pi}{2},0)$, (42)

that is the same

as

the definition ofwave steepness. Therefore, we define the ratio $a$ ofthe 1naximum wave

amplitude toanincidentwaveamplitude as;

$\alpha=\frac{a_{M}}{a_{i}}=\frac{H(0,0)-H(\frac{\pi}{2}\prime 0)}{H(\frac{\pi}{2}J\frac{\pi}{2})-H(\frac{\pi}{2}\prime 0)}=\frac{WS}{H(\frac{\pi}{2}\prime\frac{\pi}{2})-H(\frac{\pi}{2}\prime 0)}$, (4.3)

4.1

Weakly nonlinear

cases

In this section, we discuss weakly nonlinear

interactions.

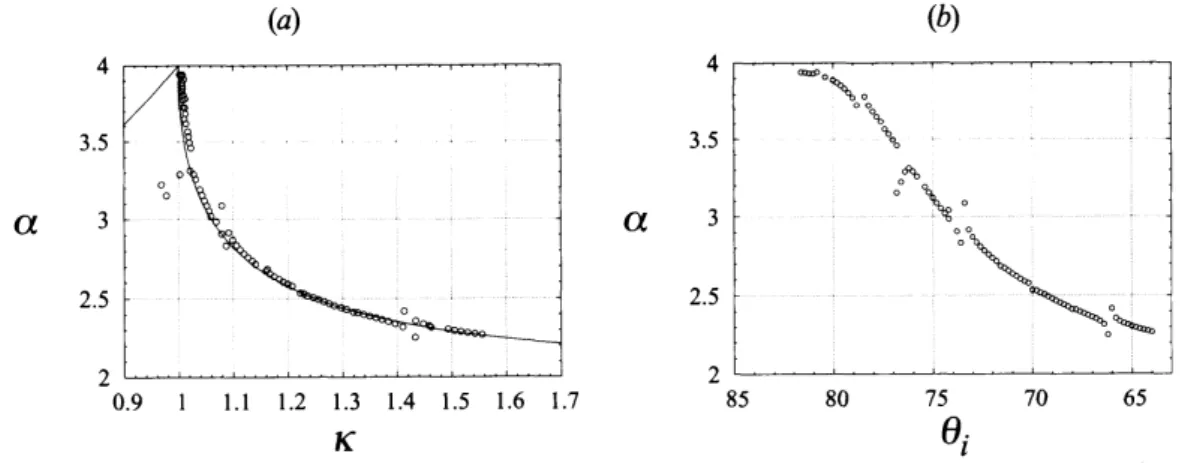
Asymptotic solutions of weakly nonlinear interactions are described by Miles’ theory. 4.1, 4.2 and 4.3 show comparisonsbetween Miles’ theory and numerical results in cases of $d=0.050,$ $d=0.070$ and $d=0.090$ and the

dependence of$\alpha$ respectto $\theta_{i}$. Because ofoursymmetric assumption ofasolution,a solution

can

not

be found for $\kappa<1.$

(a) (b)

$\alpha$

0.9 1 1.11.21.3141.51.61.7 85 80 75 70 65

$\kappa \theta_{i}$

Mostofourresults

are

well 1eproduced by Miles’ theory.However,somelarge and smalldiscrepanciesexisted. We will studyonthis

cause

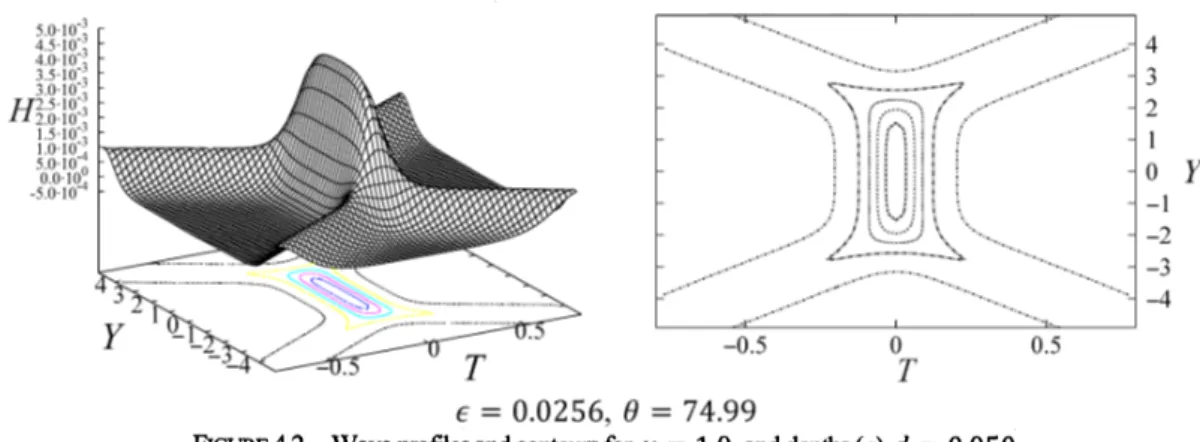
furthermo1eandcompareit withharmonicresonanceconditions Figure42showswave a profile andacontour for $\kappa=1.0$ _{and depths $d=0.050.$}

$4010_{3}^{\fbox{Error::0x0000}}4510_{2}5010_{3}^{-\urcorner}$ 4

.

$510_{\gamma}$ 3 $H_{2010_{3}^{3}}^{3010}2510^{-3}$ $-\fbox{Error::0x0000}$ 2 $\sim 50105010^{4}1010^{-3}15\cdot 100010_{4}^{0}$ $\angle_{\wedge}\prime\prime----ノ I\prime;\prime\fbox{Error::0x0000}\fbox{Error::0x0000}・\}\prime 蓚$ $–arrow\fbox{Error::0x0000}||s/\backslash \backslash \backslash$

$-2-101Y$

$-4-3$

$-0.5$ $0$ 0.5

$T$

$\epsilon=0.0256, \theta=74.99$

FIGURE4.2. Waveprofiles andcontoursfor $\kappa=1.0$ _{and depths(a) $d=0.050$}

When $\kappa=1.0$_,

interactions

of_{two solitary}waves are _{strongand aninteractionregion extendin} $Y$

direction. Aninteraction of two solitarywaves isthesame phenomena as reflectionofanincident solitarywave sothat Figure 4.2impliesastemextendsinperpendicular tothereflectingwall.

4.2

Harmonic

resonance

In many conditions, unexpected rough waves and bad convergence appear. They

seem

sporadic and unavoidableproblems.Mostofinteractingwaveprofilesthatdonotagree with that ofMiles’theory,

are

contaminatedby smallerwavecomponents. Those

contaminations occur

sporadically andmake it difficultforsolutionsto converge smoothly.

In order to investigated those deviations we sought regions enclosed with black frames (a) and

(b) in Figure 4.3 which is in the case of fixed water depth $d=0.050$ and $0.025<\epsilon<0.050.$

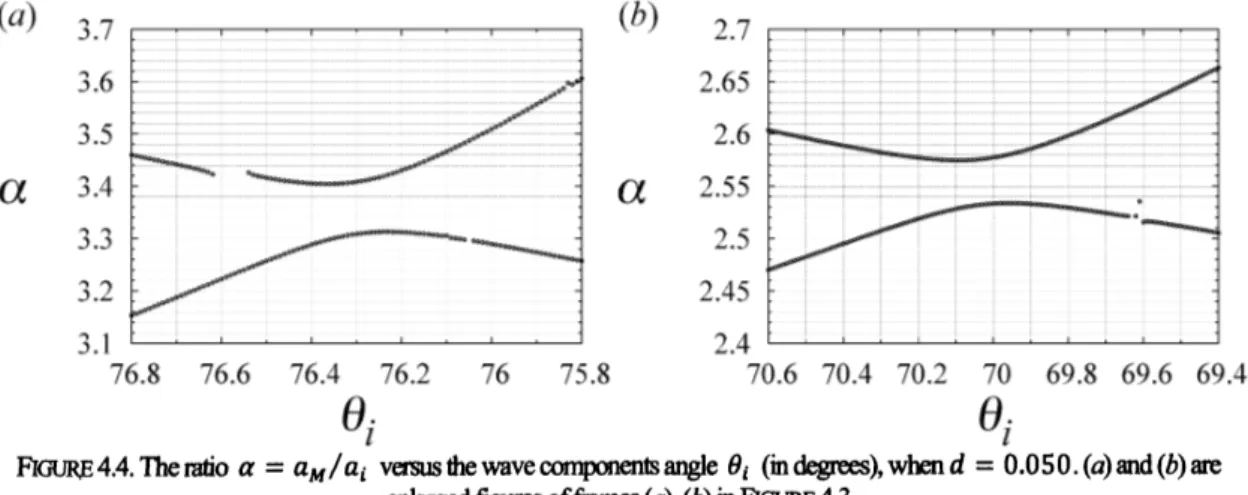
Figure4.4showsenlarged figuresofblackframes(o)and(b)inFigure4.3.

$\alpha$

$80 75 70 65$

$\theta_{i}$

(a)

$\alpha$

76.8 76.6 76.4 76.2 76 75.8 70.6 70.4 70.2 70 69.8 69.6 69.4

$\theta_{i} \theta_{i}$

FIGURF 44.Theratio $a=a_{M}/a_{i}$ versusthewavecomponentsangle$\theta_{i}$ (indegrees),when$d=0.050.(a)$and(b)are

enlarged figures offiames(a), (b)in FIGURE4.3

Figure 4.4showsweobtained solutionsin pairs inmostofwave$\infty$mponentsangles $\theta_{i}$.At

ffist

wechecked

(b-3)

$45\cdot 10_{-3}^{-3}40\cdot 10_{3}35\cdot 10_{\sim 3}^{\vee^{\wedge}}$

30

$2510_{3\fbox{Error::0x0000}}$

$H_{1510_{3}^{-3}}^{20\cdot 10}$

10

$-50.10_{-3}・50.\cdot 10001Q_{4}^{0}$

FlGuRE4.5. The waveprofile of$(a);d=0.050,$$\theta_{i}=76.8,(b);d=0.05,$ $\theta_{i}=75.8,$

$(c);d=0.09, \theta_{i}=71.6,(d);d=0.09, \theta_{i}=70.8.$

Inthenextplace,wecheck absolute values ofdifferences betweeneachmodes $|\delta A_{kj_{i}\theta_{i}}|$ ofthosepairs;$(a-1)-$ (a-2),$(a-3)-(aA),$ $(b-1)-(b-2)$_and$(b-3)-(bA)$in Figure 4.5. $\delta A_{kj,\theta_{i}}$ isdefinedas;

$\theta_{i}=70.60^{o}$ $|\delta A_{kj,\theta_{i}}|$ $2010^{4}31560|0^{4}478.00(000|1||1|0^{4}0^{4}0^{4}0^{-4}0^{4}0^{4}|_{f}-$ $c_{5arrow}$ $j$ TO $arrow c/_{0}’$

FIGURE46.The absoluevalueofa diffenencecoefficient $|A_{kj,\theta_{i}}|$ fiom $(k,j)=(0,1)$to $(k,j)=(12,13)$

(i)

$\theta_{j}=75.90^{o}$

(ii)

$\theta_{i}=76.20^{o}$

(iii)

$\theta_{i}=76.50^{o}$

(iv)

$\theta_{i}=76.79^{o}$

FIGURE4.7.Theabsolute value ofadffienenoe coefficient $|A_{kj,\theta_{t}}|$ from $(k,j)=(0_{z}1)$ to $(k_{\Delta}j)=$ $(12,13)$:

(i)

$\theta_{i}=69.40^{o}$

(ii)

$\theta_{i}=69.80^{o}$

(iii)

$\theta_{i}=70.20^{o}$

(iv)

$\theta_{i}=70.59^{o}$

FIGURE4.8. The absolute value ofa diffenence coefficient $|A_{kj,\theta_{i}}|$ fiom $(k,j)=(0,1)$to $(k,j)=$ _$(12,13)$:

(1) $\theta_{i}=69.40^{o}$, (ii)$\theta_{i}=69.80^{o}$,(iii) $\theta_{i}=70.20^{o}$, (iv) $\theta_{i}=70.59^{O}.$

(a) (b)

76.8 76.6 76.4 76.2 76 75.8 70.6 70.4 70.2 70 69.8 69.6 69.4

$\theta_{j} \theta_{i}$

FIGURE4.9.The value ofadiffenence coefficient $A_{kj,\theta_{i}}.$$(a)$,(b)coresspondtoenlargedfigure of frames(a),(b)

in FIGURE4.3.

We make it clear weather those rough waves instabihties

are

occurred by an effect of a harmonic

resonance

or not. The harmonic

resonance

ofthreedimensional interactions of water waves for finite depth and weakly nonlinearity

cases

is known to exist (Ioualalen 1996) _if

interactions

ofwavessatisfy

$a_{kj}\tanh(\alpha_{kj}d)=j^{2}tanh(d)$ _(4.6)

where solutions form

are

written as

$\Phi(Y,Z,T)=\sum_{k=0}^{N}\sum_{j=1}^{N}A_{kj}[\cosh(a_{kj}Z)+\sinh(\alpha_{kj}Z)\tanh(\alpha_{kj}d)]\cos(kY)\sin 0T)$_, $\alpha_{kj}=\sqrt{p^{Z}j^{2}+q^{2}k^{2}}$

Because equation (4.6) _is only dependent on $d,$ $k,$$j$ and $\theta$, when water depth $d$ is given, we can

makea tablethatshows harmonic

resonance

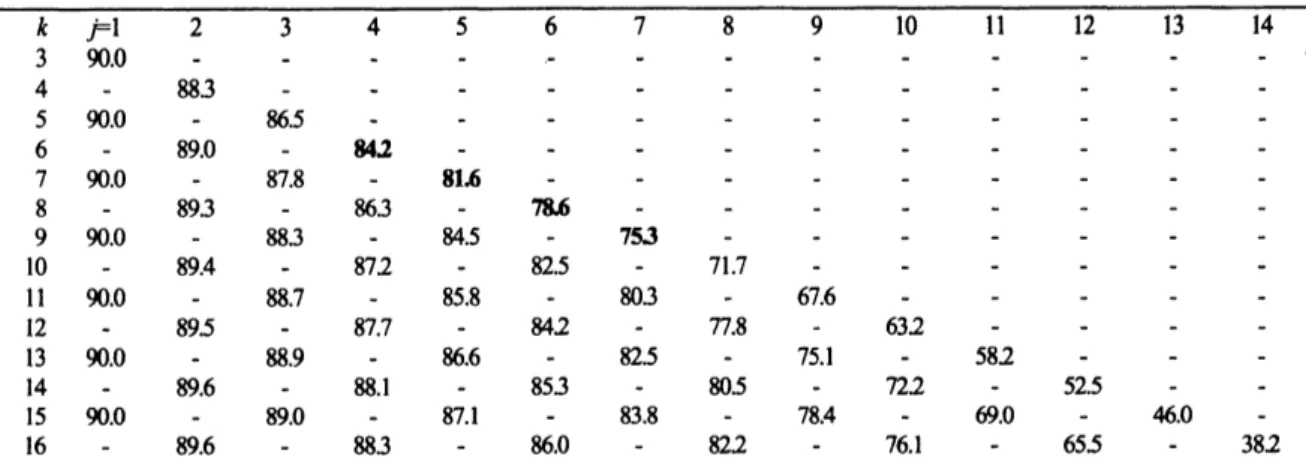
angle $\theta_{HR}$.TABLE4.1showsharmonic

resonance

angles $\theta_{HR}$ when $d=0.050$

$k$ $\Gamma^{-1}$ 2 3 4 5 6 7 8 9 IO 11 12 13 14 3 $\Re).0$ 4 883 5 $\mathfrak{A})0-$ 86.5 6 $-$ 890 84.2 7 900 87.8 $81^{-}.6$ 8893 863 $-$ 7&6 9 90.0 883 84.5 $75J$ IO 894 872 82.5 717 II $\mathfrak{A}J.0$ 88.$7$ 858 80.$3$ 676 I2 895 87.7 842 77.8 $63^{-}2$ 13 $(X).0$ 889 86.$6$ 82.$5$ 75.$1$ 582 I4 - 89.6 88.$1$ 853 80.$5$ 722 $52^{-}.5$ 15 $\Re]0$ 890 87.$1$ 838 784 69.$0$ 46.$0$ $-$ $16$ $89^{-}.6$ 88.$3$ $-$ 86.$0$ 822 76.$1$ $-$ 655 382

TABLE4.1.Harmomcresonanceangles $\theta_{HR}$ (indegrees)when$d=0.050$.Harmonicresonanceangles $\theta_{HR}$

when $(k,j)=(6,4)$,$(7_{\fbox{Error::0x0000}}5)$,$(8,6)$ and $(9,7)$ arewritten_$m$bold

We couldn’t find good agreement between hamlonic resonance angles $\theta_{HR}$ and the angle where those

discrepancies occur. Harmonicresonanceangles $\theta_{HR}$ when $(k,j)=(6,4)$,$(7,5)$,$(8,6)$ and$(9,7)$ are84.2, 81.6,78.6

and753.Accordingly, angles of frames(a)and(b)inFigure4.3werenoagreement wth hannonicresonanceangles.Because

harmonicresonanceanglesarebasedonlinear theory,$nonlineaI\rceil ty$might have effectedonthose angles.

4.3

Strong nonlinear

cases

In this section, we discuss rather strong nonlinearinteractions. In thecase ofrather large $\epsilon,$

results

are

unstable and solutions become more difficult to converge thanweakly nonlinearcases. Bad convergences sporadically occur with changing conditions and often result in rough wave interactionprol][les.Followingfigures shownumerical resultscorresponding to $\epsilon=0.2$_,0.3.

(X

$\kappa$

FIGURE4.10.Thetatio $a=a_{M}/a_{i}$ versustheinteraction parameter $\kappa$ when$\epsilon=0.20.$

$\alpha$

$\kappa$

In the

case

of rather large $\epsilon$, numerical results do not agree with Miles’ theory because

nonlinearityparameter $\epsilon$ isoutofMiles’approximation of weakly nonlinearity $\epsilon<<1.$

Figure 4.10 and 4.11 differs depending on water depths $d$. However, even if the depth $d$ is

different,results should show thesameresult when $\epsilon$ arethesamebecause theratio $d/2\pi$ ofthe

depth $d$ tothe wavelength $2\pi$,which associatedwithsolitaryofwaves,isset sufficientlysmallto be

assumed the wavelength

as

infinity for

waves in

an

cases,such

a

smallchange

in

depths $d$ should

notaffect to thesolutions.

For

various

conditions excluding the critical

cases

around $\kappa=1$ and Mach reflection region

$\kappa>1$_, there

are cases

thatresults shows rough waves or become unstable and do not converge

enoughwhichpreventedustoobtainfavorabledata in succession. Those deviations arelarger than those

occur

inweaklynonlinear

cases.

$H$ $-15$ $-1$ $-05$ $0T$ 05 1 15 (o) 012 01 $0$os 006 $H$ 0.04 002 $0$ 002 $-15 -1 -05 0_{T}05 I 15$ (b)

FIGURE4.12. Wave profilesandcontou1sfor$\kappa=1.0$ _{and depths(a)}$\epsilon=0.2$ and_(b) $\epsilon=0.3.$

5. Conclusion

The scheme used in this 1esearch

was

successful to obtain solutions forthree limensional large amplitude shallowwaterwaveof$\epsilon$ upto0.5.When $\in$ issmall,mostofournumericalresults show good agreement withMiles’

theory.However,

some

discrepanciesexistand we observed

wave

profilesbecame rough anddifficultto convergence in those cases. They occur sporadically and we couldn’t avoid such rough waves of solutions by reducingstepsin calculations ofthe Newton method. Andas$\epsilon$ increases, starts decreasing

and differencesbetween thenumerical results and Miles’ theory increaseand resulting waveprofiles tend to be contaminatedwhen $\kappa$ is closeto1.

Existence of hannonic

resonances

has been knownforperiodic solutions ofweakdy nonlinear shallowwater

waves.

Because thesolutionsusedinthis study

are

periodic, the solutions

aso

havepossibility toshowharmonic

resonances.

Angles of fiames(a)and(b)inFiguIe4.3werenoagreement with hartnonicresonanceangles. Becauseharmonic

Reference

[1]

_Ablowitz

MJ.

&Baldwin,

DE.,2012.Nonhnear shffiow

ocean

wavesolitoninteractions

on

flat beaches.

[2] Concus, P., 1962. Standing capillary gravitywavesoffiniteamplitude.Journal

_ofFluid

Mechanics,

pp.568-576.

[3] Fultz,D., 1962.Anexperimental noteonfinite-amphtudestandinggravity

waves.

Joumal

_offluid

mechanics.

Funakoshi, M.,1980.ReflectionofObliquely Incident SolitaryWaves.pdf

[4] Hammack, J.,_{1989. Two-dimensional periodic}

_waves

_{in shallowwater.Joumal ofFluidMechmics, Hammack,}

J.,1995.Two-dimensional periodic

waves

inshallow water. Part2. Asymmetric

waves.

JFluidMech,285.

[5] Hsu, J.,_{1979. Third-order}approximationtoshort-crested

waves.

Joumal

_{ofFluidMechanics}

[6] Ioualalen,M.&Kharif,C.,1993.Stabilityofth1eedimensional p1ogressive$\Psi^{vity}$

waves

ondeep

waoer

to

supe1harmonicdisturbances.Eur. J. Mech. B.FluidS,pp. 401-414.

[7] Ioualalen,M.,Roberts,

a

J.&Kharif,C., 1996.Onthe observabihty offinite-depth short-crestedwater

waves.

JournalofFluidMechanics, 322,pp. 1-19.

[8] Ioualalen, M. & Kharlf, C., 2006. On the subharmonic instabilities ofsteady three-dimensional deep water waves.Journal ofFluidMechanics,$262(-1)$,p.265.

[9] Kadomtsev,B.B.&Petviashvili,V.I.,1970. Onthestability ofsoliffiywavesin weakdy dispersive media. Sov.

Phys. Doklady, 15,pp.539-541.

[10] KnickerbockerNewel,1985.Reflectionsfiomsolitarywavesinchannels ofdec.

[11] Kodama, Y., Oikawa,M. &Tsuji,H.,2009. Soliton solutionsofthe KPequationwith$V$-shapeinitialwaves.

JournalofPhysics A:$Mathemat\iota cd$and

_Theoretical

_{42(31),p.312001.}

[12] Laitone, E.V, 1962.Limiting ConditionsforCnoidalandStokesWaves.JournalofGeophysicalResearch,67(4),

pp.1555-1564.

[13] Li,W.,Yeh, H.&

Kodama.

Y.,2011. Onthe Mach reflectionofasolitary

wave:

1evisited.Journal

_ofFluid

Mechanics, 672,pp.326-357.

[14] Miles, J.W.,1977. Noteon asolitarywave.Journal ofFluidMechanics,pp. 149-152.

[15] Miles, J.W.,1977aObliquelyinteracting solitarywaves.JournalofFluidMechanics,79.

[16] Miles, J.W.,1977b.OnHamilton’sprinciple forsurfhcewaves.Journal ofFluidMechanics,83(01),p. 153.

[17] Miles, J.W.,1977c.Resonantlyinteracting solitary

waves.

JoumalofFluidMechanics, 79,pp.171-179.

[18] Miles, J.W., 1981. The KortewegdeVries equation: a historical essay.Journal

_ofFluid

Mechanics, $106(-1),$

p.131.

[19] Okamum$*$M.,2010. Almostlimitingshort-crested gravitywavesindeepwater.Journal

ofFluid

Mechanics,

646,p.481.

[20] Tanaka, M., 1993. Mach reflection ofa large-amplitude solitary

wave.

Journal

_of

FluidMeckmcs, 248,

pp.637-661.

[21] Tanaka,M.,1986.Thestability ofsolitarywaves.Phys.Fluids.

[22] Tsai,C.-P.&Jeng,D.-S.,

1994.

Numerical Foumier solutions ofstanding

waves

in finitewaterdepth.

[23] _Wineberg,S.

_&McGrath

J., 1991. Implicitspectral methodsforwavepropagation problems.Journal

_ofFluid

Mechanws,336.

[24] Yeh, H.,Li, W.&Kodama,Y.,2010.Machreflectionand KPsolitonsin shallowwater.,p.16.

InterdisciplinaryGraduate SchoolofEngineering Science Kyushu

University

6-1 Kasuga-Koen, Kasuga

816-8580

Japan

E-mail address:

$t$

-hirakawa@riam.kyushu-u.ac.jp