Wulff shapes and their duals (Singularity theory of differential maps and its applications)

Wulff

_shapes

and their

duals

Huhe Han*

Graduate School of Environment and

Information

_Sciences,

Yokohama National

_University

Takashi

Nishimurat

Research Institute of Environment and Information

_Sciences,

Yokohama National

_University,

1

Introduction

The Wulff construction is well‐knownas a_geometricmodel ofanequilibrium

crystal

definedas follows.

Letn be a_positive

_integer.

Given acontinuous function _$\gamma$ : S^{n} \rightarrow

_\mathbb{R}+

where S^{n} \subset\mathbb{R}^{n+1} isthe unit

sphere

and

_{\mathbb{R}_{+}}

istheset_consistingof_positiverealnumbers, the Wulff shapeassociated with $\gamma$,denoted

by

\mathcal{W}_{ $\gamma$}

,isthe

following

intersection

(see

Figure

1)

\displaystyle \mathcal{W}_{ $\gamma$}=\bigcap_{ $\theta$\in S^{n}}$\Gamma$_{ $\gamma,\ \theta$}.

Here,

$\Gamma$_{ $\gamma,\ \theta$}

isthe

_{following half‐space:}

$\Gamma$_{ $\gamma,\ \theta$}=\{x\in \mathbb{R}^{n+1} |x\cdot $\theta$\leq $\gamma$( $\theta$)\}.

By

Wulffconstruction, weknow that Wulff_shape isa _compact, convex and contains the the_originof

Figure

1: AWulff

shape

\mathcal{W}_{ $\gamma$}.

\mathbb{R}^{n+1} as an interior_point.

Conversely,

it is well‐known that_anyconvex

_body

Wcontainsthe

origin

as

*

han‐huhe‐bx@ynu.jp $\dagger$_{nishimura‐takashi‐yx@ynu.jp}

aninterior_point isaWulff

shape

given

by

appropriate support

function, namely,

there isacontinuous

function $\gamma$:

S^{n}\rightarrow \mathbb{R}_{+}

such that

_{\mathcal{W}_{ $\gamma$}=W}

. For detailsonWulff

shapes,

seeforinstance

[1,

6, 13,

14].

Foracontinuousfunction _$\gamma$:

S^{n}\rightarrow \mathbb{R}+

,set

graph

( $\gamma$)=\{( $\theta$, $\gamma$( $\theta$))\in \mathbb{R}^{n+1}-\{0\}| $\theta$\in S^{n}\},

where

_{( $\theta$, $\gamma$( $\theta$))}

is the

_{polar plot}

expressionforapointof

\mathbb{R}^{n+1}-\{0\}

. The

mapping

inv:

\mathbb{R}^{n+1}-\{0\}\rightarrow

\mathbb{R}^{n+1}-\{0\}

,definedas

follows,

iscalled theinversionwithrespectto the

origin

of\mathbb{R}^{n+1}.

\displaystyle \mathrm{i}\mathrm{n}\mathrm{v}( $\theta$, r)= (- $\theta$, \frac{1}{r})

.

Let

_{\mathrm{P}_{ $\gamma$}}

be the

_boundary

of theconvexhull of

_{\mathrm{i}\mathrm{n}\mathrm{v}(\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}( $\gamma$))}

.

Definition 1

_{([12, 10])}

Let $\gamma$ : S^{n} \rightarrow

_\mathbb{R}+

be acontinuousfunction. If the

equality

$\Gamma$_{ $\gamma$}

=

\mathrm{i}\mathrm{n}\mathrm{v}(\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}( $\gamma$))

is

satisfied,

then

$\gamma$ is

calleda convex

_integrand.

The notion ofconvex

_integrand

was

_firstly

introduced

_by

J.

_Taylor

in

_[12]

and it

_plays

a

_key

role for

studying

Wulff

shapes

(for

detailson convex

integrands,

seeforinstance

_[4,

_7, 12

Definition2

_([10])

Let $\gamma$:

S^{n}\rightarrow \mathbb{R}_{+}

beacontinuousfunction. Theconvexhull of

\mathrm{i}\mathrm{n}\mathrm{v}(\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}( $\gamma$))

iscalled dual

_{Wulff of}

_{\mathcal{W}_{ $\gamma$},}

denoted

_by

_{D\mathcal{W}_{ $\gamma$}.}

Themain_topicof thispaper isthe relations between WuIffshapesanditsduals.

2

_Properties

and

some

known results

Before

_{proceeding further,}

wefirst introducean

equivalent

definition of Wulff

shape, given

in

[10].

(1)

Id:\mathbb{R}^{n+1}\rightarrow \mathbb{R}^{n+1}

_\times\{1\}.

Let Id:\mathbb{R}^{n+1}\rightarrow \mathbb{R}^{n+1}

_\times\{1\}

be themapdefined

by

Id(x)=(x, 1)

.

(2)

_{\mathrm{a}_{N}:S_{N,+}^{n+1}\rightarrow \mathbb{R}^{n+1}}

\times\{1\}.

Denote the

point

_{(0, \ldots, 0,1)}

\in \mathbb{R}^{n+2}

_by

N. The set S^{n+1}

-H(-N)

is denoted

by

S_{N,+}^{n+1}

. Let

$\alpha$_{N} :

S_{N,+}^{n+1}

\rightarrow \mathbb{R}^{n+1} \times

\{1\}

be the central

_projection

relative toN,

namely,

$\alpha$_{N} isdefined as follows for

any

P=(P_{1}, \ldots, P_{n+1}, P_{n+2})\in S_{N,+}^{n+1}

:

$\alpha$_{N}

(

P\mathrm{l},\cdots_,

P_{n+1}

_,

P_{n+2}

)

=

(\displaystyle \frac{P_{1}}{P_{n+2}}, \ldots , \frac{P_{n+1}}{P_{n+2}}, 1)

.

(3)

_{$\Psi$_{N}:S^{n+1}-\{\pm N\}\rightarrow S_{N,+}^{n+1}.}

Next,

weconsider the_{mapping $\Psi$_{N}}:

S^{n+1}-\{\pm N\}\rightarrow S_{N,+}^{n+1}

,defined

by

$\Psi$_{N}(\displaystyle \overline{P})=\frac{1}{\sqrt{1-(N\overline{P})^{2}}}(N-(N\cdot\tilde{P})\tilde{P})

.

The_{mapping $\Psi$_{N}}wasintroducedin

[9],

has the

following intriguing properties:

1. Forany

\overline{P}\in S^{n+1}-\{\pm N\}

,the

equality

\overline{P}\cdot$\Psi$_{N}(\overline{P})=0

holds,

2. forany

\overline{P}\in S^{n+1}-\{\pm N\}

,theproperty

$\Psi$_{N}(\overline{P})\in \mathbb{R}N+\mathbb{R}\overline{P}

holds,

3. forany

\tilde{P}\in S^{n+1}-\{\pm N\}

,theproperty

N\cdot$\Psi$_{N}(\overline{P})>0

holds,

(4)

Spherical polar

transform.

Foranypoint

\overline{P}\in S^{n+1}

,let

H(\overline{P})

betheclosed

hemisphere

centeredat

\overline{P}

,

namely,

H(\overline{P})=\{\overline{Q}\in S^{n+1}|\overline{P}\cdot\overline{Q}\geq 0\},

where the dot in thecenterstandsforthe scalar

product

oftwo vectors

\overline{P}, \overline{Q}\in \mathbb{R}^{n+2}

. Foranynon‐empty

subset

\overline{W}\subset S^{n+1}

, thespherical polarset

of

\tilde{W}

,denoted

by

\tilde{W}^{\mathrm{o}}

,isdefinedasfollows:

\displaystyle \tilde{W}^{\mathrm{o}}=\bigcap_{\overline{P}\in\overline{W}}H(\overline{P})

.

for detailson

_spherical

_{polar set,} seefor instance

[3, 10]

Proposition

1

_([10])

Let $\gamma$: S^{n}

\rightarrow \mathbb{R}+

beacontinuousfunction. Let

graph

(

_$\gamma$

)

=

\{( $\theta$, $\gamma$( $\theta$)) \in \mathbb{R}^{n+1} -\{0\} | $\theta$ \in S^{n}\}

, where

( $\theta$, $\gamma$( $\theta$))

isthe

polar

plot expressionforapointof

\mathbb{R}^{n+1}-\{0\}

.

Then,

\mathcal{W}_{ $\gamma$}

ischaracterizedasfollows:

\mathcal{W}_{ $\gamma$}=Id^{-1}\circ$\alpha$_{N}

(

($\Psi$_{N}\circ$\alpha$_{N}^{-1}\circ Id

(graph

( $\gamma$)))^{\mathrm{o}}

₎

For anyWulff

shape

\mathcal{W}_{ $\gamma$}

,

by

Proposition 1,the dualWulff

shape

\mathcal{D}\mathcal{W}_{ $\gamma$}

cancharacterizedasfollows:

Proposition

2

_([10])

For any Wulffshape

\mathcal{W}_{ $\gamma$}

,the

following

isholds:

\mathcal{D}\mathcal{W}_{ $\gamma$}=Id^{-1}\circ$\alpha$_{N}(($\alpha$_{N}^{-1}\circ Id(\mathcal{W}_{ $\gamma$}))^{\mathrm{o}})

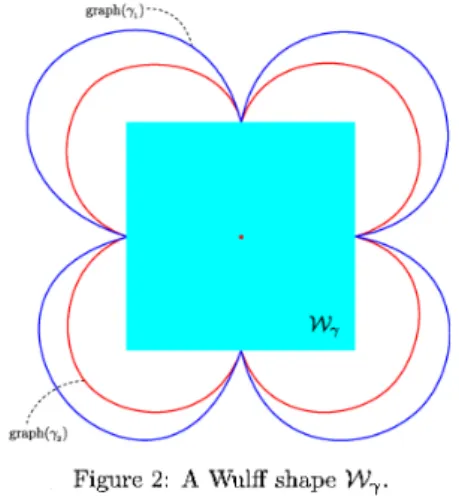
In

_general

case, for givenWulff_shape W, there exist uncountable many supportfunction $\gamma$ construct

W

_(see

_Figure

_2).

_Then, it is natural arise that “When does_given Wulff_shapehas _only one _support

fuction?). In

_[4],

it is shownthat Wulff

shape

Wis

_strictly

convexifand

only

if itsconvex

integrand

_$\gamma$

isof class C^{1}.

By

this

result,

\mathrm{e}the

following

theoremis notdifficult toprove.

Figure

2: AWulff

shape

\mathcal{W}_{ $\gamma$}.

Theorem 1

_([6])

Let $\gamma$: S^{n}

_{\rightarrow \mathbb{R}+}

beacontinuousfunction and let

_{\mathcal{W}_{ $\gamma$}}

be the Wulffshapeassociated with $\gamma$.

Suppose

For Wulff

shapes

andtheir dual Wulff

shapes,

wehave the

following

relations.

Proposition

3

_([4])

A Wulff

shape

in \mathbb{R}^{n+1} is

_strictly

convex ifand

_only

ifthe

_boundary

ofits dual Wulff

_shape

isC^{1}

diffeomorphic

toS^{n}.

Proposition

4

_([4])

A Wulfr

_shape

in\mathbb{R}^{n+1} is

_strictly

convexandits

boundary

isC^{1}

diffeomorphic

toS^{n} if and

_only

if jts dual Wulff

_shape

is

_strictly

convexand the

boundary

ofit isC^{1}

diffeomorphic

toS^{n}.

Proposition

5

_([10])

A Wulff

shape

in\mathbb{R}^{n+1} isa

polytope

ifand

only

ifitsdual Wulff

shape

isa

_polytope.

Deflnition3

_([2])

Let_{$\gamma$_{1}, $\gamma$_{2}}beconvex

_integrands.

Define_{$\gamma$_{7rax}} and_{$\gamma$_{ $\tau$ n\mathfrak{i}, $\iota$}} asnaturalway.

$\gamma$_{\max} :S^{ $\tau \iota$}\displaystyle \rightarrow \mathbb{R}+, $\gamma$_{rnax}( $\theta$)=\max\{$\gamma$_{1}( $\theta$), $\gamma$_{2}( $\theta$)\}.

$\gamma$_{rn}ỉ

$\iota$:S^{n}\rightarrow \mathbb{R}+,

$\gamma$_{ $\gamma$ nin}( $\theta$)=\displaystyle \min\{$\gamma$_{1}( $\theta$), $\gamma$_{2}( $\theta$)\}.

Proposition

6

_([2])

Let

_{\mathcal{W}_{$\gamma$_{1}},}

_{\mathcal{W}_{$\gamma$_{2}}}

be dual Wulff

_shapes.

Then

_{\mathcal{W}_{$\gamma$_{\ovalbox{\tt\small REJECT} rax}}}

is the dual Wulff

shape

of

_{\mathcal{W}_{$\gamma$_{\min}}.}

3

Self‐dual Wulff

_shapes

Definition 4

_([5])

Let W beaWulff

_shape.

If Wulff

_shape

W and itsdualWulff

_shape

are same convex

_body,

then W is

saidtobe

_self‐dual

Wulff

shape.

By Proposition 1,

wehave the

following.

Corollary

1

Let

_{$\gamma$:S^{n}\rightarrow \mathbb{R}+}

beacontinuousfunction. Then the

following

are

equivalent.

1.

_{\mathcal{W}_{ $\gamma$}=\mathcal{D}\mathcal{W}_{ $\gamma$}.}

2.

\mathcal{W}_{ $\gamma$}=Id^{-1}\mathrm{o}$\alpha$_{N}(($\alpha$_{N}^{-1}\mathrm{o} Id (\mathcal{W}_{ $\gamma$}))^{\mathrm{o}})

3.

_{\mathcal{W}_{ $\gamma$}}

is

_exactly

theconvexhullof

i\mathrm{n}\mathrm{v}(g\mathrm{r}\mathrm{a}ph( $\gamma$))

.

Moreover,

self‐dual Wulff

_shape

cancharacterizedasfollows.

Definition5 \hat{}

Ỉ[3])

1. A subset W ofS^{n+1}issaidtobe

_{hemispherical}

if there existsa

point

\tilde{P}\in S^{n+1}

such that

\tilde{W}\cap H(\tilde{P})=

\emptyset.

2. A

_{hemispherical}

subset

\tilde{W}

\subset S^{n+1} is said tobe

spherical

convexif for_any

\tilde{P}, \tilde{Q}\in

\tilde{W}

the

following

arc

\tilde{P}\tilde{Q}

iscontainedin

\tilde{W}

:

\displaystyle \overline{P}\overline{Q}=\{\frac{(1-t)\overline{P}+t\overline{Q}}{||(1-t)\tilde{P}+t\tilde{Q}||} | t\in[0, 1]\}

3. A

hemispherical

subset

\tilde{W}

iscalleda

_spherical

convex

_body

ifit is

_{closed, spherical}

convexand hasan

interior

point.

A

_hemisphere

H(\tilde{P})

issaidto_supporta

spherical

convex

body

\tilde{W}

if both

\tilde{W}\subset H(\tilde{P})

and

\partial\tilde{W}\cap\partial H(\overline{P})\neq\emptyset

hold.

Definition6

_{([8\lrcorner)_{-}}

1. Foranytwo

_P,

_{Q\in S^{n+1}}

(\tilde{P}\neq\pm Q

theintersection

H(\tilde{P})\cap H(\tilde{Q})

iscalledaluneofS^{n+1}.

2. The thickness

_of

the lune

H(\tilde{P})\cap H(\tilde{Q})

,denoted

by

\triangle(H(\overline{P})\cap H(\tilde{Q}))

, isthe real number

$\pi$-|\tilde{P}\tilde{Q}|,

where

_{|\tilde{P}\tilde{Q}|}

stands for the

_length

of thearc

\tilde{P}\tilde{Q}.

3. Fora

spherical

convex

_body

\tilde{W}

and a

_hemisphere

H(P)

_supporting

\tilde{W}

,the width

of

\tilde{W}

determined

by

H(P

denoted

_by

\mathrm{w}\mathrm{i}\mathrm{d}\mathrm{t}\mathrm{h}_{H(\tilde{P})}\tilde{W}

,istheminimumof the

following

set:

{

$\Delta$(H(\tilde{P})\cap H(\tilde{Q}))

_{|\tilde{W}\subset H(\tilde{P})\cap H(\tilde{Q})}

,

H(\tilde{Q})

supports

\tilde{W}

}.

4. _{For any}

_{$\rho$\in \mathbb{R}_{+}}

less than $\pi$,a

spherical

convex

body

\tilde{W}\subset S^{n+1}

is saidtobe

of

constantwidthpif

\mathrm{w}\mathrm{i}\mathrm{d}\mathrm{t}\mathrm{h}_{H(\tilde{P})}\tilde{W}= $\rho$

for_any

_H(P)

_supporting

\tilde{W}.

Theorem 2

_([5])

Let $\gamma$: S^{n} \rightarrow

_\mathbb{R}+

be acontinuousfunction.

Then,

the Wulff

shape

W_{ $\gamma$}

is self‐dual if and

_only

if the

spherical

convex

body

\tilde{W}_{ $\gamma$}=$\alpha$_{N}^{-1}\mathrm{o}Id(W_{ $\gamma$})

isofconstantwidth

_$\pi$/2.

Definition7

_([8])

Let

\tilde{W}

bea

spherical

convex

body

ofS^{n+1}

1. Thickness

$\Delta$(\tilde{W})

of

\tilde{W}\subset S^{n+1}

definedasfollows:

$\Delta$(\displaystyle \tilde{W})=\inf\{width_{K}(\tilde{W});K

isa

_{supporting hemisphere}

of W

2.

\tilde{W}\subset S^{n+1}

issaidtobe reducedif

$\Delta$(\ovalbox{\tt\small REJECT})< $\Delta$(\tilde{W})

for_everyconvex

body

Ỹ

\subsetW

\tilde{}

different from

\tilde{W}.

Theorem 3

_([8])

Every

smooth reduced

_body

onS^{n} is ofconstantWidth.

Inthecaseof Wulff

_shapes,

the

following

seemstobeopen.

Definition8

_([8])

Let

\tilde{W}\subset S^{n+1}

bea

_spherical

convex

_{body. Then,}

the

_following

numberiscalled the diameter of

\tilde{W}

and isdenoted

_by

diam

(\tilde{W})

:

\displaystyle \max\{|\tilde{P}\tilde{Q}| |\tilde{P}, \tilde{Q}\in\tilde{W}\}.

Question:

Let W be aWulff

shape.

Are the

_{following equivalent?}

1. Wulff

shape

W is self‐dual.

2.

_Spherical

convex

_body

\tilde{W}_{ $\gamma$}=$\alpha$_{N}^{-1}\mathrm{o}Id(W_{ $\gamma$})

isreduced and diam

(\tilde{W})= $\pi$/2.

References

[1]

Y.

_{Giga, Surface}

Evolution

_{Equations, Monographs}

of

Mathematics,

99,

Springer,

2006.

[2]

H.

_Han,

Maximum and minimum _operators

_of

convex

integrands,preprint

(available

from

arXiv:arXiv: 1701.08956.

[3]

H.Han andT.

_Nishimura,

The_spherical dual

transform

is an_isometry

for spherical Wulff shapes,

[4]

H. Han andT.

_{Nishimura, Strictly}

convex

Wulff shapes

andC^{1} convex

integrands,

to appear in

Proceedings

of theAMS

_(available

from arXiv:1507.05162

_[math.MG]).

[5]

H. Han andT.

_{Nishimura, Self‐dual Wulff shapes}

and

spherical

convexbodies

_of

constantwidth

_$\pi$/2,

to appear inJournal of the mathematical

society

of

Japan

[6]

H. Han andT.

_Nishimura,

_Spherical method

for studying Wulff

shapesand related_topics,

_accepted

for

_publication

in

_Proceedings

of

_{Singularities}

inGeneric

_Geometry

and its

_{Applications Kobe‐Kyoto}

2015

_(Valencia

IV

[7]

F.

_Morgan,

The coneoverthe

_Clifford

torus in\mathbb{R}^{4} \dot{u} $\Phi$

_{‐minimizing,}

Math.

_Ann.,

289

_(1991),

341−

354.

[8]

M.

_Lassak,

Widthof

spherical

convex

bodies,

Aequationes Math.,

89

(2015)

555‐567.

[9]

T.

_Nishimura,

Normal

forms for singularities of pedal

curves

_{produced by non‐singular}

dualcurve

germs in S^{n},Geom Dedicata

133(2008),

59‐66.

[10]

T. Nishimura and Y.

_{Sakemi, Topological}

aspect

of Wulff shapes,

J. Math. Soc.

Japan,

66

_(2014),

89‐109.

[11]

A.

_Pimpinelli

and J.

_{Villain, Physics of Crystal Growth, Monographs}

and TextsinStatistical

Physics,

Cambridge University Press, Cambridge

New

_York,

1998.

[12]

J. E.

_{Taylor, Crystalline}

variational

problems,

Bull.Amer. Math.

_Soc.,

_84(1978),

568‐588.

[13]

J. E.

_Taylor,

J. W. CAn and C. A.

_Handwerker,

Geometric models

_{of crystal growth,}

Acta Metal‐

lurgica

et

Materialia,

40(1992),

1443‐1474.

[14]

G.

Wulff,

Zur

frage

der

geschwindindigkeit

des wachstrums und der

_auflösung

der

_{krystallflachen,}

Z.