GPUのキャッシュを考慮した疎行列ベクトル積計算手法の性能評価

全文

(1)Vol.2014-HPC-144 No.5 2014/5/26. 情報処理学会研究報告 IPSJ SIG Technical Report. GPU のキャッシュを考慮した疎行列ベクトル積計算手法の性能評価長坂侑亮1,a). 額田彰1. 松岡聡1. 概要：巨大な疎行列を係数行列として持つ連立一次方程式を解く際，疎行列ベクトル積計算が実行時間の大部分を占める．GPU などのメニーコアプロセッサはキャッシュ容量が小さいため，入力ベクトル要素へのランダムアクセスによって多数のキャッシュミスが生じる．そのため疎行列ベクトル積計算性能は著しく低い．我々はメニーコア環境においても高いキャッシュヒット率を達成するために，行列を列方向で分割することで各処理内での入力ベクトル要素の再利用性を向上させたフォーマットと疎行列ベクトル積カーネルを新たに提案する．Florida のデータセットから選出した行列に対して既存手法との比較を行った．その結果，疎行列ベクトル積計算について 2.0 倍，CG 法について 1.12 倍の性能向上を果たした．. 1. はじめに. 時間の大部分を占める疎行列ベクトル積計算は，その性能低下の特徴を顕著にあらわしている．これは疎行列を圧縮. GPU などのメニーコアプロセッサは多くのコアを一つ. したことにより，疎行列ベクトル積計算において入力ベク. のチップに収めており，これらのコアと高いバンド幅を有. トル要素へのランダムアクセスが発生することによるもの. するメモリを効果的に用いることによって高い演算性能. である．一般的な CPU に対しては疎行列ベクトル積計算. を実現している．それに加えて一般的なマルチコアアー. の性能向上が図られている一方，GPU などのメニーコア. キテクチャから電力の点においても優位性がある．GPU. プロセッサーに対しては，ランダムアクセスに対するハー. アーキテクチャでは，それぞれのスレッドが別々のデータ. ドウェア的サポートが欠けていることとキャッシュの容量. に対して同じ計算を行うが，従来のベクトル計算機と異. が小さいために，GPU のリソースを十分に活用した解決. なり実行順番がより柔軟になっている．また GPU は深い. 策は示されていない．. キャッシュ階層は持っていないが，たとえば shared メモ. 本論文において我々は，容量の小さいキャッシュしか持. リのように小さいながらもいくつかのオンチップメモリを. たないメニーコアプロセッサーに対して，入力ベクトル要. 持っており，これらのメモリを効果的に用いることと SMT. 素のキャッシュでの再利用性を向上させることで性能向上. （Simultaneous Multi-Threading）機能を組み合わせること. を図った新たなフォーマットとそれに基づいた疎行列ベク. で，レイテンシ隠蔽を可能としている．. トル積カーネルを提案する．Florida 大学の Sparse Matrix. しかしながら未だ多くのコードやアルゴリズムが一般的. Collection[4] から選出した行列データに対して，メニーコ. な CPU 向けへの最適化となっており，GPU への移植を行. アで高い性能を発揮する SELL-C-σ などの従来手法と比較. う場合もステンシル計算のようにメモリアクセスが単純で. して，疎行列ベクトル積計算で最大 2.0 倍，CG 法で最大. 規則正しいならば高い性能を出すことに成功している [1]. 1.12 倍の性能向上を果たした．. 一方，計算カーネルがランダムメモリアクセスや間接参照を含む場合には性能が大きく低下する．ランダムアクセスに対するハードウェア的なサポートが欠けているために，ランダムアクセスはメニーコアアーキテクチャにおける致. 2. 背景 2.1 CG 法有限要素法などの離散化手法によって生成される巨大な. 命的な弱点となっている．特に CG（Conjugate Gradient）. 疎行列を係数行列として持つ連立一次方程式を解くこと. 法やページランクアルゴリズム [2]，[3] などにおいて実行. が，科学技術計算においてしばしば求められる．そのような方程式を効果的に解く手法として，反復法が知られてお. 1. a). 東京工業大学 Tokyo Institute of Technology nagasaka.y.aa@m.titech.ac.jp. ⓒ 2014 Information Processing Society of Japan. り，特に係数行列が正定値対称行列である場合には CG 法が用いられる．CG 法は AXPY やドット積という level-1. 1.

(2) Vol.2014-HPC-144 No.5 2014/5/26. 情報処理学会研究報告 IPSJ SIG Technical Report. BLAS と疎行列ベクトル積計算から成り立っている．多く. ベクトル計算機においては，行列要素の読み込みは連続. のアーキテクチャにおいて，連続アクセスからなる level-1. でまとまった単位で行われ，入力ベクトルの読み込みは. BLAS は効果的に処理が行われるが，疎行列ベクトル積計. gather 操作を，出力ベクトルへの書き込みは scatter 操作を. 算は入力ベクトル要素へのランダムアクセスにより多くの. 用いる．しかし，昨今用いられているメニーコアアーキテク. キャッシュミスが発生するため，性能が著しく低い．CG. チャの多くは連続アクセスに特化しており，gather-scatter. 法全体における疎行列ベクトル積計算の割合は 90%を超え. 操作のコストが大きい．そのため，このようなアーキテク. ることもあり，疎行列ベクトル積計算の性能は CG 法の性. チャ上では疎行列ベクトル積計算の性能は芳しくない．. 能に直結するため，現在まで多くの疎行列ベクトル積計算の高速化研究がなされてきた [5]，[6]，[7]，[8]．. 我々は GPU における JDS フォーマットによる疎行列ベクトル積について，入出力ベクトルのリオーダリングを行うことによって，scatter 操作の削減を行った．図 2 にリ. 2.2 既存の疎行列フォーマット. オーダリング操作を示す．CG 法などにおいて，繰り返し. 科学技術計算において生成される行列のサイズが巨大. 疎行列ベクトル積が用いられる際，前処理として入出力ベ. になっていくものの，その要素の多くが処理には関係の. クトルのリオーダリングを行うことで各反復中は連続で書. ないゼロ要素である．そのような行列をどのように圧縮. き込みを行えるようにし，反復が完了した段階で再びベク. して扱うか，というのが疎行列フォーマットの基本的な. トルのオーダリングを戻す．この手法により，JDS フォー. 考えである．既存のフォーマットとして，広く知られてい. マットを用いた場合の疎行列ベクトル積計算の処理時間を. るものとして COO と CSR がある．COO（Coordinated）. 短縮することが可能となり，特にサイズの大きい行列に対. フォーマットは行列の非ゼロ要素に関してのみ，値，列イン. しては大きな効果がある．. デックス，行インデックスを保持する．CSR（Compressed. 2.2.2 ELLPACK フォーマットとその拡張. Sparse Row）フォーマットは各行ごとに圧縮を行い，行. ELLPACK フォーマットもベクトル計算機やメニーコア. インデックスの代わりに各行の開始オフセットを保持する. プロセッサにおいて効果的に処理を行うためのフォーマッ. ことで COO と比較してメモリ使用量を削減している．昨. トである．行方向に関して圧縮を行った後，メモリ配置を. 今，疎行列ベクトル積計算において特定の行列やアーキテ. column-major にするために各行の非ゼロ要素数を揃える. クチャに対してより高い性能を出すために，多くの疎行. ことを目的としたパディングを行う．行あたりの非ゼロ要. 列フォーマットが提案されている [9]，[10]，[11]．例えば，. 素数について，各行ごとの差がない場合においてはパディ. 対角行列に近い行列に対して有用な DIA フォーマットと. ングの量が少ないため ELLPACK は効果的であるが，差. ELL フォーマット，ベクトル計算機に対して最適化された. が大きい場合は性能が低下する．これを解決するためにい. JDS フォーマットが挙げられる．JDS フォーマットはベク. くつかの ELLPACK フォーマットの拡張が提案されてい. トル計算機だけでなく，GPU に対しても有用であること. る [14]，[15]．. が示されている [12]，[13]．しかし，これらのフォーマット. Moritz Kreutzer によって SELL-C-σ フォーマット [16]. は行列の性質によって，性能が大きく変化する．. が提案された．図 3 に SELL-C-σ の例を示す．σ 行ごとに. 2.2.1 JDS フォーマット. 非ゼロ要素数に応じてソーティングした後に，C 行ごとに. はじめに CSR のように各行ごとに圧縮を行い，各行の. ELLPACK への変換を行う．C 行ごとという細かいブロッ. 非ゼロ要素数に応じて行列のソーティングを行う．その. ク単位で変換を行うので，非ゼロ要素数の多い行が存在す. 結果，図 1 のように非ゼロ要素数の多い行が上に集まる．. る場合でもその行の影響が及ぶ範囲を狭くすることができ，. JDS ではこれを column-major でのメモリ配置で扱う．. ソーティングによって更に効果的にパディングの量を減らしている．パラメータ C はアーキテクチャの特徴に依存しており，NVIDIA の GPU を用いる場合には WARP サイズ（= 32）に合わせている．σ は元の行列の特徴を失わない程度に設定する必要があり，著者らは σ = 256 程度が良いと記している．. Nathan Bell らによって，ELLPACK と COO の二つを結合した Hybrid フォーマット [17] が提案された．基本的には ELLPACK で構築し，非ゼロ要素数の偏った部分を. COO で構築することでパディングの量を減らしている．このフォーマットは CSR と同様に NVIDIA の cuSPARSE ライブラリ [18] に実装されており，どの程度の部分を ELL図 1. JDS フォーマット. ⓒ 2014 Information Processing Society of Japan. PACK で構築するのかという最も重要であるパラメータの. 2.

(3) Vol.2014-HPC-144 No.5 2014/5/26. 情報処理学会研究報告 IPSJ SIG Technical Report. !"#$%&!. )*"#+*#,%&!. '(!!. 図 2. JDS フォーマットに対する入出力ベクトルのリオーダリング. • 行数 : 4M • 行あたりの非ゼロ要素数 : 16 • 列数 : 2 のべき乗で変化させる • 列インデックスをランダムに設定なお，実験には NVIDIA の Tesla K20X を用い，read-only キャッシュは入力ベクトルに対してのみ適用した．フォーマットは入出力ベクトルのリオーダリングを行った JDS フォーマットを用いた．図 4，5 に列数を変化させた時の !"##$%$'!. !"##$%$&! 図 3. 性能とキャッシュヒット率のグラフを示す．. SELL-C-σ フォーマット. 32. 64. 128. 256. 512. 25. 設定も含めて Hybrid フォーマットに変換するサブルーチ. 3. 提案. 20 GFLOPS!. ンが提供されている．. 15 10 5. 3.1 列数とキャッシュヒット率の関係これまで様々なフォーマットが提案されてきたが，いず. 0 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 Column Size (pow(2, x))!. れのフォーマットについても GPU における行列要素へのアクセス効率化は行われているものの，入力ベクトル要素. 図 4. 列数と性能の関係. へのランダムアクセスによって引き起こされるキャッシュヒット率低下の問題が依然として残っている．キャッシュ. スレッドブロック内のスレッド数を 32，64，128，256，. ミスが増えることにより，パイプラインストールが多く発. 512 と設定しており，スレッド数が 32 の時はスレッド数. 生し，メモリアクセスのレイテンシの隠蔽が困難になる．. が少ないためにレイテンシの隠蔽が効果的に行われておら. 疎行列ベクトル積におけるキャッシュヒット率が性能に. ず，性能は 11GFlops 程度が上限となっている．一方，ス. 与える影響を分析するために予備実験を行った．以下の条. レッド数を 64 以上とした場合には，列数を増加させる過程. 件で行列をランダム生成した．. で二つの大きな性能低下のポイントがある．この二つのポ. ⓒ 2014 Information Processing Society of Japan. 3.

(4) Vol.2014-HPC-144 No.5 2014/5/26. 情報処理学会研究報告 IPSJ SIG Technical Report. る．第二段階では一時的に書き込んだ領域から適宜読み込 Read-only. L2. み足し合わせることで，最終的な出力ベクトルを得る．第. Cache Hit Rate!. 100 80. 一段階での書き込みは連続書き込みであるため，各部分行. 60. 列ごとにソーティングを行っている場合には対応する順番. 40. が異なる．そのため第二段階における各部分行列の計算結. 20. 果へのアクセスはランダムである．. 0 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 Column Size (pow(2, x))!. Segmented フォーマットでは列方向の分割を行うことによって，第一段階でのキャッシュヒット率向上を図れるが，各部分行列の一時的なメモリ格納によって発生する連続書. 図 5 列数とキャッシュヒット率の関係. き込み，第二段階で発生するランダム読み込みやそれらを. イントはそれぞれ read-only キャッシュと L2 キャッシュ. 間接参照するための配列へのアクセスが余分に増えるとい. のサイズに対応している．. う問題もある．しかし第二段階で発生するランダムアクセ. これらの結果から，入力ベクトル要素へのアクセス範囲. ス数は高々 N × 分割数であるため，非ゼロ要素の割合の高. を制限することができれば，高いキャッシュヒット率と性. い行列においては致命的な性能低下の要因とはならない．. 能を達成することが可能になると考えられる．この考えに. Segmented フォーマットでは第一段階でのキャッシュヒッ. 基づき，我々は行列を列方向で分割する新たなフォーマッ. ト率向上と分割によって発生するメモリアクセスの増加の. トと疎行列ベクトル積計算手法を提案する．行列を列方向. トレードオフを取ることが重要であると言える．. で分割することに伴い，入力ベクトルはそれに合わせた部分ベクトルへと分割されるため，ランダムアクセスされ. 3.3 Non-Uniformly Segmented フォーマット. る範囲を制限し，キャッシュヒット率を向上させること. Segmented フォーマットでは一つの分割幅に基いて列方. が可能になる．分割後の各部分行列はそれぞれ GPU に適. 向分割を行っていたが，実際の行列では非ゼロ要素が均. したフォーマットにする必要があり，本論文では JDS と. 等に配置されていることは少ないため，Segmented フォー. SELL-C-σ への変換を行った．. マットではメモリアクセス量が少ない部分行列が生み出されていた．このような部分行列はキャッシュミスがそもそも少ないため恩恵が小さい．これを解消するために，. 3.2 Segmented フォーマット Segmented フォーマットでは分割幅を一つ設定し，その. 非ゼロ要素数の多いエリアは細かく分割し，少ないエリ. 値に基いて均等な列方向分割を行う．分割後の各部分行列. アには粗い分割を行えるようにした NUS（Non-Uniformly. は JDS や SELL-C-σ などのメニーコアアーキテクチャへ. Segmented）フォーマットを新たに提案する．このフォー. の親和性が高いフォーマットへと変換する．図 6 に S-JDS. マットでは複数の分割幅と分割数を設定可能とし，非ゼロ. フォーマットを用いての疎行列ベクトル積計算の手法を示. 要素数が多いエリアは細かく分割することにより高速なア. す．Segmented フォーマットを用いての疎行列ベクトル積. クセスが可能であるキャッシュでの再利用性を高め，非ゼ. 計算は二つの段階から成る．第一段階では各部分行列と部. ロ要素数が少ないエリアは粗い分割を行うことで，低速で. 分ベクトルに対して疎行列ベクトル積計算を行い，計算結. はあるもののより容量が大きいキャッシュでの再利用性を. 果は各セグメントごとに別々のメモリ領域に書き込まれ. 保ちつつ，分割数を減らすことを可能としている．我々の. !"#$%&'()*'+),%$) 図 6 SJDS フォーマットでの疎行列ベクトル積計算. ⓒ 2014 Information Processing Society of Japan. 4.

(5) Vol.2014-HPC-144 No.5 2014/5/26. 情報処理学会研究報告 IPSJ SIG Technical Report 表 1 Matrix. 実験に用いた University of florida の Sparse Matrix Collection の行列. Number of rows. Number of non-zero elements. 943,695. 77,651,847. structural problem. 82.28. nd12k. 36,000. 14,220,946. 2D/3D problem. 395.02. crankseg 2. 63,838. 14,148,858. structural problem. 221.63. crankseg 1. 52,804. 10,614,210. structural problem. 201.01. nd24k. 72,000. 28,715,634. 2D/3D problem. 398.83. mouse gene. 45,101. 28,967,291. undirected weighted graph. 642.28. F1. 343,791. 26,837,113. structural problem. 78.06. F2. 71,505. 5,294,285. structural problem. 74.04. 141,347. 7,339,667. structural problem. 51.93. 84,414. 13,135,930. power network problem. 155.61. 503,712. 36,816,342. structural problem. 73.09. audikw 1. bmw7st 1 TSOPF FS b300 c3 inline 1. 提案する NUS フォーマットでは以下の式に基いて分割を行った．. N = S1 × K1 + S2 × K2 + S3. Application info. 0. 0. 1. (1). S1 と S2 は分割幅を，K1 と K2 は分割数を表し，S3 は行列を分割しても効果が薄いエリアの列数である．非ゼロ要素. Number of non-zero elements per row. 2. 4. 1. 2. 0. 3. 0. 4. 0. 5. 0. 1. フォーマットの変換手順を記す．. ( 1 ) 各列の非ゼロ要素数に応じて行列のソーティングを行う．. ( 2 ) 入力ベクトルのリオーダリングを行う．アクセス回数. 2 3. 4. 3. 4. 5. 4. 4. 5. 5. 0. 4. 1. 4. 2. 0. 5. 2. 4. 0. 4. 4. 0. 5. 5. 4. 0. 5. 0. 1. 0. 1. 4. 性能評価我々が提案する分割フォーマットと，既存のフォーマットとの比較を行った．比較は Flops 値性能を基に行い，Flop. 3. 3. 4 5. 2. 1. 2. 4. 4. 3 1. 0 4. 3. 0. 0. 4. 0. 1. 2. 5. 0. 1. 2. 3. 5 5. 1. 5. 2 3. (3)Reordering,rows,, and,output,vector. オーダリング操作を無くすことができる．それぞれ JDS に変換する．. 2 3. (2)Reordering,input,vector 0. ( 4 ) 分割幅と分割数に基いて行列を分割し，各部分行列を. 1 2. 3. 行う．. いて繰り返し疎行列ベクトル積計算を行う場合のリ. 0. 1 0. まる．これに合わせて行列の列インデックスの更新も. ルのオーダリングを揃える．CG 法などの反復法にお. 3. (1)Reordering,columns. の多い入力ベクトル要素がベクトルの上の部分に集. ( 3 ) 入力ベクトルのオーダリングに合わせて，出力ベクト. 0 1. 2. 数の多いエリアと少ないエリアを分けるために，入出力ベクトルのリオーダリングを行っている．図 7 に NUS-JDS. 5. 4. 4. 0. 1. 2. 0. 0. 1. 2. 5. 0. 1. 2. 1. 0. 2 3. 3. 4 0 5. 3 1. 0. 5 4. 1 4. 0. 2 5. 3. (4)Segmen;ng,by,columns,, and,conver;ng,into,JDS. 値は疎行列ベクトル積の場合は (2 * nnz) を，CG 法は (2. * nnz + 11 * N) に反復数をかけたものとした．nnz は行. 4. 0. 1. 2. 3. 列の非ゼロ要素数，N は行列の一辺サイズを表す．また，. 0. 0. 1. 2. 4. 0. 5. 0. 1. 2. 3. 5. 1. 0. 1. 4. 1. 2. 0. 5. 2. すべての実験は単精度で行った．実験に用いた行列は University of Florida の Sparse Ma-. trix Collection[4] から選択した．表 1 に用いた行列を記す．. 3. 5. 4. 3. これらの行列は対称行列であり，既存手法における疎行列ベクトル積計算において性能値が低い傾向にあったものである．. 図 7. NUS-JDS フォーマットへの変換手順. キャッシュを共有し，各 SMX に 48KB の read-only キャッ. 実験には NVIDIA の Tesla K20X が搭載された. シュを有する．実際には read-only キャッシュは 4 つにわ. TSUBAME-KFC を用いた．GPU は最大 260GB/sec の. かれており，それぞれのサイズは 12KB である．Read-only. 帯域幅である容量 6GByte のメモリを持ち，これに加え. キャッシュはランダムアクセスが発生する入力ベクトル要. て Kepler 世代の GPU では 14 の SMX で 1.5MByte の L2. ⓒ 2014 Information Processing Society of Japan. 5.

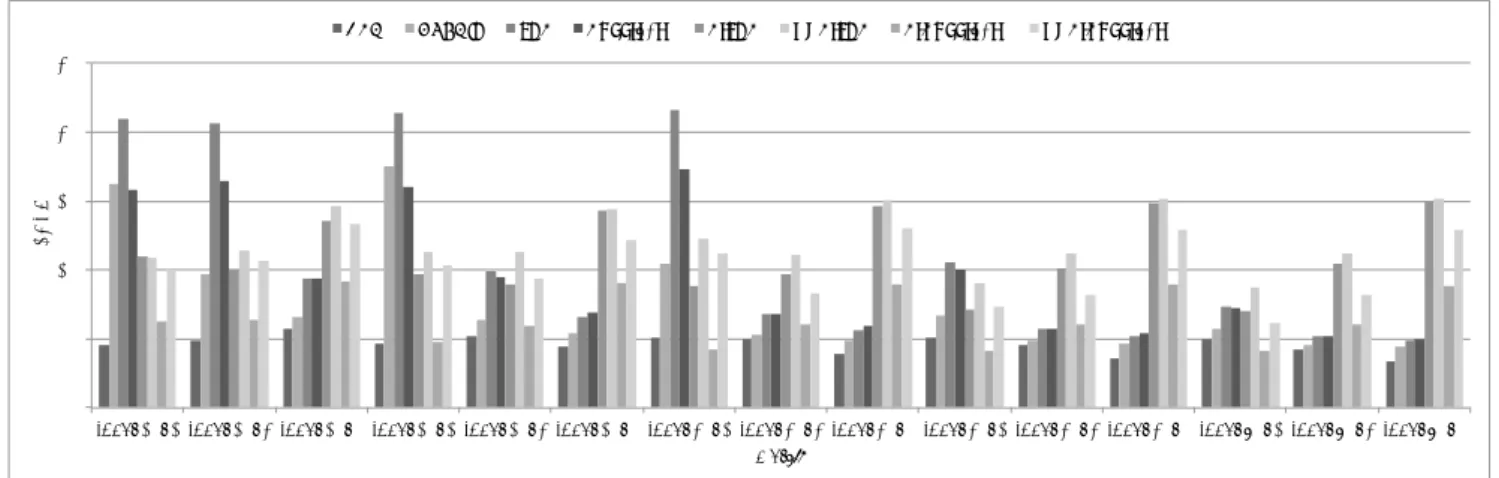
(6) Vol.2014-HPC-144 No.5 2014/5/26. 情報処理学会研究報告 IPSJ SIG Technical Report. 1>C". DEFCGH". IH>". >JKKL%$LM". >LIH>". NO>LIH>". >L>JKKL%$LM". NO>L>JKKL%$LM". (!". '!". !"#$%&!. &!". %!". $!". #!". !" )*+,-./#". 0+#$-". 1230-456/$". 1230-456/#". 図 8. 0+$&-". 78*45/6505" '()*+,!. 9#". 9$". :7.;4</#". =>?@9/9>/:%!!/A%". ,0B,05/#". Florida 大学の行列データに対する疎行列ベクトル積性能. 素に対してのみ適用している．コードは CUDA 5.5 で実装. キングを行っており，それぞれキャッシュヒット率の向上. されており，CentOS Linux 6.5 OS 64bit 環境のもと実行. が見られる．ただし，TSOPF FS b300 c3 の行列だけは例. された．. 外であり，分割を行わない状態での Read-only キャッシュヒット率が十分に高い．これは非ゼロ要素数が極端に多い. 4.1 疎行列ベクトル積計算. 箇所があるために，その部分でのヒット率が高くなるこ. 図 8 に疎行列ベクトル積計算の性能を示す．疎行列ベク. とによるものである．分割系フォーマットは偏った部分. トル積計算の性能比較として，NVIDIA の cuSPARSE ラ. を分割して列方向に関して並列処理することで，JDS や. イブラリで提供されている CSR フォーマットと HYBRID. SELL-C-σ からの性能向上を果たした．. フォーマットに加え，分割を行わない元の状態の JDS と. SELL-C-σ の評価も併せて行った．一方，我々の提案す. HIB". と SELL-C-σ の両方を適用し，合計 4 つのフォーマットに対して評価を行った．分割系フォーマットである S シリーズと NUS シリーズの分割幅，分割数は表 2 に記した設定で行った．部分行列を SELL-C-σ に変換した場合のパラメータ設定は C=32，σ = 25600 とした．結果として，. !"#$%&'()&*")%&+,-!. る S シリーズと NUS シリーズに対してはそれぞれに JDS. BJ,,1<1K". BHIB". LMBHIB". #!!" +!" *!" )!" (!" '!" &!" %!" $!" #!" !" ,$". NUS-SELL-C-σ が全体的に高い性能値を示しており，既存. -./012345". ,$". 67089:;#". -./012345". <=/39>.?;$". ,$". -./012345". @27>.;?.3.". ,$". -./012345". ABCDE;EB;F%!!;G%". 手法の 4 つと比較して最大で 2.0 倍の性能向上を果たした．図 9 Florida の疎行列データに対する疎行列ベクトル積計算での表 2. 各行列に対する最適な分割数と分割幅分割幅は列数を表す. Matrix. Uniformly Segmented. Non-uniformly Segmented. 256k. 128k*2+665k. nd12k. 2k. 2k*10+3k*5. crankseg 2. 1k. 3k*16+4k*5. crankseg 1. 1k. 2k*26. nd24k. 3k. 3k*24. mouse gene. 1k. 1k*35+2k*5. F1. 512k. 128k*1+207k. F2. 32k. 32k*2+6k. bmw7st 1. 32k. 16k*3+90k. 1k. 1k*40+8k*5. 256k. 128k*1+363k. audikw 1. TSOPF FS b300 c3 inline 1. キャッシュヒット率. 我々の提案が実効バンド幅という点においてどの程度の最適化がほどこされているのかの検証を行った．ベクトル計算機では NEC の SX-8 のようにキャッシュを持っていないものもある．このようなアーキテクチャの場合，疎行列ベクトル積は (3 ∗ nnz + 2 ∗ N )×sizeof(float and int) bytes のメモリアクセスを要求する．表 3 に NUS-SELL-C-σ フォーマットを用いた際のメモリバンド幅を算出したものを記す．最大で 284GB/sec を記録しており，これは NEC の SX-6. 図 9 に各フォーマット毎のキャッシュヒット率を示す．サイズの小さい行列においては read-only キャッシュに対する，大きい行列においては L2 キャッシュに対するブロッ. ⓒ 2014 Information Processing Society of Japan. のピークバンド幅である 256GB/sec を超えるものとなっている．我々の提案する疎行列フォーマットがサイズの大きい. 6.

(7) Vol.2014-HPC-144 No.5 2014/5/26. 情報処理学会研究報告 IPSJ SIG Technical Report. CSR. HYBRID. JDS. SELL-32-σ. S-JDS. NUS-JDS. S-SELL-32-σ. NUS-SELL-32-σ. 25. GFLOPS!. 20. 15. 10. 5. 0 rand_10_1 rand_10_2 rand_10_5 rand_15_1 rand_15_2 rand_15_5 rand_20_1 rand_20_2 rand_20_5 rand_25_1 rand_25_2 rand_25_5 rand_30_1 rand_30_2 rand_30_5 Matrix!. 図 10 表3. ランダム生成した行列に対する疎行列ベクトル積性能. NUS-SELL-C-σ フォーマットを用いた場合の疎行列ベクトル. 先の評価で用いたものと同じものを，ドット積と AXPY. 積処理中のメモリバンド幅. の処理には cuBLAS を用いた．なお，用いる行列は疎行. Matrix. Bandwidth. audikw 1. 267.5. nd12k. 238.9. crankseg 2. 190.0. crankseg 1. 166.7. nd24k. 236.9. mouse gene. 240.3. F1. 284.0. F2. 231.5. bmw7st 1. 196.9. TSOPF FS b300 c3. 112.5. inline 1. 278.7. 列ベクトル積計算で用いたものから，非正定値行列である’mouse gene’ と’TSOPF PF b300 c3’ を除いたものとなる．図 11 に示すように，CG 法でも疎行列ベクトル積と同様の性能変化を示しており，我々が提案したフォーマットは既存のフォーマットから最大 1.12 倍の性能向上を果たした．. 5. 関連研究行列に対しても有用であるかを確かめる必要性があるが，. Florida の疎行列コレクションではサイズが大きくかつ，ランダム性の高いものは少ない．そのため本論文ではサイズの大きい行列をランダム生成し，それに対して性能評価を行った．行列はサイズを 1M，1.5M，2M，2.5M，3M，非ゼロ要素密度を 0.0001%，0.0002%，0.0005%として生成した．この行列は対角成分に非ゼロ要素を配置してあり，それ以外の非ゼロ要素は対称行列であるという条件を満たすだけでランダムな配置となっている．図 10 にランダム生成した行列に対する疎行列ベクトル積の性能を示す．各行列の名前は’rand <サイズ> <密度>’ である．分割系フォーマットについて，分割幅は 256k で統一されており，NUS シリーズではそれに加えて分割数を適切なものに調整している．JDS や SELL-C-σ を用いた場合はサイズ，密度が共に小さい行列では高い性能が出ているが，サイズや密度が大きくなるにつれ性能が低下している．これに対し，L2 キャッシュでの再利用性を高めた分割系フォーマットではサイズや密度が増えた場合にも安定して高い性能を維持している．. 4.2 Conjugate Gradient 分割系フォーマットを用いることで疎行列ベクトル積の性能向上を確認したが，続いて CG 法においてどれだけの効果があるのかを評価した．疎行列ベクトル積部分は. ⓒ 2014 Information Processing Society of Japan. 疎行列ベクトル積計算における入力ベクトル要素へのランダムアクセスによって発生するキャッシュヒット率低下を抑えることを目的とした既存の研究について記す．疎行列ベクトル積計算における CPU に対するキャッシュブロッキング手法が Eun-Jin Im らによって提案された [19]．低いキャッシュヒット率を改善するために，彼らは小さいタイル状に行列を分割した．タイルのサイズは. 32K × 32K から 128K × 128K の中で最適なものを各行列に対し選択している．このブロッキングは入力ベクトルのみならず，出力ベクトルも考慮されている．しかし彼らが対象としているのは各コアあたり数スレッドの一般的な. CPU であり，各コアの L1 キャッシュ制御を行いやすい．一方，GPU など多量のスレッドが同時に動作している場合，多くのスレッドによって共有されているキャッシュの制御は飛躍的に困難となる．. GPU 向けのキャッシュブロッキングを行うための BCSR フォーマットと疎行列ベクトル積カーネルが Weizhi Xu らによって提案された [20]．この BCSR フォーマットは従来の BCSR フォーマットと異なり，パディングを行わない．彼らが対象としたのは Fermi 世代の GPU であり，分割サイズは入出力ベクトルの両方を考慮しつつ，L1 キャッシュに合わせたものになっている．疎行列ベクトル積計算において，我々の実装では各ブロックごとの出力をそれぞれ一時的にメモリに書き出しているのに対し，彼らの実. 7.

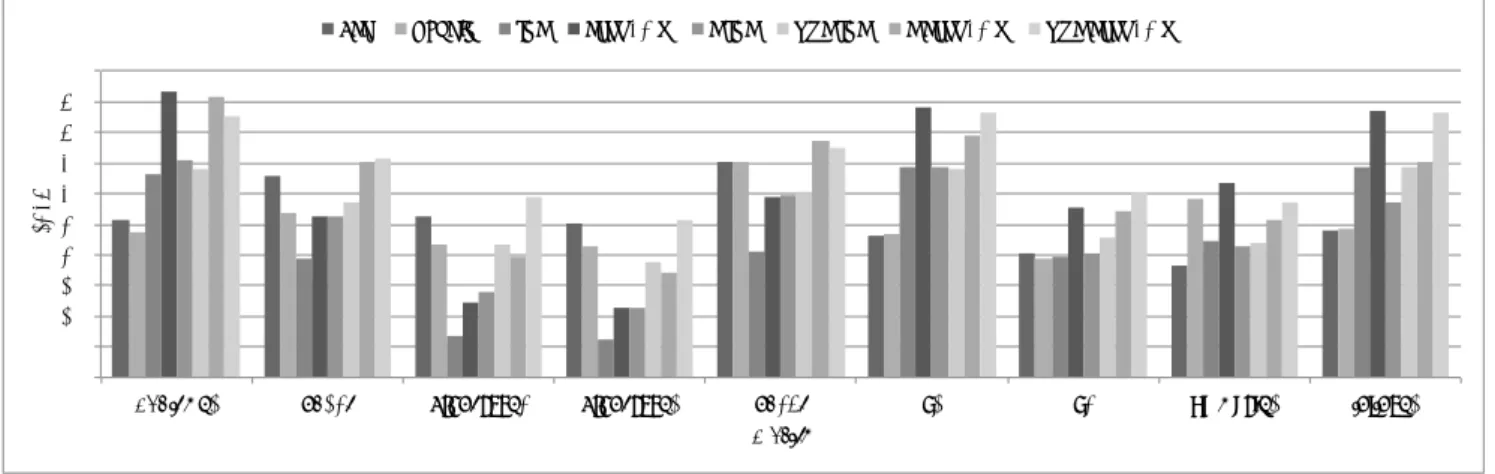
(8) Vol.2014-HPC-144 No.5 2014/5/26. 情報処理学会研究報告 IPSJ SIG Technical Report. !"#$%&!. 0<=". >?@=AB". CB<". <DEEF&%FG". <FCB<". HI<FCB<". <F<DEEF&%FG". HI<F<DEEF&%FG". #!" '#" '!" &#" &!" %#" %!" $#" $!" #" !" ()*+,-.$". /*$%,". 012/,345.%". 012/,345.$". 図 11. /*%'," '()*+,!. 6$". 6%". 78-93:.$". +/;+/4.$". Florida の行列に対する CG 性能. 装ではスレッドブロック単位で同期を行っている．BCSR と我々が提案した分割フォーマットについて，比較実験. 6. 結論. を行った．実験には表 4 に記した行列を用いた．図 12 に. 世界のスーパーコンピュータで広く用いられている GPU. 結果を示す．CSR と BCSR の結果は彼らの論文のものを. などのメニーコアプロセッサを用いて，多くの科学技術計. 引用し，S-JDS の実験には同様に Fermi 世代の GPU であ. 算において性能に支配的なカーネルとなっている疎行列ベ. る Tesla M2070 を用いた．彼らの論文では GTX480 が用. クトル積計算の性能向上を図ることは極めて重要である. いられており，これらの比較（GTX480 vs. M2070）を行. といえる．しかしながら，GPU は一般的な CPU に比べ. うと，GTX480 はより多くの CUDA コアを持ち（480 vs.. キャッシュの容量が小さく，さらにランダムアクセスに対. 448），クロック数，ピーク性能も共に高く（1400MHz vs.. するハードウェア的サポートがないという欠点があるため，. 1150MHz，1344GFlops vs. 1030GFlops），さらに最も重要. 入力ベクトル要素へのランダムアクセスが発生する疎行列. であると考えられるメモリバンド幅も高い (177.4GB/sec. ベクトル積の性能が著しく低い．これに対し，我々は行列. vs. 148GB/sec)．このように GPU の性能に大きく開きが. を列方向で分割したフォーマットを新たに提案した．分割. あるにも関わらず，S-JDS フォーマットはより高い性能値. は入力ベクトルへも行われており，行列に対応する形で分. を示しており，Segmented 系フォーマットの有用性が確認. 割されている．これによりランダムアクセスによるキャッ. できる．. シュミス発生を大きく減らすことを可能とした．結果として疎行列ベクトル積カーネルにおいて，我々の提案する. 表 4. BCSR フォーマットの性能評価に用いた行列 N nnz category nnz/N. フォーマットは既存の GPU 向けフォーマットや NVIDIA. shipsec1. 140,874. 7,813,404. structural problem. 55.46. が提供しているライブラリのものからの性能向上を果たす. consph. 83,334. 6,010,480. 2D/3D problem. 72.13. ことに成功した．今後の課題として，我々の提案するフォーマットが他のメニーコアプロセッサ，例えば AMD Radeon GPU などにおいても有用であるかを確認する必要があると考えられ. CSR. BCSR. S-JDS. る．また，より詳細な性能モデルを構築し，自動最適化や. GFLOPS!. 20. フォーマットの自動選択につなげていく必要もある．謝辞. 15. 本研究の一部は科学研究費補助金基盤研究. (S)23220003 「１０億並列・エクサスケールスーパーコ. 10. ンピュータの耐故障性基盤」及び科学技術振興機構戦略的 5. 創造研究推進事業「EBD: 次世代の年ヨッタバイト処理に向けたエクストリームビッグデータの基盤技術」による。. 0 shipsec1. consph Matrix!. 参考文献図 12 Fermi 世代 GPU における，CSR，BCSR，SJDS の性能比較. ⓒ 2014 Information Processing Society of Japan. [1]. Jin, G., Endo, T. and Matsuoka, S.: A MultiLevel Optimization Method for Stencil Computation on the Domain that is Bigger than Memory Capacity of GPU, IEEE 27th International, Parallel and Dis-. 8.

(9) Vol.2014-HPC-144 No.5 2014/5/26. 情報処理学会研究報告 IPSJ SIG Technical Report. [2]. [3] [4] [5]. [6]. [7]. [8]. [9]. [10]. [11]. [12]. [13]. [14]. [15]. [16]. [17]. tributed Processing Symposium Workshops & PhD Forum (IPDPSW) 2013, IEEE, pp. 1080–1087 (2013). Rungsawang, A. and Manaskasemsak, B.: Fast pagerank computation on a GPU cluster, 20th Euromicro International Conference on Parallel, Distributed and Network-Based Processing (PDP 2012), IEEE, pp. 450– 456 (2012). Saad, Y.: Iterative methods for sparse linear systems, SIAM (2003). Davis, T.: The University of Florida Sparse Matrix Collection. Nishtala, R., Vuduc, R. W., Demmel, J. W. and Yelick, K. A.: When cache blocking of sparse matrix vector multiply works and why, Applicable Algebra in Engineering, Communication and Computing, Vol. 18, No. 3, pp. 297–311 (2007). Williams, S., Oliker, L., Vuduc, R., Shalf, J., Yelick, K. and Demmel, J.: Optimization of sparse matrix-vector multiplication on emerging multicore platforms, Parallel Computing, Vol. 35, No. 3, pp. 178–194 (2009). Lee, B. C., Vuduc, R. W., Demmel, J. W. and Yelick, K. A.: Performance models for evaluation and automatic tuning of symmetric sparse matrix-vector multiply, ICPP 2004: International Conference on Parallel Processing 2004, IEEE, pp. 169–176 (2004). Karakasis, V., Goumas, G. and Koziris, N.: Perfomance models for blocked sparse matrix-vector multiplication kernels, ICPP’09: International Conference on Parallel Processing 2009., IEEE, pp. 356–364 (2009). Monakov, A. and Avetisyan, A.: Implementing blocked sparse matrix-vector multiplication on NVIDIA GPUs, Embedded Computer Systems: Architectures, Modeling, and Simulation, Springer, pp. 289–297 (2009). Tang, W. T., Tan, W. J., Ray, R., Wong, Y. W., Chen, W., Kuo, S.-h., Goh, R. S. M., Turner, S. J. and Wong, W.-F.: Accelerating sparse matrix-vector multiplication on GPUs using bit-representation-optimized schemes, Proceedings of SC13: International Conference for High Performance Computing, Networking, Storage and Analysis, ACM, p. 26 (2013). Baskaran, M. M. and Bordawekar, R.: Optimizing sparse matrix-vector multiplication on GPUs using compiletime and run-time strategies, IBM Reserach Report, RC24704 (W0812-047) (2008). Cevahir, A., Nukada, A. and Matsuoka, S.: Fast conjugate gradients with multiple GPUs, Computational Science–ICCS 2009, Springer, pp. 893–903 (2009). Cevahir, A., Nukada, A. and Matsuoka, S.: High performance conjugate gradient solver on multi-GPU clusters using hypergraph partitioning, Computer ScienceResearch and Development, Vol. 25, No. 1-2, pp. 83–91 (2010). Monakov, A., Lokhmotov, A. and Avetisyan, A.: Automatically tuning sparse matrix-vector multiplication for GPU architectures, High Performance Embedded Architectures and Compilers, Springer, pp. 111–125 (2010). V´azquez, F., Fern´ andez, J.-J. and Garz´on, E. M.: A new approach for sparse matrix vector product on NVIDIA GPUs, Concurrency and Computation: Practice and Experience, Vol. 23, No. 8, pp. 815–826 (2011). Kreutzer, M., Hager, G., Wellein, G., Fehske, H. and Bishop, A. R.: A unified sparse matrix data format for modern processors with wide SIMD units, CoRR, Vol. abs/1307.6209 (2013). Bell, N. and Garland, M.: Implementing sparse matrix-. ⓒ 2014 Information Processing Society of Japan. [18] [19]. [20]. vector multiplication on throughput-oriented processors, Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis, ACM, p. 18 (2009). NVIDIA Corporation: cuSPARSE Library. Im, E.-J., Yelick, K. and Vuduc, R.: Sparsity: Optimization framework for sparse matrix kernels, International Journal of High Performance Computing Applications, Vol. 18, No. 1, pp. 135–158 (2004). Xu, W., Zhang, H., Jiao, S., Wang, D., Song, F. and Liu, Z.: Optimizing sparse matrix vector multiplication using cache blocking method on Fermi GPU, 13th ACIS International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel & Distributed Computing (SNPD) 2012, IEEE, pp. 231–235 (2012).. 9.

(10)