ハンドアウト toyo_classes
全文
図

![Figure 2.1: Web pages and their links. Adopted from [ Langville and Meyer , 2006 , p.32]](https://thumb-ap.123doks.com/thumbv2/123deta/5632121.2267/29.918.221.631.382.671/figure-web-pages-links-adopted-langville-meyer-p.webp)
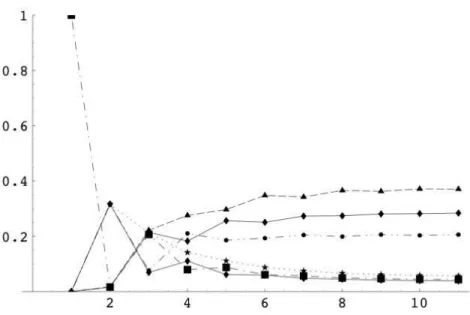
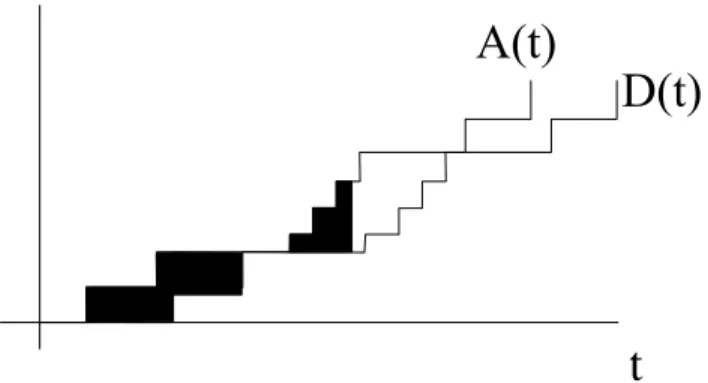
関連したドキュメント
Byeon, Existence of large positive solutions of some nonlinear elliptic equations on singu- larly perturbed domains, Comm.. Chabrowski, Variational methods for potential
It is suggested by our method that most of the quadratic algebras for all St¨ ackel equivalence classes of 3D second order quantum superintegrable systems on conformally flat
As application of our coarea inequality we answer this question in the case of real valued Lipschitz maps on the Heisenberg group (Theorem 3.11), considering the Q − 1
Then it follows immediately from a suitable version of “Hensel’s Lemma” [cf., e.g., the argument of [4], Lemma 2.1] that S may be obtained, as the notation suggests, as the m A
Definition An embeddable tiled surface is a tiled surface which is actually achieved as the graph of singular leaves of some embedded orientable surface with closed braid
We study the classical invariant theory of the B´ ezoutiant R(A, B) of a pair of binary forms A, B.. We also describe a ‘generic reduc- tion formula’ which recovers B from R(A, B)
These recent studies have been focused on stabilization of the lowest equal-order finite element pair P 1 − P 1 or Q 1 − Q 1 , the bilinear function pair using the pressure
Assuming the existence of an upper and a lower solution, we prove the existence of at least one bounded solution of a quasilinear parabolic sys- tems, with nonlinear second