Classes Yutaka Matsuno's Homepage 20160520

応用統計 第 ₄ 回

記述統計 _{(4) 2} 次元データの解析 ₍₂₎

応用情報工学科

准教授 松野 裕

matsuno.yutaka@nihon-u.ac.jp

2016 ^年 5 ^月 20 ^日

前回の講義と演習について

定量的データの定性的データの相関を見るための指標である、相関比の意味を考えてみる。

相関比₌

級間変動 級内変動₊級間変動

であり、取りうる値は₀から₁である。級内変動は、各定性的データのグループごとに、そのグループ内の平 均と、それぞれのデータの偏差平方和の和である。級間変動は、そのグループごとに、データ数と、そのグ ループの平均と全体の平均の偏差平方和の積の和である。

• 1となるのは、級内変動が０になるときである。すべての定性的データのグループに含まれるデータが 同一であるときである。すべてのデータが、定性的データとの対応によってはっきりと分けられるとき である。

• 0となるのは、級間変動が₀になるときである。各グループの平均が同一であるときである。すべての データが、定性的データとの対応に関係なく、定性的データによる相関はないと言える。

1 定性的データと定性的データの相関

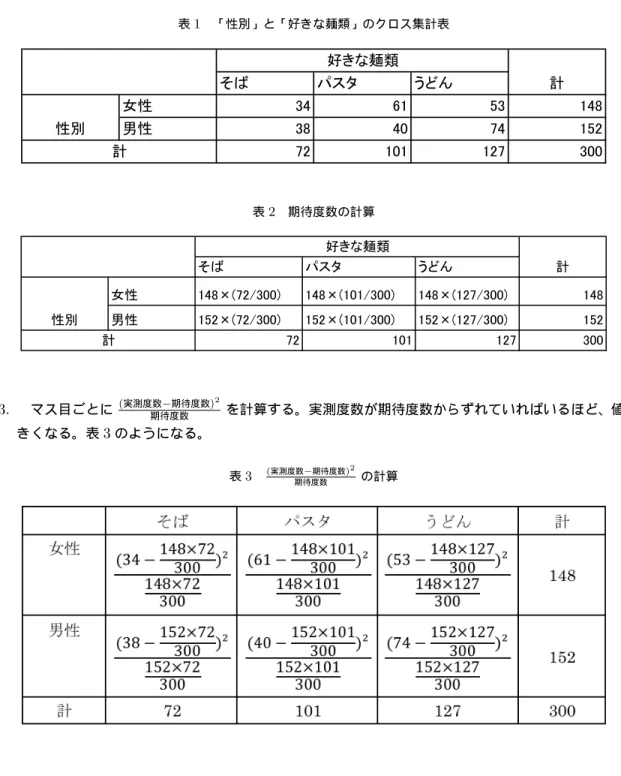
前回の続きで、定性的データと定性的データの相関について講義する。定性的データと定性的データの相関 は、クラメールの連関係数を指標として用いる。表₁に、例として「性別」と「好きな麺類」のクロス集計表 (２変数を掛けあわせた表のことをクロス集計表という₎を考える。例えば、男性で、うどんが好きと答えた人 は₇₄人、女性でパスタが好きと答えた人は₆₁人である。表₁において、34,61,53,38,40,74^{は実測度数と呼} ばれる。クラメールの連関係数の値は以下のステップで求められる。

1. クロス集計表を用意する。

2. ^表2に記した計算を行う。これらは期待度数と呼ばれる。期待度数は、もし「性別」と「好きな麺類」 が全く関係していない場合に期待される度数である。

1

表1 「性別」と「好きな麺類」のクロス集計表

!" #$% &'(

)* +, -. /+ .,0

1* +0 ,2 3, ./4

34 .2. .43 +22

*5

6789:

;

;

表2 期待度数の計算

!" #$% &'(

)* +,-./0123445 +,-./+4+23445 +,-./+1023445 +,- 6* +71./0123445 +71./+4+23445 +71./+1023445 +71

01 +4+ +10 344

*8 9

:;<=>

9

3. ^{マス目ごとに(実測度数}期待度数^{−期待度数)2}

を計算する。実測度数が期待度数からずれていればいるほど、値は大 きくなる。表₃のようになる。

表3 ^{(実測度数−期待度数)2}

期待度数

の計算

4. 前で計算した値をすべて足す。これをピアソンのカイ二乗統計量と呼び、_χ²₀で表す。

χ²₀=^{(34 −}

148×72 300 ⁾² 148×72

300

+^{(61 −}

148×101 300 ⁾² 148×101

300

+^{(53 −}

148×127 300 ⁾² 148×127

300

+^{(38 −}

152×72 300 ⁾² 152×72

300

+^{(40 −}

152×101 300 ⁾² 152×101

300

+^{(74 −}

152×127 300 ⁾² 152×127

300

= 8.0091

2

5. クラメールの連関係数は

√

χ²₀

全データの個数_{× (min{}クロス集計表の行数_,クロス集計表の列数_{} − 1)}

である_{(min(a, b)}は_{a, b}のうち、小さい方を返す関数である。₎この場合以下のように計算される。

√ 8.0091

300 × (min{2, 3} − 1) ⁼

√ 8.0091 300 × (2 − 1) ⁼

√ 8.0091

300 ^{= 0.1634}

クラメールの連関係数は₀から₁の値をとり、₁に近いほど相関があると言える。ただし「クラメールの連関 係数が_XX以上ならば、２変数は強く関連している」との統計学的な基準はない。一応の目安として、_1.0-0.8, 0.8-0.5, 0.5-0.25, 0.25以下の４つの範囲に分け、最後の_0.25以下の場合は「関連していない」ということが 多い。

2 ^{単回帰分析}

二変数_{x, y}を考える。_xが年齢、_yが血圧とすると、_xはある程度_yを決定する。このように₂変数_xと_y の間に、一方_xが他方_yを左右ないしは決定する関係があるとき、_xは独立変数(independent variable)^、 y^{は従属変数}(dependent variable)という（あるいは説明変数、被説明変数ということもある）。２変数の 間のこのような関係を分析することを単回帰分析という。一方、ある変数が複数の他の変数によって決定され る関係を分析することを重回帰分析という。実用の場では、単回帰分析を用いることが大半である。回帰分析 を行う対象となるデータは、すべて定量的データである。

回帰関係を調べるために適切な直線を求めよう。最小₂乗法による。求める直線を回帰式と呼び、 y = bx + a

とする。ここで_bを回帰係数_{, a}を切片という。各点_{(xi, yi)}と_{y = bx + a}と距離の和が最小になるように a, b^{を求める。そのために}2^乗和(sum of squares):

L =

n

∑

i=1

{yi− (bxi+ a)}²

を最小にする_{a, b}を求める。_Lは_{a, b}の₂変数関数の₂次式だから、最小を求めるために_{a, b}でそれぞれ偏 微分して₀とおくと、結果として、

na + (^∑xi)b =^∑yi

(^∑xi)a + (^∑xi²)b =^∑xiyi

となる。これを正規方程式(normal equation)ということがある。これを_{a, b}について解くと、 b = ^{∑ xiyi− nxy}

∑ xi²− nx^{2 ,} a = y − bx

となる_{(x =∑ xi/n, y =∑ yi/n)}。

3

回帰と相関の考え方には、つながりがある。_bを変形すると、以下になる。 b = ^{∑(xi− x)(yi− y)}

∑(xi− x)² ここで

∑(xi− x)(yi− y) =^∑xiyi− nxy,

∑(xi− x)²=^∑x²_i − nx²

を用いた。

単相関係数_rxyと書くと

rxy = ^{∑(xi− x)(yi− y)}

√∑(xi− x)²√∑(yi− y)^{2 =}

∑(xi−x)(yi−y) n

√∑ (xi−x)²

n

√∑ (yi−y)²

n

= ^cxy sxsy

と比較する。ここで、_{sx, sy}は_{x1, . . . , xn}, {y1, . . . , yn}^{の標準偏差であり、}cxyは、それらの共分散と呼ば れる。

b = rxy· ^sy sx

= ^cxy sxsy

· ^sy sx

= ^cxy s²_x が得られる。これから、切片_{a = y − bx}も求められる。

問 上式を示せ。

また、_rxy² を決定係数(coefficient of determination)^{という。目安として、}r²_xy^が0.5(rxy^が0.7^程度) より大きい場合は、その回帰式は信頼できるが、あくまで目安である。

参考文献

今回の内容は、「マンガで分かる統計学、高橋信著、オーム社」、「統計学入門、東京大学教養学部統計学教 室、東京大学出版会」、「それ、根拠あるの？と言わせないデータ・統計分析が出来る本、柏木吉基、日本実業 出版社」を参考にした。

4