Classes Yutaka Matsuno's Homepage 20160617

応用統計 第 ₉ 回

推測統計 _(1): 推測統計の基本的な考え方

応用情報工学科

准教授 松野 裕

2016 _年 6 _月 17 _日

1 推測統計の基本的な考え方

推測統計とは、日本人全体などの母集団(population)から、実際に調査対象となる母集団の一部を標本

sample^{として抽出}samplingし、標本を解析することにより母集団について推測することである。推測す

る内容は、母集団の平均_µ、分散_σ

2

などである。これらを総称して母数 _parameterという。母集団の分布 は、正規分布であると仮定することが多い。自然界、社会における多くの現象が、正規分布に従うことが知ら れている。

母集団から標本を取り出す方法は、母集団の数が_N（_{N = ∞}であるとすることが多い）、標本数を_nとす ると、N_Cn個の標本の取り出し方がある。標本の取り出し方は、母集団からの各要素が標本として取り出さ れる確率を等しく_n/Nとする、単純ランダム・サンプリングを考えるのが普通である。取り出し方によって 標本は異なるので、標本に対して、確率的取り扱いが必要である。母集団の確率分布を_{f (x)}とする。標本は 母集団からランダムに選ぶのであるから、それぞれの標本は、この母集団分布に従う確率変数であると考えら れる_:

標本_{X1, X2}, . . . , X^{nは、同一の母集団分布}f (x)^に従うn個の独立な確率変数である。

このとき、_{f (x)}は問題に応じて、連続型でも離散型でもよい。例として、日本人（有限集団だが、無限集団と 考えて良い）の身長という母集団と標本の例を図₁に示す。図₁の標本は、一例に過ぎず、サンプリングの度

図₁ 日本人の（身長）という母集団と標本

1

に変わりうる。その分布は、母集団の確率密度関数_{f (x)}に従う。

1.1 中心極限定理

推測統計の基本原理である、中心極限定理を示す。おおまかに言えば母集団分布が何であっても、標本の和 X1+ · · · + X^{nの確率分布の形は、n}が大きい時は、大体、正規分布と考えてよいということである。

1.2 母数と統計量

母集団の特徴を表すパラメータとして、最も使われるのは母平均 population mean µ^と母分散 popu- lation variance σ²である。これは主に以下の理由による。

• µ^とσ2は分布の位置とばらつきを規定すること。

• 母集団分布が正規分布の場合、この二つの母数_{µ, σ}

2

で母集団分布の特性を完全に表現できること。

標本において、母平均、母分散に対応するものは、標本平均_X、不偏標本分散_s

2

である_: X = ^X1+ · · · + Xⁿ

n s²= ¹

n − 1^{{(X1− X)}

2+ · · · + (Xⁿ− X)²}

Xは、その期待値と分散を取ると（分散を求める時、標本の独立性を用いている）、 E(X) = E(^X1+ · · · + Xⁿ

n ^{) =}

1

n^(E(X1) + · · · + E(X^{n)) =} _n¹ · nµ = µ V (X) = V (^X1+ · · · + Xⁿ

n ^{) =}

1

n^{2(V (X1}) + · · · + V (X^{n)) =} _n¹2 · nσ^{2= σ}

2

n つまり、_Xは_µを偏りなく、平均的に推定する。さらに、分散が

σ2

n ^だから、n → ∞^{のとき、分散は0に近} づき、_{X → µ}のように定数_µ(母平均₎に集中、確率収束していく。

不偏標本分散_s²を、いままで用いてきた分散_s² s²= ¹

n^{{(X1− X)}

2+ · · · + (Xⁿ− X)²}

の代わりに用いるのは、_s²の期待値_E(s²₎が

E(s²) = σ²

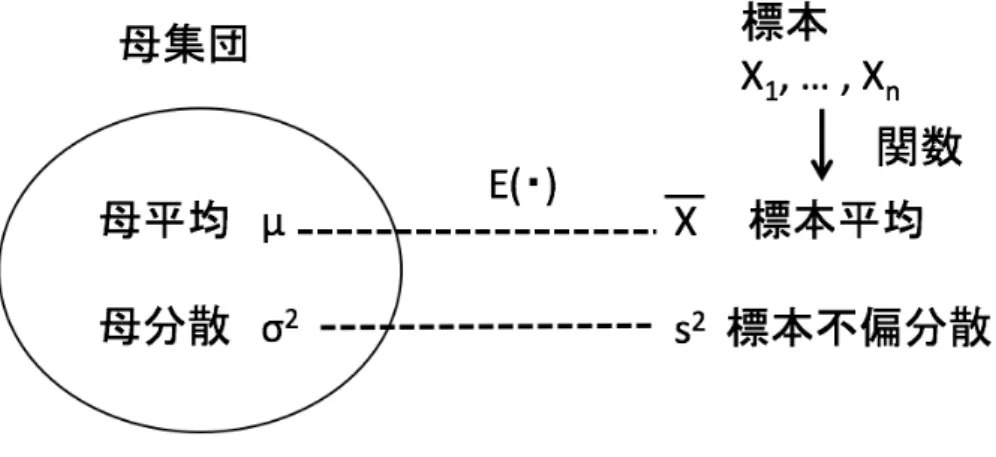
を満たすからである。つまり、_s²は、母分散_σ²を偏りなく_(unbiased)推定できる。_µと_σ²、_X と_s²の関 係を図示すると、図₂になる。

1.3 _{正規分布からの標本}

本講義では、正規母集団を主な対象とする。確率変数_X が正規分布に従う時、確率密度関数は以下で表さ れる。

f (x) = √¹ 2πσ^exp{

−(x − µ)²

2σ² }, − ∞ < x < ∞

2

図₂ 母集団と標本の関係

N (µ, σ²)で表す。期待値、分散は以下である。

E(X) = µ, V (X) = σ²

標本_X1, . . . , Xⁿは母集団分布と同一の分布に従う独立な確率変数であるから、各々独立で_{N (µ, σ}

2)^に従 う。正規分布の性質を使うと標本平均_{X =}

X1+···+Xⁿ

n ^は、N (µ,^σn²)^{に従う。この結果は、}n^{が十分に大きい} 時、中心極限定理を使ったときと同じである。母集団を正規分布であると仮定できないときは、_nが十分に大 きくないと、標本平均が正規分布に従うとは言えない。

標本平均_Xを標準化した

Z = ^{X − µ}σ

√n

は標準正規分布_{N (0, 1)}に従う。_X の標準偏差は_σ/

√n^である。

これを用いて母平均_µを推定してみよう。正規分布表を用いて−1.96 ≤ Z ≤ 1.96^{となる確率を求める。} P (−1.96 ≤ Z ≤ 1.96) = Φ(1.96) − Φ(−1.96) = 2 · Φ(1.96) − 1 = 2 · 0.975 − 1 = 0.95

つまり、−1.96 ≤ Z ≤ 1.96^{である確率は95%}であるといえる。つまり、

−1.96 ≤ ^{X − µσ}

√n ^{≤ 1.96}

である確率は_95%である。更に式変形をすると、 X − 1.96√^σ

n ≤ µ ≤ X + 1.96√^σ n

である確率は_95%である。これを母平均の_95%信頼区間という。範囲として、 [X_{− 1.96√}^σ

n^{, X + 1.96}

√σ_n^]

と書く。

X, σ, nは与えられているとすると、_95%の正しい確率で、母平均_µを推定できることになる。この考え方

が推測統計の基本である。

3

参考文献

今回の内容は、「統計学入門、東京大学教養学部統計学教室編、東京大学出版会」、「入門統計学−検定から 多変量解析・実験計画法まで−、栗原伸一、オーム社」を参考にした。

4