Lecture 12: Dynamic Games with Incomplete
Information
Advanced Microeconomics II
Yosuke YASUDA
National Graduate Institute for Policy Studies
January 16, 2014
1 / 11
Dynamic Games with Imperfect Information
In dynamic games of incomplete information, there is no subgame other than the entire game. Therefore, SPNE necessarily coincides with NE and hence cannot help excluding implausible equilibria.
◮ Even though there is no asymmetric information at the beginning, SPNE sometime predicts unreasonable outcomes. Entry Game An incumbent faces the possibility of entry by a challenger. The challenger has three choices:
1. It may stay out (O),
2. prepare itself for combat and enter (“Ready” = R), 3. or enter without making preparations (“Unready” = U ). Preparation is costly but reduces the loss from a fight. The incumbent may either fight (F ) or accommodate (A) entry. Depending on the payoffs, we consider two cases.
2 / 11
Case 1
C I A F
R 3, 3 1, 1 U 4, 3 0, 2 O 2, 4 2, 4
There are two Nash equilibria (also SPNE): (U, A), (O, F ).
◮ The second equilibrium seems unreasonable since A strongly dominates F once the challenger decides to enter (R or U ) the market.
◮ That is, given that the incumbent’s information set is reached, choosing A is clearly optimal irrespective of her belief over nodes. → Choosing F looks non-credible.
◮ SPNE cannot eliminate this since there is no proper subgame. Weak perfect Bayesian equilibrium (explain in detail later) is enough to exclude (O, F ) in this case.
3 / 11
Case 2
C I A F
R 4, 2 1, 1
U 3, 2 0, 3
O 2, 4 2, 4
There are two Nash equilibria (also SPNE): (R, A), (O, F ).
◮ Again, the second equilibrium seems unreasonable since R strongly dominates U and A is best reply against R.
◮ That is, given that the incumbent’s information set is reached, it is reasonable for the incumbent to expect that the
challenger has chosen R, not U .
◮ Choosing F is inconsistent with this expectation.
Since (O, F ) is still a weak perfect Bayesian equilibrium, we have to strengthen the equilibrium concept to perfect Bayesian
equilibrium in order to eliminate this unreasonable equilibrium.
4 / 11
Perfect Bayesian Equilibrium (1)
We introduce the new solution concepts, perfect Bayesian equilibrium (PBE) and its weak version, which strengthen the requirements of SPNE by explicitly analyzing the players’ beliefs.
(1) At each information set, the player with the move must possess a belief µ(·) about which node x in the information set h(x) has been reached by the play of the game.
◮ That is, a belief µ(h) is a conditional probability distribution over the nodes in the information set h.
◮ For a singleton information set, i.e., x = h(x), the player’s belief puts probability one on the single decision node. (2) Given their beliefs, the players’ strategies must be
sequentially rational. That is, at each information set, the action taken by the player must be optimal given
(i) the player’s belief at that information set and (ii) the other players’ subsequent strategies.
5 / 11
Perfect Bayesian Equilibrium (2)
(3) At information sets on the equilibrium path, beliefs are determined by
(i) Bayes’ rule and
(ii) the players’ equilibrium strategies.
(4) At information sets off the equilibrium path, beliefs are determined by Bayes’ rule and the players’ equilibrium strategies whenever possible.
Def For a given equilibrium in a given extensive form game, an information set is called
◮ on the equilibrium path if it will be reached with positive probability if the game is played according to the equilibrium strategies, and
◮ off the equilibrium path if it is certain not to be reached by the equilibrium strategies.
6 / 11
Perfect Bayesian Equilibrium (3)
Def Perfect Bayesian equilibrium (PBE) consists of strategies (complete plan of actions for all players) and beliefs (defined over every information set) satisfying (1) through (4):
◮ Each player’s strategy specifies optimal actions given her beliefs and the strategies of the other players, and
◮ The beliefs are consistent with Bayes’ rule wherever possible. If (4) is not required, the equilibrium concept is called weak perfect Bayesian equilibrium (weak PBE).
✞
✝
☎
Rm In essence, the PBE is a solution concept that incorporates✆ sequential rationality and consistency of beliefs.
The crucial new feature of PBE due to Kreps and Wilson (1982):
◮ Equilibrium no longer consists of just a strategy for each player but now also includes a belief for each player at each information set at which the player has the move.
7 / 11
Signaling Game (1)
A signaling game is a dynamic game of incomplete information involving two players: a Sender (S) and a Receiver (R).
The timing of the game is as follows:
1. Nature draws a type ti for the Sender from a set of feasible types T = {t1, ..., tI} according to a probability distribution p(ti), where p(ti) > 0 for every i and p(t1) + · · · + p(tn) = 1. 2. Sender observes ti and then chooses a message mj from a set
of feasible messages M = {m1, ..., mJ}.
3. Receiver observes mj (but not ti) and then choose an action ak from a set of feasible actions A = {a1, ..., aK}.
4. Payoffs are given by uS(ti, mj, ak) and uR(ti, mj, ak).
8 / 11
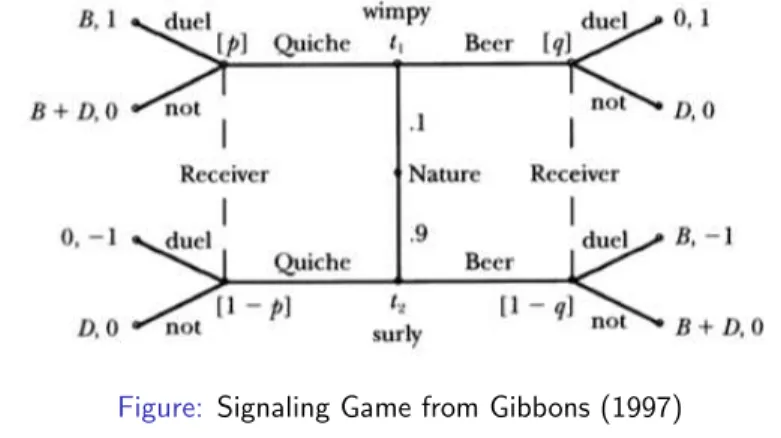
Signaling Game (2)
Figure: Signaling Game from Gibbons (1997)
Def Sender’s strategies are called (i) pooling when all types choose the same action, (ii) separating when each type chooses different actions, (iii) semi-separating when several actions are chosen but some action is chosen by more than one type.
Illustration Application 4.2.A (Gibbons, pp.183-190)
9 / 11
Signaling Game (3)
B > D The Sender’s strategy (Quiche if w, Beer if s) and the Receiver’s strategy (duel after Q, not after B), together with the beliefs p = 1 and q = 0 satisfy (2)-(4) and so constitute a PBE.
◮ The separating equilibrium derived above is the unique PBE of the Beer and Quiche signaling game when B > D. B < D There is no separating equilibrium. But there are following two pooling equilibria.
1. (Beer, Beer) and (duel, not), with p = 1 and q = 0.1.
◮ In fact, any belief p ≥ 0.5 would work as well.
2. (Quiche, Quiche) and (not, duel), with p = 0.1 and q = 1.
◮ In fact, any belief q ≥ 0.5 would work as well.
The first equilibrium makes sense (just as the separating one above made sense when B > D), but the second one may not.
◮ Cho and Kreps (1987) argue that the Receiver’s belief in this equilibrium is “counterintuitive”. Their intuitive criterion
refines PBE, which indeed rules out this pooling equilibrium. 10 / 11
Sequential Equilibrium by Kreps and Wilson (1982)
Def (σ, µ) is sequentially rational if, for any information set h and alternative strategy σi(h)′ ,
ui(h)(σ | h, µ(h)) ≥ ui(h)(σi(h)′ , σ−i(h) | h, µ(h)) where i(h) is the player who has the move at h.
Def (σ, µ) is consistent if for some sequence (σn, µn), (σ, µ) = lim
n→+∞(σ n, µn)
where σn is completely mixed (behavioral) strategy, i.e., σi(ai | h) > 0 for all h and ai∈ A(h).
◮ Under σn, every information set is reached with positive probability, so Bayes’ rule completely pins down beliefs µn. Def A sequential equilibrium is a combination of strategies and beliefs that satisfies sequential rationality and consistency.
11 / 11