ランダムな局所的対戦構造をもつ適応プロセス
がゲームの均衡選択に与える影響
宮下 春樹・福住 多一
1
イントロダクション
本研究ノートは,進化ゲーム理論におけるプレイヤーどうしの対戦構造の違
いが均衡選択におよぼす影響について考察する.通例,各プレイヤーは集団内
のあらゆるプレイヤーと,ランダムに対戦すると想定される.本研究ノートは,
各プレイヤーの対戦相手が,ランダムに選ばれた集団の一部である場合の分析
を進める.先行研究としてHilbe (2011)はプレイヤーどうしの対戦が,無限母 集団からランダムに選ばれた有限集団という局所的構造をもつ連続時間のレプ
リケータ-動学を定式化している.本研究ノートは,次のような適応プロセス
が均衡選択に与える影響を検討する.毎期,有限母集団から有限人数のランダ
ムな対戦相手が選ばれる局所対戦構造を想定する.その対戦相手の戦略分布に
動学を鹿狩りゲームと制裁が加わった囚人のジレンマゲームに適用し,その場
合のプレイヤー集団の安定状態が示す特徴を数値例で検討する.
2
モデル
我々はHilbe (2010)と異なり,有限の母集団から一部の対戦プレイヤーが
ピックアップされ,最適反応によって母集団の状態が変化していく適応プロセ
スを定式化する.M = {1,2, ..., m}をプレイヤー母集団とする.このプレイ ヤー集団から毎期t= 0,1,2, ...に,その部分集合N ⊆Mがランダムにピック アップされる.ここでN ={1,2, ..., n},(n≤m)である.N内でプレイヤーは ランダムに2人の組を形成する.その各組は次のゲームG(S, u)をプレイする.
S={s1, s2, ..., sk}を各プレイヤーの純粋戦略の集合とする.u(si, sj)∈Rを戦 略siをとるプレイヤーがsjをとるプレイヤーとのプレイから得る利得とする.
2.1
適応プロセス
各t期のプレイヤー母集団の状態をベクトルm(t) = (m1(t), m2(t), ..., mk(t)) で表す.ただし,
k
∑
i=1
mi=mであり,各miは戦略siにコミットメントしている プレイヤーの人口である.また各t期においてMからNがランダムにピックアッ
動学を鹿狩りゲームと制裁が加わった囚人のジレンマゲームに適用し,その場
合のプレイヤー集団の安定状態が示す特徴を数値例で検討する.
モデル
我々は と異なり,有限の母集団から一部の対戦プレイヤーが
ピックアップされ,最適反応によって母集団の状態が変化していく適応プロセ
スを定式化する. をプレイヤー母集団とする.このプレイ
ヤー集団から毎期 に,その部分集合 がランダムにピック
アップされる.ここで である. 内でプレイヤーは
ランダムに 人の組を形成する.その各組は次のゲーム をプレイする.
を各プレイヤーの純粋戦略の集合とする. を戦
略 をとるプレイヤーが をとるプレイヤーとのプレイから得る利得とする.
適応プロセス
各 期のプレイヤー母集団の状態をベクトル
で表す.ただし, であり,各 は戦略 にコミットメントしている
プレイヤーの人口である.また各 期において から がランダムにピックアッ
プされるとし, における 期の状態は次のベクトル
127 動学を鹿狩りゲームと制裁が加わった囚人のジレンマゲームに適用し,その場
合のプレイヤー集団の安定状態が示す特徴を数値例で検討する.
モデル
我々は と異なり,有限の母集団から一部の対戦プレイヤーが
ピックアップされ,最適反応によって母集団の状態が変化していく適応プロセ
スを定式化する. をプレイヤー母集団とする.このプレイ
ヤー集団から毎期 に,その部分集合 がランダムにピック
アップされる.ここで である. 内でプレイヤーは
ランダムに 人の組を形成する.その各組は次のゲーム をプレイする.
を各プレイヤーの純粋戦略の集合とする. を戦
略 をとるプレイヤーが をとるプレイヤーとのプレイから得る利得とする.
適応プロセス
各 期のプレイヤー母集団の状態をベクトル
で表す.ただし, であり,各 は戦略 にコミットメントしている
プレイヤーの人口である.また各 期において から がランダムにピックアッ
プされるとし, における 期の状態は次のベクトル
で表現される.ただし は の中で にコミットメントしているプレイヤー
の人口である.各期の においてランダムにプレイヤーが 人ピックアップさ
れ,実現している に対して 期の期首に最適反応することにより,そ
の戦略を変更すると仮定する.
2.2
状態の推移確率
推移確率Pr(m(t+1)|m(t))を求める.m(t)からn(t) = (n1(t), n2(t), ..., nk(t)) をピックアップする確率は超幾何分布(hyper geometric distribution)に従う.つ まり,この確率は
m1Cn1· · ·mkCnk
MCN
(1)
である.戦略siをとっているプレイヤーがピックアップされる確率はni (t) n(t)であ
る.このプレイヤーが戦略sjをとる場合の期待利得は,
Eui(sj|n(t)) =nni((tt)−1)−1ui(si, si) +
∑
j̸=i nj(t)
n(t)−1ui(si, sj).
t+1期に戦略iのプレイヤーが最適反応に基づいてコミットメントする戦略はs∗j∈
arg max
sj∈S
Eui(sj|n(t))である.ここでBRi(n(t)) : = arg max sj∈S
Eui(sj|n(t))と書く. 各s∗
jをとる確率は|BR1(n(t))|とする.siにコミットメントしているプレイヤーがピ ックアップされ,BR(n(t)) ={s∗j}であるとき,mi(t)は一人減り,mj(t)は一人増 える.各戦略siにコミットメントしているプレイヤーをそれぞれピックアップする で表現される.ただしniはNの中でsiにコミットメントしているプレイヤー
の人口である.各期のNにおいてランダムにプレイヤーが1人ピックアップさ れ,実現しているn(t)に対してt+ 1期の期首に最適反応することにより,そ の戦略を変更すると仮定する.
状態の推移確率
推移確率 を求める. から
をピックアップする確率は超幾何分布 に従う.つ
まり,この確率は
である.戦略 をとっているプレイヤーがピックアップされる確率は であ
る.このプレイヤーが戦略 をとる場合の期待利得は,
期に戦略 のプレイヤーが最適反応に基づいてコミットメントする戦略は
である.ここで と書く.
各 をとる確率は とする. にコミットメントしているプレイヤーがピ
ックアップされ, であるとき, は一人減り, は一人増
確率は,ni(t)
n(t)であるから,m(t+1) = (m1(t), ..., mi(t)−1, ..., mj(t)+1, ..., mk(t)) である場合,
pr(m(t+ 1)|m(t)) = k
∑
i=1
m1Cn1· · ·mkCnk MCN
×ni(t) n(t) ×
1
|BR(n(t))| (2)
である.
3
具体的なゲームへの適用
本章では我々の定式化した適応プロセスでパラメーター値を特定化したもの
を,鹿狩りゲームと制裁戦略を加えた囚人のジレンマゲームに適用し,母集団
の状態の安定性を分析する.
3.1
鹿狩りゲーム
プレイヤーの純粋戦略の集合をS={S, H}とし,式(3)の利得行列Π1をも
つ鹿狩りゲームを考える:
Π1=
S H
S 5 0 H 4 2
確率は, であるから,
である場合,
である.
具体的なゲームへの適用
本章では我々の定式化した適応プロセスでパラメーター値を特定化したもの
を,鹿狩りゲームと制裁戦略を加えた囚人のジレンマゲームに適用し,母集団
の状態の安定性を分析する.
鹿狩りゲーム
プレイヤーの純粋戦略の集合を とし,式 の利得行列 をも
つ鹿狩りゲームを考える
129
確率は, であるから,
である場合,
である.
具体的なゲームへの適用
本章では我々の定式化した適応プロセスでパラメーター値を特定化したもの
を,鹿狩りゲームと制裁戦略を加えた囚人のジレンマゲームに適用し,母集団
の状態の安定性を分析する.
鹿狩りゲーム
プレイヤーの純粋戦略の集合を とし,式 の利得行列 をも
つ鹿狩りゲームを考える
とする.このゲームをプレイするプレイヤーの対戦人数が の
場合における状態推移図を図 ,図 にそれぞれ示す.図 ,図 内の各状態か
ら次の状態へ正の確率 で推移する場合,そのパスを矢印で示
し,矢印がない状態への推移確率は である. 図 ,図 において,全プレイ
ヤーが をとる状態 と全プレイヤーが をとる状態 に注目しよ
う. のとき,状態 から へ到達するには,集団状態の突然変
異が 回だけ生じ, から へと置き換えられればよい.一方,
から へ到達するのに必要な突然変異数は 回である. の場合には,
から へ到達するための突然変異数は 回であり, から
へ到達するのには 回必要である.つまり戦略 はピックアップされる
の人数が少ないとき,少数の突然変異によって に置き換わるが,人数が増え
るにつれて置き換わりにくくなる.この結果は,最適反応動学を用いて集団全
体とのマッチングを想定したときの長期確率安定状態が となるよく知られた
結果 と類似している.
3.2
制裁戦略を加えた囚人のジレンマゲーム
Weibull and and Salomonsson (2006)に従い,プレイヤーが非協力者を制裁 する戦略をもつ囚人のジレンマゲームを導入する.各プレイヤーの戦略は協力
する(CN),協力しない(D),そして制裁をする(CP)である.CPはCNとの
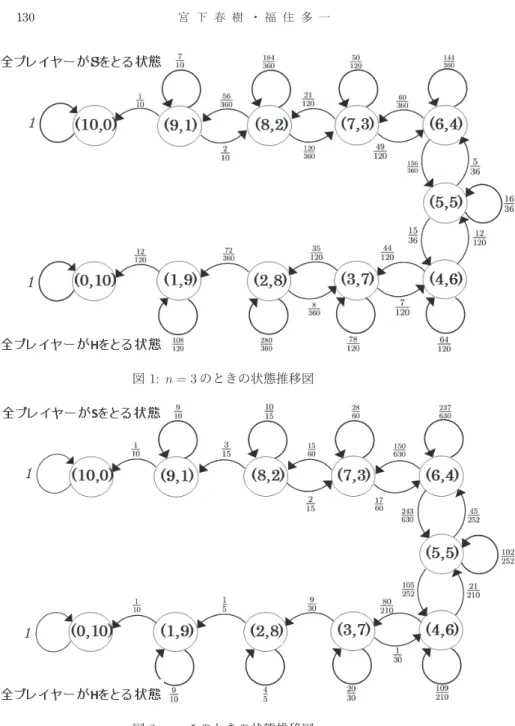
m= 10とする.このゲームをプレイするプレイヤーの対戦人数がn= 3,5の 場合における状態推移図を図1,図2にそれぞれ示す.図1,図2内の各状態か ら次の状態へ正の確率pr(m(t+ 1)|m(t))で推移する場合,そのパスを矢印で示 し,矢印がない状態への推移確率は0である. 図1,図2において,全プレイ ヤーがSをとる状態 (10,0)と全プレイヤーがHをとる状態 (0,10)に注目しよ う.n= 3のとき,状態(10,0)から(0,10)へ到達するには,集団状態の突然変 異が1回だけ生じ,(10,0)から(9,1)へと置き換えられればよい.一方,(0,10)
から(10,0)へ到達するのに必要な突然変異数は2回である.n= 5の場合には,
(10,0)から(0,10)へ到達するための突然変異数は2回であり,(0,10)から(10,0) へ到達するのには3回必要である.つまり戦略SはピックアップされるN ⊆M
の人数が少ないとき,少数の突然変異によってHに置き換わるが,人数が増え るにつれて置き換わりにくくなる.この結果は,最適反応動学を用いて集団全
体とのマッチングを想定したときの長期確率安定状態がHとなるよく知られた 結果(Kandori, Mailath and Rob (1993), Young (1993) )と類似している.
制裁戦略を加えた囚人のジレンマゲーム
に従い,プレイヤーが非協力者を制裁
する戦略をもつ囚人のジレンマゲームを導入する.各プレイヤーの戦略は協力
図1: n= 3のときの状態推移図
図 のときの状態推移図
図 のときの状態推移図
131
対戦では をとり, との対戦においては のコストを負担することで相
手の利得を だけ減少させる. と の対戦において, を選択するプ
レイヤーは の利得を得る.この対戦において, を選択するプレイヤー
は の利得を得る. 対Dの対戦において をとるプレイヤーの利得は
であり, をとるプレイヤーは の利得を得る.このゲーム
の利得行列は で与えられる.
Π2=
C N C P D
C N 2 2 a
C P 2 2 a −c
D b b −d 1
. (4)
以下の分析ではa =1
2,b = 3とし,制裁コストが低く(c = 1
4),被制裁コストが
高い場合(d = 14
5)に限定する.
m = 8, n= 3とする.すると第t期における集団の状態は(8,0,0), (7,1,0),...,(0,0,8)
であり,合計45個存在する.式(2)を用いることにより,45×45推移確率行列
P= [p] =1,...,45を得る.各成分p は式(2)によって求められる.この推移確
率行列を表1に示してある.
表1より,すべてのプレイヤーがCPをとる状態(0,8,0)は,確率1
2で(1,7,0)
に推移する.また(1,7,0)は確率3
8で(2,6,0)へ推移する.このような推移確率行
対戦ではCNをとり,Dとの対戦においてはc >0のコストを負担することで相
手の利得をd >0だけ減少させる.CNとDの対戦において,CNを選択するプ
レイヤーはa <1の利得を得る.この対戦において,Dを選択するプレイヤー
はb >3の利得を得る.CP対Dの対戦においてCPをとるプレイヤーの利得は
a−c <1であり,Dをとるプレイヤーはb−d <2の利得を得る.このゲーム
の利得行列はΠ2で与えられる.
以下の分析では , とし,制裁コストが低く ,被制裁コストが
高い場合 に限定する.
とする.すると第 期における集団の状態は
であり,合計 個存在する.式 を用いることにより, 推移確率行列
を得る.各成分 は式 によって求められる.この推移確
率行列を表 に示してある.
表 より,すべてのプレイヤーが をとる状態 は,確率 で
列に従っていくことで,(0,8,0)は10ステップで(0,0,8)へ到達する.すなわち,
集団の状態は微小な確率でCNをとるプレイヤーが増加し,CNを選択するプ
レイヤーの人数の多い状態へと推移する.CNをとるプレイヤーが増加するの
に伴い,各プレイヤーにはDを選択するインセンティブが働く.するとDをと
るプレイヤーの人数の多い状態へと到達する.つまり我々の定式化した適応プ
ロセスにおいては制裁コストが低く,被制裁コストが高い場合であっても,長
期的には全員がDを選択する状態で集団が落ち着くのである.
4
ディスカッション
Hilbe (2011)は,無限集団内で局所的にゲームがプレイされるときの連続時
間のレプリケーター動学を導入している.この集団からn≥2人のプレイヤー
をピックアップする.プレイヤーは,この集団内でランダムにゲームをプレイ
する.このときのレプリケーター動学を局所的レプリケーター動学(local
repli-cator dynamics)と呼ぶ.Π2ゲームの混合戦略空間を∆ ={(x CN, xCP, xD) ∈
R3+|xCN+xCP+xD= 1}と書き,第i成分が1であり,残りが0であるベクト ルをei= (0, ...,0,1,0, ...,0)と書く.
列に従っていくことで, は ステップで へ到達する.すなわち,
集団の状態は微小な確率で をとるプレイヤーが増加し, を選択するプ
レイヤーの人数の多い状態へと推移する. をとるプレイヤーが増加するの
に伴い,各プレイヤーには を選択するインセンティブが働く.すると をと
るプレイヤーの人数の多い状態へと到達する.つまり我々の定式化した適応プ
ロセスにおいては制裁コストが低く,被制裁コストが高い場合であっても,長
期的には全員が を選択する状態で集団が落ち着くのである.
ディスカッション
は,無限集団内で局所的にゲームがプレイされるときの連続時
間のレプリケーター動学を導入している.この集団から 人のプレイヤー
をピックアップする.プレイヤーは,この集団内でランダムにゲームをプレイ
する.このときのレプリケーター動学を局所的レプリケーター動学
と呼ぶ. ゲームの混合戦略空間を
と書き,第 成分が であり,残りが であるベクト
ルを と書く.
定理 ゲームの利得行列を とし, の転置行列を
133
列に従っていくことで, は ステップで へ到達する.すなわち,
集団の状態は微小な確率で をとるプレイヤーが増加し, を選択するプ
レイヤーの人数の多い状態へと推移する. をとるプレイヤーが増加するの
に伴い,各プレイヤーには を選択するインセンティブが働く.すると をと
るプレイヤーの人数の多い状態へと到達する.つまり我々の定式化した適応プ
ロセスにおいては制裁コストが低く,被制裁コストが高い場合であっても,長
期的には全員が を選択する状態で集団が落ち着くのである.
ディスカッション
は,無限集団内で局所的にゲームがプレイされるときの連続時
間のレプリケーター動学を導入している.この集団から 人のプレイヤー
をピックアップする.プレイヤーは,この集団内でランダムにゲームをプレイ
する.このときのレプリケーター動学を局所的レプリケーター動学
と呼ぶ. ゲームの混合戦略空間を
と書き,第 成分が であり,残りが であるベクト
ルを と書く.
定理 ゲームの利得行列を とし, の転置行列を
と書く.局所的レプリケーター動学は
˙
xixi·[ei·Ax˜ −x·Ax]˜ (5)
によって与えられる.ただし の上付き文字のドットは時間微分 を表し,
である.
とする. ゲームの 内における局所的レプリケーター動学の軌道を
位相図として図 に表す. 図中の黒丸 ● はその点が安定的な定常状態である
ことを表し,白丸 ○ は不安定であることを表す. を と をとる
プレイヤーが混在する状態において をとるプレイヤーの割合とする.辺
上に と が混在する安定的な均衡の集合
が存在する.
先に定式化した式 の適応プロセスにおいては, ゲームでは をとるプ
レイヤーのみからなる均衡は安定性をもたず,集団の全プレイヤーが を選択
する状態へと到達する.局所的レプリケーター動学は,模倣学習を通しての戦
略分布の変化を表現し, をとるプレイヤーと をとるプレイヤーのみから
なる状態においては,協力行動が模倣されやすく,集団の状態は へ向かいに
くい.これが局所的レプリケーター動学と我々の適応プロセスとの間に動学的
オープンソフトウェア を用いて描写し
ている.図 の各軌道は のとき, および
で示されている軌道に近づく. と書く.局所的レプリケーター動学は
によって与えられる.ただしxi の上付き文字のドットは時間微分dxdtiを表し, ˜
A=A−A+At
n である.
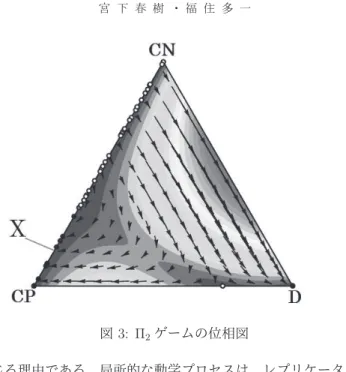
n= 3とする.π2ゲームの∆内における局所的レプリケーター動学の軌道を
位相図として図3に表す.*1図中の黒丸(●)はその点が安定的な定常状態である
ことを表し,白丸(○)は不安定であることを表す.p∈[0,1]をCNとCPをとる
プレイヤーが混在する状態においてCNをとるプレイヤーの割合とする.辺
CN-CP上にCNとCPが混在する安定的な均衡の集合X={peCN+ (1−p)eCP |p≤
d−(b−2)+1
n(a+b−c−d−4)
d−1 n(c+d)
}が存在する.
先に定式化した式(2)の適応プロセスにおいては,Π2ゲームではCPをとるプ
レイヤーのみからなる均衡は安定性をもたず,集団の全プレイヤーがDを選択
する状態へと到達する.局所的レプリケーター動学は,模倣学習を通しての戦
略分布の変化を表現し,CNをとるプレイヤーとCPをとるプレイヤーのみから
なる状態においては,協力行動が模倣されやすく,集団の状態はDへ向かいに
くい.これが局所的レプリケーター動学と我々の適応プロセスとの間に動学的
*1オープンソフトウェアDynamo : http://www.ssc.wisc.edu/ whs/dynamo/を用いて描写し ている.図3の各軌道はn→ ∞のとき,Weibull and Salomonsson (2006)およびSethi and
Somanathan (1996)で示されている軌道に近づく. と書く.局所的レプリケーター動学は
によって与えられる.ただし の上付き文字のドットは時間微分 を表し,
である.
とする. ゲームの 内における局所的レプリケーター動学の軌道を
位相図として図 に表す. 図中の黒丸 ● はその点が安定的な定常状態である
ことを表し,白丸 ○ は不安定であることを表す. を と をとる
プレイヤーが混在する状態において をとるプレイヤーの割合とする.辺
上に と が混在する安定的な均衡の集合
が存在する.
先に定式化した式 の適応プロセスにおいては, ゲームでは をとるプ
レイヤーのみからなる均衡は安定性をもたず,集団の全プレイヤーが を選択
する状態へと到達する.局所的レプリケーター動学は,模倣学習を通しての戦
略分布の変化を表現し, をとるプレイヤーと をとるプレイヤーのみから
なる状態においては,協力行動が模倣されやすく,集団の状態は へ向かいに
くい.これが局所的レプリケーター動学と我々の適応プロセスとの間に動学的
オープンソフトウェア を用いて描写し
ている.図 の各軌道は のとき, および
図3: Π2ゲームの位相図
な差が生じる理由である.局所的な動学プロセスは,レプリケーター動学を用
いるのか,あるいは最適反応動学を用いるのかによって異なる帰結が生じるの
である.今後,我々は離散時間型の局所的レプリケーター動学の定式化を試み
る.そこでCPとCNのみからなる集団状態が長期確率安定性をもつかどうか
は興味深い問題となるであろう.
参考文献
[1] Hilbe, C.“Local replicator dynamics: A simple link between deterministic
and stochastic models of evolutionary game theory.”Bulletin of
図 ゲームの位相図
な差が生じる理由である.局所的な動学プロセスは,レプリケーター動学を用
いるのか,あるいは最適反応動学を用いるのかによって異なる帰結が生じるの
である.今後,我々は離散時間型の局所的レプリケーター動学の定式化を試み
る.そこで と のみからなる集団状態が長期確率安定性をもつかどうか
は興味深い問題となるであろう.
参考文献
135
図 ゲームの位相図
な差が生じる理由である.局所的な動学プロセスは,レプリケーター動学を用
いるのか,あるいは最適反応動学を用いるのかによって異なる帰結が生じるの
である.今後,我々は離散時間型の局所的レプリケーター動学の定式化を試み
る.そこで と のみからなる集団状態が長期確率安定性をもつかどうか
は興味深い問題となるであろう.
参考文献
[2] Kandori, M, Mailath, G J and Rob, R.“Learning mutation, and long-run
equilibria in games.”Econometrica, 61: 29-56, 1993.
[3] Sandholm, B, Dokumaci, E and Franchetti, F. Dynamo: Diagrams for
evolutionary game dynamics : http://www.ssc.wisc.edu/ whs/dynamo/
2016/10/29.
[4] Sethi, R and Somanathan, E.“The evolution of social norms in common
property resource use.”American Economic Review, 86(4): 766-788, 1996.
[5] Weibull, J W and Salomonsson, M.“Natural selection and social
prefer-ence.”Journal of Theoretical Biology, 239: 79-92, 2006.
[6] Young , P.“The evolution of conventions.” Econometrica, 61(1): 57-84,
宮下春樹・
福住多一
(8,0,0) (7,1,0) (7,0,1) (6,2,0) (6,1,1) (6,0,2) (5,3,0) (5,2,1) (5,1,2) (5,0,3) (4,4,0) (4,3,1) (4,2,2) (4,1,3) (4,0,4) (3,5,0) (3,4,1) (3,3,2) (3,2,3) (3,1,4) (3,0,5) (2,6,0)
(8,0,0) 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(7,1,0) 0 1/8 1/8 1/8 5/8 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 (7,0,1) 0 0 1/8 0 0 7/8 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 (6,2,0) 0 1/28 0 13/56 5/28 0 11/56 5/14 0 0 0 0 0 0 0 0 0 0 0 0 0 0 (6,1,1) 0 1/56 0 1/56 3/14 1/8 0 5/56 15/28 0 0 0 0 0 0 0 0 0 0 0 0 0 (6,0,2) 0 0 0 0 0 1/4 0 0 0 3/4 0 0 0 0 0 0 0 0 0 0 0 0 (5,3,0) 0 0 0 11/112 0 0 9/28 5/28 0 0 25/112 5/28 0 0 0 0 0 0 0 0 0 0 (5,2,1) 0 0 0 11/336 1/24 0 11/336 45/112 5/84 0 0 15/112 25/84 0 0 0 0 0 0 0 0 0 (5,1,2) 0 0 0 0 1/24 0 0 5/168 25/84 1/8 0 0 5/84 25/56 0 0 0 0 0 0 0 0 (5,0,3) 0 0 0 0 0 0 0 0 0 3/8 0 0 0 0 5/8 0 0 0 0 0 0 0 (4,4,0) 0 0 0 0 0 0 5/28 0 0 0 11/28 1/7 0 0 0 3/14 1/14 0 0 0 0 0 (4,3,1) 0 0 0 0 0 0 5/112 17/112 0 0 5/112 37/112 5/28 0 0 0 3/28 1/7 0 0 0 0 (4,2,2) 0 0 0 0 0 0 0 13/168 1/21 0 0 3/56 9/28 5/28 0 0 0 1/12 5/21 0 0 0 (4,1,3) 0 0 0 0 0 0 0 0 1/14 0 0 0 1/28 3/8 1/8 0 0 0 1/28 5/14 0 0 (4,0,4) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1/2 0 0 0 0 0 1/2 0 (3,5,0) 0 0 0 0 0 0 0 0 0 0 15/56 0 0 0 0 25/56 5/56 0 0 0 0 5/28 (3,4,1) 0 0 0 0 0 0 0 0 0 0 3/56 3/14 0 0 0 3/56 5/14 1/7 0 0 0 0 (3,3,2) 0 0 0 0 0 0 0 0 0 0 0 3/28 15/112 0 0 0 1/14 9/28 5/28 0 0 0 (3,2,3) 0 0 0 0 0 0 0 0 0 0 0 0 15/112 3/56 0 0 0 1/16 39/112 5/28 0 0 (3,1,4) 0 0 0 0 0 0 0 0 0 0 0 0 0 3/28 0 0 0 0 1/28 25/56 1/8 0
(3,0,5) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5/8 0
(2,6,0) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5/14 0 0 0 0 0 27/56 (2,5,1) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5/84 55/168 0 0 0 0 5/84 (2,4,2) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 11/84 1/4 0 0 0 0 (2,3,3) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3/16 17/112 0 0 0 (2,2,4) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 17/84 5/84 0 0 (2,1,5) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 25/168 0 0
(2,0,6) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(1,7,0) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3/8
(1,6,1) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1/16
(1,5,2) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(1,4,3) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(1,3,4) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(1,2,5) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(1,1,6) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(1,0,7) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(0,8,0) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(0,7,1) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(0,6,2) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(0,5,3) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(0,4,4) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(0,3,5) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(0,2,6) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(0,1,7) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(0,0,8) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
宮下春樹・
福住多一
(8,0,0) (7,1,0) (7,0,1) (6,2,0) (6,1,1) (6,0,2) (5,3,0) (5,2,1) (5,1,2) (5,0,3) (4,4,0) (4,3,1) (4,2,2) (4,1,3) (4,0,4) (3,5,0) (3,4,1) (3,3,2) (3,2,3) (3,1,4) (3,0,5) (2,6,0)
(8,0,0) 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(7,1,0) 0 1/8 1/8 1/8 5/8 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 (7,0,1) 0 0 1/8 0 0 7/8 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 (6,2,0) 0 1/28 0 13/56 5/28 0 11/56 5/14 0 0 0 0 0 0 0 0 0 0 0 0 0 0 (6,1,1) 0 1/56 0 1/56 3/14 1/8 0 5/56 15/28 0 0 0 0 0 0 0 0 0 0 0 0 0 (6,0,2) 0 0 0 0 0 1/4 0 0 0 3/4 0 0 0 0 0 0 0 0 0 0 0 0 (5,3,0) 0 0 0 11/112 0 0 9/28 5/28 0 0 25/112 5/28 0 0 0 0 0 0 0 0 0 0 (5,2,1) 0 0 0 11/336 1/24 0 11/336 45/112 5/84 0 0 15/112 25/84 0 0 0 0 0 0 0 0 0 (5,1,2) 0 0 0 0 1/24 0 0 5/168 25/84 1/8 0 0 5/84 25/56 0 0 0 0 0 0 0 0 (5,0,3) 0 0 0 0 0 0 0 0 0 3/8 0 0 0 0 5/8 0 0 0 0 0 0 0 (4,4,0) 0 0 0 0 0 0 5/28 0 0 0 11/28 1/7 0 0 0 3/14 1/14 0 0 0 0 0 (4,3,1) 0 0 0 0 0 0 5/112 17/112 0 0 5/112 37/112 5/28 0 0 0 3/28 1/7 0 0 0 0 (4,2,2) 0 0 0 0 0 0 0 13/168 1/21 0 0 3/56 9/28 5/28 0 0 0 1/12 5/21 0 0 0 (4,1,3) 0 0 0 0 0 0 0 0 1/14 0 0 0 1/28 3/8 1/8 0 0 0 1/28 5/14 0 0 (4,0,4) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1/2 0 0 0 0 0 1/2 0 (3,5,0) 0 0 0 0 0 0 0 0 0 0 15/56 0 0 0 0 25/56 5/56 0 0 0 0 5/28 (3,4,1) 0 0 0 0 0 0 0 0 0 0 3/56 3/14 0 0 0 3/56 5/14 1/7 0 0 0 0 (3,3,2) 0 0 0 0 0 0 0 0 0 0 0 3/28 15/112 0 0 0 1/14 9/28 5/28 0 0 0 (3,2,3) 0 0 0 0 0 0 0 0 0 0 0 0 15/112 3/56 0 0 0 1/16 39/112 5/28 0 0 (3,1,4) 0 0 0 0 0 0 0 0 0 0 0 0 0 3/28 0 0 0 0 1/28 25/56 1/8 0
(3,0,5) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5/8 0
(2,6,0) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5/14 0 0 0 0 0 27/56 (2,5,1) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5/84 55/168 0 0 0 0 5/84 (2,4,2) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 11/84 1/4 0 0 0 0 (2,3,3) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3/16 17/112 0 0 0 (2,2,4) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 17/84 5/84 0 0 (2,1,5) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 25/168 0 0
(2,0,6) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(1,7,0) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3/8
(1,6,1) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1/16
(1,5,2) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(1,4,3) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(1,3,4) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(1,2,5) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(1,1,6) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(1,0,7) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(0,8,0) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(0,7,1) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(0,6,2) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(0,5,3) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(0,4,4) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(0,3,5) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(0,2,6) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(0,1,7) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
(0,0,8) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Π2 表 Π ゲームにおける推移確率行列
137
ラ
ン
ダ
ム
な
局
所
的
対
戦
構
造
を
も
つ
適
応
プ
ロ
セ
ス
がゲ
ー
ム
の
均
衡
選
択に
与
え
る
影
響
(2,5,1) (2,4,2) (2,3,3) (2,2,4) (2,1,5) (2,0,6) (1,7,0) (1,6,1) (1,5,2) (1,4,3) (1,3,4) (1,2,5) (1,1,6) (1,0,7) (0,8,0) (0,7,1) (0,6,2) (0,5,3) (0,4,4) (0,3,5) (0,2,6) (0,1,7) (0,0,8)
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1/56 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1/8 3/56 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 9/112 3/28 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 5/112 5/28 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 1/56 15/56 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 3/8 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1/28 0 0 0 0 0 1/8 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
61/168 5/56 0 0 0 0 0 5/56 1/84 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1/12 25/84 1/7 0 0 0 0 0 5/84 1/28 0 0 0 0 0 0 0 0 0 0 0 0 0 0 9/112 33/112 5/28 0 0 0 0 0 1/28 1/14 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5/84 61/168 5/28 0 0 0 0 0 1/56 5/42 0 0 0 0 0 0 0 0 0 0 0 0 0 0 5/168 43/84 1/8 0 0 0 0 0 1/168 5/28 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 3/4 0 0 0 0 0 0 0 1/4 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 9/16 0 0 0 0 0 0 0 1/16 0 0 0 0 0 0 0 0
25/56 0 0 0 0 0 1/16 39/112 1/28 0 0 0 0 0 0 5/112 0 0 0 0 0 0 0 25/168 65/168 0 0 0 0 0 5/56 1/4 5/56 0 0 0 0 0 0 5/168 1/168 0 0 0 0 0 0 13/56 2/7 0 0 0 0 0 5/56 3/14 1/7 0 0 0 0 0 0 1/56 1/56 0 0 0 0 0 0 2/7 17/112 0 0 0 0 0 1/14 1/4 5/28 0 0 0 0 0 0 3/112 1/28 0 0 0 0 0 0 95/336 11/168 0 0 0 0 0 5/112 41/112 5/28 0 0 0 0 0 0 1/336 5/84 0 0 0 0 0 0 11/56 0 0 0 0 0 0 1/56 4/7 1/8 0 0 0 0 0 0 0 5/56 0
0 0 0 0 0 0 0 0 0 0 0 0 0 7/8 0 0 0 0 0 0 0 0 1/8
0 0 0 0 0 0 1/2 0 0 0 0 0 0 0 1/2 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1/16 9/16 0 0 0 0 0 0 1/16 5/16 0 0 0 0 0 0 0 0 0 0 0 0 0 0 9/56 15/28 0 0 0 0 0 0 5/56 5/28 1/28 0 0 0 0 0 0 0 0 0 0 0 0 0 15/56 25/56 0 0 0 0 0 0 5/56 3/28 5/56 0 0 0 0 0 0 0 0 0 0 0 0 0 5/14 9/28 0 0 0 0 0 0 1/14 3/28 1/7 0 0 0 0 0 0 0 0 0 0 0 0 0 45/112 3/16 0 0 0 0 0 0 5/112 3/16 5/28 0 0 0 0 0 0 0 0 0 0 0 0 0 3/8 1/14 0 0 0 0 0 0 1/56 5/14 5/28 0
0 0 0 0 0 0 0 0 0 0 0 0 1/4 0 0 0 0 0 0 0 0 5/8 1/8
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1