パネル二項選択モデル 教育 OKUI, Ryo

平成24年度 ミクロ計量経済学

講義ノート5 パネルデータにおける２項選択モデル

このノートでは、パネルデータの分析に使用する２項選択モデルの紹介と、その注意すべ き点を考察する。パネルデータ分析は、個人間の異質性を制御できることが利点であるが、 ２項選択モデルのような非線形モデルでその利点を活かすのは、それほど自明ではない。ま た動学モデルの場合は、初期条件の定式化が必要となるが、いかにしてその定式化を行うか には議論の余地がある。

5.1 パネルデータ２項選択モデル

次のような単純な２項選択モデルを考える。

y_it= 1{x^′_itβ + v_it≥ 0} (1)

i = i, . . . , n (n → ∞); t = 1, . . . T (T ^は固定)^{とする。ここで、} vit|Xi ∼ F

|{z}

正規分布やロジット分布など

(2)

と仮定し、_iについては無作為標本を仮定する。_vitは時系列方向には相関があることを許容 するモデルである。

このモデルの場合、「部分的」最尤推定量を使用することができる。つまり、目的関数を l =

∑n i=1

∑T t=1

[y_itlog F (x^′_itβ) + (1 − y_it) log{1 − F (x^′_itβ)}^] (3)

として、β = arg min lˆ を推定量とするものである。なお、_vitの時系列方向での相関を無視 しているため、_lは真の尤度ではないかもしれない。しかし、_βˆが一致性をもつことは、比 較的容易に示すことができる。

• この方法の問題点は、一致性があっても有効性は担保できていないことがあげられる。 またより本質的な問題として、個人間の異質性を_vitに含めてしまっているため、個人 間の異質性を固定した上での_xitの効果を表現できていないことがある。実際、個人 間の異質性が変量効果で表現でき、モデルが正しいとしても、推定した_βの値は、変 量効果の部分を制御した_xitの効果にはならない。

• ^なお、vitの相関を考慮するため、標準誤差の計算には、自己相関に頑健な標準誤差の 式を使用するべきである。

他にも、線形モデルを使用することもある。モデルは、

yit = x^′_itβ + vit (4)

である。この方法の利点は、線形モデルの手法がそのまま使え、_vitが固定効果を含む場合 や、動学モデルの推定も容易であることである。しかし、線形モデルであるので、_{yit= 1}と なる確率が₀と₁の間に収まらないなどの問題を起こす可能性が高い。

5.2 観測できない異質性を考慮したモデル

パネルデータ分析の利点である、個人間の異質性の制御を行うため、

yit= 1{x^′_itβ + µi+ vit≥ 0} (5) として、個人効果_µiをモデルに含める。ここで、_vit|Xiの分布は仮定しておく。

変量効果 まず、_µiが_Xiと独立であり、その分布がわかっている変量項効果モデルを考え る。つまり、追加的なじょうけんとして、

µi|Xi ∼ N (0, σ_µ²) (6)

と仮定する。なお、必ずしも正規分布を仮定する必要はない。また、

v_i|X_i ∼ N (0, σ_v²I) (7)

を仮定する。

• ^{識別のために、}σ_v²= 1^{という標準化をする。}

ここで考えているモデルは、変量効果プロビットモデルという。

この場合、一致で有効な推定が可能になる。尤度関数の導出のために、_µiについて条件 づけた確率を考察する。それは、

Pr(yi|Xi, µi) =

∏T t=1

Φ(x^′_itβ + µi)^yit(1 − Φ(x^′_itβ + µi))^1−yit (8)

と書ける。しかし、_µiの密度は、_{ϕ(µi/σµ)/σµ}と仮定したので、_µiについて積分をして、 Pr(yi|Xi) =

∫ ^T

∏

t=1

Φ(x^′_itβ + µi)^yit(1 − Φ(x^′_itβ + µi))^{1−yit 1} σµ

ϕ^{( µi} σµ

)

dµi (9)

という確率の表現を得る。 つまり、尤度関数は、

l =

∑n i=1

log Pr(yi|Xi) (10)

と書ける。また最尤推定量β = arg min l^{ˆ は有効である。}

• ^{ここでは、}var(v_it|x_i, µ_i) = 1と仮定した。しかし、時点ごとに異なる分散を許容する ことができる。つまり、_{var(vit|xi, µi) = σ}²_vtと仮定する。ただし、識別のための標準 化として、_σ²_{v1 = 1}と仮定する。

Chamberlainのモデル 変量効果モデルでは、_Xiと_µiが独立であることが仮定されてい た。これは、経済学上の応用では、正当化しにくい仮定である。この問題を緩和するため、 Chamberlain (1980)^はµ_i^を

µi = π + Π^′Xi+ ai, (11)

とモデル化することを提案した。ここで、_ai(µiではない₎が変量効果であると仮定する。例 えば、

a_i|X_i ∼ N (0, σ²_a) (12)

と仮定する。なお、_πと_Πは誘導形の係数と解釈し、特に経済学的な意味づけを行わない。 この場合、確率は、

Pr(yit= 1|Xi, µi) = Φ(β^′xit+ µi) = Φ(β^′xit+ π + Π^′Xi+ ai) (13)

と書ける。つまり、

Pr(y_it = 1|X_i) =

∫

Φ(β^′x_it+ π + Π^′X_i+ a_i) ¹ σ_a^ϕ

( a σ_a

)

da (14)

であり、尤度関数は、 l =

∑n i=1

log

∫ ^T

∏

t=1

Φ(β^′xit+ π + Π^′Xi+ ai)^yit{1 − Φ(β^′xit+ π + Π^′Xi+ ai)}^(1−yit(15)⁾

× ¹ σa

ϕ^{( a} σa

)

da (16)

となる。つまり、_aは積分をとることで消している。尤度関数を最大化して、(β, π, Π, σa)^を 推定する。

• 識別が可能である理由は、_Xiがそれぞれの_iについて同じように影響を与える一方で、 xitは時間とともに変動することである。したがって、時間を通じて変動しない回帰変 数の係数は識別できない。

• π + Π^′Xi^{の代わりに、}π + Π^′x¯i を使用することもよくある。Mundlak (1978)^による 提案である。推定すべき変数の数を減らすことが可能であり、またバランスのとれて いないパネルデータの場合にも有用である。

• vitの分散不均一性も考慮できる。例えば、

v_i1 ∼ N (0, 1) (^標準化) (17)

v_i2 ∼ N (0, σ₂²) (18)

. . . (19)

v_iT ∼ N (0, σ_T²) (20)

と仮定する。

5.3 固定効果ロジットモデル

次に、_µiについては何も仮定しない、固定効果_(FE)モデルを考える。 F ^をvの分布として、尤度関数は

l =

∑n i=1

∑T t=1

[yitlog F (x^′_itβ + µi) + (1 − yit) log{1 − F (x^′_itβ + µi)}^] (21)

を考える。しかし、一般に、この関数から_µiを取り除いて推定することはできない。これ はモデルの非線形性による。

• 静学的ロジットモデルにおいては、固定効果を取り除くことができるが、それは、特殊 な状況であり、またロジットモデルでないと取り除くことはできない。Chamberlain (2010)^{ならびに、}Magnac (2004)^{を参照せよ。}

もし、_T が固定されている状況で、_{(β, µ1}, . . . , µn)^{について、}lを最大化しても、一致性の ある推定量は得られない。これは、母数のうち_µiの次元が無限であることから来る問題で あり、“incidental parameter problem (^{付随パラメーター問題})”^{あるいは、}‘Neyman-Scott (1948)^問題”^{と呼ばれる。}

• ^{なお、線形モデル、}

y_it = βx_it+ µ_i+ v_it (22)

の場合は、_yitを_xitに回帰しその時に各人ごとに定数項ダミーを加えると固定効果推 定量を得られる。これは一致性をもつ。しかし、_µiを一致性をもって推定することは できない。

T が無限に行く状況では、固定効果推定をすることができる。これは次のノートで議論 する。

ただし、ロジットモデルの場合には、固定効果を入れたモデルの推定をすることができ る。ここでは、条件付きロジットモデル(Chamberlain (1980))^{を考える。}

一般理論 まず、一般的な固定効果を消去する方法から議論する。 今、次のような尤度関数があるとする。

l( y

|{z}

{yi1,...,yiT}

|X, θ, {µi}ⁿ_i=1). (23)

重要なポイントは、_{µi}ⁿ

i=1^{の十分統計量(S)}を得ることである。つまり、

l(y|X, S, θ, {µi}ⁿ_i=1) = l(y|X, S, θ) (24) となるような統計量_Sがあるとよい。

• 例えば、誤差項が正規分布に従う線形モデル、 yit= β^′xit+ µi+ vit

|{z}

正規乱数

(25)

の場合は、

∑T

t=1^{yit = Siがµi}の十分統計量となる。このモデルの場合、固定効果推 定量が、条件付き最尤推定量となる。

パネル固定効果ロジットモデル 次に、今の議論の焦点である、２項選択モデルについて考 える。次のパネル固定効果ロジットモデル、

Pr(yit= 1|Xi, µi) = ^e

β^′xit+µi

1 + e^{β′xit+µi (26)}

を考察する。_Tは固定と仮定する。 このモデルでは、

∑T

t=1^{yitがµiの十分統計量となる。}

簡単化のために、_{T = 2}の場合を考える。つまり、_{Si = yi1+ yi2}となる。以下では、_Xi と_µiとに条件づけていることは省略する。次の確率を計算する。

Pr{(y_i1, y_i2) = (∗, ∗)|Si}. (27) もし、_{Si= 0}あるいは、₂の時は、それぞれ、_{(yi1, yi2) = (0, 0)}あるいは、_{(1, 1)}となる。つ まり、この時は分布は退化すし、尤度への貢献はない。

したがって、_{Si= 1}の場合のみを考える。すると、

Pr{(y_i1, y_i2) = (0, 1)|Si = 1} (28)

= ^{Pr{(yi1, yi2}) = (0, 1)}

Pr{(y_i1, y_i2) = (0, 1), (1, 0)} ⁽²⁹⁾

=

1 1 + e^β′xi1+µi

e^β′xi2+µi 1 + e^β′xi2+µi 1

1 + e^β′xi1+µi

e^β′xi2+µi 1 + e^{β′xi2+µi +}

e^β′xi1+µi 1 + e^β′xi1+µi

1 1 + e^β′xi2+µi

(30)

= ^e

βxi2+µi

e^βxi2+µi+ e^{βxi1+µi (31)}

= ^e

β˙xi2

1 + e^{β˙xi2 (32)}

となり、_µiは消える。なお _{˙xi2= xi2− xi1}としている。よって、条件付き対数尤度関数は、 l =

∑n i=1

[

1_{{(yi1, yi2}) = (0, 1)} log

( e^β˙xi2 1 + e^β˙xi2

)

+ 1{(yi1, yi2) = (1, 0)} log

( 1

1 + e^β˙xi2 )]

(33)

となる。β = arg max l^ˆ は一致性をもつ。なお、_β^ˆは固定効果を母数とした固定効果推定で はない。その違いについては、Abrevaya (1997)^{を参照せよ。}

• ^{以上の方法では、}β^ˆのみを得ることででき、_µiについは未知のままである。_βのみが わかっている状況ではどのような分析が可能であるかが、ここでの論点である。以下 で示すように、オッズ比については、_βのみの知識で、分析が可能になる。オッズ比は

オッズ比₌

Pr(yit= 1) Pr(yit= 0) ^{= e}

βxit+µi

(34)

である。よって、

log(^オッズ比) = βx_it+ µ_i (35)

から

∂

∂xit

log(^オッズ比) = β (36)

となり、オッズ比に_xitの与える影響は_βで表現できることがわかる。 しかし、限界効果

∂

∂xit

Pr(yit = 1) (37)

を得ることはできない。そのためには、_µiを既知とするか、_µiの分布を仮定₍つまり 変量効果にする₎し、積分をとって消してしまうしかない。

5.4 動学的離散選択モデル

この節では、動学的なモデルを考える。具体的には、

Pr(yit= 1|xi, yi,t−1, . . . µi) = F (x^′_itβ + αyi,t−1+ µi) (38) のように、ラグ付き被説明変数が説明変数としてつかわれるモデルである。このようなモデ ルを考える目的は、状態依存と個人の異質性とを区別したいことである。

• α: (^真の)状態依存を表現している。

• µi: 見せかけの状態依存を表現している。

このモデルを推定する際に問題となるのは、初期値の_yi0をどのように取り扱うかである。 変量効果推定 まず_µiを固定されているものとして扱い、そして後ほど積分をとって消すとい

う、これまで考えてきた方法を考える。まず、各個人の尤度への貢献は、_{f (yi0, yi1}, . . . , y_iT|x_i, y_i0, µ_i) = f (yi1, . . . , yiT|xi, yi0, µi)f (yi0|xi, µi)である。このうち最初の項は

f (y_i1, . . . , y_iT|xi, y_i0, mui) (39)

= f (yiT|y_i1, . . . , yi,T−1^{, x}i, y_i0, µi) × f (y_i1, . . . , yi,T−1^|xi, y_i0, µi) (40)

=

∏T t=1

f (yit|y_i0, y_i1, . . . y_i,t−1, xiµi) (41)

=

∏T t=1

F (x^′_itβ + αy_i,y−1+ µi)^yit × (1 − F (x^′_itβ + αy_i,y−1+ µi))^1−yit (42)

≡ A(µ_i) (43)

と書ける。ここで、_Gを_µiの分布として、単に

∫

A(µ)dG(µ), (44)

として積分を取る方法は、正当化されない可能性がある。なぜなら、初期値の分布_{f (yi0|xi, µi)} を無視しているからである。この方法でうまくいくのは、_µiと_yi0が独立の時である。もし そうでないなら、最尤推定量は一致性をもたない。

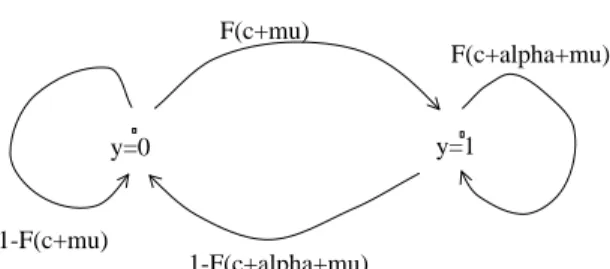
図_1: マルコフ連鎖

y=0 y=1

1-F(c+mu)

1-F(c+alpha+mu)

F(c+alpha+mu) F(c+mu)

初期値の取り扱い方 したがって、初期値が_µiと相関がある場合も考慮する必要がある。以 下の議論は、Heckman (1981)^やHsiao (2003)を参考にしている。二つの方法を紹介する。

1. yの定常分布を使用する方法。いま、

Pr(y_it= 1|y_i,t−1, . . . , µ_i) = F (c + αy_i,t−1+ µ_i) (45) であるとする。この時、_µiを固定すると、_yitはマルコフ連鎖になっている。したがっ て、その定常分布を_{p(c, α, µ¯ i)}あるいは_p¯とすると、それは、

(1 − ¯p)F (c + µi) + ¯pF (c + α + µi) = ¯p (46)

→ ¯p = ^{F (c + µi)}

1 + F (c + µi) − F (c + α + µi) ⁽⁴⁷⁾ である。よって、

∑n i=1

log

∫

A(µ)¯p(c, α, µ)^yi0(1 − ¯p(c, α, µ))^1−yi0dG(µ) = l (48)

として尤度を計算する。

この方法の欠点は、共変量の_xiがあった時に、どうやって定常分布を見つけるのかが 自明ではないことである。

2. Chamberlain^{式のやり方}(Heckman^{の方法である。}) 次の誘導形を考える。

Pr(yi0 = 1|Xi, µi) = F (π + Π^′Xi+ γµi), (49) ここで、_{(π, Π, γ)}は誘導形の係数である。

すると、

∑n i=1

log

∫

AF (π + Πxi+ γµi)^yi0(1 − F )^1−yi0dG(µi) (50)

となり、尤度が計算できる。

応用例 Hyslop (1999)による女性の労働参加の研究は、動学パネルモデルの重要な応用例 である。なお、_Hyslopは_vitが

vit= δv_i,t−1+ ηit. (51)

のように_AR(1)に従うモデルも考える。この場合、尤度関数を得るのは難しい。なぜなら、

ϵi = (ϵ_i1, . . . , ϵ_i,T)についても積分をとる必要がある。_{T = 4}なら、数値積分も難しく、シ ミュレーション推定をする必要がある。

動学的パネルロジットモデル Chamberlain (1985)^やHonore and Kyriazidou (2000)^に動 学的固定効果パネルロジットモデルの推定が議論されている。

5.5 シミュレーション推定

パネルデータにおける離散選択モデルの推定にはシミュレーションが必要となることが多 い。この問題の場合には、前のノートで紹介した_GHKシミュレーターが有用である。

考えるモデルは、

yit = 1{x^′_itβ + ϵit> 0}, (52) ϵ_i =



 ϵ_i1 . . . ϵ_iT



 ∼ N (0, Ω) ⁽⁵³⁾

であり、_{(yit, xit)}が観測される。このモデルは、_Ωを適切に定義することにより、変量効果 の入ったモデルも含んでいる。ここで、_{Ji ≡ (yi1}, . . . , y_iT)^かつθ = (β, Ω)^{と表記して、次} の確率

Pr{J_i|X_i, θ} (54)

を評価する必要がある。

いま、_Jiという事象と整合的な_ϵitの値は、

(2y_it− 1)ϵ_it≥ (1 − 2y_it)x^′_itβ (55) を満たす必要がある。そこで、シミュレーションに当たっては、上の不等式を満たすような 分布から_GHKシミュレーターによって加重サンプリングする。

v^を(1−2yit)ϵit+(1−2yit)x^′_itβ^をt番目の要素としてもつベクトルとすると、v ∼ N (a, Σ) である。なお_aはその_t番目の要素が_{(1 − 2yit)x}^′_itβであるベクトルである。_vは正規分布で

あり、_{v ≤ 0}となる条件の下での加重サンプリングは_GHKシミュレーターがまさにしてい

ることであるので、前回のノートの議論がそのまま成り立つ。

参考文献

[1] J. Abrevaya. The equivalence of two estimators for the fixed effects logit model. Economics Letters, 55:41–43, 1997.

[2] G. Chamberlain. Analysis of covariance with qualitative data. Review of Economic Studies, 47(1):225–238, 1980.

[3] G. Chamberlain. Heterogeneity, omitted variable bias, and duration dependence. In J. Heck- man and B. Singer, editors, Longitudinal Analysis of Labor Market Data, pages 3–38. Cam- bridge University Press, 1985.

[4] G. Chamberlain. Binary response models for panel data: Identification and information. Econometrica, 2010(1):159–168, 2010.

[5] C. Gourieroux and A. Monfort. Simulation-based inference: A survey with special reference to panel data models. Journal of Econometrics, 59:5–33, 1993.

[6] J. J. Heckman. The incidental parameters problem and the problem of initial conditions in estimating a discrete time-discrete data stochastic process and some monte carlo evidence. In C. Manski and D. McFadden, editors, Structural Analysis of Discrete Data with Econometric Applications. MIT Press, 1981.

[7] B. E. Honor´e and E. Kyriazidou. Panel data dicrete choice models with lagged dependent variables. Econometrica, 68(4):839–874, 2000.

[8] C. Hsiao. Analysis of Panel Data. Cambridge University Press, 2003.

[9] D. Hyslop. State dependence, serial correlation and heterogeneity in intertemporal labor force participation of married women. Econometrica, 67(6):1255–1294, 1999.

[10] T. Magnac. Panel binary variables and sufficiency: Generalizing conditional logit. Economet- rica, 72(6):1859–1876, 2004.

[11] Y. Mundlak. On the pooling of time series and cross section data. Econometrica, 46:69–85, 1978.

[12] J. Neyman and E. L. Scott. Consistent estimates based on partially consistent observations. Econometrica, 16:1–32, 1948.