J27 e IEEE TC 1982 6

TABLE I

NUMBEROFCODE WORDS FOR SINGLEERROR-CORRECTING CODES

CODE ANCODE SYMMETRIC ERROR-

LENGTH CORRECTINGCODE

NUMBEROF NUMBEROF 71. A CODEWORDS CODEWORDS [6]

10 11 94 72

12 13 316 256

18 19 13798 9728

28 29 9256394 8388608 36 37 1857283156 1275132482

1S an integer in a radix-2 representation. Therefore, the set defined in(2) and (3)isthe set of integers divisible by A, that is an AN code. The AN code can be stated in the form of a theorem.

Theorem: When A is an odd prime and 2 is a primitive element of a primefield GF(A), an AN code whose range is limited to 0 _ N _ (2A- -1

)/A

is capable of correcting a single asymmetric error. The code length n is n⁼A ^-1 and the number of code words M is

M⁼ (2A- ^- 1)/A + 1.

In fact, the residue of the erroneous code word modulo A is equal to the residue of the error value,

2i

modulo A. Since 2 is a primitive element, there is a one-to-one mapping between the set of integers

12iIO

^{_ i_ A-}

²¹

^{and theset}of residues

_j2i

mod A

_I0

^<i^< A^-

_21.

Therefore, the AN code is capable of correcting a single asymmetric error.

1II.

DISCUSSION

The single asymmetric error-correcting AN codes with A being prime and2 being primitive in GF(A) provide a greater code length n⁼A ^-1 against (A^-1)/2 for symmetric case. They are linear and cyclic since (2A1 ^- 1) isdivisible by A. The numbers ofthe code words of the single asymmetric error-correcting AN codes are shown in Table

1.

As shown in Table I these ANcodes have more code words than single symmetric error-correctingcodes of the samecodelength. Since these AN codes are cyclic, error correction can bemadeusing the decoding methodfor the arithmeticerror-correctingcyclicAN codes. In a code word, binary digits are arrangedin thedecreasing order of weight from left to right. The residueof an erroneouscode word modulo A is computed as cyclically shifting thecodeword to the right. If the residue of the code word shifted i times is1, the error value is

2i.

Then the AN codes discussed are suitableforpractical applications to asymmetric channels, such as LSI memory protec- tion.

REFERENCES

[I] S. D. Constantin and T. R. N. Rao, "On the theory of binary asymmetric error correcting codes,"_Inform.Contr., vol. 40, pp. 20-36, 1979. [2]. R. J. McEliece andE.R. Rodemich, "The Constantin-Rao construction

for binary asymmetricerror-correctingcodes," Inform. Contr., vol. 44, pp. 187-196, 1980.

[31 R. R. Varshamov, "A class of codes for asymmetric channels and a problem from the additive theory of numbers," IEEE Trans. Inform. Theory, vol. IT-19, pp. 92-95, Jan. 1973.

[4] R. J. McEliece, "Comment on 'A class of codes for asymmetric channels and a problem from the additive theory of numbers,'"IEEE Trans. In- form. Theory,vol.IT-19,p. 137, Jan. 1973.

[5] T. R. N. Rao, ErrorCodingfor Arithmetic Processors. New York: Academic, 1974.

[6] F. J. MacWilliams and N. J. A. Sloane, The Theory ofError-Correcting Codes. Amsterdam, The Netherlands: North-Holland, 1977.

TheComplexity of Fault DetectionProblems for Combinational LogicCircuits

HIDEO FUJIWARA AND SHUNICHI TOIDA

Abstract-Inthiscorrespondence we analyze the computational complexity of fault detectionproblems for combinational circuits and propose an approach todesign for testability. Although major fault detection problems have been known to be in generalNP-complete, they were proven for rather complex circuits. In thiscorrespondence we show that these are still NP-complete even for monotone circuits, and thus for unate circuits. We show that fork-level(k 2 3) monotone/unate circuits these problems are stillNP-complete,but that these are solvable in polynomial time for 2-levelmonotone/unatecircuits. A class of circuits for which these fault detection problems are solvable in poly- nomial time is presented.Ripple-carry adders, decoder circuits, linear circuits, etc., belong to this class. A design approach is also presented in which an ar- bitrary given circuit is changed to such an easily testable circuit by inserting a few additional test-points.

IndexTerms-Combinational circuits,computational complexity,design for testability, fault detection, polynomial algorithms, test generation.

I. INTRODUCTION

Because of theincreasing circuit density in LSI/VLSI chips, the fault detectionproblem is becoming more difficult, and thus anef- ficient test generation for logic circuits is a matter of prime concern [1]-[3]. Unfortunately, however, major fault detection problems are known to be NP-complete in general [4], [5]. Hence, it appears very unlikely that the fault detection problems can be solved by a poly- nomial timealgorithm. One general approach to this problem is de- signing easily testable circuits, i.e., design for testability. Many studies have been reported for designing logic circuits for which test sets are easily obtainable [3], [6]-[19].

In this correspondence we show that fault detection problemsare NP-complete for k-level (k> 3)monotone/unate circuits although these circuits are known to be easy to test [1 5]-[ 19]. The_proofpre- sented here is much simpler than that of [4]. It is also shown that test generation problem for monotone/unate circuits is NP-complete even if the circuits under tests are known to be irredundant. After analyzing the complexity of fault detection problems, we present a classof cir- cuits for which these problems are solvable in polynomial time. Ripple-carry adders, decoder circuits, linear circuits, etc., belong to the above class. A design approach is then presented in which an ar- bitrary given circuit is changed to such aneasilytestable circuit by inserting a few additional test-points.

II. SATISFIABILITY PROBLEMS

The firstNP-complete problem was reported by Cook [20], which is usually referred to as the satisfiability problem (SAT, for short). We give a brief description of this problem in the following since we need it in our discussion of NP-completeness of fault detection problems. For definitions ofNP-completeness see [5].

A literal is either x orx for somevariablex, and a clause is a sum ofliterals.ABoolean expressionissaidto be inconjunctive normal form (CNF) if it is a product of clauses. A Boolean expression is satisfiable if and only if there exists some assignment of0'sandl's to the variables that gives the expression the value 1. Then theSAT problem is specified as follows.

Manuscript received July 16, 1981; revised January7,1982.This workwas supported in part by NSERC of Canada Grant A7396.

H. Fujiwara is with the Department of Electronic Engineering, Osaka University, Osaka, Japan.

S. Toida is with theDepartment ofSystems Design,UniversityofWaterloo, Waterloo, Ont., Canada.

0018-9340/82/0600-0555$00.75 ©) 1982 IEEE

Satisfiability (SA T):Is aBoolean expression satisfiable? Theorem 1 (Cook's Theorem [20]): SAT is NP-complete. Anexpressionissaidto beclause-monotone if eachofits clauses contains either only negated variablesoronlyunnegatedvariables. The satisfiabilityfor clause-monotone expressions (CM-SAT, for short) is also NP-complete.

Theorem 2: CM-SAT is NP-complete. Forproofsof Theorems 2-4 see

_[231.

Consider a Boolean expression in conjunctive normalformEwith variables xl,X2, * * *,

_xp

and clausesCl,^C2,--*, Cq. A clause

_Ci

is said to cover a clause

_Cj

(written

Ci

-

_Cj)

if allliterals in

_Cj

are containedin

_Ci.

Anexpression E issaidtobe reduced if no clause in theexpressioncoversanother. Thesatisfiabilityfor reduced clause- monotoneBooleanexpressions(RCM-SAT,for short) is also NP- complete.

Theorem3: RCM-SAT is NP-complete.

AlthoughSAT, CM-SAT, and RCM-SAT are all NP-complete, thesatisfiabilityproblem issolvablein polynomial timeifaBoolean expressionis monotoneorunate. Anexpression issaidtobe monotone if it contains only unnegated variables. An expression is said to be unate ifeach variable iseither only negatedoronlyunnegated. The satisfiability problems formonotone expressionsand unate expres- sions(M-SATandU-SAT, forshort, respectively) have been shown tobesolvableintime0(l),where I is the lengthofanexpression.

Theorem4:M-SATand U-SATaresolvable in time0(l),where I is thelength ofanexpression.

III. COMPLEXITY OF FAULT DETECTION

In thiscorrespondenceweshall beconcernedwithmultiinputand multioutputcombinational circuitscomposed ofAND, OR, NAND, NOR, andNOTgates.

First,weconsider thefollowingdecisionproblems.

FaultDetection(FD,for

short):

Cana

single

stuckfault be de- tectedbyinput-output experiments?

Irredundancy (IR):Is acombinational circuit Cirredundant (i.e., canallsinglestuckfaults bedetected)?

Ingeneral, FD and IRareboth knowntobeNP-complete

[4].

^In thissectionweshow that theseproblems^arestillNP-complete^even for k-level (k ^> 3)

monotone/unate

circuitsalthough these are solvableinpolynomial^timefor2-level

monotone/unate

circuits.A circuitissaidtobe ofk-levelif the maximum numberof gates except NOTgatesalonganypath fromprimaryinputstoprimaryoutputs isk.We. shallusethefollowing abbreviations:

kM-FD: FD for k-levelmonotonecircuits, kU-FD:FDfor k-levelunatecircuits, kM-IR:IRfor k-levelmonotonecircuits, kU-IR: IRfork-levelunatecircuits. Webegin with thefollowingtheorem.

Theorem5: 3M-FDand 3U-FDareNP-complete.

Proof: Sincemonotonecircuitsarealso unate, it issufficientto provethat3M-FD isNP-complete.

Obviously, 3M-FD is in NP. _Hence,weneedtoshowthatsome NP-complete problemispolynomially transformable^{to3M-FD. We} shalltransform CM-SATto3M-FD.

Givenany clause-monotoneexpressionEwithvariables x1,X2,**,

xp

^{andclausesC1, C2,--*,}

Cq,

we construct a3-levelmonotonecircuit Qiasfollows(see Fig. 1).

Without loss ofgenerality,we assumethatC1, C2, ^,

Ck

^arethe clauseswithnegatedvariablesand Ck+1,

Ck+2,...

^,

Cq

^arethe clauses with

unnegated

variables.

Step

1:ConstructANDgatesA1,

A2,.*.

^,

Ak corresponding

tothe clausesC1, C2,* * *,

_Ck

with

negated

variablessothateachANDgate Aihas theinputvariables of

_Ci.

forexample,supposeaclause

_Ci

=

- v b v c, then the output of

Ai

isa b^-c.

Step^2:ConnecttheaboveANDgatesto ORgates G1asshownin Fig. 1.

Step3: ConstructOR_gates

_{01, 02, *,.°q-k}

O

corresponding

^tothe

x₁ ... x_P

Fig.1. -3-level monotonecircuitQl.

clausesCk+ 1, Ck+2,^--*,Cq withunnegatedvariables. Forexample, the output of

Oi

^isa v b v cifthe clause

Ci

⁼a v b v c.

Step4:Connect all theORgates

01,

02, ,

_Oq-k,

and G1 toAND gateG2asshown inFig. 1.

Inthis circuit

Q1,

astuck-at-I faultatthe output of gateG1, is detectable if andonlyif there existsatest suchthatallthe outputs ofANDgatesA1, A2, *^-*,_Akare 0andall theoutputs ofORgates

_01,

02,^--*, Oq-k^are1.Hence,^{the fault}G1s-a-Iis detectable if and

_only

ifthe given expressionEissatisfiable.

Theaboveconstruction can be carried out inanamountoftime linear in p and q.Therefore, CM-SAT ispolynomially transformable

to3M-FD. _Q.E.D.

Theorem6:3M-IRand3U-IR areNP-complete.

Proof: Obviously,3M-IRis in NP. We show thatRCM-SAT ispolynomially transformableto3M-IR.

Givenanyreducedclause-monotoneexpressionEwithvariables

XI,

^{X2, ,xp} and clausesC1, C2,^-*-,

_Cq,

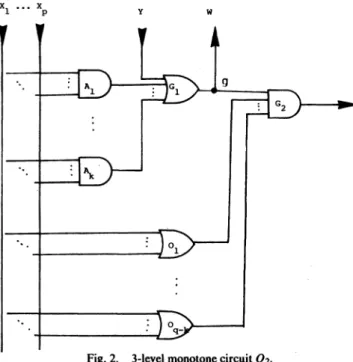
we construct a3-level monotonecircuit Q2asfollows(see Fig. 2).

Step1:Constructthe3-levelmonotonecircuit

_Q,

of Fig.Iin the mannermentionedintheproofof Theorem 5.

Step2:Addaprimaryinputy anda

primnary

outputwtotheOR gate G1asshown inFig.2.

This construction canbeperformed in timelinear in p andq. Hence, thereremainstoprove thatQ2 iS irredundantif andonly if Eissatisfiable.

Suppose^thatEisnotsatisfiable.Thisimpliesthat thereexistsno testsuchthatall the outputs of theANDgatesA1,A2, *^-*,_Akare0 and alltheoutputsoftheORgates

_01,

02,^-

.,

*

_Oq-k

^are1,asshown intheproof ofTheorem 5. Hence,astuck-at-I faultatlineg,which isaninputof gateG2,is notdetectablebecause there existsnotest such that g⁼0and all otherinputs of G2^are1.Thisimplies thatQ2 isnotirredundant.

Conversely,suppose thatEissatisfiable, that is, there existsatleast one testsuchthatall the outputs of theANDgatesA1, A2,^--*,

Ak

^are 0andall the outputsoftheORgates

01, 02,

* **,

_Oq-k

are1.Weshow thatQ2isirredundant by constructingtestsforallsingle faults.

1) Todetecta s-a-I faultaty, w,andthe outputof G1, choosea testsuch that all the outputs ofANDgatesA1,

A2,.*.

^,

Ak

^are0and

y ⁼0.

2) Todetectas-a-0faultaty, w, andthe output ofG1,choose a testsuchthat all the outputs ofANDgatesA1,

A2,.*.

^,Ak^are0and y ⁼ 1.

X_.1...x_{P y}

Fig.2. 3-levelmonotonecircuit Q2-

3) To detectas-a-0 faultatg_{and theoutputof}G2,_choosea_test

such thatall theoutputsofOR_{gates 012,} q-kare 1 and y ^{= 1.}

4) To detecta s-a-^I faultatgand the output ofG2,chooseatest suchthat all theoutputsofANDgatesA1, A2,^-* *,_Akare0,all the outputsof^ORgates01, 02, - - -.Oq-kare¹andy⁼0. The existence ofthistestisguaranteed bythehypothesis.

5) Todetectas-a-0 faultattheinputsand the output ofANDgate Ai^{(1 Si<k),chooseatest}such that all theinputsof_Aiare1,all theoutputsofthe otherANDgates

_Aj

(j ⁼ 1, 2, * * *, k;^j 5 ⁱ⁾are0 andy=_{0. This}testcanbe found since E is reduced.

6) To detectas-a-I faultatan_inputh and the outputofAND_gate

Ai^{(1 <i< k),chooseatest}such that h ⁼0,all the otherinputsof Ai^{are1,all theoutputsof theotherANDgates}

_Aj

(j⁼ 1,_2,**;,k;

j

^{5 i)are0,andy =0. Thistestcanbe foundsince E isreduced.}

7) To detect^as-a-Ifaultattheinputsand outputs ofORgateO0

(1 <i <q^-k),choose^atestsuch that all theinputsof _0iare0,all theoutputsof other^ORgates

_Oj

(j -1,2,*^{- ,}q^- k; j ^i)are1, andy ⁼ 1. Thistestcanbe found since E is reduced.

8) Todetectas-a-0fault atan_inputhand theoutputofORgate

Oi

(1 ^<i< q^- k),^chooseatest such that h=1,all the other_inputs of

_Oi

are0,all the outputsof the other OR_gates

_Oj

_(j= 1, 2,* * ^,

q ^- k;

_fi)

are 1, and y = ^1. This testcan be found since E is

reduced. ^Q.E.D.

Now^wehave shown that the fault detectionproblemand the ir- redundancy test problem are both NP-complete even for 3-level monotone/unatecircuits. These results alsoimplythat the fault de- tection problemand theirredundancy testproblem^are ingeneral NP-complete.It^wasreported earlier that FD and IRareboth NP- complete byIbarra and Sahni[4].However,theproofin

_[4]

is rather longandcomplicated.Ascomparedwiththis,theproofofTheorem 6 in thiscorrespondenceissimplersincewe_onlyuse a_simplercircuit Q2than the circuit Q in [4].

Next,^weconsider thefollowing testgeneration problemwitha more_stringentcondition.Suppose^weknow thatacircuit Cismon- otoneand irredundant and^wewishtoknow howlongitwilltaketo findatestfora_givenfaultinC. Thefollowingtheoremshowsthat thisproblemis stillNP-complete.

Theorem 7: Theproblemoffinding^atest todetect^agivenfault finan_arbitrarymonotoneand irredundant circuit C is NP-com-

plete.

Proof:It sufficestoshow thata_polynomialtimealgorithmfor finding^atestforfinCcanbe usedtodevelop^apolynomialtime al- gorithmforsolving3M-FD.

Assume that we have a polynomial time algorithm A that finds a testfor a given fault f in an arbitrary monotone and irredundant circuit C. Using this algorithm, we can construct a polynomial time algorithm that solves 3M-FD as follows.

AlgorithmA

Input:Anirredundant monotone circuit C and a single stuck fault Output: A test todetectf inC.

Let

_p(-)

be thepolynomial time bound of A. Algorithm B

Input:A 3-level monotone circuit C' and a single stuck faultf'. Output: "yes" if there is a test to detectf', and "no" otherwise. Method:

Step 1: Apply Algorithm A tof' and C'.

Step 2: If A does not halt onf' and C' after

p(-)

steps,there is no testforf' and the answer is "no."

Step 3: If A halts onf' and C' in less than or equal top(-) steps, then checkwhether or not the output is a testforf'.If it is a test for f', then the answer is "yes." Otherwise, there is no test forf', and the

answer is"no." Q.E.D.

Although all the above mentioned problems are NP-complete for k-level (k 2 3) monotone/unate circuits, we can see that such problems are solvable in polynomial time for k = 2.

Theorem 8: 2M-FD and 2U-FD are solvable in time complexity O(m 2), where m is the number of lines in a circuit.

Theorem9: 2M-IR and 2U-IR are solvable in time complexity O(m3).

For proofs of Theorems 8 and 9, see [23]. A Designfor Testability

The result of Theorem 8indicates that by using 2-level mono- tone/unate circuits it is possible to convert any circuit into an equivalent circuit for which a test set is obtained in time complexity O(m 2). One realization of a 2-level logic circuit is a programmable logic array (PLA) which is very well suited toLSI/VLSI.A PLAhas astructureshown in Fig. 3(a), which is composed of AND array, OR array, anddecoders. Fig. 3(a) shows a PLA with 1 bit decoders. The augmented PLA shown in Fig. 3(b) can realize a 2-level monotone circuit by resetting allflip-flopsof ashiftregister. Then the equivalent monotonePLA can betestedintime complexity O(m2). The Ex- clusive-ORgatesand theshift register can be tested by using extra AND termintime complexity 0(n) where n is the number of in- puts.

IV. POLYNOMIALTIMECLASS

Wehaveshown that thefaultdetection problem is still NP-com- pleteeven formonotone/unatecircuits. However, there are many circuitsfor whichthefault detectionproblem canbe solved in poly- nomialtime,e.g.,linear circuits,decodercircuits, parallel adder, etc. In thissectionwe present aclassofcircuitswhich contains theabove circuitsandfor which thefault detectionproblem canbesolvedin polynomial time of the number of linesinthe circuits.

Afan-out-pointPiscalledahead fan-out-pointif there is a path fromaprimary inputtop withoutencountering any other fan-out- point.

Acombinational circuitC issaidtobek-head-fan-out-bounded if C can be partitioned intosubcircuits,calledblocks, B1,B2,*** B, such that:

1) there isnoreconvergentpath in the interconnection of blocks B1, B2,^---,B1,and

2) for each block_{Bi (1} <i<_t)the number of headfan-out-points inBiplus the number of linescoming into

_Bi

from other blocks except primary inputsisat mostk.

Notethattheremay existparallellinesbetween blocks (see Fig. 4).Example1:Considera_parallelbinary adder ofp bits constructed by cascadingp stages of one-bitfulladderscalled ripple-carry adder. Fig.5(a)shows a p stage ripple-carry adder and Fig. 5(b) shows an implementationfor one-bitfulladder with three head fan-out-points.

NO. 6, 1982

xl

v _X,

LIF

AND v

ARRAY :

'>>|~~~~~~~~~~~~~ )

OR _{. ~} OR

ARRAY ARRAY

(a) (b)

Fig. 3. Easily testable PLA. (a)PLA.(b) Augmented PLA

*Prinmry

Ouut

Fig.4. k-head-fan-out-bounded circuit.

CO

ai bi

(b)

c_p

(a)

Fig. 5. Ripple-carryadder. (a)Ripple-carryadder.(b)^{Full adder}(FA). Partition this adder^sothat each block correspondstoafull adder. Then^weseethat the ripple-carry adder is^a3-head-fan-out-bounded circuit.

Example 2:Consider agate-minimum p-bit parallel adder de- signed byLai andMuroga [221whoseblockdiagramis shown inFig. 6. This circuit isa6-head-fan-out-bounded circuit.

Example3: The Exclusive-ORtreerealization ofalinear function isa2-head-fan-out-boundedcircuit since each Exclusive-ORgate^can be realizedbytwoheadfan-out-points.

Example4: Ap-bitdecodercanbe realizedby^acircuit with 2P

AND _gates andp head fan-out-points. Hence, it is ^ap-head-fan- out-bounded circuit.

Everycircuitcanbedecomposedintosubcircuits, calledfan-out- free circuits,which donotcontainfan-out-points. Webeginwitha

lemma for fan-out-free circuits. ForproofsofLemmas¹ and2,^see

[23].

Lemma 1: Let C beafan-out-free circuitwithinputsx1,x2,

xnand output^z.Supposethatthevalues0,1, D,and^Dare_assigned

atZ andsomeoftheinputsofC.Then there isan0(m) algorithm

tofindan_inputpatternby assigningvaluestotheremaining inputs whichjustifiesthe value ofZ,wheremisthe numberoflinesinC.

a0 0 ^a _1b a2 b2 ^{ap- b-l}

Extra

r- ^Term

c0 p

S0 S1 s2 ^s

Fig.6. Gate-minimum p-bit paralleladder.

p-1

Lemma2:Suppose that the values 0, 1,D,and^Dareassignedon

allheadfan-out-points. Then the values of other nonhead fan-out- pointsaredetermined uniquely by the implication operation of time complexity o(m) provided thatnoinconsistency^occurs,wheremis the number of lines in^acircuit.

Theorem 10: Let Cbeacircuitwith khead fan-out-points. Then there is^analgorithm of time complexity 0(4k ^-m)tofind^atestfor

a_singlestuckfault in C, where^mis the number of lines in C. Proof:The^testgenerationforafaultonlineLcanbeperformed inthe followingsteps.

Step1:Fixa_{value ofL}to_{D(D) if}afault is stuck-at-0 (1) fault. Assignavalue 0,1,D,^orDtoeachhead fan-out-pointinCtodothe followingstepsfor each combination of valuesontheheadfan-out- points. Ifthereisnountried combinationremainingand^notesthas been found, then there existsnotestandsostop.

Step 2: Foreachassignment determine implications, that is, de- termine all the line values that^areimplied uniquely by the values assignedonthe headfan-out-points.Ifanyinconsistency^occurs,then

gobacktoStep 1.

Note that if^noinconsistency^occurs,the values of all(headand nonhead) fan-out-points are determined uniquely. (See Lemma 2.)Step3:for each fan-out-free subcircuit_Citowhoseoutputa_value

is assigned, findaninput assignmenttojustifytheoutputvalue of_Ci by usingthealgorithmofLemma 1. If thejustification fails,thengo

backtoStep 1.

Step4: Check whether ornoteveryD-path starts atthe line L undertest.Ifnot,gobacktoStep 1.

Step5: Check whetherornotthere isatleastoneD-path ending ata_{primaryoutput.Ifnot}and if there exists^nofan-out-free subcir- cuittowhoseoutput^novalue isassignedyet,thengobacktoStep1. Otherwise,for each fan-out-free subcircuitCi towhoseoutput^no value isassigned,findaninput assignmenttopropagateeither D^or

D _{to theoutputofCi} by using the algorithmofLemma 1. Ifthe propagationfails foreverysubcircuit,thengobacktoStep 1.Oth- erwise,wehave founda_test,andsostop.

The above algorithm requires the enumeration of at most 4k combinations of valueson_headfan-out-points. ByLemma 1,we see

thatSteps3and 5canbeperformedintime0(mi),wheremiis the number of lines inasubcircuit _Ci. ByLemma2,^{we see}thatStep2

canbe performedin time0(m). Hence,the abovealgorithmcanbe

carriedoutin0(4k * m)time. Q.E.D.

Thealgorithmshown in theproofofTheorem 10generatesall the combinations of values0, 1, D,^Donallheadfan-out-points, i.e.,4k .assignmentsfrom thebeginning.Wecanimprovethisby^animplicit enumerationtechnique. Ingenerating^atest,thealgorithmcreates adecisiontreein which^achoice is madeateachdecisionnodeonthe value ofalineoutofa_{number ofpossible}values. The initial choice isarbitrary,but itmaybenecessaryduring theexecution of the al- gorithm to return tothesame node and consider anotherpossible choice. This is called abacktrack. In order to guaranteethe time complexity 0(4k m),^wehavetomakesurethat backtracks^occur onlyatkheadfan-out-points.

Wethushaveshownthatthereexistsanalgorithm of timecom-

plexity 0(4k^-m)tofindatestforagivenfault ofa_circuit.Wecan

easilyextend the resulttoaclass ofk-head-fan-out-bounded circuits

asin thefollowingtheorem.

Theorem ^11: LetC be ^ak-head-fan-out-boundedcircuit. Then

x1 x2

X

40-

M-

there is analgorithmof timecomplexityO(16k^-m)to find a test for asingle stuck fault in C, where m is the number of lines in C.

Proof:Theproofis similar to thatofTheorem 11 in [23]. From Theorem 11 we have the following corollary.

Corollary1: Let Cbe ak-head-fan-out-boundedcircuit such that k =

_log2p(m)

for some polynomialp(m),where m is the number of lines in C. Then thefault detection problemforC issolvablein time complexity O(p(m)4 * m).

For ak-head-fan-out-boundedcircuit, inordertosolve the fault detection problem inpolynomialtime, itissufficient that k⁼ log p(m) for some polynomial p(m).

Theorems 10 and 11 indicate that thecomplexityordifficulty^of faultdetection is related to the number ofheadfan-out-pointsin the circuit.However, if there is no reconvergentpath,atest canbe found intime0(m)eventhough thereexistfan-out-points^{in the}circuit. This implies that it issufficienttoconsideronly reconvergent fan-out- points in order to get a similar result to Theorems 10 and 11. To further improvethetimecomplexity^wedefineamoregeneralsetS ofpoints whichsatisfiesthe_followingcondition.

Condition 1: For any reconvergent

fan-out-pointp,

either p

belongs

to S or any pathfromeachprimaryinputtop containsatleastone pointin S.

Obviously, the set of all head-fan-out-points satisfiesCondition 1. In order to find the smallest set that satisfies Condition 1, we first construct adirected graphG=(

_V,

E)suchthat V is thesetofvertices composed of allfan-out-pointsplustwo new vertices, a source s and asinkt, andEis the set of arcs such that

1) (s,h) E E for all headfan-out-pointsh,

2) (r, t) ^{E E}forall reconvergent

fan-out-points

r, and

3) (v, u) E E, v,u # s, tifthere isapathfromv to u inthe original circuitwithoutencounteringother

fan-out-points.

For this graph G, we caneasilyseethat a set Sof pointssatisfying Condition1 correspondsto a setof vertices whichcuts sandt.Hence, theproblem offinding^thesmallestsetS

_satisfying

Condition1 can be reducedto theproblem offindingthe minimumvertexcutset. ADesignfor Testability

Intheabove discussionwehave shown that the complexity of fault detectionis closely related to the number ofreconvergentfan-out- pointsin the circuit.Therefore,if wecan reduce the number of rec- onvergentfan-out-points, findinga test becomes easier. The reduction of thenumberofreconvergentfan-out-pointscan be done by placing inreconvergent paths anadditional Exclusive-OR gateasshownin Fig.7. Bycontrollingthevalue of x, we can always set an arbitrary valuetolineb,andobservethe valueofline a.Therefore,placing an Exclusive-ORgate on a line L is equivalent to cutting L logically. The totalnumberofadditionalinputs and outputs can be reduced to two ifwe use a scan shift register approach such as LSSD[10].

V. CONCLUSION

In this correspondencewe haveshown that the fault detection problem andtheirredundancy problemarebothNP-complete^even with a stringent condition such asmonotonicity andunatenessof circuits. Itis shown that for k-level (k^>3)

monotone/unate

circuits these problems areNP-completealthough thesecan be solved in polynomial timefor 2-level

monotone/unate

circuits. This

implies

that

by using

2-level

monotone/unate

circuitsit is

possible

to convert any circuitintoanequivalent easilytestablecircuit. Wehave also presentedanimplementation ofaneasily testable^PLA.

We have introducedaclass of circuits solvableinpolynomial

time,

called

k-head-fan-out-bounded

circuits. IfKis bounded

by log2p(m)

forsome_polynomialp(m), wherem isthenumberoflinesinacircuit, then the fault detection

problem

issolvableintime

O(p(m)4

^-

m).

Paralleladders, decoder circuits, linear circuits, etc., belong to this class. We have alsopresenteda moregeneral classbyconsidering reconvergentfan-out-points. A design approach isthenpresentedin

Fig.^7.

Reconvergent path.

which anarbitrary given circuit is converted to such aneasilytestable circuit by placing Exclusive OR gates in reconvergent paths.

Thealgorithm presented in the proof of Theorem IO is not efficient since it considers all the combinations of values0,1,D, D at all head fan-out-points in a circuit.However,since theobjectivesof this cor- respondence are toclarify the computational complexity offault detection problems, to present some classes of circuits for which a test canbe found in polynomial time, and to give an approach to the design fortestability,wehave not tried todevelopmoreefficient algorithms inthiscorrespondence.Betterand moreefficientalgorithmsfor test generationare nowbeingdevelopedin our group.

REFERENCES

[1] J.P.Roth, "Diagnosis of automata failures:Acalculusandamethod," IBMJ. Res.Develop., vol. 10, pp. 278-291, July1966.

[2[ P. Goel, "An implicit enumeration algorithm togeneratetests for combinational logiccircuits,"IEEE Trans. Comput., vol.C-30, pp. 215-222,Mar.1981.

[3] M. A.Breur andA.D.Friedman,Diagnosis and Reliable Design of Digital Systems. Woodland Hills, CA: Computer Science Press, 1976.

[4] P. H. Ibarra and S. K. Sahni,"Polynomiallycomplete fault detection problems," IEEE Trans. Comput., vol. C-24, pp. 242-249, Mar. 1975.

[5] M.R.Garey andD.S. Johnson, Computers andIntractability: A Guide tothe TheoryofNP-Completeness. San Francisco, CA: Freeman, 1979.

[6] M.J. Y.Williamsand J. B. Angell,"Enhancingtestability of large-scale integrated circuits viatestpoints and additional logic,"IEEETrans. Comput., vol. C-22, pp. 46-60, Jan. 1973.

[7] J.P.Hayes, "Onmodifying logicnetworks toimprove their diagnosa- bility,"IEEE Trans.Comput.,vol.C-23,pp.56-62,Jan. 1974. [8] K.K.Salujaand S.M.Reddy"Onminimally testable logic networks,"

IEEETrans.Comput., vol.C-23,pp.552-554, May1974.

[9] A.Vogeland W.Coy,"Improvingtestabilitybysimple modifications ofcombinational nets," Berichte derAbteilung Inform. der Univ. Dortmund, NR. 54, 1978.

[10] T. W.Williams andK. P.Parker,"Testing logicnetworksanddesigning fortestability,"Computer, pp.9-21andreferences,Oct.1979. [11] S.J.HongandD.L.Ostapko,"FITPLA:Aprogrammablelogic array

forfunctionindependent testing,"inProc._{FTCS, vol.10, Oct. 1980,} pp.131-136.

[12] H.Fujiwara,and K.Kinoshita,"Adesignofprogrammablelogicarrays withuniversal tests," IEEETrans.Comput., vol.C-30, pp. 823-828,

Nov.1981.

[13] M.A.Breuer, "Generation of faulttestsfor linear logic networks,"IEEE Trans.Comput.,vol.C-21, pp. 79-83,Jan.1972.

[14] S. C. Seth andK.L.Kodandapani,"Diagnosis of faults in lineartree networks,"IEEE Trans.Comput., vol.C-26, pp. 29-33, Jan. 1977. [15] R.Betancourt, "Derivation of minimumtest setsforunatelogical cir-

cuits,"IEEETrans.Comput., vol.C-20,pp.1264-1269,Nov.1971. [16] R.Dandapani,"Derivation of minimaltest setsfor monotonic logic

circuits,"IEEETrans.Comput., vol. C-22, pp. 657-661, July 1973. [17] S. B.Akers, Jr., "Universaltest setsfor logic networks,"IEEE Trans.

Comput.,vol.C-22,pp.835-839,Sept.1973.

[18] S. M.Reddy, "Completetest setsfor logicfunctions,"IEEETrans. Comput.,vol._C-22,pp.1016-1020,Nov. 1973.

[19] H.Fujiwara,"On closedness andtest_{complexityof logic}circuits,"IEEE Trans.Comput.,vol.C-30,pp.556-562,Aug. 1981.

c-31, 6,

[20] S. A. Cook, "The complexity of theorem proving procedures," in Proc. 3rd ACM Symp. Theory of Comput., 1971,pp. 151-158.

[21] A. V. Aho,J. E. Hopcroft, and J. D. Ullman, The Design and Analysis ofComputerAlgorithms. Reading, MA: Addison-Wesley, 1974. [22] H.C. Lai and S.-Muroga, "Minimum parallel binaryadders withNOR

(NAND)gates," IEEE Trans. Comput., vol. C-28, pp. 648-659, Sept. 1979.

[23] H.Fujiwara andS. Toida,"The complexityoffaultdetectionproblems for combinationallogic circuits," Dep. Syst. Design, Univ.ofWaterloo, Waterloo, Ont.,Canada, Tech. Rep. 78-P-HW-150681, June 1981.

In this correspondence we define a model of a memory which is subject to a very general class of failure modes. The model can be used torepresentsingle-cell, row, column, and entire chip failures. In ad- dition, the model can be used to represent higher levels failures(such as row orcolumn of chips on an array card) or other partial chip failures (such ashalf-chip). We derive a general equation for the reliability of the memory. All of the above referenced results are special cases of this equation.

TheReliability of Memory with Single-Error Correction W. F. MIKHAIL, R. W. BARTOLDUS, AND

R. A. RUTLEDGE

Abstract-This correspondence contains the derivation of the reliability, asa function oftime,of semiconductor memory with single-error correction. The results are applicable to a wide range of memory organizations.

It is well known that memory chip failures may affect a single cell, a row or column ofcells, or the entire chip. The memory model in this correspondence will simultaneously account for all these failure modes, as well as higher level failuremodes,such asthe loss of a row or column of chips,orof an entire bit- plane.

A newmeasureof memory systemreliabilityis proposed: the effective un- correctable error rate. This is definedasthe average rate of occurrence of uncorrectable errors over the time interval (0, T).

Index Terms-Error-correcting codes, fault-tolerant systems, memory reliability, semiconductiormemory,single-errorcorrection.

INTRODUCTION

The reliability of semiconductor memory with single-error cor- rection has been addressed in a numberofrecent papers[1]- [7]. In eachof these papers certain memorychip failuremodesareneglected. Inthiscorrespondencewegiveamethod for computing reliability which simultaneously accounts for these and for other failure modes.

Consideramemory which containsNwords ofWbitseach,and which iscapable of correcting a single-biterrorin any word. Ifeach cellfailswithprobability(1^-p) independently ofall othercells, then thereliabilityof the memory iseasilyseen tobe

[pW+

W(1

-p)pW1]N.

ThisequationisusedbyHilberg[7]andby Cox and Carroll[1], [2], althoughinadifferentform. It isknown, however,that memory cells donotfailindependently.Anarraychipwhichconsists ofarectan- gulararray of cells may fail inanumberofdifferent ways,including single-cell,row orcolumnofcells,and entirechipfailure[3], [4], [6], [8], [9].If anyoneofthesefailuremodes isassumedtobetheonly failuremode, then thecalculation ofreliabilityis stillsimple.Itis necessary onlytolet(1^-p) represent theprobabilityofab-cell failure,andreplaceNbyN/b in the aboveformula,^whereb is the numberof cellsaffected byeach failure. This is donebyLevine and Meyers [3]^andbyFerris-Prabhu [6]for thecasewhere every failure isachip-kill. SiewiorekandElkind [4]^usethisformula fourtimes, assumingthat eachofthe four modes inturnis theonly^{mode. The} calculationbecomesmore_complexwhen_multiplefailuremodesare considered simultaneously. Wangand Lovelace

[5]

consider four failuremodes:cell, half-column, column,andchip.Thisrepresents aconsiderableadvanceovertheother

models,

butit stilldoesnot accountfor the fact that bothrowsandcolumns of cells may fail.

ManuscriptreceivedJanuary5, 1981; revisedSeptember20,^1981. The authorsarewithIBMCorporation, Poughkeepsie,NY 12602.

THEMEMORYMODEL

Wefirst describe the abstract logical model of memory, and then show how thisgeneral model can accommodate a variety of specific casesby proper choice of the logical-to-physical mapping.

The memory is modeled logically as W bit-planes, where W is the number of bits per data word. Each bit-plane is an L-level hierarchy composed of arrays of arrays of arrays, etc., down to the lowest level. Alevel-i array is an_MiX

Ni

arrayof level-(i -1) arrays; i=2, 3,

* ,L. Alevel-I array is the smallest part of the memory which can fail, usually, but not necessarily, a single cell. It is assumed to be a 1 X 1 array: M1 =N1 = 1.A level-2 array is an M2 X N2 array of level-Iarrays; a level-3 array is an M3 X N3 array of level-2 arrays, etc.The entirebit-plane is a level-L array. We will refer to such a memory as an L-level memory. Fig.1 shows the structure of a typical three-level memory.

There are threefailure modes associated with each level-i array

(i

⁼ 1, 2, _A,

_L):

fai:

i, 2

Array

^{fail: Affectseverycellon onelevel-iarray} i,2 Rowfail: Affects every cell^{on one rowofonelevel-i}array

(i> 1)

i, 3 Column fail: Affects every cellononecolumn of one level-i array(i> 1).

There is one additional failure mode corresponding to failures (such as in the error correction logic) which would disable the entire memory. We refer to this asmode(0, 0)tobeconsistent with the above notation:

0, 0 Memoryfail Affects every cell in the memory. Areliabilityfunction is associated with each failuremode

Pi>(t) ^=Prob [failure^mode(i, j)^doesnotoccurbefore timet]. This probability applies independently ^toeach instance of failure mode(i,j).Forexample,eachrow oneach level-2 array hasproba- bility P22(t)ofsurvivinguntil time t,independentlyof all other such rowsand all otherfailure models.In alevel-Iarray, the threefailure modes(1, 1), (1, 2),and(1,3)^areequivalentbecauseM1 ⁼N1 ⁼ 1. Therefore,without lossofgenerality,weassumethat modes(1, 2) and(1, 3)cannot occur

The

_logical

_memorymodel isdetermined

_by

its structuralparame- ters

W,

L,(Mi, _Nj)i

=1,2,- ^,L and its component reliabilities

Pjj(t)-

^{i= 1,2,---L}

^j=

^1,2,3

Poo(t).

Inordertoapply the model to a particular memory, we also need thelogical-to-physicalmapping. Wemustspecify, foreach i, what physical entityisrepresentedby the level-i array. In general, more thanonemapping ispossiblefor any given memory system. A map-

P12(t) ⁼P13(t) ⁼ 1 forallt.

0018-9340/82/0600-0560$00.75

© 1982 IEEE

560